はじめに
科学・技術計算では, 一階微分を含まない二階の常微分方程式,
$ \frac{d^2 y}{d x^2} + k^2(x)y=S(x) {\tag 1} $
がしばしば出てくる(一次元シュレディンガー方程式など)。
この方程式の解法として,ヌメロフ法と呼ばれる非常に簡単かつ効率的な陽解法のアルゴリズがある。この方法は4次のルンゲ・クッタ法[1]よりも1次だけ精度が高い[2]。
本稿ではPythonを用いて簡単な例題を解く。
ヌメロフ法
一様な格子間隔 を
$h = x_{n}-x_{n+1} {\tag 2}$
として,ヌメロフ法による解法は
$y_{n+1}= \frac{(1-5bh^2)y_n-(1+\frac{1}{2}k^2_{n-1} h^2)y_{n-1}+b(S_{n+1}+10S_n+S_{n-1})}{1+bk^2_{n+1}h^2} + \mathcal{O(h^6)}{\tag 3} $
となる[1]。特に,$S(x)=0$のときは,1次元のヘルムホルツ方程式となり,ヌメロフ法による解は
$y_{n+1}= \frac{(1-5bh^2)y_n-(1+\frac{1}{2}k^2_{n-1} h^2)y_{n-1}}{1+bk^2_{n+1}h^2} + \mathcal{O(h^6)}{\tag 4} $
となる。
例題
$ \frac{d^2 y}{d x^2} = -4 \pi y, y(0)=1, y'(0)=0 {\tag 5} $
をx=0から1まで解く。
厳密解は
$ y = cos(2\sqrt \pi x){\tag 6} $
である。
ヌメロフ法では,$y[0]$に加えて$y[1]$の値が必要となる。
ここでは$y'(0)$の前進差分表現から,
$y'(0) = (y[1]-y[0])/h = 0 $として, $y[1] =1$とする。
また,$h = x_{n}-x_{n+1} = 0.005$とする
コード
"""
ヌメロフ法による2階常微分方程式の解法
"""
import numpy as np
import matplotlib.pyplot as plt
delta_x=0.005
xL0, xR0 =0, 1
Nx = int((xR0-xL0)/delta_x)
k2=np.zeros([Nx+1])
k2[:] = 4*np.pi
y=np.zeros([Nx])
# 初期条件
y[0] = 1
y[1]=1 # y'(0) = (y[1]-y[0])/delta_xと前進差分して評価
def Numerov (N,delta_x,k2,u): # ヌメロフ法による発展
b = (delta_x**2)/12.0
for i in range(1,N-1):
u[i+1] = (2*u[i]*(1-5*b*k2[i])-(1+b*k2[i-1])*u[i-1])/(1+b*k2[i+1])
Numerov(Nx, delta_x, k2, y) # ヌメロフ法による解
# for plot
X= np.linspace(xL0,xR0, Nx)
y_exact = np.cos(2*np.sqrt(np.pi)*X)
plt.plot(X, y,'o',markersize=2,label='Numerov')
plt.plot(X, y_exact,'-',color='red',markersize=0.5,label='Exact')
plt.legend(loc='upper right')
plt.xlabel('X') # x軸のラベル
plt.ylabel('Y') # y軸のラベル
plt.show()
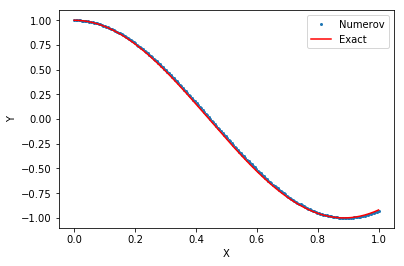
結果
点がヌメロフ法による数値解,赤線が厳密解をあらわす。
参考文献
[1] Qiita記事[Pythonによる科学・技術計算]4次のルンゲ-クッタ法による1次元ニュートン方程式の解法
[2] 阿部正典 ほか(訳),『クーニン 計算機物理学』