はじめに
Pythonを利用して,与えられたポテンシャル$V(x)$に対する時間に依存しない一次元シュレディンガー方程式
$\frac{d^2}{d x^2}\psi(x) +k^2(x) \psi =0 {\tag 1}$
$k^2(x) = \frac{2m}{\hbar^2}(E- V(x)) {\tag 2}$
を射撃法[補遺]とよばれる数値計算法によって解き,波動関数とエネルギー固有値を求める。
本稿では**同分野の典型的な問題である井戸型ポテンシャルを考える。微分方程式の解法はヌメロフ法[1]**を用いる。
射撃法は従来から使われる方法で,常微分方程式の境界値問題を初期値問題として解く方法であり,古くから使われている。
射撃法を用いたPythonコードはネットでなかなか見つからない(2017年9月4日現在)。本記事が読者の量子力学の理解を深めることに少しでも貢献できれば幸いである。
コード内容: 深い井戸型ポテンシャル
コードはすべてRydberg原子単位を用いる。
これは,
電子の質量$m=1/2$
ディラック定数$\hbar =1$
長さをボーア$a_{B}=(0.529177 Å)$単位,
エネルギーを$1Ry=13.6058 eV = $
とするものである。
束縛状態の波動関数とエネルギー固有値を求める。探索するエネルギーは E = 0-20 (Ry)とする。
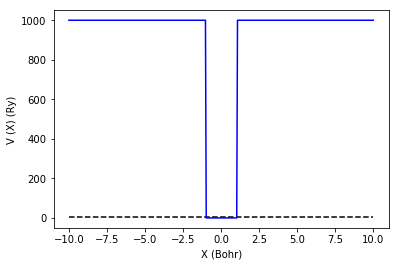
図1. 井戸型ポテンシャル。井戸の幅は2 Bohr, 井戸の高さは1000 Ryである。
無限に深い井戸の場合,エネルギー固有値の厳密解は
$E_n = n^2 \pi^2/4 {\tag 2}$
であり,
E1=2.46740110027234 (Ry)
E2 = 9.869604401089358 (Ry)
E3 = 22.20660990245106 (Ry)
...
となる[1]。
コード: 深い井戸型ポテンシャル
テスト計算のため,比較的ゆるやかな計算条件にしている。精度を向上させる場合は,
グリッド幅 delta_xを減らすと良い。
"""
射撃法+ヌメロフ法による時間に依存しない一次元シュレディンガー方程式の解法
深い井戸型ポテンシャル
1 Sept. 2017
"""
import numpy as np
import matplotlib.pyplot as plt
delta_x=0.05
xa =1 # 井戸の境界。 x=±xaに井戸の端がある。
eps_E=0.005 # 収束条件
nn=5 #両端から積分を行う際の両端の座標をxa(と-xa0)の何倍にするかを示すパラメータ
xL0, xR0 = -nn*xa, nn*xa
Nx = int((xR0-xL0)/delta_x)
delta_x = (xR0-xL0)/(Nx)
i_match = int((xa-xL0)/delta_x) #uLとuRの一致具合をチェックする位置のインデックス。井戸の境界に選んでいる。
nL = i_match
nR = Nx-nL
print(xL0,xR0, i_match, delta_x)
print(nL,nR)
uL = np.zeros([nL],float)
uR = np.zeros([nR],float)
E=np.pi**2/4
print("E= ",E)
print("xL0,xR0, i_match, delta_x=",xL0,xR0, i_match, delta_x)
print("Nx, nL,nR=",Nx, nL,nR)
def V(x): # 井戸型ポテンシャルの設定
if np.abs(x) > xa :
v = 1000.0
else :
v = 0
return v
# 境界条件・初期条件セット
def set_condition():
uL[0] = 0
uL[1] =1e-6
uR[0] = 0
uR[1] =1e-6
#
set_condition()
def setk2 (E): # for E<0
for i in range(Nx+1):
xxL = xL0 + i*delta_x
xxR = xR0 - i*delta_x
k2L[i] = E-V(xxL)
k2R[i] = E-V(xxR)
def Numerov (N,delta_x,k2,u): # ヌメロフ法による発展
b = (delta_x**2)/12.0
for i in range(1,N-1):
u[i+1] = (2*u[i]*(1-5*b*k2[i])-(1+b*k2[i-1])*u[i-1])/(1+b*k2[i+1])
xL=np.zeros([Nx])
xR=np.zeros([Nx])
for i in range (Nx):
xL[i] = xL0 + i*delta_x
xR[i] = xR0 - i*delta_x
k2L=np.zeros([Nx+1])
k2R=np.zeros([Nx+1])
setk2(E)
def E_eval():
uLdash = (uL[-1]-uL[-2])/delta_x
uRdash = (uR[-2]-uR[-1])/delta_x
logderi_L= uLdash/uL[-1]
logderi_R= uRdash/uR[-1]
return (logderi_L- logderi_R)/(logderi_L+logderi_R)
# ポテンシャル関数のプロット
XXX= np.linspace(xL0,xR0, Nx)
POT=np.zeros([Nx])
for i in range(Nx):
POT[i] = V(xL0 + i*delta_x)
plt.xlabel('X (Bohr)') # x軸のラベル
plt.ylabel('V (X) (Ry)') # y軸のラベル
plt.hlines([E], xL0,xR0, linestyles="dashed") #Energy
plt.plot(XXX,POT,'-',color='blue')
plt.show()
#
# k^2(x)のプロット
XXX= np.linspace(xL0,xR0, Nx+1)
plt.plot(XXX, k2L,'-')
plt.show()
#
def normarize_func(u):
factor = ((xR0-xL0)/Nx)*(np.sum(u[1:-2]**2))
return factor
def plot_eigenfunc(color_name):
uuu=np.concatenate([uL[0:nL-2],uR[::-1]],axis=0)
XX=np.linspace(xL0,xR0, len(uuu))
factor=np.sqrt(normarize_func(uuu))
plt.plot(XX,uuu/factor,'-',color=color_name,label='Psi')
plt.plot(XX,(uuu/factor)**2,'-',color='red',label='| Psi |^2')
plt.xlabel('X (Bohr)') # x軸のラベル
plt.ylabel('') # y軸のラベル
plt.legend(loc='upper right')
plt.show()
# 解の探索
# 境界条件1 (偶関数)
EEmin=0.1
EEmax = 20
delta_EE=0.01
NE = int((EEmax-EEmin)/delta_EE)
Elis=[]
Solved_Eigenvalu=[]
check_Elis= []
for i in range(NE+1):
EE=EEmin+i*(EEmax-EEmin)/NE
set_condition_even()
setk2(EE)
Numerov (nL,delta_x,k2L,uL)
Numerov (nR,delta_x,k2R,uR)
a1= E_eval()
if a1 :
Elis.append(EE)
check_Elis.append(a1)
if np.abs(a1) <= eps_E : #解を見つけた場合のプロット
print("Eigen_value = ", EE)
Solved_Eigenvalu.append(EE)
plot_eigenfunc("blue")
plt.plot(Elis, check_Elis, 'o',markersize=3, color='blue',linewidth=1)
plt.grid(True) #グラフの枠を作成
plt.xlim(EEmin, EEmax) # 描くxの範囲を[xmin,xmax]にする
plt.ylim(-10, 10) # 描くyの範囲を[ymin,ymax]にする
plt.hlines([0], EEmin,EEmax, linestyles="dashed") # y=y1とy2に破線を描く
plt.xlabel('Energy (Ry)') # x軸のラベル
plt.ylabel('Delta_E_function') # y軸のラベル
plt.show()
# 境界条件2 (奇関数)
EEmin=0.1
EEmax = 20
delta_EE=0.01
NE = int((EEmax-EEmin)/delta_EE)
Elis=[]
Solved_Eigenvalu=[]
check_Elis= []
for i in range(NE+1):
EE=EEmin+i*(EEmax-EEmin)/NE
nL = i_match
nR = Nx-nL
uL = np.zeros([nL],float)
uR = np.zeros([nR],float)
set_condition_odd()
setk2(EE)
Numerov (nL,delta_x,k2L,uL)
Numerov (nR,delta_x,k2R,uR)
a1= E_eval()
#print ("a1=",a1)
if a1 : # a1がTrueのとき
Elis.append(EE)
check_Elis.append(a1)
if np.abs(a1) <= eps_E :
print("Eigen_value = ", EE)
Solved_Eigenvalu.append(EE)
plot_eigenfunc("blue")
plt.plot(Elis, check_Elis, 'o',markersize=3, color='red',linewidth=1)
plt.grid(True) #グラフの枠を作成
plt.xlim(EEmin, EEmax) # 描くxの範囲を[xmin,xmax]にする
plt.ylim(-10, 10) # 描くyの範囲を[ymin,ymax]にする
plt.hlines([0], EEmin,EEmax, linestyles="dashed") # y=y1とy2に破線を描く
plt.xlabel('Energy (Ry)') # x軸のラベル
plt.ylabel('Delta_E_function') # y軸のラベル
plt.show()
結果(1)
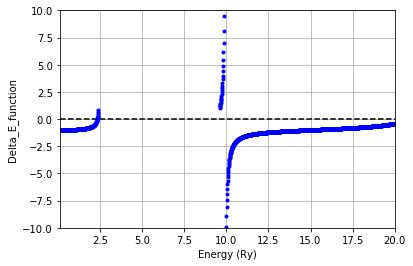
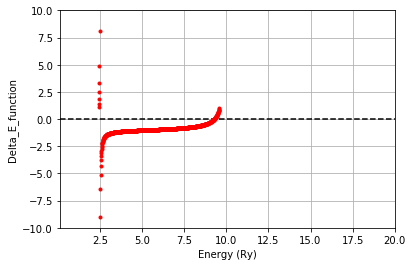
(1-A) 評価関数の計算
(1-B)得られた波動関数と固有エネルギー
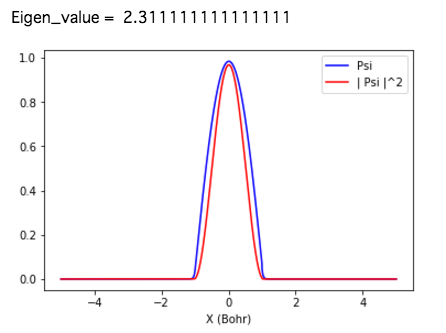
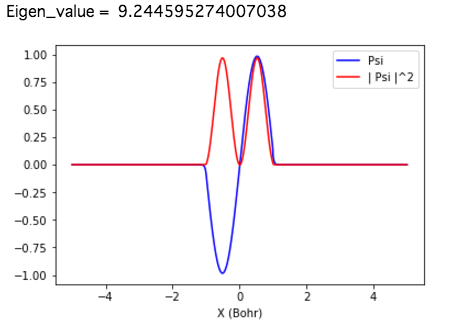
図. 基底状態の波動関数$\psi(x)$および確率密度$|\psi(x)|^2$
厳密解
$E_1=2.4674011$と比べ4%程度の誤差で一致している。
厳密解と比べ6%以内で一致している。
$E_2 = 9.8696044$ (Ry)
補遺: 射撃法 (シューティング法)
(1)はじめに
1次元シュレディンガー方程式
$\frac{d^2}{d x^2}\psi(x) +k^2(x) \psi =0 {\tag 1}$
$k^2(x) = \frac{2m}{\hbar^2}(E- V(x)) {\tag 2}$
は,束縛状態では
$\lim_{x \to \infty} \psi(x) = 0 {\tag 3}$
を満たす。
これが境界条件である。上記式(1,2)を境界条件(3)の下で解く。そのとき,任意の$E$に対して解が存在するとは限らない。ある特定の$E = E_n$のときにのみ解が存在する。それを固有値という。そしてそのときの関数は固有関数と呼ばれる。
すなわち,式(1)は固有方程式と呼ばれる数学的問題に帰着する。それを**"固有値問題"**といったりする。
(2)射撃法の手順
射撃法は微分方程式の固有値問題の解法の一つである。
境界条件を満たした関数を考え,両端から積分常微分方程式を初期値問題として積分していき,ある地点で両者の解が一致するのかを調べる。もし正しいエネルギー固有値を与えていると,両者の解は一致するであろう。
この性質を利用したものが射撃法である[2]。以下の手順を行い固有値問題を解く。
1.エネルギー固有値の推定値を与えて微分方程式を両端から解く
2.適当な地点で両者の解関数が一致するか調べる
3-1.一致しない場合(図1)は推定エネルギー固有値を変えて1に戻る
3-2.一致する場合(図2) はエネルギー固有値と固有関数を得たことになる。
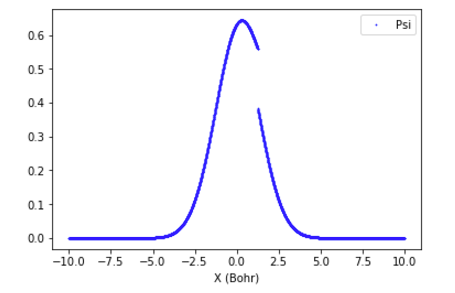
図1: 左側と右側から微分方程式を解いて得られた2つの波動関数。解が滑らかに接続されていない (3-1に対応する)。
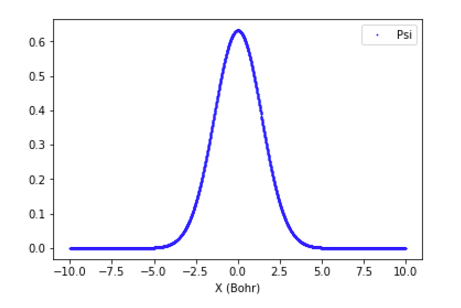
図2: 解が滑らかに接続している場合。このときに与えたエネルギーと得られた波動関数は,正しい固有値および固有関数である。
補遺: 解の評価法
これについては,前後してしまったが,
[Pythonによる科学・技術計算] 定常状態の一次元シュレディンガー方程式の射撃法による解法(2),調和振動子ポテンシャル,量子力学
を参考にしていただきたい。
参考文献
[1] Qiita記事 [Pythonによる科学・技術計算]ヌメロフ法による2階常微分方程式の解法,数値計算