[Pythonによる科学・技術計算] 3次スプライン補間，scipy

scipy.interpolateのinterp1dメソッドを利用して3次スプライン補間を行う。

内容

例題:$y=1/(1+x^2)$を考える。11点のデータセット$(x_i, y_i)$をサンプルし，補間する。
この関数は，ラグランジュ補間ではうまくいかない(Qiita記事を参照)。

from scipy.interpolate import interp1d
import numpy as np
import matplotlib.pyplot as plt

x =np.linspace(-5,5,num=11)
y = 1.0/(1.0+x**2)
f_line = interp1d(x, y)
f_CS = interp1d(x, y, kind='cubic')  #3次スプライン補間実行！

# for plot

xnew =np.linspace(-5,5,num=51)
plt.plot(x, y, 'o',   xnew, f_CS(xnew), '-')
plt.legend(['Raw data','Lagrange', 'Cubic spline'], loc='best')
plt.xlim([-6, 6])
plt.ylim([0, 1.4])
plt.show()

結果

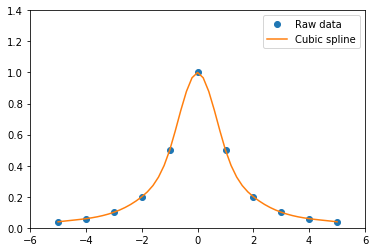
青印がサンプルした11個のデータ点。オレンジ線がスプライン補間したもの。

[補遺]

以下の図で示されるように，ラグランジュ補間ではこの関数をうまく補間できない。

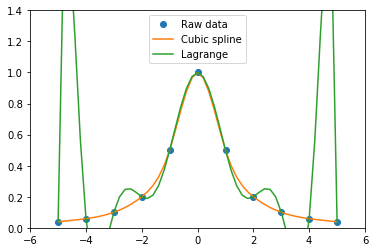
青印がサンプルした11個のデータ点。オレンジ線がスプライン補間，緑線がラグランジュ補間したもので，両端近傍で不自然な振動を起こす。