はじめに
scipyのinterpolateのlagrangeメソッドを用いた補間を行う。
与えられたN+1個のデータセット ($x_i$, $y_i$) (i=0,2, 3, ... , N)をN次多項式により補間(ラグランジュ補間)するプログラムをPython3で実装する。
例として$y=1/(1+x^2)$を考える。11点のデータセット($x_i$, $y_i$)をサンプルし,それを10次多項式で内挿する。この関数はラグランジュ補間がうまくいかないRunge現象を起こす例として知られている。
内容
コード1: scipy・numpyを利用。最小のコード(急いでいる人はこちら)
コード2: 補間のための係数をコード中で計算。手法の勉強をするならこちら。
計算コード(1): scipy・numpyを利用
from scipy.interpolate import lagrange
import numpy as np
import matplotlib.pyplot as plt
## メイン
x =np.linspace(-5,5,num=11) #[-5,5]の範囲を11等分して xに格納
y = 1.0/(1.0+x**2) #本例題で考えている関数である y = 1/(1+x^2)を定義
f_Lag=lagrange(x,y) #scipy.interpolate.lagrangeによるラグランジュ補間実行
##
# for plot
xnew =np.linspace(-5,5,num=51) # [-5,5]の範囲を51等分して xnewに格納
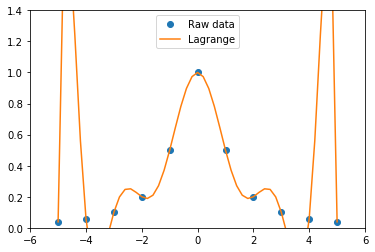
plt.plot(x, y, 'o', xnew, f_Lag(xnew), '-') # 生データを"o"で, ラグランジュ補間したものを線('-')で描く。
plt.legend(['Raw data','Lagrange'], loc='best') # legendの指定
plt.xlim([-6, 6]) # x軸のプロット範囲
plt.ylim([0, 1.4]) # y軸のプロット範囲
plt.show()
結果(1)
青印がサンプルした11個のデータ点。オレンジ線がラグランジュ補間したもの。
計算コード(2) 補間のための係数をpythonで計算
"""
補間: ラグランジュ補間
例題: y = 1/(1+x**2): を区間 -5から5まで11点サンプリングし,それをラグランジュ補間する。
"""
from math import pi,e, log, factorial
import matplotlib.pyplot as plt
###
def g(i, x): # ラグランジュ補間の係数の計算。メイン。
dum=1.0
for j in range(len(x_lis)):
if j != i :
dum *= (x-x_lis[j])/(x_lis[i]-x_lis[j])
return dum
#
def fLag(x,m): #ラグランジュ補間
dum=0.0
for j in range(m):
dum += y_lis[j]*g(j, x)
return dum
###
## 例題のためのデータセット構築
m = 11 # x= -5 から5まで等間隔に11点サンプリング
x_lis = []
y_lis = []
def yy(x):
return 1/(1+x**2) # 例題の関数 y = 1/(1+x**2)
for k in range(m):
xm = -5.0 + 10.0*k / m
x_lis.append(xm)
y_lis.append(yy(xm))
plt.plot(x_lis,y_lis, 'o',label='Row data')
##
### ラグランジュ補間実行
mm = 5000
y_Laglis = []
xx_lis = []
for k in range(mm):
xm = -5.0 + 10.0*k / mm
xx_lis.append(xm)
y_lis_exact=[]
for j in range(mm):
y_Laglis.append(fLag(xx_lis[j],m))
y_lis_exact.append(yy(xx_lis[j]))
# plot
plt.grid(True)
plt.xlabel('x',fontsize=24)
plt.ylabel('f(x)',fontsize=24)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.plot(xx_lis,y_Laglis, color='Red',label='Lagrange')
plt.plot(xx_lis,y_lis_exact, color='Black',label='Exact')
plt.legend(loc='upper left')
plt.show()¥
結果(2)
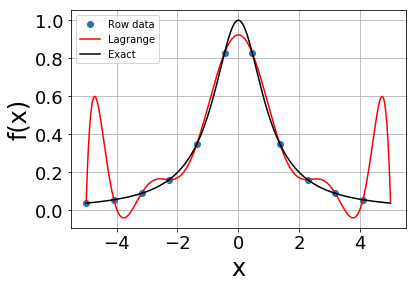
青印がサンプルした11個のデータ点。赤線がラグランジュ補間したもの。黒線は厳密解を表す。
次数(データ点)を増やしていくと,中央部分の近似は良くなるが,両端に近い部分の近似が悪くなる。次数を上げると誤差が大きくなり,ついには無限大に発散する例として知られている。これは等間隔分点を用いたためであり,分点の配位とを中央付近で荒く両端で細かくすると避けられることが知られている[1]。
補遺: 等間隔ラグランジュ補間が,点数を増すにしたがってもとの関数f(x)へ近づくための条件
区間[-1,1]の場合: $f(x)$の定義域を複素平面へ解析接続した際,その特異点$z$が
$|(1+z)^{1+z}| \leqq 4 e^{\pi |Im(z)|}$
を満たさないことである。
本例題でいえば, $f(z) = 1/(1+z^2)$の特異点zは$±i$であり,
不等式の右辺は $4e^\pi= 92.562770531... $,
左辺は$|(1+i)^{1+i}| = 0.644793...$
であるから, 上の不等式を満たしてしまっているため,等間隔分点を用いたラグランジュ補間(多項式補間)は分点数の増化とともに誤差が増加する。
なお,f(x)が区間[a,b]において連続な関数なら, 分点$x_n$を以下のように選べばNが無限大の極限で補間多項式がf(x)に近づく[2]。
$x_n = (a+b)/2 + (b-a)(sin(-\pi/2+n\pi/N))/2,$
$(n = 0, 1, 2, ...,N) $
また,直交多項式(たとえばチェビシフ多項式)の零点を分点に選ぶ多項式補間では上でみたようなRung現象は生じない[1]。
参考文献
[1]森正武, 「数値解析 第二版」, 共立出版, 2002.
[2]伊理正夫・藤野和建,「数値計算の常識」, 共立出版, 1985.