AHC001参加記(schwarzahl)
AtCoder Heuristic Contest 001 が 2021-03-06(土) 12:00 ~ 2021-03-14(日) 20:00、
つまり9日間開催されていて僕にはあまりにも長く
2日目にして既に「誰かに話したい・・・!」という気持ちが強まってしまったので
ルール違反にならないようmarkdownに書いて気持ちを発散することにしました
Codingame然りマラソン系は熱くなりやすく
僕自身、この手のコンテストに出るのが初めて、というわけではないのですが
twitter以外にちゃんと参加記を書こうと思ったのは
これが初めてかもしれません
初めてだから・・・と甘えるわけではないですが
多分、他の人がしっかり問題内容については解説するでしょうし
参加した人だけが読む気がするので、問題内容についてはこの記事では触れません
(後で良さそうな問題解説をしてくれてる人の記事へのリンクは貼るかもしれません)
あとがき(まとめ)
記事的には「はじめに」ですが最後に書いてるので「あとがき」です
AHC001お疲れ様でした!
コンテスト中の自己最高得点は48,435,227,971点でした。
seed0のビジュアライズはこんな感じです。
まだまだ詰めが甘いですが、これが自分の限界でした。
ほぼほぼ2日目に提出したところからほとんど変わってません。
アルゴリズムはざっくり言うとこんな感じです↓
-
1px * 1pxから始めて他の広告に衝突するまでスコアが低い順に1pxずつ拡大する - 他の広告を縮小してもスコアが大きくなるのであれば拡大する
- 全て終わった後のスコアを各広告に累積で乗算して最初からやり直し
- これを4.5秒経過するまで繰り返す
工夫したポイントは
- 優先順位付きキューを利用して1px拡大するたびに一番評価値が低い広告を選択する
- 広告の衝突判定は
10000 * 10000のbooleanを10000*10000/64のLong配列でBitとして扱って処理する - 各広告のスコアは簡易的に
min(希望面積, 現在の面積) / max(希望面積, 現在の面積)で扱う
あたりです。
他の広告を縮小してもスコアが大きくなるのであれば拡大する
この部分の処理がだいぶ雑で広告を左側へ拡大するときに
- 左側の広告の右側を縮小する
- 左側の広告を左にずらす
の二択しか用意できなくて実際は
- 左側の広告を上や下に縮小する/ずらす
- 右側の広告の上下を縮小してから左側へ拡大する
- 玉突きの要領で複数の広告をずらす
みたいな選択肢を用意できればもっとスコアが上がりそうでした(が、短い時間で処理できる実装ができませんでした)。
正直、ルールベースで実装する問題ではなかったんじゃないかなー、と思います。
おそらく上のようなことを考えなくても各広告が忖度して動いてくれるような
提案確率、遷移方法、採択確率を上手く設計して焼き鈍しに落とし込むのが最適だったんじゃないかなー、と。
途中、焼き鈍しの勉強をしてそちらに方針を切り替えようとしましたが
全然スコアが出るような実装をできませんでした。
今回、他の人の参加記を読んで方針の立て方や考え方を勉強したいですね!
以下、これまでに書いてきた走り書きメモレベルの文章です。
twitterに書く代わりに書いてたのでqiitaで読むに耐えない文章ですが
(そもそもtwitterですら読むに耐えないぼやきの可能性すらありますが)
もし興味がある方はライブ感を楽しむつもりで読んでもらえれば幸いです。
1日目(2021年3月6日)
正午(12時)開始
問題を読んで「とりあえず正の点が取れるな」と思ったので
何も考えずに全ての広告を1x1にしてsubmit、5位
始める前から「最終1位は無理でも瞬間的に1位を取りたい・・・!」と思っていたので
ここで1位を取ってしまいたかったのですが5位でした
30分制限があるのでここから30分は提出できません
ガチで瞬間1位を狙うならもう一歩だけ進めたコードを30分以内に作って提出すべきでした
30分後に急いで2回目を提出
とりあえずx座標順に並べて一つ隣の広告まで幅をとった
縦に長い広告を並べれば点数が上がるのでは、とやってみました
WAでした、よくよく考えればxが等しい広告が複数与えられることがあるので
その広告は幅が0になってしまいます
提出直前に気付いて「被るやつは全部(0,0,1,1)で投げとくかー」と
無理やり変換してしまったのですが、
共通部分が正の面積を持ってはならない
この制約に引っかかってWAになってしまいました
さらにその30分後に3回目の提出
晴れて瞬間3位をとることができました!
この手の問題は制限時間いっぱいランダムウォークさせるのが定番なので
この30分で必死に以下の方針で書きました
- 4.5秒間、ひたすら以下を繰り返す
- n個の広告からランダムに1個選び、面積がrより小さければ4方向からランダムに1方向選んで拡大する
- 拡大可能かのチェックは事前に10000x10000のboolean配列を用意して拡大するたびにtrueで値を埋めておき利用する
これだけで90点が取れるとは正直思っていませんでした
(1ケースの満点が10億点、50ケースあって合計が500億点、上記の提出で450億点取れたので100点満点で90点)
このあと4回ほぼ30分おきに提出をし、得点は徐々に上がるのですが
残念ながら他の人の伸びの方が早く順位を上げることはできませんでした・・・
4回目の提出はPriorityQueueを導入して面積/rの比が小さい順に拡大するように変更したようです
そして5回目の提出はPriorityQueueの評価値をより厳密にスコアに近づけるためmin(r, 面積)/max(r,面積)に変更したようです
なぜ推測みたいな書き方かというとこの辺でかなりコードがごちゃごちゃしてきてしまって
今コードを読んでも何をやっているかぱっと見でわからなくなってしまっているからです・・・
おそらく上に書いたこと以外にも色々やってるのでしょうが
これを読み解いていたら時間がもったいないのでここでは割愛します
6回目の提出時にはなるべく広告(Space)クラスに機能を寄せるリファクタリングをして読みやすくなっています
「3回目」と「4回目、5回目、6回目」の大きな違いは
開始時は乱択ではなく決まった方法でやっていることですね
評価値が低い順に4方向の面積を1ずつ広げていく、という操作は乱数に関係なく一定です
そしてその操作ができなくなったところで次のステップとして乱択をしているようです
ここは3回目と同じくn個の広告からランダムに1個選んで拡大しているのですが
面積がrより大きい場合に何もしないのではなく縮小してから拡大するように変更しています
これによって「ちょっと形が合ってない」みたいなところが多少乱数で吸収できるようになりました
3
4999 2499 50000000
2499 7499 25000000
7499 7499 25000000
確かこんなテストケースをローカルで用意して試した記憶があります
このテストケース、3回目や4回目の方針のままだと上の広告が下半分にはみ出して点数が上がらないのですが
縮小も挟むようにしたおかげできっちり満点が取れるようになりました
書き忘れていましたが縮小時にも10000x10000のboolean配列は更新しています
1ずつ大きくしたり小さくしたりする分には高々10000回以下のfor文に収まるのでそこまで計算量がかからないのがありがたいです
7回目の提出は10000x10000のboolean配列を10000x10000/64のlongによるBit配列に変更しました
実は本当に変更しただけでfor文は同じ回数まわしているのですが
それだけで速度が上がって乱択の回数が増えて微妙に点数が上がっています
8回目の提出は(ちょっと雑ですが)範囲に対して操作できるようにリファクタリングして
拡大/縮小時のtrueやfalseを立てる操作を64倍速にしました
とはいえこの変更はそこまで得点が上がりませんでした
もしかすると既に試行回数は十分で方針が良くないのかもしれません
ここまでずっとほぼ30分おきに提出しつつずっと頭を回しながらコードを書いていたので疲れてしまいました
一旦お昼寝をします
19時に更新されるApexのデイリーをこなして再開!
よくよく8回目の提出までの出力を見てみると
まだ四方に余裕があるのに面積がrより小さい広告がありました
これはランダムな方向に縮小したあとランダムな方向に拡大を試みていたため
縮小した方向側に余裕ができているパターンがあったようです
これをカバーするために4.5秒間乱択をした後の出力前に
「面積が足りないけれど拡大できる広告は拡大する」という処理を追加して
20時に9回目の提出をします
うーん、予想通りほとんど点数は上がりません
よく考えると「面積がrより小さい」からといって拡大したらスコアが上がるとは限りません
厳密に「スコアが上がるのであれば拡大する」という処理にすべきです
その部分を書き換えて22時に10回目の提出をします
点数が下がってしまいました、まぁ大した変更ではなく乱数の誤差の範囲だったのでしょう
毎回「左、上、右、下」の順番に拡大できるかチェックしていたのですが
もしかすると左へ拡大する前に上に拡大した方がスコアが高いパターンがあるかもしれません
そのチェックを入れて30分後に11回目の提出!
予想通り誤差の範疇でした
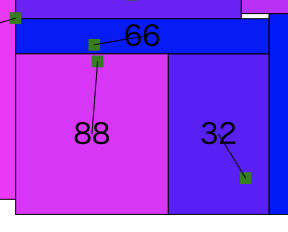
実はこの時あることに悩まされていました
それは「人間から見れば明らかに有利な方向に広告が拡大してくれない」ということです
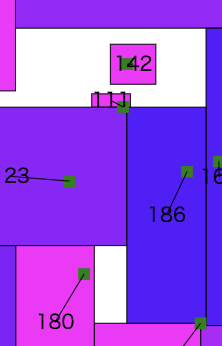
186番の広告は面積が明らかに足りていません
本来であれば上に伸ばせば良いのですが、111番と142番の広告が邪魔しています
しかしこの111番と142番の広告はxの座標が186より左にあります
つまり全体を左にずらせば186番の広告は上に伸びることができるのです
これは「人間から見れば明らかに有利」です
しかし今の自分のコードではこれをコードに組み込むことができません
縮小や拡大をランダムで繰り返し、その試行回数を稼げばなんとかなるのか・・・?
特に良い方針も思いつかないまま日付は2日目に変わります
2日目(2021年3月7日)
日付が変わって寝る準備をしていたら閃いてしまいました
「縮小してから拡大、ではなく"とりあえず拡大"して衝突してる広告は全部縮小しちゃえばいいのでは・・・?」
「その後の合計スコアを比較して悪くなっていれば不採用、良くなっていれば採用するだけで良さそう」
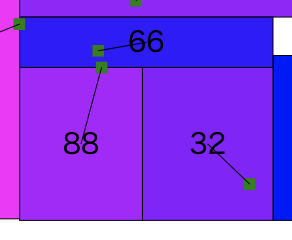
実はこの方法はさっきの図の状況を改善する一手にはならないのですが
(なぜかというと上方向に押す場合は下方向を縮小する、というシンプルな方法でないと試行回数を稼げないから
先ほどの方法は111のyが186と面していて下方向を縮小することができない
この図の場合は先に左へギリギリまでずらして初めて186が上方向に拡大することができる)
こういうタイプの状況を改善するには十分有効でした
というかさっきの図があまりにもコーナーケースで
こういう場面の方がよほどたくさんあったようです
上記の処理を乱択後の出力前に挟んで意気揚々と12回目の提出!
TLE・・・ 4.5秒の乱択を4.0秒に減らすだけでは
後処理の時間が足りなかったようです
さて、秒数を減らしてすぐに提出したいところですが30分制限がかかっています
ここであることに気が付きます
「そもそも乱択いらなくね?」
「最初からスコアが大きくなるように拡大していって邪魔なものは縮小させる上記の方針だけでいいのでは」
13回目の提出
見事、48億点台に乗せることができました!
ところで「試しに拡大させたときに衝突している他の広告を列挙する方法」は
このタイミングでは10000x10000のint配列を使っていました
初期値0、拡大時に拡大した辺をidで埋めて
縮小時には縮小した辺を0で埋める、という操作をしていました
そう、さっきまで利用していたlongによるBit配列は使えなくなってしまいました
(正確には「衝突するまで拡大する」部分は引き続きBit配列を使っていました
両方使うのも微妙かなー、と一度ここの部分を10000x10000のint配列を使うように変更したら
500msで終わる処理が2500msもかかってしまったのですぐにBit配列を使うように戻しました)
14回目の提出
例のごとく「左、上、右、下」の順番に拡大できるかチェックしていて
もしかしたら、と思って乱数を使って50%の確率で「上、右、下、左」の順番に拡大するよう変更したのですが誤差の範囲でした
深夜3時も回って流石に疲れてきました
ここで一度お布団に入ります
このタイミングでふとcolunさんの記事を思い出していました
というのもこのタイミングの僕の解法はまとめるとこんな感じになっていました
- 各広告を(x,y)に1x1で配置、longによるbit配列も同じ位置をtrueで埋める
- スコアが小さい順に四方へ1拡大する(できない場合はしない、面積がrより大きい時もしない)
- 拡大できるか否かは先述のlongによるbit配列でチェック、拡大時に拡大した辺をtrueで埋める
- スコアが小さい順に四方に拡大してみる、拡大して衝突する広告は縮小して辻褄を合わせる
- 合計スコアが下がるならば不採用、合計スコアが上がるならば採用
- 全広告について行ったらもう一度スコアが小さい順にソートして繰り返す
- 4.5秒経ったら繰り返さずに終了する
そう、結局のところ今は乱数が絡まない貪欲手法だったのです
マラソン系コンテストといえば焼き鈍し、という印象が強いですが
僕はどうしても焼き鈍しが苦手でいつも貪欲や山登りばかり書いてしまいます
そして今回も気付けば「乱数が絡まない貪欲」な処理しか書いていませんでした
焼き鈍しでは「状態の遷移」という言葉を使いますが、
日付が変わるタイミングで閃いた「試しに拡大して周りを縮小させる」、
これこそいわゆる「状態の遷移」なのでは・・・?
今は温度管理も何もなくただ「スコアが上がるとき」だけ採用している、
つまりただの山登りですが、ここでcolunさんの記事をしっかり読んで
焼き鈍しや温度管理を理解することでより一歩上に行けるのでは・・・?
(再掲)
それが先ほどのツイートの意図でした
きっと僕より順位が高い人はとっくにこの遷移を処理に組み込んでいて
既に焼き鈍しを試しているに違いない・・・!
そう思ったのでした
でも既に眠いです 深夜3時です
とてもcolunさんの記事を読める体力も精神力もありません
そのまま寝落ちしました
午前10時半、目が覚めました
「貪欲なら4.5秒制限いらなくない?」
TLEでした
4.5秒制限を入れればTLEしないことを確認します(あと得点が変わらないことも)
でもこれは先ほどの疑問の否定にはならない気がしました
「そもそも10000x10000のint配列なんか使ってるから重いのでは」
「拡大時に辺だけチェックできる方が軽いと思ったけど広告の数は高々200だし広告同士比較した方が早い?」
10000x10000のint配列を削除して関連する処理を全て等価に書き換える大幅なリファクタリングを行いました
TLEしませんでした
っていうか実行時間が1708msになりました
10000x10000のint配列なんていらんかったんや・・・!
int配列周りの関数めっちゃ作ったけど全部消しました
(消した、といってもgit管理してるのでいつでも戻せるんですが)
さて、これで3秒近く余裕ができました
いわばここまでは前処理、2秒以内に48億点を稼ぐ方法は見つかったわけです
あとは3秒で可能な限り点数を上げていくのが今後の課題になりそうです!
ここまでは2日目に一気に書き上げました
ここからはリアルタイムで今の思考を整理しながら書いていきます
そういえばこの時点で入れていたアルゴリズムを書き忘れていたことに後から気付きました
- スコアが小さい順に四方に拡大してみる、拡大して衝突する広告は縮小して辻褄を合わせる
- 合計スコアが下がるならば不採用、合計スコアが上がるならば採用
この部分について、衝突する広告をただ縮小するのではなく
反対側に拡大することで「面積そのままにずらせる」場合はスコアが下がらないので
合計スコアの計算時に「ずらせる広告はずらした状態で計算する」ようにしました
これをint配列のリファクタリング前に実装したのですが、点数はそこまで変わりませんでした
おそらく試行回数が減って処理時間の短縮にはなってると思うのですが・・・
さて、ここから大きく分けて二択になりそうです
- しっかりローカルでテストケースを見て今の出力の不足部分を見極めて余った3秒をそこの改善処理に使う
- スコアが上がる遷移だけを許して1.7秒なので焼き鈍しに変えて4.5秒回す
いつもなら前者に走ってしまうところですが今回は苦手な焼き鈍しに挑戦してみましょう
まずは先ほども話に挙げたcolunさんの記事を読んでみます
(「はじめに」を読み始める)
あー、文脈がない問題が焼き鈍しに向いてるのか
じゃぁ「マラソン系といえば焼き鈍し!」っていう先の発言は撤回しないとですね
今回みたいな「文脈のない単純な問題は焼き鈍しが向いてそう」という発言に訂正します
(「焼きなまし法はベター山登りなのか?」を読み始める)
あ・・・思い出した
そうだ前回読んで理解したあの感覚が蘇ってきた
今は既に局所解に落ちてしまってるし
そもそも焼き鈍しに使える「良い性質」を持った「遷移」を
今はまだ定義できてない気がするな
とはいえ早合点な気がするのでもう少し読み進めてみる
(「探索空間は本当に高次元なのか?」を読み始める)
いや、そっか やっぱり早合点だったかも
今回の場合だと「1マス拡大」や「1マス縮小」で良さそうだな
貪欲でやる分には"拡大して衝突する広告は縮小して辻褄を合わせる"処理は
かなりよかったというかこれが得点上がる契機になったけど
焼き鈍しでやる場合はそういう複雑なことはしなくて良さそう
やーでもこれまた「俺が今までやってきたことって一体・・・?」になりそうだなぁ
今日は一旦、別ブランチ切って焼き鈍しでチャレンジしてみるけど
これで上手くいったら今までの実装ほとんど関係なくなるなぁ・・・
これ以上読み進める前に理解を深めるため、
試しに今の理解で実装してみようとしたけど
採択確率はいいとして遷移する方法を選ぶ確率はどうするんだろう
等確率でいいのかなぁ、ここも色々場合によって分けないといけないのかな
とりあえず等確率で書いてみるか・・・
いや、温度の扱いもよく分かってないや
先にもうちょっと読み進めよう
(「採択確率式の正当性」を読み始める)
(「メトロポリス・ヘイスティングス法がうまくいく条件」を読み始める)
あー、さっきの話出てきたな
採択確率で調整するから選択確率qは等確率でいいのか、なるほどねー
(「メトロポリス・ヘイスティングス法と温度」を読み始める)
そう、ここが一番大事なんだよなぁ
ここは前読んだときから変わってないというか
ここの概念はちゃんと覚えてた
「なぜ焼き鈍し法が強いのか」はここに集約されていると思っていて
ここは理解してたけどそれ以外のところをちゃんと理解してなかったんだよな
・・・あれ、温度管理の話出てこなかった・・・
まぁ十分高いところからゆっくり下げればいいんだろうけど
これはあれかな、問題によって"良い温度の下げ方"が違うからあえて書かなかったのかな
色々試しながらやってみるか・・・
(「おまけ1 … 遷移先候補をどう提案するか?」を読み始める)
お、さっきの疑問の話が出てきた
そうそう、ここは知りたい部分だったんですよね
勝手に「等確率でいいのかな」って結論づけちゃったけど
うーん、結論から言うと今回は「1マス拡大」「1マス縮小」を等確率で選択して良さそうだなぁ
(「おまけ2 … 温度管理について」を読み始める)
お、温度の話が出てきた! ありがたい!
おー・・・何もわからん・・・
この式をそのまま使ってもいいけど
ちゃんと理屈を理解した上で使いたい・・・
(「終わりに」を読み始める)
いやほんとこの記事は素晴らしい記事だと思います
読んだことない人にはぜひ読んでほしい
(「謝辞」を読み終わる)
うーん、とはいえ温度管理がやっぱ大事そうだなぁ
もうちょっとおまけ2の式について考察するか
・・・いやーわからん! 線形で温度下げちゃダメかな? ダメなんだろうなー
ダメなんだろうけどなんでpowやexp使った方がいいか全然想像がつかない
とりあえず適当に焼き鈍し書いてみた
ローカルで試したところ95点出ている
マジかー・・・貪欲でやってるのが97点だからほとんど差がないな
これ焼き鈍しのパラメータ調整がんばったら普通に超えそうだなぁ・・・
いやしかしこれ図を見ると差が歴然としてるな
焼き鈍しの方がやっぱ綺麗だわ
貪欲でやるとどうしても諦められてる真っ青な広告が結構あるけど
焼き鈍しだとだいぶ少ない、0ではないけど十分少ない
いやでもこれあれかな、焼き鈍してから貪欲で詰めると実はうまくいったりする・・・?
ダメだ、そういうものではないんだなぁ
焼き鈍しの後に貪欲しても温度を下げてるのと変わらないからあんまり意味がないな・・・
そういえばscoreの計算式についてちゃんと考察してなかったな
これ全広告で90%取るのと90%の広告で100%取って残りを捨てるの、どっちの方がスコアが高いんだろう
あれか、二乗されるから面積がrの90%の場合は99点になるのか なるほど
実は面積を100%にする必要性は全然ないんだな
1%以上の広告を捨てるぐらいなら全部の広告で面積を90%にした方がいいのか
これはちょっと直感と一致してなかった、意外だ
・・・あれ?
さっき「焼き鈍し」の方が真っ青な広告が少ない、って言ったけど
今もう一回試したら「貪欲」の方が真っ青な広告少ないかも・・・?
たまたま「焼き鈍し」が1回だけ上手くいったのかな
とりあえず今、焼き鈍しの試行回数が334万回で95点ってところだから
せめて1千万回まで試行回数増やせないか高速化はしてみるかー
それでどれくらい点数上がるか次第だなぁ
・・・いや、これ言い出したら怒られそうだけど
Javaで試行回数稼ごうと高速化頑張るのなんか不毛な感じしちゃうなぁ・・・
まだ考察が十分じゃない感じがするから焼き鈍し頑張るよりも
もっと方針とか処理方法とかでまだ稼げる得点がありそうな気がする
一旦、焼き鈍しはここまでにして元の方針に戻ろうかな
3秒あれば点数上げる方法がまだある気がする
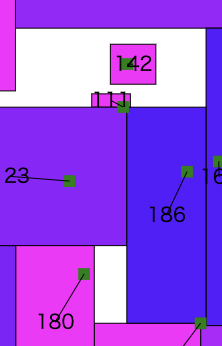
いやー、やっぱ縮小の仕方が大事だなぁ
前にあげたこの図は別にコーナーケースではなさそう
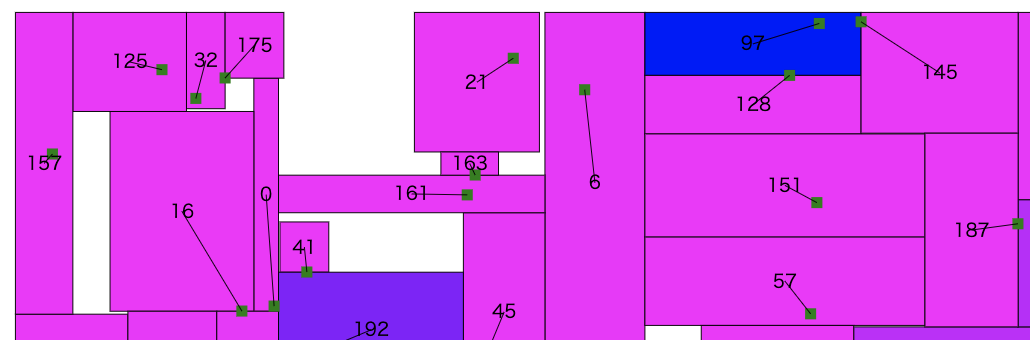
この図の97番の広告は一見、周りが綺麗に埋まっててどうしようもないように見える
というか今の自分の実装だと97番の広告を左に拡張しようとしたとき
6番の広告の右を1ピクセル縮小しようとするから縦幅がデカすぎてスコアが小さくなると判定されて不採用になって詰んでる
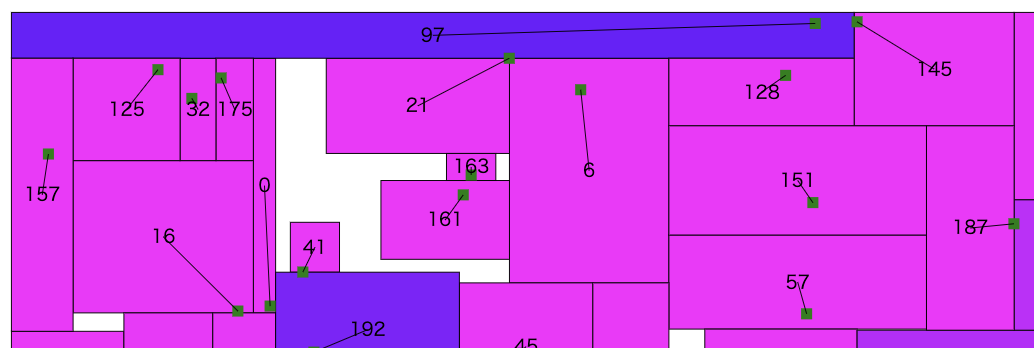
でも実はこんな風に横長にすればしっかり面積を稼げて
なおかつ周りの広告はちゃんと別のところで面積を稼げるので合計スコアは上がる(972488235->974101798)
つまり「左に拡張 → 周りの広告の右を縮小」っていう反対側かつ1ピクセルだけのパターンだけではなく
「左に拡張 → 周りの広告の上をごっそり縮小」みたいなパターンがないと
この状況は打破できない、ということかー・・・
いやでもこの状態からの遷移は無理があるな
結局それこそ焼き鈍しみたいにもうちょっと遷移に余裕がある段階で97番の広告に左へ伸びてもらわないと駄目だ
やっぱこれよりいい得点取るためには焼き鈍しかー 焼き鈍しだなぁ
まぁでもこれは遷移のさせ方を工夫しないと駄目だな
普通にやったら97番より左の広告が先に上を占めちゃうから
97番の広告が先に左に伸びるような遷移方法・・・
そんな恣意的な何かをルールというかコードで実装する方法があるのか・・・?
眠くなったのでお昼寝
そして思い浮かぶアイデア
スコアを意識しないのであれば広告はなんとなく10000x10000が最大サイズだと思っていたけど
他広告のx,yによる制約があって実はもっと最大サイズが小さくなってしまうんだということに今気付いた
これを各広告について「理論上最大面積」を先に求めておいて
その「理論上最大面積 / r」が低い順に広告を広げてあげれば
割と上手くいくのでは、というアイデア
理論上最大面積は厳密に求めようとすると大変だけれど
- できるだけ左に伸ばす
- できるだけ上に伸ばす、伸ばせなくなったら左を縮小する(左を縮小できなくなったら次のステップへ)
- できるだけ右に伸ばす、伸ばせなくなったら上を縮小する(上を縮小できなくなったら次のステップへ)
- できるだけ下に伸ばす、伸ばせなくなったら右を縮小する(右を縮小できなくなったら次のステップへ)
- できるだけ左に伸ばす、伸ばせなくなったら下を縮小する(下を縮小できなくなったら終了)
という実質4ステップでx,yから見た四象限それぞれの最大面積が求まる
のでその中で一番でかい象限の面積を「理論上最大面積」ということにすればなんとかなるのでは・・・?
とりあえず実装してみる、多分計算量は十分小さいはず・・・!
あー駄目だ・・・0023.txtの198個の広告があるパターンで15秒もかかる・・・
マジか・・・そんなに時間かかるか・・・
うーん手軽な高速化も思いつかない・・・
とりあえず19時になったのでAPEXのデイリーをこなす
デイリーをこなし終わったので戻ってきた
一旦、5秒制限を忘れて上記の理論上最大面積を使った実装を始めたけど
これ思ったより活かせないな・・・
まず四象限のどれかに偏るのでその最大面積の値をそのまま使うとかなり歪になってしまうし
では使わずに優先順位だけに使う、ってなると結局さっきの97番の広告が横に伸びない
うーん、「面積の広げやすさ」「自由度」みたいな観点はかなり大事な指標だと思ったんだけどなぁ
やはりscoreに直結しない要素を絡めようとすると得点に繋がらないなぁ
本当は10000x10000ピクセル全てについて
「どの広告に使われるべきか」みたいな指標を持つのがいいんだろうけど
単純に考えて計算量が大きすぎるんだよなぁ
あとそもそも広告はrより大きいことにメリットが一切ないから
(スコアは下がるし他の広告が使えるはずだった面積が減るので)
基本的に10000x10000が埋まることはほとんどなくて
99点(49.5億点)を取る分には全広告を90%の面積にするだけで達成できるから
なんだかんだ10%弱は空くと思うんだよなぁ
ちゃんと調べてみたら80%しか面積使ってなかった
まぁ80%でも96点(48億点)は取れるからなぁ・・・
なるほど・・・ここから今の空き地を半分埋めないと
99点(49.5億点)には辿り着けないのか・・・
うーん、そもそも状態を1個しか持たない今の解法でいいんだろうか
コピーが簡単にできる状態の持ち方を思いついていないので
今は状態を1個しか定義していないけれど
このままだと例えばビームサーチはもちろんできないし
多様性の確保が全然できないんではなかろうか
よくよく考えるとそこまで大変でもないのでは・・・?
1ずつの拡大/縮小であれば別広告との衝突判定が軽いことは分かっているので
状態、といっても純粋に「広告の数 * 上下左右」の0〜10000だけだな
高々800次元か 800次元のコピーならそんなに重くないよな・・・
明日は平日だから今日はあまり夜更かしできないけれど
平日にちょこちょこ状態を手軽に扱うリファクタリングはしてみてもいいかも
そしたら次の土日で何かしらいいアイデアを活かせたりするかも・・・?
1ピクセルずつの拡大/縮小じゃなくて
任意のサイズに変更、っていう遷移でもいい気がしてきた
衝突判定もそこまで重くないはず
いやでも意味あるのかなそれは・・・
局所解から抜け出すのには有効そうだけど
それはもっと早い段階で防ぐべきことな気もする・・・
そもそも衝突判定が必要なんだろうか
提出時には制約を満たしていないと0点になるから
各広告が正の共通面積を持たないように、衝突しないようにしないといけないけれど
例えば焼き鈍しは正の共通面積を持つことを許容しないと
遷移確率0の壁が歪に出現して上手く機能しないのでは?
もちろんスコアでデメリットは与えるべきだろうけどその値の調整も難しいな
できれば共通面積の広さに応じて負のスコアを与えたいけれど
これ計算コストがかかって試行回数に影響しそうだなぁ・・・
いや1個の広告のサイズを変えるだけなら共通面積の広さってそんなに求めるの難しくない・・・?
どうだろう・・・?
とりあえず各広告を1x1から始める必要はないなー、と思うなどした
一旦、sqrt(r)を1辺とする正方形で始めておいて
評価関数に任せて徐々に共通面積を減らしていってくれればそれでOKなのでは
実際に実装して試したいけれど、コードをもう書く元気がないので今日は終了
仮眠をとったらちょっと元気が出たので
- 開始時にsqrt(r)を一辺とする正方形で開始
- 共通面積の広さに応じて負のスコアを与える
- 1ピクセルの拡大/縮小で共通面積がどれくらい増減するかを返す関数を実装
で焼き鈍しを実装してみた
けど最初から正方形だと1ピクセルずらしても共通面積が変わらないので
全然うまくいかなかった
3日目(2021年3月8日)
平日は全然取り組む余裕がない
とうとう1位が49.5億点(99%)をとってしまった
これはつまり全ての広告の面積がrの90%を満たしているのと同じくらいのスコア
1位を狙うなら自分も残りの空き地を半分にしないといけないのか・・・シビアすぎる・・・
「面積100%にしなくていい、ってことは全部の広告を0%から始めて徐々に大きくしていけば上手くいくのでは?」
というアイデアが定時後にふと浮かんだ
が、実はこれは「score順でPriorityQueueに詰めて四辺を1ずつ大きくする」という形で既に実装済みだった
ただ「大きくできなくなった広告は諦めてQueueに入れない」という処理を入れていたので
青い広告もあれば100%を達成できている広告もあって・・・という感じになったわけで
この諦める処理を諦めなければ上手くいくかも?
あとこれは上のアイデアと上手く絡められていないけれど
邪魔な広告は1縮小とかではなく1x1まで縮めて拡大をやり直しにしたほうが
最終的に上手くいきそうだなー、とも思った
5秒の処理時間制限を無視して理論上最大面積を使っていろいろ実験したけど
あまり上手くいかなかった・・・
1x1に縮めてやり直す方は何回やり直しても同じ結果になりそうだから
どう実験すればいいかイメージがつかないんだよなぁ
4日目(2021年3月9日)
昨日は22時に布団に入って今朝6時前に目が覚めた
ほんとAHC001が始まってから布団に入る抵抗がなくなり
とても快眠できるようになった、実に幸せだ
結局、寝る前には何もアイデアを閃かなかったけれど
「全部の広告のrに対する面積比を少しずつ大きくしながら試行錯誤する」
っていうアイデアはやり方次第で上手くいきそうだなー、とは思った
例えば残り時間に比例して徐々に面積を広げることにして
ランダムに選んだ広告をランダムな縦横比で前述した面積比に変更する、
他の広告と正の共通面積が発生したら不採用、
みたいな遷移で乱択をするだけでも割と上手いことお互いがお互いを避けてくれるのでは? とか
これはこれで「正の共通面積が発生しているか」の判定をどう高速に行うか、
試しに実装してみてどれくらいの試行回数が稼げるかは実験してみてよさそう
あとは「どうすれば提案確率を均せるか」という課題かなぁ
ランダムに選んだ4辺を1ずつ拡大/縮小する方法はトータルで見ると
斜めへの提案確率が高くて一方向への提案確率が低いことにさっきまで気付いてなかった
これは焼き鈍しをする上でも良くない性質なので
トータルで見たときに提案確率が等しくなるような選び方をしないといけないなー、と思った広告
あともう一個勘違いしていたことがあって
そもそも広告はrより大きいことにメリットが一切ないから
(スコアは下がるし他の広告が使えるはずだった面積が減るので)
と思っていたけれど 99/100 < 100/101 なので
面積を100%ピッタリにできない場合は少し大きいほうがスコアが高くなることはあるんだなー、ということに気がついた
なので脳死で面積がrより大きくなることを禁止してはいけなくて
スコアが上がるならOK、みたいな少し緩い制約で縛らないといけないんだなー、と思った
private double score(int r, int area) {
return 1.0 * Math.min(r, area) / Math.max(r, area);
}
private void solve() {
int count = 0;
int total = 0;
Random rand = new Random();
for (; count < 10; total++) {
int r = rand.nextInt(2000000) + 1;
int x = rand.nextInt(Math.min(r, 10000));
float y = 1.0f * r / x;
int mid = Math.round(y);
if (score(r, x * (mid - 1)) > score(r, x * mid) || score(r, x * mid) < score(r, x * (mid + 1))) {
System.out.println(String.format("r=%d, x=%d -> %f %f %f", r, x, score(r, x * (mid - 1)), score(r, x * mid), score(r, x * (mid + 1))));
count++;
}
}
System.err.println(total);
}
---
r=19294, x=7819 -> 0.405256 0.810511 0.822526
r=11739, x=8162 -> 0.000000 0.695289 0.719125
r=434705, x=9152 -> 0.968454 0.989508 0.989549
r=8715, x=6037 -> 0.000000 0.692714 0.721799
r=26069, x=4754 -> 0.729449 0.911811 0.913932
r=8793, x=5902 -> 0.000000 0.671216 0.744917
r=1491745, x=8500 -> 0.991456 0.997154 0.997156
r=19782, x=7977 -> 0.403245 0.806491 0.826627
r=24895, x=7168 -> 0.575859 0.863788 0.868269
r=3616, x=2478 -> 0.000000 0.685288 0.729621
5398
「一辺をある値に固定した場合にもう一辺をroundで丸めた値にした場合、
スコアは最適か、それとも1ずらしたほうがスコアが上がるか」
をすごい雑だけど実験した
とりあえず500回に1回ぐらいはroundで丸めた値より1増やしたほうがスコアが上がることがあるみたい
逆に1減らしたほうがスコアが上がるパターンは100万回試してもなかった
(本当は数学的に証明できるのかもしれないけど全然式を思いつかなかった)
「正の共通面積が発生しているか」の判定を高速に行うのむずい・・・
1ピクセルだけ拡大、というか線分と矩形の判定は簡単だけど
矩形と矩形はきつい・・・全パターン網羅しようとするとどうしても処理が重くなりそう
・・・あれ? 全然そんなことなくない・・・?
ググって気付いたけどよくよく考えたら昔、散々ゲームで矩形と矩形の当たり判定実装したな
そっかー、各辺の位置関係が矛盾してないか見るだけか めちゃくちゃ軽いな
ランダムな縦横比で指定した面積にするコード、思ったよりめんどくさい
数値は0〜10000、矩形は(x,y)を必ず含まなければならない、っていう制約が
2回minやmaxを取る必要が出てきて乱数で出すべき値が計算しにくい
実装し終われば大したことないんだろうけど最初がめんどくさい・・・
後から使いやすいようにちゃんと関数化しとかないと後悔するなこれ
(↓これは読まなくていいです)
int mode = rand.nextInt(2);
if (mode == 0) {
int low_limit = 1 + space.r / 10000;
int x = low_limit + rand.nextInt(10001 - low_limit);
space.right = Math.max(space.x, x);
space.left = rand.nextInt(space.x);
space.right = space.x + 1 + rand.nextInt(Math.max(10000 - space.x, low_limit));
int y = Math.max(1, Math.round(space.r / (space.right - space.left)));
space.top = space.y - rand.nextInt(Math.min(space.y + 1, y));
space.bottom = space.top + y;
} else {
int low_limit = 1 + space.r / 10000;
space.top = rand.nextInt(space.y);
space.bottom = space.y + 1 + rand.nextInt(10000 - space.y);
int x = Math.max(1, Math.round(space.r / (space.bottom - space.top)));
space.left = space.x - rand.nextInt(Math.min(space.x + 1, x));
space.right = space.left + x;
}
元々こんな感じにゴリゴリ書いててバグらせたり確率が偏ったりしてたけど・・・
/**
* 区間[0,10000)から座標baseを含む長さlengthの区間をランダムで選出してその始点を返す
* @param length 長さ
* @param base 必ず含む座標
* @param random 乱数生成器
* @return 範囲の始点
*/
private int getRandomBegin(int length, int base, Random random) {
int lower_bound = Math.max(0, base - length);
int high_limit = Math.min(base + 1, 10001 - length);
return lower_bound + random.nextInt(high_limit - lower_bound);
}
こんな感じで関数化すれば・・・
/**
* ランダムなオフセットかつ与えられた面積の矩形に変更する
* @param area 面積
* @param random 乱数生成器
*/
public void changeRandomArea(int area, Random random) {
int width;
int height;
int lower_bound = (area + 9999) / 10000;
// 縦と横どちらを先に決めるかは1/2にする
if (random.nextInt(2) == 0) {
width = lower_bound + random.nextInt(10001 - lower_bound);
height = Math.max(1, Math.round(area / width));
} else {
height = lower_bound + random.nextInt(10001 - lower_bound);
width = Math.max(1, Math.round(area / height));
}
this.left = getRandomBegin(width, this.x, random);
this.right = this.left + width;
this.top = getRandomBegin(height, this.y, random);
this.bottom = this.top + height;
}
できた! めっちゃシンプルになった!
rectangle 17 does not contain point 17
あれー・・・座標含んでないって言われる・・・
どこがバグってるんだろう・・・
int lower_bound = Math.max(0, base - length);
あー、これ間違ってるな
base=10, length=10だったとして
0は[0,10)があり得るから10含んでないな
int lower_bound = Math.max(0, base + 1 - length);
こうかな・・・?

よし、大丈夫そう
スコアは全然出てないけど広告同士は被ってないし
制約もちゃんと満たしてるみたい
・・・いろいろ調整したけど細長いな・・・
一個細長い広告ができると後から追従する広告もぶつからないように伸びるから全部同じ方向に細長くなる・・・
width = lower_bound + random.nextInt(10001 - lower_bound);
あとこれもよくないな・・・希望面積100でも幅10000にしようとしたりしちゃうので
int range = Math.min(10001, lower_bound + area) - lower_bound;
width = lower_bound + random.nextInt(range);
せめてこうすべきか
・・・うーん、変わらんな・・・元からrが1万より大きいからかな・・・
あー、違うな・・・先に選んだ軸を一様分布な乱数で選んじゃうと
もう片方の軸はほぼ50%の確率で1になっちゃうのか そりゃ細長くなるわ
うーん、かといって縦横を一様分布な乱数でそれぞれ選んで
後から面積に合わせて縮小して・・・とかだと正方形の確率が高すぎる気がするんだよな
まぁ細長いよりマシかな・・・やってみるか
やー、それもめんどいな
面積16万で1,10000とか選ばれた時に縦横それぞれ4倍にすると
4,40000になってオーバーするからダメなんだよな
つじつま合わせがめんどい・・・えー、どう乱数発生させるのが一番いいかな・・・
縦と横の長さの差を決め打つのが楽な気がしてきた
int diff = random.nextInt(area * 2 - 1) - (area - 1);
int width = (int)Math.round((Math.sqrt(diff * diff + 4 * area) - diff) / 2);
int height = width + diff;
やー、でもこれもダメだ
大きい長さの差が選ばれることの方が多いから細長い確率が高い
あと幅や高さが平気で1万を超える
もう仕事開始の時間か・・・時間切れだなぁ
続きは定時後か明日の朝かなぁ
5日目(2021年3月10日)
昨日は仕事が終わったら疲れててそのまま爆睡してしまいました
そしてAPEXのイベントが始まってしまったので今日は昨日の分と今日の分をこなすので精一杯でした
6日目(2021年3月11日)
あの熱意はどこへ行ってしまったんだろう・・・
正直、今は仕事とAPEXで頭の中がいっぱいです
7日目(2021年3月12日)
せっかくの有給なのに仕事のことで頭がいっぱい
このままでは土日も取り組めないので
まずはAPEXで頭を空っぽにして考える余裕を作ろうと思う
例えどんな順位になっても「AHC001は本気で取り組みました!」
「平日は仕事のことで頭いっぱいだったから仕方ない」
「休日は全力で取り組んだ!」みたいな感じで言うつもりだったけど
正直、びっくりするぐらい冷めてしまった・・・
いや逆かなぁ、最初の土日の熱意が凄かった
別に今もいろいろ軽く方針考えたりはするんだけど
最初の土日に時間と熱意をかけすぎて
なんか平日を挟んだ今、もう一度同じ熱意まで持っていくのがしんどい
パッと試せるような内容は試しちゃったし
ここから先へ進むために必要な熱意の量が足りないんだよなぁ・・・
実行時間が1708msだった元の解法について詰めが甘かったのでちょっと変更してみた
元々は以下のようなアルゴリズムでやっていた
- 各広告を(x,y)に1x1で配置
- スコアが小さい順に四方へ1拡大する(できない場合はしない、面積がrより大きい時もしない)
- 拡大できるか否かは先述のlongによるbit配列でチェック、拡大時に拡大した辺をtrueで埋める
- スコアが小さい順に四方に拡大してみる、拡大して衝突する広告は縮小して辻褄を合わせる
- 合計スコアが下がるならば不採用、合計スコアが上がるならば採用
- 全広告について行ったらもう一度スコアが小さい順にソートして繰り返す
- 4.5秒経ったら繰り返さずに終了する
この「スコアが小さい順に四方へ1拡大する」は簡単な処理時間が短いアプローチとしてやっていたけれども
実行時間が余っているならそんな舐めプをする必要はない
というわけで以下のように変えてみた
- 各広告を(x,y)に1x1で配置
- 最もスコアが小さい広告を四方へ1px拡大してみる、拡大して衝突する広告は縮小して辻褄を合わせる
- 四方向のうち最も合計スコアが上がる方向だけ採用
- 衝突する広告がスライドできる場合はスライドしてスコアは下がらない扱いにする
- 四方向とも合計スコアが下がる場合は次にスコアが低い広告について同じ処理を繰り返す
- 4.5秒経ったら繰り返さずに終了する
焼き鈍しも何も関係ないけど、元のアルゴリズムより優秀なはず!
今の最高スコア更新できるのでは!? 提出!!
ダメでした、下がりました
処理時間が4651msになってます
なるほど、このアルゴリズムだと処理時間に余裕がないテストケースもあるんだな・・・
元々の方針の簡易的な拡大は舐めプではないことがわかった瞬間でした
というか一個でも変更があったら関係ないやつまで含めて最初からやり直すのは流石に無駄が多すぎるなぁ
でも直接触ってない広告の状況も変わってるからスコア順に確認した方がいいのは確かなんだよなぁ、うーん
8日目(2021年3月13日)
やー、でもスコアが小さい順に拡大して調整していくのが最善手な気がするんだよなぁ
そしてそれをするんだったら焼き鈍しとか別の手法で同じことをしようとするより
貪欲にルールベースで組み込む方が明らかに処理時間が減るような気がするんだよなぁ、うーん
今は上手く組めなくて処理時間が多くなっちゃってるけどもっと減らせそうな気がする
(3時間ほどの仮眠)
なぜ今まで気付かなかったんだろう
焼き鈍しで「提案確率を捻じ曲げず採択確率で調整する」ことが大事なのであれば
広告の座標を提案する確率も単に0〜10000から一様分布でランダムに選ぶだけで良かったのでは?
・・・ダメだ、ハズレが多すぎる
試行回数が全然足りなくなってしまう
あれ、タイムリープすればいいのでは?
元の貪欲の方のアルゴリズムの問題点は「どうしようもなく形を変えられずスコアを上げられない広告が発生すること」で
これは「前もってその広告は大きめに設定しておく」ことで他が頑張って別の場所を取ってくれることを確認済み(2日目の話)
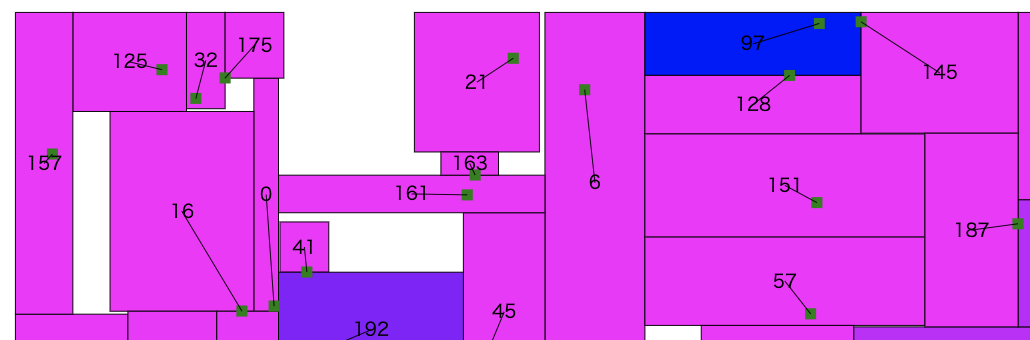
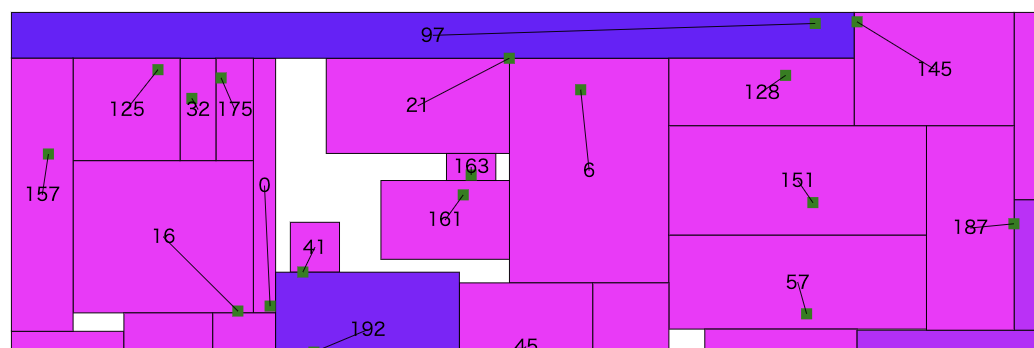
(再掲)
じゃぁ一度走り切ってしまって1.7秒で終わったところから記憶を残したまま最初からやり直して
「最終的にスコアが低かった順に面積を広げていく」という風にすればよりいいスコアが出せるのでは・・・?
そしてそれを繰り返せばどんどん良くなるはず
時間切れになったところでそれまでの一番良いスコアを提出、これか・・・!?
ただタイムリープするには入力値を退避しておくとかそれを復活するとかいろいろ準備が必要
まだ3時間しか仮眠取ってなくて頭が回らないのでタイムリープのためのコードを書く元気はまだない
どう書けばスマートか考えながらもう一回寝よう・・・
寝れなかったけど目を瞑って2時間くらい経った
落ち着いて考えれば全ての広告を1x1に戻すだけで初期状態に戻るので
そんなにタイムリープは難しくなかった
これまでのスコアの積をそのまま次回の評価関数にして繰り返してみる
あー・・・TLEした・・・
ちょっと時間管理が雑すぎた
全体を回すのは重いかな、と思って縮小は一切せず拡大部分だけタイムリープすることにして
その部分を4.5秒で切ったから、そのあとの処理が0.5秒以上かかってしまったっぽい
提出制限で30分暇だし次は全体を回してみるかー
全体を回した最終的なスコアを元に繰り返すようにしてみた
ローカルで回してる感じはかなり良さそう
30分待機、これは期待したい・・・!
173位→144位(48224254696->48435227971)
よしよし、自明な改良だった 伸びないはずはないと思ったけど伸びて本当に良かった
しかしもう100位以下に落ちてるのかぁ・・・
やっぱ別の方針でやらないと49億点台乗せるのは無理そうな気がするなぁ・・・
「理論上最大面積」、いろいろ問題があって諦めたけどもうちょっと詰めたら上手く扱えないかなぁ
いやでも仮に5秒以内に全広告について「理論上最大面積」がちゃんと求められたとしても
それをどうスコア最大化に結びつけるのかが難しいか
ややや、そうでもないかな・・・
理論上最大面積がrより小さい場合はその広告を最初から最大で配置して良い気がするんだよな
もちろん後からスコアが上がるような選択肢があれば縮小させるけど
まずはじめに先置きしておくのが大事な気がする
うーん、でも難しいよな 「理論上最大面積」
いや、一象限に限って言えば「ソートしてもう一方の軸の値が単調減少となる列」を抽出するだけか
O(NlogN) だな O(10000) よりはよっぽどいい
あとは各象限の単調減少列から上手いこと求めるアルゴリズムがないかなぁ
基本的には対角線となる象限2つから頂点を選んで
残りの象限2つの頂点に対して制約を満たすかチェックする、になるんだよな
O(N^3) だ・・・広告1個に対して O(N^3) だから全部やると O(N^4) か・・・
間に合わな・・・あれ、広告数が 200 でも 1.6 * 10^9 か 全然間に合う・・・? 定数倍次第・・・・?
ていうかあれか 200*200*200*200 にはならないな
仮に各象限に 50 ずつ分かれたとしたら 50*50*100*200 だから 5*10^7 だ 全然許容範囲では?
えー、組む・・・? やってみる・・・?
まだ土曜日だしいける・・・? 間に合うかな・・・?
本当に他の方針じゃなくてこれでいいんだろうか
とりあえずシャワー浴びてもう一回仮眠とってその間落ち着いて考え直すか・・・
仮眠するまでもなくシャワー浴びてる間にアルゴリズムは整理できた
どう使えるかまでは時間が足りなかったけど
とりあえず「5秒以内に全広告の理論上最大面積を求めることは可能か」ということの方が
今は関心が強いのでとりあえず仮眠を取る前に実装しちゃおうと思う
あっ・・・アルゴリズムは整理できてるけどそれをコードに落とすHP/MPが足りてない感じがする・・・
途中で挫折して仮眠しそう・・・いやでもこれ仮眠すると忘れそうだなぁ・・・でも文章にアウトプットするのもMPかかるし・・・
Arrays.sort(spaces, (s1, s2) -> {
if (s1.x == s2.x) {
return s1.y - s2.y;
}
return s1.x - s2.x;
});
for (int index = 0; index < n; index++) {
List<Point> rt = new ArrayList<>();
List<Point> rb = new ArrayList<>();
addAllTopBottom(rt, rb, spaces, index, +1);
List<Point> lt = new ArrayList<>();
List<Point> lb = new ArrayList<>();
addAllTopBottom(lt, lb, spaces, index, -1);
// TODO: rtとlbの任意の二点で作られる矩形に対してrbとltが含まれていないもののうち、もっとも面積が大きい値を調べる
// TODO: rbとltの任意の二点で作られる矩形に対してrbとltが含まれていないもののうち、もっとも面積が大きい値を調べる
}
private void addAllTopBottom(List<Point> topList, List<Point> bottomList, Space[] spaces, int index, int step) {
Space base = spaces[index];
int topY = 0;
if (index > 0 && spaces[index - 1].x == base.x) {
topY = spaces[index - 1].y + 1;
}
int bottomY = 9999;
if (index + 1 < spaces.length && spaces[index + 1].x == base.x) {
bottomY = spaces[index + 1].y - 1;
}
for (int i = index + step; 0 <= i && i < spaces.length; i += step) {
if (spaces[i].y <= base.y && topY < spaces[i].y + 1) {
topList.add(new Point(spaces[i].x - step, topY));
topY = spaces[i].y + 1;
}
if (spaces[i].y >= base.y && bottomY > spaces[i].y - 1) {
bottomList.add(new Point(spaces[i].x - step, bottomY));
bottomY = spaces[i].y - 1;
}
}
int limit = step > 0 ? 9999 : 0;
if (topY < base.y) {
topList.add(new Point(limit, topY));
}
if (bottomY > base.y) {
bottomList.add(new Point(limit, bottomY));
}
}
とりあえず各広告の四象限に存在する「四隅になり得る座標の列挙」までは書けた
やー、ここまで書いたならTODO部分も書き終わっちゃいたいな
あー・・・まずったな・・・これじゃダメだ
図を描かないと伝えるのが難しいけど図を描くのがめちゃくちゃめんどくさい
とりあえず頑張って言語化すると「矩形を成す座標集合と含まれていないことを確認する座標の集合はそもそも質が違う」、かな・・・?
矩形を成す座標集合は広告のx,yじゃないけど、含まれていないことを確認する座標の集合は広告のx,yその物だから・・・
あれ、じゃぁもうそのままx,y投げちゃえばいいか 計算量は増えるけどその方が楽だな
/**
* p1listとp2listから選択した任意の2点から成る矩形のうちspacesの座標を含まない最も面積が大きい矩形に対応するp1の点とp2の点を返す
* @param p1list 矩形の座標集合
* @param p2list 矩形の座標集合(p1とは対角線側の象限)
* @param spaces 矩形に含まれてはいけない座標の集合
* @param exceptId spacesの対象から除外するID
* @return [p1の点, p2の点]
*/
private Point[] calcMaxArea(List<Point> p1list, List<Point> p2list, Space[] spaces, int exceptId) {
int maxArea = 1;
Point[] maxPoints = new Point[2];
for (Point p1 : p1list) {
for (Point p2 : p2list) {
int left = Math.min(p1.x, p2.x);
int top = Math.min(p1.y, p2.y);
int right = Math.max(p1.x, p2.x) + 1;
int bottom = Math.max(p1.y, p2.y) + 1;
boolean ok = true;
for (Space space : spaces) {
if (space.id == exceptId) {
continue;
}
if (left <= space.x && space.x < right && top <= space.y && space.y < bottom) {
ok = false;
break;
}
}
int area = (right - left) * (bottom - top);
if (ok && maxArea < area) {
maxArea = area;
maxPoints[0] = p1;
maxPoints[1] = p2;
}
}
}
return maxPoints;
}
よし、だいぶシンプルな関数になった
簡単なケースで試してみて・・・
あれ・・・? なんか全然値が小さいぞ・・・?
ぎゃーダメだこれ!!!
そうか、最も面積が大きい矩形の座標がその象限にある座標のx,yと一致するとは限らないのか・・・!
実は別の象限の制約でその象限にはない座標のx,yが一番大きくなることがあるんだな、ぐぇーやられた
じゃぁそもそもこの方針がダメだな、ぐぬぬ・・・
えー、やっぱ「理論上最大面積」求めるのめっちゃむずいな・・・うーん・・・
仮眠をとろうと布団に入ったのですが、だいぶ混乱してそう
ちゃんと左上/右下の組と左下/右上の組で確認してるので網羅はちゃんとできてるはず
・・・ということでコードを見直してたら誤字ってどちらも左下/右上でやってました そりゃ網羅できないよ
もう一個、自身の座標を除外するために渡しているexceptIdが全然違う値を渡していたのでそれを修正
198個あるSeed23のテストケースで実行・・・!
おぉ、20msで計算できた! 全広告の理論上最大面積が超高速で求まった!
えっ、ここまで短くなるとは思ってなかった
これで安心して仮眠できるな
さてさてこの理論上最大面積、どう使おうかな
だいぶ無理やり感あるけどあれかなー
一回とりあえず回してみて「理論上最大面積に対してどれくらい面積が小さいか」の比を出して
それが著しく低い広告は最初から理論上最大面積にしておく、とかかなぁ
仮眠をとってAPEXのチャレンジをこなして晩ご飯も食べて
あとはもう寝るまで何も邪魔するものはない!
・・・と思ってたけどめちゃくちゃ眠い、全然頭が回らない
仮眠が足りてなかったか・・・
理論上最大面積の値にするのが正しいとは限らないのが微妙なんだよなぁ
せっかく20msで求められるようにしたけど正直使い道がないなぁ・・・
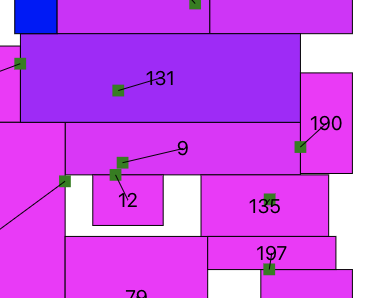
あー、また出てきたこういうやつー
結局、人間が見たら「こうすればいいのに」って分かる
自明な改善がまだ組み込みきれてないんだよなぁ
でもこれ連鎖してるから計算量簡単に爆発しそうだよなぁ
「131右に伸ばしたい→190を下にずらしたい→135を左にずらしたい」じゃなくて
「135をずらせるからとりあえずずらす→190をずらせるからとりあえずずらす→131が右に伸ばせた!」
の方がいいのかもしれないなぁ
とりあえずスコア変えずに余裕がある広告はひたすらいろいろ動かしてみる・・・?

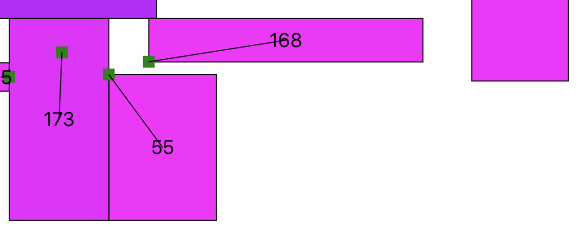
これもそうなんだよなぁ
物理演算ができたら一番良さそうなんだけどな
すべての広告をスライムみたいなやわらかい素材にして
(x,y)からrの圧力で押し出していくと勝手に最適な面積になりそう
最初は縦だったけど圧力に押し出されて横にグニャって伸びる瞬間があったりとか
そういう感覚がプログラムに落とせるとかなり良さそうなんだけど・・・
それこそ評価関数を上手く設計して焼きなますと上手くいくんだろうなぁ
普段からぐねぐね各広告が色んな形に変わっていて
徐々に評価が良い方へ良い方へ確率的に収束させる・・・
今回の問題はそれが一番良い気がする
9日目(2021年3月14日)
とうとう最終日
正直、今からスコアが上げるのは無理だと思っているけれど
コンテスト終わったら一切何もしなくなるだろうし
終わる前に焼き鈍し周りの練習をしようかなー、と思った
ダメだー、そもそも提案確率をどういじればいいかがわからんー・・・!
多分、温度とか関係なく「理論上最大面積より大きい」「他の広告と衝突している」「x,yを含まない」場合は
無条件で採択しなくて良いと思うんだけど、提案確率を一様にしたまま上記3条件で回すと全然採択されない・・・
なんかうまいこと提案確率をいじらないと試行回数が稼げない・・・
それとも逆に「上記3条件のいずれかを満たす場合に採択しない」っていうのがそもそも良くないのかなぁ うーん
こう数学的にうまいこと組み立てて
「x,yを含む理論上最大面積より小さい面積の座標候補から一様に選択する」
ことができるような提案確率を実装できるとだいぶ良さそうなんだけど・・・!
(時間切れ)
1000行弱におよぶ長文/駄文、ここまでお読みいただきありがとうございました。