0. はじめに
量子コンピュータ Advent Calendar 2021 2日目の記事になります。
(五月祭用に書いていて,中止に伴いお蔵入りしていた記事です)
この記事では 超伝導量子コンピュータ の物理について紹介します。
工学博覧会企画だったので,読者として特に以下を想定しています。
- 量子コンピュータ に興味がある高校生・大学1, 2年生
そのため数式による説明は抑えて,概念ベースの説明としています。
ただし発展的な読者のために,数式ベースの説明も補足しています。
補足部分は折り畳んでいるので,興味がある方は展開してください。
以下について知識があると,スムーズに読み進められると思います。
- 高校物理
- 原子物理(水素原子)
- 電磁気学(LC共振回路)
- 量子コンピュータ基礎
- 量子コンピュータとは
- 量子ビットとは
- (量子力学)
- (調和振動子)
ちなみに今回の題材である 超伝導量子ビット はこんな見た目です。
こうした超伝導量子ビットの基礎となる物理について解説します。

出典:Gambetta, Jay M., Jerry M. Chow, and Matthias Steffen. npj Quantum Information 3.1 (2017)
目次
1. 超伝導量子コンピュータ色々
現在,量子コンピュータ の実現に向け,様々な物理系がその候補として提案されています。以下に挙げているのはその代表例ですが,これらを含む様々な物理系を対象として,研究開発が世界中で進められています。
- 超伝導
- イオントラップ
- 中性原子
- 光
- 半導体量子ドット
この中でも特に 超伝導方式 は,米IT大手のIBMやGoogleを筆頭に開発が進んでいます。(最近は,米機械大手のHoneywellや米スタートアップのIonQを筆頭に,イオントラップ方式も勢いを増しているとも聞きます。)(と,2021年4月時点では書いていましたが,この半年でさらに中性原子や光も盛り上がりを見せているように感じます。)今回はこの 超伝導量子コンピュータ に焦点を当て,その基礎を紹介します。
ただ一口に「超伝導量子コンピュータ」と言っても,大きく分けて以下の3種類が存在します。
- 電荷型
- 磁束型
- 位相型
代表例を挙げると,IBMやGoogleが主に研究開発を進めているのは 電荷型 であり,「世界初の商用量子コンピュータ」を謳ったカナダのスタートアップD-Waveの量子アニーラで用いられているのは 磁束型 です。これらの中で今回は,電荷型の超伝導量子コンピュータを取り上げます。(以下で「超伝導量子コンピュータ」や「超伝導量子ビット」と言う際には,電荷型を指すものとします。)
ちなみに現在の超伝導量子コンピュータは,以下のような見た目をしています。非常に格好が良いですが,シャンデリア様の部分は希釈冷凍器と呼ばれる冷却装置であり,本体である量子ビットは最下部の先端に格納されています。この希釈冷凍器については,量子コンピュータの大規模化に向けて再設計も進められているようで,十年ほど後には全く異なる見た目をしているかもしれません。

Image: IBM
2. 目標とするは人工原子の実現
量子コンピュータにおいて最も重要な構成要素は,量子ビット です。量子ビットとは,以下にあげるような量子力学的な二状態系であり,量子計算ではこうした系を駆使することで計算を実行します。
- 偏光(縦波 / 横波)
- 電子スピン・核スピン(↑ / ↓)
- 電子準位(基底状態 / 励起状態)
この内,超伝導量子コンピュータで用いられている 超伝導量子ビット は,最後に挙げた 電子準位 の考え方をベースとしています。電子準位とは,原子やイオンにおける電子のエネルギー準位であり,その 基底状態 と 励起状態 をもって量子ビットとすることができます。ここでは高校物理でも登場する分かりやすい例として,水素原子のエネルギー準位 を取り上げます。
水素原子のエネルギー準位は,下右図のように飛び飛びの値を取るのでした。
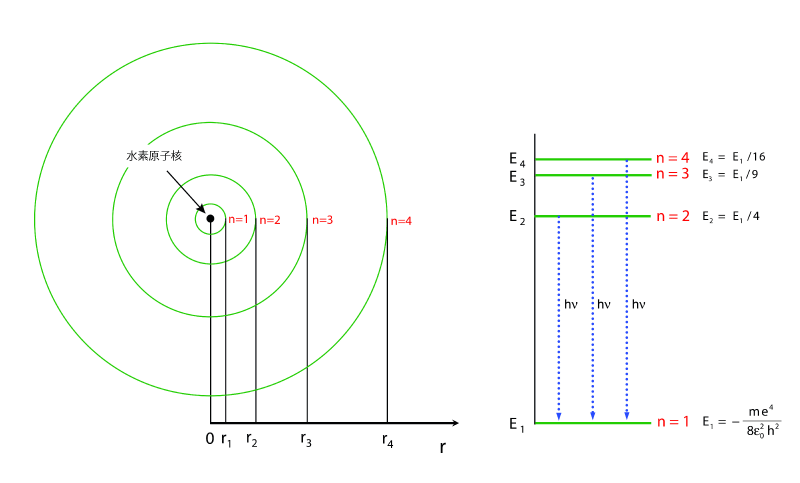
出典: [生命系のための理工学基礎「水素原子のエネルギー準位とリュードベリ定数を導出しよう」] (https://rikei-jouhou.com/rydberg-formula/)
図には $E_1$ から $E_4$ までのエネルギー準位が表されていますが,この中でも $E_1$ の基底状態 と $E_2$ の 第一励起状態 だけを他の状態から分離することができれば,それを 量子ビット として用いることができます。そして,この水素原子のエネルギー準位から $E_1$ の状態と $E_2$ の状態だけ取り出すことは比較的容易です。なぜならエネルギー準位が 非等間隔 となっているため,系にエネルギー $E_2 - E_1$ を与えると,基底状態が第一励起状態に励起される一方,他の励起が生じることは理想的には無いからです。
ただし,現実的にこうした原子そのものは扱いづらいため,こうした系をそのまま量子ビットとすることはありません。(イオントラップ方式では,同様の発想でイオンそのものを扱っていますが。)代わりに,このようなエネルギー準位をより扱いやすい形で人工的に再現することを考えます。超伝導量子コンピュータでは,電気回路 によって 人工原子 を作成し,その基底状態と第一励起状態を量子ビットとしています。
1.3 と 1.4 では,実際どのように電気回路で原子を再現しているのか見ていきます。その前に,人工原子として満たすべき要件を改めて確認しておきましょう。以上で簡単に見たように,実装すべき人工原子は次のような要件を満たしていると嬉しいのでした。
- 飛び飛び のエネルギー準位をもつ
- エネルギー準位が 非等間隔 である
この二点を念頭に,電気回路による人工原子作成の流れを追ってみましょう。
3. LC共振回路によるチャレンジ
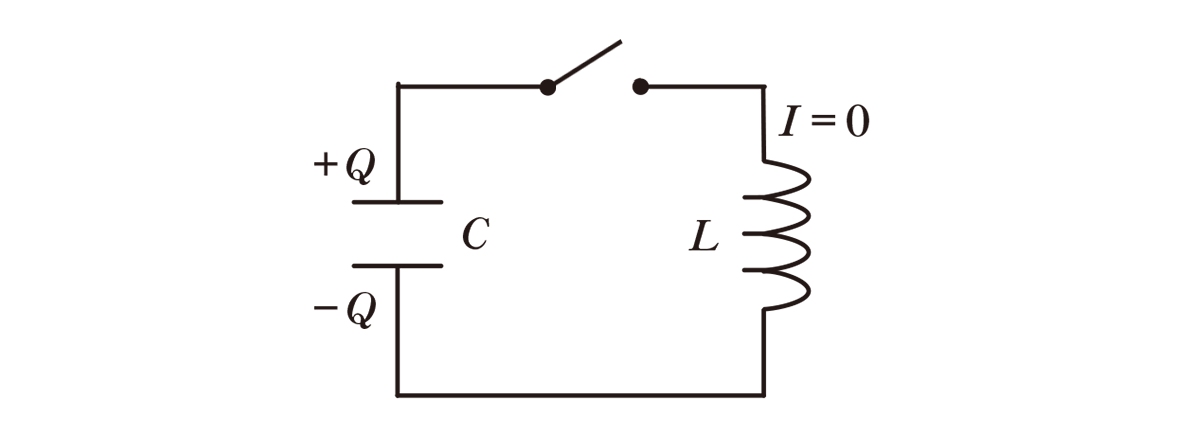
電気回路で原子の再現を目指すにあたって,ベースとなるのは高校物理でも学ばれる LC共振回路 です。LC共振回路とは,下図のように コイル と コンデンサ からなる電気回路のことでした。
LC共振回路はその名の通り 電気振動,つまり周期的な電流の変化を生じます。そして,この現象は以下のような対応関係において,力学における バネの単振動 と同一視することができるのでした。
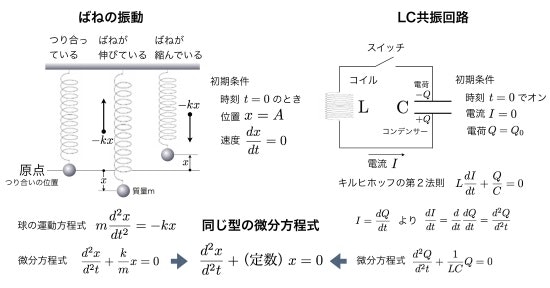
出典:空間情報クラブ「ラプラス変換|微分方程式やフーリエ変換との関係」
このようなモデルで表現できる現象を「調和振動」と呼び,モデルを「調和振動子」と呼びます。つまりバネによる単振動も,LC共振回路による電気振動も調和振動となっています。
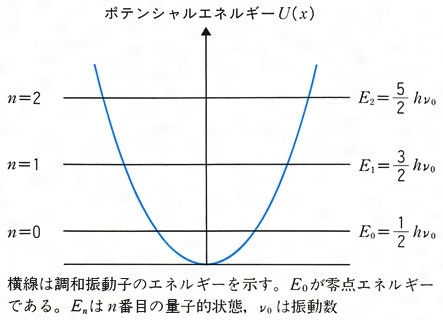
次に,LC共振回路を表現する調和振動子の 量子化 を考えます。ここでは量子化とは,LC共振回路を極低温に冷却して 超伝導状態 とする状況を想定してください。一般に調和振動子を量子力学的に取り扱うと,下図のようなエネルギー準位が現れるのでした。(ここだけ量子力学の知識を要してしまうので,未修の方は鵜呑みにしてください。)
出典:コトバンク 日本大百科全書(ニッポニカ)「零点エネルギー」
このようにして得られるエネルギー準位は,人工原子作成の二要件の内「飛び飛びのエネルギー準位をもつ」を満たしています。つまり,超伝導LC共振回路 によって飛び飛びのエネルギー準位を実現することが可能です。
では,もう一つの要件「エネルギー準位が非等間隔である」はどうでしょうか。上図からも見て取れるように,量子化した調和振動子のエネルギー準位は一般に 等間隔 となってしまいます。そのため,このままの超伝導LC共振回路では,人工原子や量子ビットとしては不十分です。
次の 1.4 では,この超伝導LC共振回路にさらなる工夫を加えることで,等間隔だったエネルギー準位を非等間隔とし,超伝導量子ビットが完成されるまでをご紹介します。
4. ジョセフソン接合により完成
では,超伝導LC共振回路 をどのように修正すれば,非等間隔 のエネルギー準位を実現することができるでしょうか。このことを考えるため,再び調和振動子 に立ち返ってみることにします。
「何をもって調和振動子と呼ぶか」という条件には同値なものがいくつか存在しますが,分かりやすいものの一つに ポテンシャル の形が挙げられます。ポテンシャルは,高校生の方には位置エネルギーと言った方が馴染み深いでしょうか。調和振動子では,ポテンシャルが変位の二乗に比例します。このようなポテンシャルを,調和ポテンシャル と呼びます。例えば,バネ定数 $k$ のバネによる単振動で位置エネルギーは,
U = \frac{1}{2}kx^2
であり,確かに調和ポテンシャルとなっています。またLC共振回路でも,磁束 $\Phi$ を座標とみなすことができて,電流 $I$ に対して $\Phi = LI$ が成り立つので,コイルに蓄えられるエネルギーは
U = \frac{1}{2}LI^2 = \frac{\Phi^2}{2L}
であり,同様に調和ポテンシャルとなっています。
以上の点に着目すると,調和ポテンシャルに修正を加えてあげれば,エネルギー準位を非等間隔にずらすことができるのではないか,と考えられます。そして,このような修正を実現することができるのが,小見出しの「ジョセフソン接合」です。ここではジョセフソン接合について簡単に紹介した上で,それがどのように 超伝導量子ビット に寄与しているか見てみます。
ジョセフソン接合とは,二つの 超伝導体 の間に薄い 絶縁体 を接合して,二つの超伝導体を弱く結合させた構造のことです。このような構造では,超伝導状態における電子対(クーパー対)が トンネル効果 で絶縁体を通過し,その結果 ジョセフソン電流 と呼ばれる電流が流れます。このジョセフソン電流 $I$ は,臨界電流 $I_c$ および 二つの超伝導体間の位相差 $\phi$ に対して,以下のように表されます(ここでは「超伝導体間の位相差」が分からなくても問題ありません。LC共振回路の例における,磁束 $\Phi$ に対応する量として捉えておいてください。);
I = I_c \sin(\phi)
このジョセフソン接合によって,LC共振回路のコイルを置き換えることを考えます。コイルに蓄えられるエネルギーは電流の二乗に比例していましたが,同様にジョセフソン接合に蓄えられるエネルギーも電流の二乗に比例するため,以下のようになります;
U \propto I^2 = ( I_c \sin(\phi) )^2 \propto 1 - \cos(2\phi)
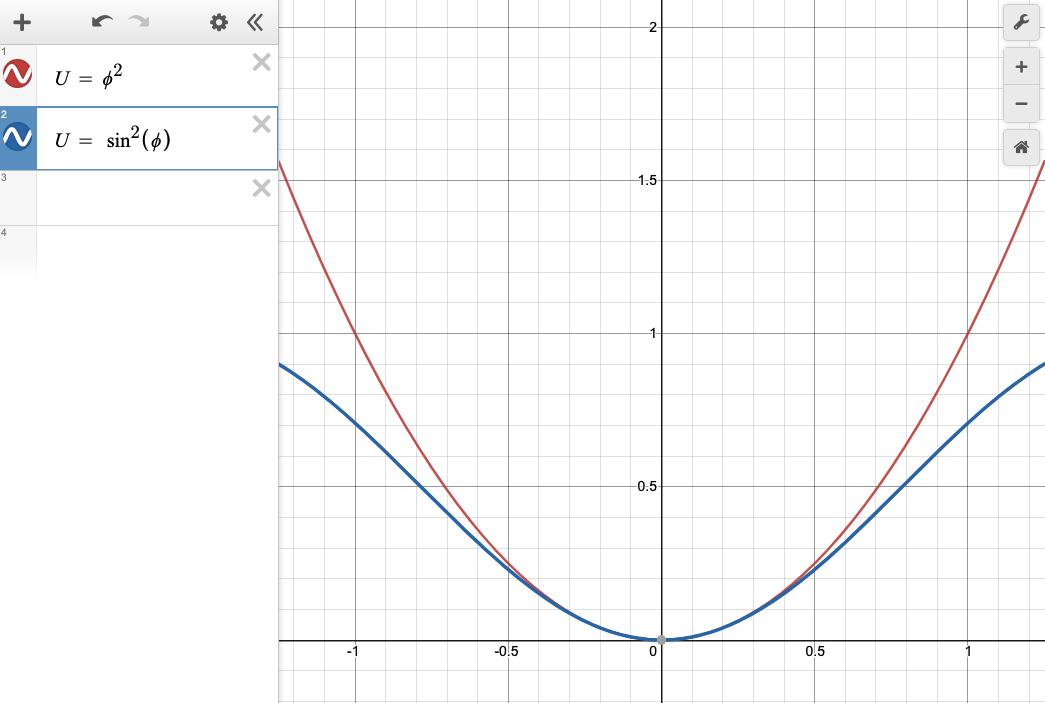
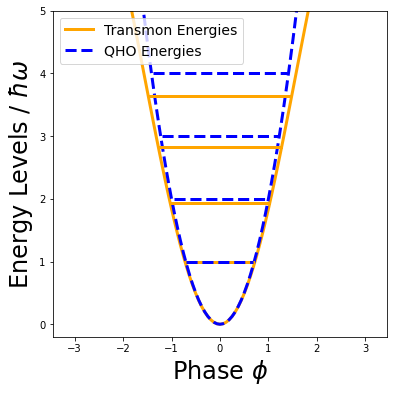
LC共振回路においてコイルをジョセフソン接合で置き換えた結果,上記のような形のポテンシャルが得られました。このポテンシャルを調和ポテンシャルと比較してみましょう。下図は,それぞれ単純化した調和ポテンシャル $U = \phi^2$ と ジョセフソン接合によるポテンシャル$U = \sin^2(\phi)$ を並べたグラフです。
ジョセフソン接合によるポテンシャルは,平衡点(ポテンシャルの底)付近で調和ポテンシャルと一致しており,平衡点から離れるほど乖離するものとなっています。このように,LC共振回路においてコイルをジョセフソン接合で置き換えた結果,調和ポテンシャルの形に修正を加えることができました。**このポテンシャルのもとで量子化を行うと,どのようなエネルギー準位が現れるでしょうか。**以下が,ジョセフソン接合のポテンシャル(橙曲線)と得られるエネルギー準位(橙横線)および調和ポテンシャル(青曲線)とそのエネルギー準位(青横線)の模式図です。
出典:Qiskit Textbook "Introduction to Transmon Physics"
こうして得られたエネルギー準位は調和振動子のものとは異なり,非等間隔 になっています。つまり,目指していた人工原子の二要件「飛び飛びのエネルギー準位をもつ」「エネルギー準位が非等間隔である」を達成することができています。
したがって,基底状態と第一励起状態だけを分離することが可能となり,これを量子ビットの基本形とすることができます。このような回路構成を基礎として,超伝導量子ビットの開発は今でも進められています。
5. 補足:数式ベースでの再説明
発展的な読者に向けた数式ベースの説明
「3. LC共振回路によるチャレンジ」再考
まずは LC共振回路 について考察します。以下のように設定します。
- $\Phi$:コイルを貫く磁束
- $V$:電圧
- $I$:電流
- $Q$:電荷
- $L$:自己インダクタンス
- $C$:静電容量
最初に磁束 $\Phi$ を 一般化座標 として,ハミルトニアン を求めましょう。
コンデンサのエネルギーは,ファラデーの電磁誘導の法則を用いて
K = \frac{1}{2}CV^2 = \frac{1}{2}C\dot{\Phi}^2
となります。またコイルのエネルギーは,$\Phi=LI$ の関係を用いて
U = \frac{1}{2}LI^2 = \frac{1}{2L}\Phi^2
となります。これらから,ラグランジアン は
\mathcal{L} = K - U = \frac{1}{2}C\dot{\Phi}^2 - \frac{1}{2L}\Phi^2
と求められます。これより,一般化運動量 は
\frac{\partial \mathcal{L}}{\partial \dot{\Phi}} = C \dot{\Phi} = CV = Q
と電荷に一致します。よって ハミルトニアン は,ルジャンドル変換 により
\mathcal{H} = Q \dot{\Phi} - \mathcal{L} = \frac{1}{2C}Q^2 + \frac{1}{2L}\Phi^2
と求められます。このような系は,共鳴周波数
\omega_c = \frac{1}{\sqrt{LC}}
で振動するような 調和振動子 となっています。
次に量子力学的な取り扱いに移行します。正準変数 ($\Phi$, $Q$) それぞれを
[\Phi, Q] = i \hbar
なる交換関係を満たす演算子で置き換える,正準量子化 を適用します。
また,$\hbar, C, \omega_c$によって正準変数を無次元化するために
\begin{align}
\Phi_0 &= \sqrt{\frac{\hbar}{2C \omega_c}} \\
Q_0 &= \sqrt{\frac{\hbar C \omega_c}{2}}
\end{align}
なる量を定義します。生成消滅演算子 $a^\dagger, a $をそれぞれ
\begin{align}
a^\dagger &= \frac{1}{2} \left( \frac{\Phi}{\Phi_0} + i \frac{Q}{Q_0} \right) \\
a &= \frac{1}{2} \left( \frac{\Phi}{\Phi_0} - i \frac{Q}{Q_0} \right)
\end{align}
とすれば, $[a, a^\dagger] = 1$ が成立し,ハミルトニアン は
\mathcal{H} = \hbar \omega_c \left( a^\dagger a + \frac{1}{2} \right)
と対角化することができます。ここで $a^\dagger a$ は個数演算子となります。
したがって エネルギー固有値 は,$n$ を自然数として
E_n = \hbar \omega_c \left( n + \frac{1}{2} \right)
と表せて,確かに 等間隔のエネルギー準位 となることが分かります。
「4. ジョセフソン接合により完成」再考
次に上記の議論で,コイルを ジョセフソン接合 により置き換えます。
まず,以下のように設定します。
- クーパー対の個数:$n = \frac{Q}{2e}$
- 磁束量子:$\Phi_0 = \frac{h}{2e}$
- ジョセフソン接合における二つの超伝導体の位相差:$\phi = 2\pi \frac{\Phi}{\Phi_0}$
- ジョセフソン接合の臨界電流:$I_c$
- ジョセフソンエネルギー:$E_J = \frac{I_c \Phi_0}{2 \pi}$
- ジョセフソン接合の静電容量:$C_J$
- 総静電容量:$C_\Sigma = C + C_J$
- クーロンエネルギー:$E_C = \frac{e^2}{2C_\Sigma}$
ジョセフソン接合においては,以下の電流-電圧特性が成り立ちます;
I = I_{c} \sin \phi \\
V=\frac{\hbar}{2 e} \frac{d \phi}{d t}
これよりLC共振回路のハミルトニアンは以下のように修正されます;
\mathcal{H} = 4 E_{C} n^{2}-E_{J} \cos (\phi)
第二項で表されるポテンシャルは,以下のように級数展開できます;
E_{J} \cos (\phi)=\frac{1}{2} E_{J} \phi^{2}-\frac{1}{24} E_{J} \phi^{4}+\mathcal{O}\left(\phi^{6}\right)
2乗の項は調和ポテンシャルであり,これだけでは先程と変わりません。
したがって,ここでは4乗の項まで考慮して,第二量子化を適用します。
先程と同様に $\phi, n$ に対し生成消滅演算子 $c^\dagger, c$ を次のように定義します;
\begin{array}{c}
q_{0}=\left(\frac{E_{\mathrm{J}}}{32 E_{\mathrm{C}}}\right)^{1 / 4}, \quad \phi_{0}=\left(\frac{2 E_{\mathrm{C}}}{E_{\mathrm{J}}}\right)^{1 / 4} \\
\hat{c}=\frac{1}{2}\left(\frac{\hat{\phi}}{\phi_{0}}+\mathrm{i} \frac{\hat{q}}{q_{0}}\right), \quad \hat{c}^{\dagger}=\frac{1}{2}\left(\frac{\hat{\phi}}{\phi_{0}}-\mathrm{i} \frac{\hat{q}}{q_{0}}\right)
\end{array}
このもとで,調和ポテンシャルの部分は先程と同様の結果になります;
\hbar \omega_0 = \sqrt{8 E_C E_J} \\
\mathcal{H}_0 = \hbar \omega_{0}\left(\hat{c}^{\dagger} \hat{c}+\frac{1}{2}\right)
また,4次の項は
\begin{equation}
\begin{split}
-\frac{1}{24} E_J \hat{\phi}^{4}&=-\frac{1}{12} E_C\left(\hat{c}+\hat{c}^{\dagger}\right)^{4}\\
&\approx -\frac{1}{12} E_C\left(3+6 \hat{c}^{\dagger} \hat{c} + 6(\hat{c}^{\dagger} \hat{c})^2 \right)\\
&= const. - \frac{E_C}{2} \hat{c}^{\dagger} \hat{c} - \frac{E_C}{2} \left(\hat{c}^{\dagger} \hat{c}\right)^2
\end{split}
\end{equation}
と近似できます。このもとで固有状態と固有エネルギーは
\begin{aligned}
\mathcal{H}|n\rangle &=E_{n}|n\rangle \\
E_{n} &=\left(h \omega-\frac{E_{C}}{2}\right) n-\frac{E_{C}}{2} n^{2}
\end{aligned}
となります。このときエネルギー間隔は
E_{n+1}-E_{n}=\left(h \omega-\frac{E_{C}}{2}\right)-\frac{E_{C}}{2}(2 n+1)
となっていて,確かに非等間隔なエネルギー準位が実現できています。
6. まとめ
本記事では,超伝導量子ビットの基本構造がどのような物理に基づいているかについてご紹介してきました。超伝導量子ビットを作成するための目標は「離散的」かつ「非等間隔」なエネルギー準位です。まず離散的なエネルギー準位を回路で実現するため,下左図のように超伝導LC回路を考えました。ただそのままでは等間隔となってしまうため,下右図のようにコイルに代わってジョセフソン接合(右下回路図中の橙部)を用いることで,非等間隔を実現しました。最新の超伝導量子ビットは様々な工夫が加えられ,より複雑な構造となっていますが,そうした基礎にはこのような考え方があります。
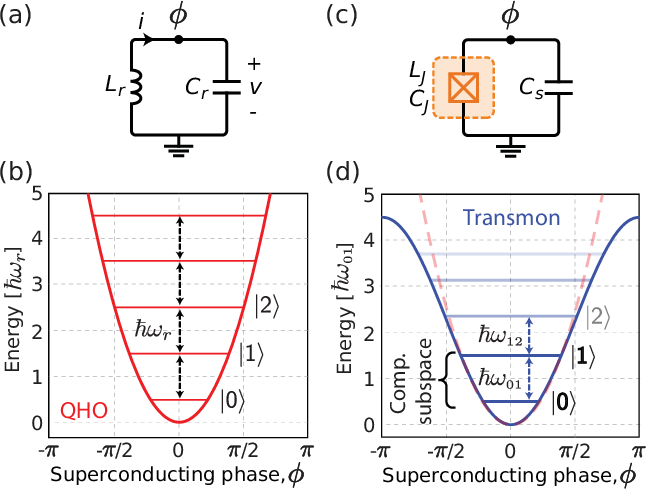
出典:Krantz, Philip, et al. Applied Physics Reviews 6.2 (2019)
7. 参考文献
- Girvin, Steven M. "Superconducting qubits and circuits: Artificial atoms coupled to microwave photons." Lectures delivered at Ecole d’Eté Les Houches (2011). (超伝導量子ビットに関する講義録で,入門には非常におすすめです)
- 向井寛人, 朝永顕成, & 蔡兆申. (2018). 超伝導量子コンピュータの基礎と最先端. 低温工学, 53(5), 278-286. (有り難い日本語解説です)
- Krantz, Philip, et al. "A quantum engineer's guide to superconducting qubits." Applied Physics Reviews 6.2 (2019): 021318. (工学的な視点に基づく解説が非常に参考になります)