【時系列】時系列データ予測　予測手法マップ #Python3

1.本記事作成の背景

業務都合により、生産量予測や売上予測を担当しており、”時系列”と名のつく専門書を読んでいるが、予測技術を俯瞰的に整理した資料がなかったため、自分なりに整理をしてみた。

2.技術マップ（モデルマップ）

2-1. マップ総論

整理するにあたり、予測の難易度を設定するにあたり
・定常・非定常
・線形・非線形
の２つの軸があるため、それぞれに対して適用に適している技術をまとめた。
なお、難易度は以下のように高くなっている。
・定常　＜　非定常
・線形　＜　非線形

上記を踏まえ、表の形でまとめた。

定常性/線形性	線形	非線形
定常	-自己回帰（AR,ARMA, ARIMA, SARIMA,ARCH,GARCH,ECM、構造VAR、ベイジアンVAR） -指数平滑化(一次指数、Holt-Winters) -状態空間（カルマンフィルタ） -深層学習(RNN,LSTM,GRU,Transformer) -ベイジアン動的線形 -Bass	-カオス解析（ロジスティック写像など） -状態空間 -深層学習 -確率的ボラティリティ
非定常	-自己回帰（ARIMA,SARIMA） -状態空間（拡張カルマンフィルタ、非ガウス型フィルタ、粒子フィルタ） -ベイジアン動的線形 -マルコフ・スイッチング	-カオス解析（ロジスティック写像など） -状態空間（拡張カルマンフィルタ、非ガウス型フィルタ、粒子フィルタ） -マルコフ・スイッチング

2-2. モデル別概要

2-2-1. 総論

技術マップに示したモデルの概要を以降に示す。

モデルを実際に遊びながら学べるように、ソースコードも以下に記載していく。

module.py

# 共通ライブラリをインストール
# 数値計算ライブラリ
import numpy as np 
import pandas as pd

# グラフ化
import matplotlib.pyplot as plt
import seaborn as sns

# 設定
import warnings
warnings.filterwarnings("ignore")

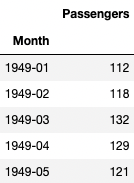
データのインポートは以下のとおり。

import.py

# Import data
INPUT_FILENAME = "AirportPassengers.csv"
df_pass=pd.read_csv(INPUT_FILENAME, sep=";",  index_col=0)

df_pass.head(5)

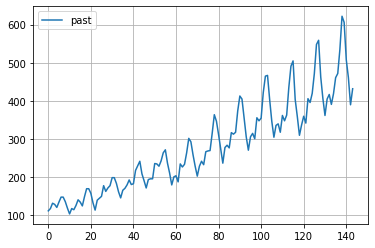
インプットデータの可視化は以下のとおり。

visualization.py

# DataFrameからArrayへ変換
array_pass = df_pass.values

# インプットデータを可視化
plt.figure()
plt.plot(array_pass,label="past")
plt.grid()
plt.legend()
plt.show()

2-2-2. 自己回帰モデル

英語名：ARモデル (Autoregressive model)

解析したいデータ系列があるとき、そのデータ系列の過去のデータに回帰させて未来の値を算出するモデル

ar.py

import statsmodels.api as sm

# ARモデル(p=5)
ORDER_P = 5
model = sm.tsa.ARMA(array_pass , order=(ORDER_P , 0))
result = model.fit(trend='c' , method='mle')
print(result.summary())

pred = result.predict(start=145,end=150)
print("prediction size =",pred.shape)
print("prediction values =",pred)

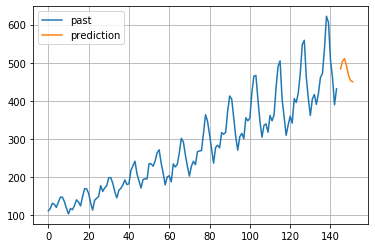
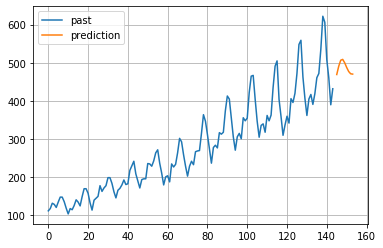
# 予測データも可視化
plt.figure()
plt.plot(list(range(0,144)), array_pass, label="past")
plt.plot(list(range(145,152)), pred, label="prediction") #予測値リストのサイズに合うようにrangeの区間を設定。
plt.grid()

plt.legend()
plt.show()

2-2-3. 移動平均モデル

英語名:MAモデル (Moving Average model)

解析したいデータ系列があるとき、ある時点tのデータと前後の項（例：MA(3)だったら、yt-1, yt, yt+1の３項）で平均をとり、変動要素を取り除くモデル。

moving_average.py

import statsmodels.api as sm

# MAモデル(q=1)
ORDER_Q = 1
model = sm.tsa.ARMA(array_pass , order=(0 , ORDER_Q))
result = model.fit(trend='c' , method='mle')
print(result.summary())

pred = result.predict(start=145,end=152)
print("prediction size =",pred.shape)
print("prediction values =",pred)

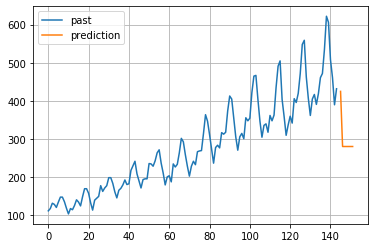
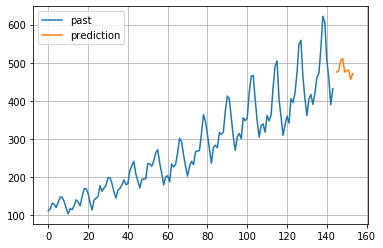
# 予測データも可視化
plt.figure()
plt.plot(list(range(0,144)), array_pass, label="past")
plt.plot(list(range(145,152)), pred, label="prediction") #予測値リストのサイズに合うようにrangeの区間を設定。
plt.grid()
plt.legend()
plt.show()

2-2-4. 自己回帰移動平均モデル

英語名： ARMAモデル (Autoregressive Moving Average model)

ARモデルとMAモデルの性質を含んだモデル。ARモデルに、白色雑音の現在と過去の値の線形和で表すモデル。
定常過程に対応可能。

arma.py

import statsmodels.api as sm

# ARMAモデル(p=5, q=3)
ORDER_P = 5
ORDER_Q = 3
model = sm.tsa.ARMA(array_pass , order=(ORDER_P , ORDER_Q))
result = model.fit(trend='c' , method='mle')
print(result.summary())

pred = result.predict(start=145,end=150)
print("prediction size =",pred.shape)
print("prediction values =",pred)

2-2-5.自己回帰和分移動平均モデル

英語名：ARIMAモデル (Autoregressive Integrated Moving model)

n階和分過程(=定常性のあるn回差分過程)をARMAモデルに導入したモデル。
和分過程で差分をとることで、定常性のあるデータ系列をもとにARMAモデルを使えるため、予測性が高い。
非定常過程も対応可能。

arima.py

from statsmodels.tsa.arima_model import ARIMA

# ARIMAモデル(p=5,d=1, q=3)
ORDER_P = 5
ORDER_D = 1
ORDER_Q = 3
model = ARIMA(array_pass , order=(ORDER_P , ORDER_D, ORDER_Q))
result = model.fit(trend='c' , method='mle')
print(result.summary())

pred = result.predict(start=145,end=152)
print("prediction size =",pred.shape)
print("prediction values =",pred)

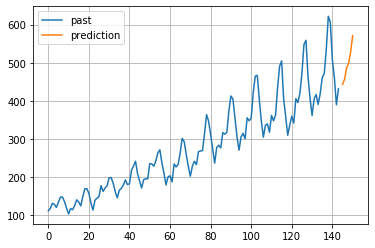
# 予測データも可視化
plt.figure()
plt.plot(list(range(0,144)), array_pass, label="past")
plt.plot(list(range(145,154)), pred, label="prediction") #予測値リストのサイズに合うようにrangeの区間を設定。
plt.grid()
plt.legend()
plt.show()

参考URL
1.日科技研
2.AVILEN "ARIMAモデル（自己回帰和分移動平均モデル）について分かりやすく解説！"
3.Logic of Blue "ARIMAモデルによる株価の予測"

2-2-6. 季節性自己回帰和分移動平均モデル

英語名：SARIMAモデル (Seasonal Autoregressive Integrated Moving model)

階差を取ることで季節性を除去する操作をARIMAモデルに適用。
具体的には、元データにARIMAを適用するだけではなく、周期性の方にもARIMAを適用したモデル。

sarima.py

import statsmodels.api as sm

ORDER_P = 5
ORDER_D = 1
ORDER_Q = 3

model = sm.tsa.statespace.SARIMAX(array_pass,order=(ORDER_P,ORDER_D,ORDER_Q),seasonal_order=(0,0,1,12),trend='c',enforce_invertibility=False)
result = model.fit(trend='c' )
print(results.summary())

pred = result.predict(start=145,end=150)
print("prediction size =",pred.shape)
print("prediction values =",pred)

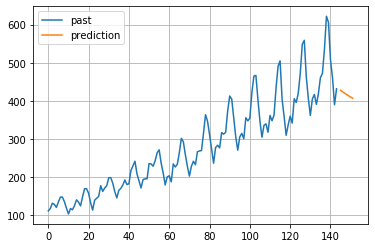
# 予測データも可視化
plt.figure()
plt.plot(list(range(0,144)), array_pass, label="past")
plt.plot(list(range(145,151)), pred, label="prediction") #予測値リストのサイズに合うようにrangeの区間を設定。
plt.grid()
plt.legend()
plt.show()

参考URL
1.AVLEN "定常時系列の解析に使われるARMAモデル・SARIMAモデルとは？"
2.未来を予測するビッグデータの解析手法と「SARIMAモデル」
3.Logic of Blue "Pythonによる時系列分析の基礎"

2-2-7.ベクトル自己回帰モデル

英語名：VARモデル (Vector Autoregressive model)

ARモデルを連立させて、多変量的に予測するモデル。
解析対象のデータ系列をベクトル形式で表現するため、このような名前がついた。
ARモデルは、自身のデータのラグのみを取るが、VARモデルは、自身以外のデータ系列のラグも含んで推定。
定常過程に対応可能。

var.py

from statsmodels.tsa.api import VAR

array_tmp = 2* array_pass#多変量用のダミーデータを作成。
print(array_pass.shape)
data = np.concatenate([array_pass,array_tmp],1)
print(data.shape)

model = VAR(data)
result = model.fit(trend='c' )

pred = result.forecast(data[-5:], 7)
print("prediction size =",pred.shape)
print("prediction values =",pred)
print("pred",pred[:7,0])

# 予測データも可視化
plt.figure()
plt.plot(list(range(0,144)), array_pass, label="past")
plt.plot(list(range(145,152)), pred[:7,0], label="prediction") #予測値リストのサイズに合うようにrangeの区間を設定。
plt.grid()
plt.legend()
plt.show()

1.Logic of Blue "VARモデル"
2.AVILEN "時系列データを解析するための様々なモデル"

2-2-8. 構造ベクトル自己回帰モデル

英語名：構造VARモデル (Structural Vector Autoregressive model)

通常のVARモデルでは、変数間の相関性はわかるが、要因（例：金融政策、天気）別の寄与度はわからない。
構造VARモデルは、ある評価したい時点のデータ（同時点）の係数行列を算出することで、寄与度も定量化する。

参考URL
1.金融政策と波及経路と政策手段、"第７章構造VARによる金融政策効果の計測"
2.西洋、"構造VARモデルによる日本経済の資本蓄積，所得分配，負債の動態分析"

2-2-9. ベイジアン・ベクトル自己回帰

英語名：BVARモデル (Bayesian Vector Autoregressive model)

VARモデルの係数を一つの値に決めるのではなく、平均と分散を持つと過程し、平均値を0もしくは1と置いてから分散を算出する手法。

参考URL
1.森川、泰"非定常時系列データとVARモデルによる金融政策の有
効性の分析"
2."保険，銀行と経済成長の相互作用に
関する研究"
3.川崎能典 "Bayesian Vector AutoRegression その手法の整理と予測能力の検証"

2-2-10. Bassモデル

英語名： Bass Model, Bass Diffusion Model, Bass product diffusion model
あるサービスや製品がどのように市場に普及するかをモデル化。特に、車やスマホなど繰り返し購入が発生しない商品の普及度合いを推定できるモデル。
最終的な累積購入者数mと、サービスインから時点tまでの累積購入者Y(t)と定義し、
他人に関係なく購入する新規購入者と、購入者から影響を受けて購入する新規購入者に分け定式化。

基本的なモデルを以下に示す。[1]
購入率をまずは定義する。

購入率を定義後、購入率の値を決める。
決め方の基本式を以下に示す。

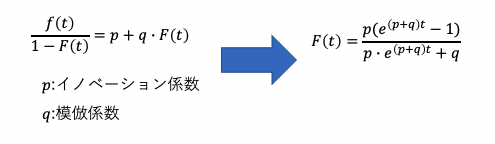
上記の式をpythonに落とし込むと以下のようになる。
（AirPassengerの値を使わないので注意。）

arima.py

from scipy.optimize import leastsq
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import numpy as np
#time intervals
t= np.linspace(1.0, 10.0, num=10)
# sales vector
sales=np.array([840,1470,2110,4000, 7590, 10950, 10530, 9470, 7790, 5890])
# cumulatice sales
c_sales=np.cumsum(sales)
# initial variables(M, P & Q)
vars = [60630, 0.03,0.38]

# residual (error) function
def residual(vars, t, sales):
    M = vars[0]
    P = vars[1]
    Q = vars[2]
    Bass = M * (((P+Q)**2/P)*np.exp(-(P+Q)*t))/(1+(Q/P)*np.exp(-(P+Q)*t))**2 
    return (Bass - (sales))

# non linear least square fitting
varfinal,success = leastsq(residual, vars, args=(t, sales))

# estimated coefficients
m = varfinal[0]
p = varfinal[1]
q = varfinal[2]

print(varfinal)
#sales plot (pdf)
#time interpolation
tp=(np.linspace(1.0, 100.0, num=100))/10
cofactor= np.exp(-(p+q) * tp)
sales_pdf= m* (((p+q)**2/p)*cofactor)/(1+(q/p)*cofactor)**2
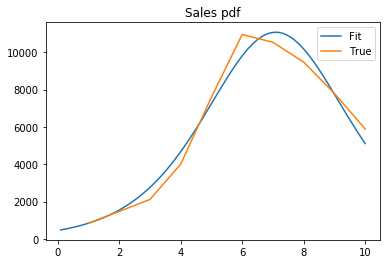
plt.plot(tp, sales_pdf,t,sales)
plt.title('Sales pdf')
plt.legend(['Fit', 'True'])
plt.show()

ソースコード出典:[2]

参考URL
[1]Chapter 15 Product Market Forecasting using the Bass Model
[2]github

2-2-11. 指数平滑化モデル

最新のデータほど大きな重みを、古いデータほど小さい重みをかけて、移動平均を取る方法。
最新のデータほど現在は未来に対して大きな意味を持っている、と考えることを前提にしている。
考慮するデータの種別に応じて、1次から3次まである。

1次の場合
y(t) = alpha x y(t-1)(実績値) +　alpha x y(t-1)(予測値)
１ステップ前に重みを置く。
alphaは、任意で設定する。大きい値ほど直前の値を重視する。
2次の場合
1次のy(t)という「観測値とこれまでの予測値の重み付き和」を”レベル”と呼び、
一度の観測でレベルがどれだけ変化したか、つまりレベルの差を”最新のトレンド”とみなし、
（次のトレンド）=beta x (最新のトレンド) + (1-beta) x　(これまでのトレンド)
　(予測値) = (レベル) + (次のトレンド)
で表す。
3次（別名Holt-Wintersモデル)
2次の場合に、今度は季節周期性を設定し、予測値を出す手法。
季節性成分の初期値は、任意に設定する。
(nステップ目の季節性成分) = gamma * (nステップ目の初期季節性成分 - レベル) + (1-gamma) * (nステップ目の季節性成分)
から
(予測値) = (レベル) + (周期のnステップ目) * (トレンド) + （n-1ステップ目の季節性成分）
と算出する。

参考：淺田　他著、”在庫管理のための需要予測入門”、２００７年
参考URL:
1.JMP、"平滑化法モデルの統計的詳細"
2.takuti.me、"異常検知のための未来予測：オウム返し的手法からHolt-Winters Methodまで"

2-2-12. 状態空間モデル

観測したいデータを”状態方程式”として、実際に計測できるデータを”観測方程式”として２つに分けて、計測誤差などがあることを考慮して予測を行うモデル。
欠損値がある場合や、非定常の場合にも適用できる、応用範囲の広いモデル。

また、状態ノイズや観測ノイズが非ガウス型分布の場合を特に、
”非ガウス型状態空間モデル”と呼ぶ。

適用するフィルタや手法により、複数種類ある。
今回は、解析対象のデータの種別に基づき、分類を行う。

a) 単純なデータ（線形、ガウス型分布）にのみ適用可能
- カルマンフィルタ
- 拡張カルマンフィルタ

b) 複雑なデータ（非線形、非ガウス型分布）にも適用できる手法
- 粒子フィルタ
- ギブスサンプラー
- ハミルトニアンモンテカルロ法

参考URL:
1.Logic of Blue、"状態空間モデルの推定方法の分類"

カルマンフィルタ
状態空間モデルの状態方程式に、補正項を加えることで精度を上げる手法。
補正後の状態　＝　補正前の状態＋カルマンゲイン×（本物の観測値－予測された観測値）
1.Logic of Blue、"状態空間モデル"
拡張カルマンフィルタ
アポロ計画でも使われた。
カルマンフィルタにおける観測・状態の記述が非線形の場合に適用。
1.大橋耕也、"カルマンフィルタ（ローカルレベルモデル）"
粒子フィルタ
・状態が”過去の状態”から確率的に定まり、かつ観測値も状態から確率的に定まるケースに適用できる。
　状態、及び観測値のどちらも、条件付き確率分布からリサンプリングされる。
　条件付き確率分布を算出するために、モンテカルロ法を用いることが多い。
1.データ分析関連のまとめ、"状態空間モデル(粒子フィルタ)"
MCMC法
粒子フィルタと同様、分布をたくさんの乱数で近似しますが、粒子フィルタが逐次的に予測 → フィルタリングを繰り返すのに対し、MCMCは初めから全時点のデータを使って分布を近似します。そのため平滑化分布のみが計算され、予測分布を得るには追加の計算が必要になる。
参考URL
1.AVILEN、"時系列データ解析における状態空間モデルの枠組み"
2."MCMC チュートリアル入門から多峰性分布の扱いとその応用まで"
ギブスサンプラー
条件付き分布から順番に生成した乱数の収束先は、無条件分布から生成した乱数に等しくなるという性質を利用した乱数生成法。MCMC（マルコフ連鎖モンテカルロ）法の一種。
参考URL
1.biostatistics、"ギブス・サンプリング"
2."MCMC法とその確率的ボラティリティ変動モデルへの応用"
3."http://www2.econ.osaka-u.ac.jp/~tanizaki/cv/papers/chap20.pdf"
4.谷崎久志、"非線形・非正規状態空間モデルの推定について"
ハミルトニアンモンテカルロ法
MCMC法の一種。物理空間上を、ハミルトニアンが一定であるという制約を満たすような移動を複数ステップ繰り返しながらサンプリングを行う手法。
参考URL
1.bioinfomatics、"ハミルトニアンモンテカルロアルゴリズム"

2-2-13.RNNモデル

いわゆる深層学習モデルの一種。
入力層、中間層、出力層のうち、中間層に繰り返し構造を持ち、
t=1,2・・・t’までの情報を持つことで、
t=t’+1の推論を行う。

参考URL
1."再帰型ニューラルネットワークの「基礎の基礎」を理解する　～ディープラーニング入門｜第3回"

2-2-14.LSTMモデル

RNNでは、勾配焼失によって、遠い過去のデータを推論に使うことができないという課題がある。
LSTMでは、LSTMブロックという単位で、勾配消失を回避し、過去データも推論に使えるようにしている。

参考URL
1.Qiita "LSTMネットワークの概要"
2.sagantaf "RNNとLSTMを理解する"

2-2-15.カオス解析

ランダムなノイズがないにも関わらず、不規則な変動を示すデータのことを「カオス」と呼ぶ。このカオスな時系列データに対して、過去のデータと写像関係があるものと仮定して、立式するモデル。
ロジスティック写像などが有名。

参考URL
1.Logic of Blue、"カオス時系列の基礎とニューラルネットワーク"
2.池口徹、"カオスと時系列解析"

2-2-16.確率的ボラティリティモデル

ARモデルからSARIMAモデルで、誤差項は独立かつ同一の分布に従うとしていた。
しかし、不祥事発覚などのように、大きな変動が局所的に現れる現象が起きたときに、
直後からしばらくの間変動が続くことを説明するために、誤差高の分散に時系列構造を導入するモデル。

参考URL
1.北川源四郎他、"非ガウス型状態空間表現による
確率的ボラティリティモデルの推定"
2.AVILEN、"時系列データを解析するための様々なモデル"

2-2-17.レジームスイッチングモデル

別名:マルコフ自己回帰モデル
データの裏側に離散的な状態があり、その状態（＝レジーム）によってモデルが変化するモデルのこと。
状態の種類によって、以下の２種類にカテゴリ化できる。

a)状態が観測可能な変数
- 閾値モデル
- 平滑推移モデル

b)状態が観測不可能な変数
- マルコフ・スイッチングモデル
- 時変推移確率モデル

参考URL
1.長倉大輔、"レジーム・スウィッチングモデル"
2.沖本竜義、"マルコフスイッチングモデルの
マクロ経済・ファイナンスへの応用"
3.AVILEN、"時系列データを解析するための様々なモデル"

3.ライブラリ

業務ではPython3を使っているため、時系列データ解析に使えるPythonのライブラリを以下に挙げる。

3-1.statsmodels

万能。幅広い手法も使えるし、各種パラメータやモデルの性能（AICなど）も出力できる。
1.公式ページ

3-2.prophet

Facebook謹製のライブラリ。予測結果はすぐに出せるが、statsmodelsのようにモデル性能などを出力できない。初心者向けか。
1.公式ページ

3-3.pyFlux

stasmodelsと仕様は似ている。グラフ描画機能もあって、使いやすそう。
1.github "RJT1990/pyflux"
2.Qiita "時系列データの予測ライブラリ--PyFlux--"

4.まとめ（所感）

技術マップを作成するにあたり、四苦八苦した点を以下に挙げる。
・線形・非線形に明示的に言及していない資料が多い。（常識だからか？）
・自己回帰、状態空間、深層学習（RNNやLSTM）は、ネット上に日本語資料が大量にあるが、ベイジアン動的線形やマルコフスイッチモデル、カオス解析、ECM(Error Correct Model)は用語を知らないとGoogle先生がなかなか答えてくれない。（”時系列”、”カオス解析”と２つのワードを入力すると、きちんと答えてくれる）
・TJO先生、Logics of Blue、統計数理研究所のHPは神。
・非定常の手法は、そもそも名前を見つけるのに苦労した（例：カオス解析）。時系列データ解析の専門家の人には、ぜひ技術マップを作成して欲しいと思ってしまった。（ガウス型、非ガウス型の観点での分類はよくある。）

　変更履歴

2021年04月04日v1 Bassモデルの理論式と実装例・outputを追記。
2021年04月04日v0 MA,ARMA,ARIMA,VARモデルの実装例とoutputを追記。
2021年01月31日リンク先の表記方法を修正・深層学習の記載を見直し。ARモデルの実装例(python3)を追記。
2020年08月16日状態空間モデル、深層学習　など説明追加

【時系列】時系列データ予測 予測手法マップ

1.本記事作成の背景

2.技術マップ（モデルマップ）

2-1. マップ総論

2-2. モデル別概要

2-2-1. 総論

2-2-2. 自己回帰モデル

2-2-3. 移動平均モデル

2-2-4. 自己回帰移動平均モデル

2-2-5.自己回帰和分移動平均モデル

2-2-6. 季節性自己回帰和分移動平均モデル

2-2-7.ベクトル自己回帰モデル

2-2-8. 構造ベクトル自己回帰モデル

2-2-9. ベイジアン・ベクトル自己回帰

2-2-10. Bassモデル

2-2-11. 指数平滑化モデル

2-2-12. 状態空間モデル

2-2-13.RNNモデル

2-2-14.LSTMモデル

2-2-15.カオス解析

2-2-16.確率的ボラティリティモデル

2-2-17.レジームスイッチングモデル

3.ライブラリ

3-1.statsmodels

3-2.prophet

3-3.pyFlux

4.まとめ（所感）

変更履歴

【時系列】時系列データ予測　予測手法マップ

　変更履歴