概要
わたしはQiitadonというmastodon(TwitterライクなOSSのSNS)でtootしていますが、少しtootの数が多くなってきたので、自分がbotではないか少し不安になってきました。
そこで、ベンフォードの法則を用いて自分が人間である事を示します。
実際にやることは、(Pythonを用いて)
- tootの取得
- 時間隔の取得
- $\chi ^2$検定によってベンフォードの法則に従うか否かの判定
- (おまけ:その他の内容の取得)
です。はやく人間になりたい
特に
- $\chi ^2$検定を実際にどのように使うのかという具体例
- 意識していない人間の自然な振る舞いが、実はきれいに統計的な法則に当てはまることの驚き
みたいなものを感じてもらえると嬉しい記事です。
ベンフォードの法則とは
さて、ベンフォードの法則とは、ある適当な数値の最上位の桁の数が、次のような分布に従うことを主張する"法則"です。
主張:その数値を測定したときの最上位の桁の数が$n$である確率は、$\log_{10}(n+1) - \log_{10}(n)$である。
この「ある適当な数値」というのが何か?という事まではベンフォードの法則では主張をしておらず、物理法則のようなものとして解釈しようとするとある意味で片手落ちですが、ここでいう法則というのは80:20の法則(パレートの法則)のような意味として捉えます。
これは、ある種の数値に対しては明らかに成立しない法則です。例えば、IQの分布を考えてみると、IQというのは100を基準として、±15または±10のところに全体の約8割がおさまるような正規分布に近い分布になっているので、2や3で始まるIQはほとんどありえず、通常のスケールに従う限りはこの主張を満たすことはありません。
しかし、様々な測定値に対して成立することが知られていて、その"理由"としてもいくつかの根拠が挙げられています。あまり詳しくは触れませんが、ここでは、Wikipediaに書いてある対数スケールにおける分布幅の説明と本質的に同じですが、少し違う言い方での説明を末尾に記載しておきます。
tweetの間隔とベンフォードの法則に関する示唆
人間がtweetをした場合に、ベンフォードの法則にあてはまるということへの示唆は、
ベンフォードの法則を応用したbotアカウント検出などにあります。
この論文で扱っているのは、tweet間隔と単語数を人間とbotの分類において利用するという事ですが、これはmastodon(qiitadon)でも通用するはずです。早速検証してみましょう。
私は人間であると信じたい。
tootの取得
Qiitadonから自分のtootを取得します。本当はAPIを使った方が良いですが、多分こんな事をやる人は自分ぐらいなのと、APIに合わせた通信仕様にすると少し時間がかかるので、適当な取得の仕方をします。
これは単に標準出力に垂れ流すだけのスクリプトなので、$ python3 get_toot.py > tootlog.csvなどとします。
import urllib
from bs4 import BeautifulSoup
name = 'sasanquaneuf'
url = 'https://qiitadon.com/@' + name
while url:
req = urllib.request.Request(url)
with urllib.request.urlopen(req) as response:
html = response.read().decode("utf-8")
soup = BeautifulSoup(html)
display_names = [s.find('span') for s in soup.find_all(class_='display-name')]
contents = soup.find_all(class_='status__content')
toot_times = soup.find_all('time')
for display_name, content, toot_time in zip(display_names, contents, toot_times):
if str(display_name).find(name) == -1:
continue
print(toot_time.attrs['datetime'] + ',' + content.text)
older = soup.find('a', class_='older')
url = older.attrs['href'] if older else None
時間隔の取得(など)
本当は取得するタイミングでやればよいのですが、一度上記のようにしてデータを取得してから、その取得したデータを処理する形で実装します。
ここで、単にベンフォードの法則の検証をするだけならMeCab等は必要無いのですが、ついでに他の分析をするためにMeCabで分割処理します。以下、Jupyter notebookのセルを抽出しているので、少しずつコード断片を示します。
※MeCab, pandas, seabornを使います。
import MeCab
mecab = MeCab.Tagger ('-d /usr/local/lib/mecab/dic/mecab-ipadic-neologd')
# なぜかparseToNodeのsurfaceがうまく動かなかったので、手製で雑な処理
def tokenize(japanese):
for s in mecab.parse(japanese).split('\n'):
token = s.split('\t')
if len(token) > 1:
feature = token[1].split(',')
yield token[0], feature[0], feature[1], feature[5], feature[6]
from datetime import datetime
import re
with open('tootlog.csv') as f:
lines = f.readlines()
lines.sort()
results = []
prev_line = ''
prev = datetime.strptime(lines[0][:20], '%Y-%m-%dT%H:%M:%SZ')
for line in lines:
if prev_line == line:
continue
prev_line = line
text = re.sub('https?://[\\x20-\\x7E]+', 'URL', line[21:-1])
toot_date = datetime.strptime(line[:20], '%Y-%m-%dT%H:%M:%SZ')
token = list(tokenize(text))
rag = toot_date - prev
prev = toot_date
results.append((text, toot_date, token, rag))
import pandas as pd
import seaborn as sns
df_summary = pd.DataFrame(results, columns=['toot', 'time', 'token', 'rag'])
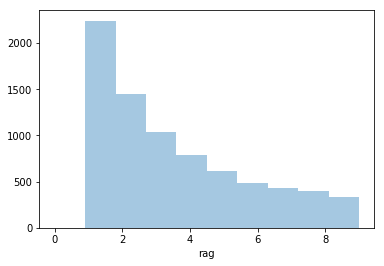
sns.distplot(df_summary['rag'].apply(
lambda x: int(str(x.total_seconds())[:1])), kde=False, rug=False, bins=10)
結果、次のようなグラフを得ます。
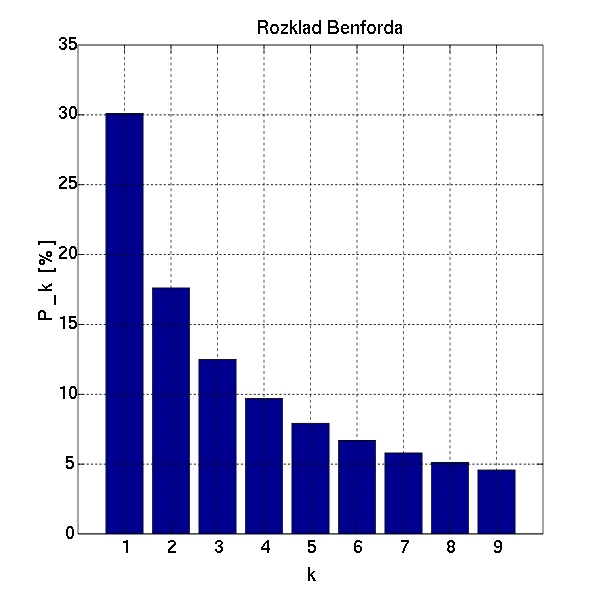
これを、Wikipediaのグラフと比較してみましょう。
おー、だいぶそれっぽい!わたしにんげん!
と思いたいところですが、本当に私のtootがベンフォードの法則に従っているかどうか、検定します。
χ2乗検定
ある分布が得られた時、その分布が本当に期待する分布によって得られたものと思ってよいかどうか?を検証するには、一般に$\chi^2$検定が用いられます。
今回の場合は、1,2,3,...,9のうちどれが出るか?という確率についての検定なので、自由度は8です。
import math
df_summary['first_digit'] = df_summary['rag'].apply(
lambda x: int(str(x.total_seconds())[:1]))
first_digit = df_summary[
(df_summary['first_digit'] != 0)
].groupby('first_digit').count().reset_index()[['first_digit', 'time']]
first_digit['expected'] = [
sum(first_digit['time']) * (math.log(i + 1, 10) - math.log(i, 10)) for i in range(1, 10)]
sum([(row['time'] - row['expected']) ** 2 / row['expected'] for _, row in first_digit.iterrows()])
私のデータでこれをやると、
20.818077578456744
となりました。
さて、これを数表で見てみると…あれあれ…
自由度8の0.01を超えてしまいました。つまり、これよりも稀な事象(雑)が起こる確率は、0.01よりも小さいということです。普通は、仮説(今回の場合は、私がベンフォードの法則に従う人間であるという説)が棄却されてしまいます。
わたし、やっぱりbotだった?
χ2乗検定(不都合なデータを除く)
botじゃないと信じたいので、結果を捏造します考察をします。
これ、first_digitを出力してみると、以下のようになっています。
| first_digit | time | expected |
|---|---|---|
| 1 | 2242 | 2339.003066 |
| 2 | 1449 | 1368.229083 |
| 3 | 1036 | 970.773983 |
| 4 | 790 | 752.990801 |
| 5 | 611 | 615.238282 |
| 6 | 481 | 520.176555 |
| 7 | 427 | 450.597428 |
| 8 | 402 | 397.455099 |
| 9 | 332 | 355.535702 |
2と3が特に多いのですが、これは多分わたしの睡眠時間と関係していて、睡眠時間を仮に6時間とすると6*3600とかなので、多分ちょうどそれぐらい間が空いてからのtootが多いということなんですよね。
そういう不都合なデータを、一旦取り除いてみます。具体的には、20000秒よりも大きい時間隔を取り除きます。
df_summary['first_digit'] = df_summary['rag'].apply(lambda x: int(str(x.total_seconds())[:1]))
first_digit = df_summary[
(df_summary['first_digit'] != 0) & (df_summary['rag'].apply(lambda x: x.total_seconds() < 20000))
].groupby('first_digit').count().reset_index()[['first_digit', 'time']]
first_digit['expected'] = [
sum(first_digit['time']) * (math.log(i + 1, 10) - math.log(i, 10)) for i in range(1, 10)]
sum([(row['time'] - row['expected']) ** 2 / row['expected'] for _, row in first_digit.iterrows()])
こうすると、
10.84876218655414
という事になり、これを数表と見比べると、10%よりもずっとベンフォードの法則に従う、人間っぽい存在ということになります。ちなみに、first_digitの出力結果は以下のようになります。
| first_digit | time | expected |
|---|---|---|
| 1 | 2241 | 2206.248838 |
| 2 | 1203 | 1290.572838 |
| 3 | 916 | 915.676001 |
| 4 | 750 | 710.253485 |
| 5 | 594 | 580.319352 |
| 6 | 474 | 490.653021 |
| 7 | 424 | 425.022979 |
| 8 | 396 | 374.896837 |
| 9 | 331 | 335.356648 |
よかった!わたしにんげん!
2と3の差分が合計で366なので、私のtoot期間が10ヶ月強であることを考慮すると、だいたい睡眠時間仮説があたっているように思えます。
おまけ1:自分のデータ
文字数、単語数、頻繁に使用する単語の一覧を出力してみます。
文字数/単語数に対するベンフォードの法則の検証は、あまりうまくいきませんでした。結果概要と、グラフのみ示します。
結果概要
| 種類 | 条件 | $\chi^2$ |
|---|---|---|
| 文字数 | 条件なし | 76.77223504995722 |
| 文字数 | 450未満 | 68.55413241962368 |
| 単語数 | 条件なし | 46.839316729341384 |
| 単語数 | 100未満 | 194.82841003453063 |
| 単語数 | 名詞のみ | 83.66646018374638 |
わたし人間じゃないベンフォードの法則っぽい分布にはなっても、厳密にはそうなっていないということですね…
この辺は若干の調整が必要です。
文字数
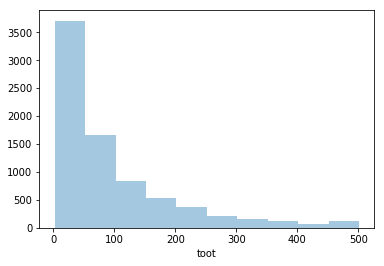
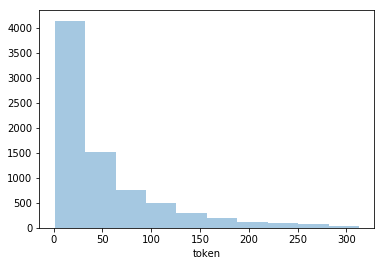
sns.distplot(df_summary['toot'].apply(lambda x: len(x)), kde=False, rug=False, bins=10)
tootは500文字までできますが、分布は指数的な感じですね。
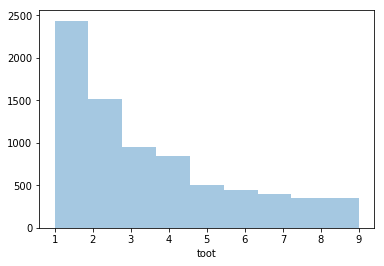
上1桁を取ると次のようになります。500で頭打ちになっている影響がよくわかります。(4が多く5が少ない)
sns.distplot(df_summary['toot'].apply(lambda x: int(str(len(x))[:1])), kde=False, rug=False, bins=9)
単語数
文字数のかわりに、日本語の単語数だと以下のようになります。
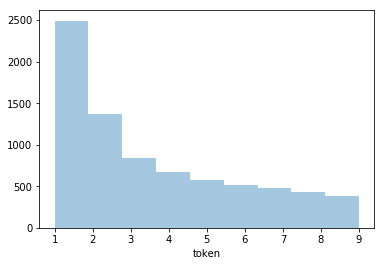
sns.distplot(df_summary['token'].apply(lambda x: len(x)), kde=False, rug=False, bins=10)
露骨な頭打ちが消えました。
sns.distplot(df_summary['token'].apply(lambda x: int(str(len(x))[:1])), kde=False, rug=False, bins=9)
頻繁に使用する単語
一部の変な単語などを除いた上で、よく使用する単語を抽出してみます。
tokens = []
for r in results:
tokens += [(r[1], x) for x in r[2]]
df = pd.DataFrame(tokens, columns=['time', 'token'])
high_use_word = df[df['token'].apply(
lambda x: x[0] not in ('URL', '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', '一', 'ー') and
x[1] in ('名詞', '形容詞') and x[2] not in ('非自立', '代名詞', '接尾')
)].groupby('token').count().sort_values(by='time', ascending=False).reset_index()
high_use_word['token'].apply(lambda x: x[0])[:50]
人 ない 自分 場合 仕事 感じ 話 良い 意味 問題
必要 会社 なく コード 理解 今 多い いい 前 記事
時間 難しい 無い 処理 つらい 普通 日本 部分 一番 データ
Qiita 開発 作業 昔 レベル 今日 技術 結果 対応 システム
人間 気 最近 関数 失敗 バグ 環境 方法 テスト 機能
となりました。それっぽい!わたしかいはつにんげん!
むすび
人間である事が証明できました。多分。
この記事でわかったことは、
- tootの時間隔を秒数で表記すると、だいたいベンフォードの法則に従う
- ただし、睡眠時間などの要因によって、見た目それっぽくても$\chi^2$検定をすると仮説が棄却される可能性はある
- 真の人間になるには睡眠中もtootする必要がある
真の人間になる道のりは、まだ長い―
以下、おまけです。
おまけ2:他のbotだったかもしれない人のデータ
時間隔のデータは以下のようになりました。
| 名前 | 全て | <20000のみ |
|---|---|---|
| A氏 | 27.043940248094742 | 12.668263437972598 |
| B氏 | 10.250977179448498 | 11.581251123074292 |
| C氏 | 19.58828967298915 | 11.481344670811652 |
みんなbotではなさそうですね。よかった、botなんていなかったんや!
ちなみに、どの人も文字数や単語数は微妙な感じでした。
おまけ3:どのような背景でベンフォードの法則が成り立つのか、一つの説明
その数値の分布が、多くの桁をまたぐような分布であるとき、例えば、ある数値が1から1000000まで、(1)1の場合も(2)10~19の場合も(3)100~199の場合も(4)1000~1999の場合も(5)10000~19999の場合も(6)100000~199999の場合も概ね同数分布していて、かつある程度連続的な分布を考えてみます。
すると、その分布の密度は、数値の増加に対して反比例で減少していくことになります。
(1桁では1個,2桁では10~19の10個,3桁では100~199の100個,...ということです)
このとき、各桁の出現率を計算しようとすると、つまり反比例のグラフの積分となるので、例えば最上位が1:最上位が2というのは適当な定数$c$について
$$\int_1^2 \frac{c}{x}dx : \int_2^3 \frac{c}{x}dx \ = \ \int_1^2 \frac{1}{x}dx : \int_2^3 \frac{1}{x}dx$$
ということになります。これが1から9まで全ての整数について言えることと、$\log_{10}10 = 1$であることから、主張の式が成り立つことになります。
一般に、各分布がそれぞれ概ね同数でなかったとしても、例えば1~9の分布がだいたい均一、10~99の分布がだいたい均一、...という事が言えるような"なだらかな"分布である場合などは、ざっくりと同じ法則が成り立つことになります。
特に、小さいスケールと大きいスケールで従う法則が異なる(確率分布が異なる)場合で、いくつかの確率分布からランダムに抽出をするような場合にも、ベンフォードの法則に従う場合がある事がわかっています。