はじめに
散乱界FDTD法と呼ばれる数値計算法を用いて,
測定(を模擬した手法)によって得た電界が,
人体(っぽいモノ)にどのように吸収されるか見てみましょう。
背景
皆さんは電磁界の数値計算やってますか?
***「あ~~~~波源のモデル化めんどいし, ここまで来たら実測値使ったほうがはえ~~~~~~わ!!」***って思ったことないですか?
もしくは, ***「自由空間の電界分布は分かるのに, 散乱体入れたらどうなっちゃうの~~~!?」***ってことはないですか?
どちらもよくありますね。
実例としては, 「ブラックボックス化された波源近くに立つ人体が, どれくらい電磁界を浴びるか」といった話です。
ブラックボックス化された波源はモデル化できないし, 人体の中の電磁界を直接測ることもできません。
ここでは, 上記の実例問題の簡略化として, 「実験測定っぽい電界の中に, 人体っぽい物を置いたときの電磁界解析」を行います。
手法概略
PureなFDTD法
単純なFDTD法については, 過去の記事を参照いただけると幸いです。
数値計算に親しむ ~FDTD法による電磁界解析編 (1)概要と基礎実践~
https://qiita.com/sandshiP/items/f07f6c1443e024cb775a
数値計算に親しむ ~FDTD法による電磁界解析編 (2)3次元への拡張とアンテナ放射解析~
https://qiita.com/sandshiP/items/27bc6ee6f079a88b0f08
数値計算に親しむ ~FDTD法による電磁界解析編(3) FFTを用いたアンテナの周波数特性解析~
https://qiita.com/sandshiP/items/2b8b10265d0c11597081
すごく大雑把にに説明すると, 波源・散乱体を計算空間に入れ, 電磁界を空間的・時間的に差分化して解く方法です。
特徴としては, 差分化モデル化するため波源・散乱体の内部構造が明らかとなっている必要があり, また計算空間が大きくなると計算が辛くなってきます。
PureなFDTD法を使ううえで, 辛い問題の事例としては, 波源が非常に詳細な構造をしており, 空間分解能を上げる必要がある場合です。
例としては, スマートフォンの近くにいる人体, とかでしょうか。
スマートフォンの内部構造は極めて微細な構造(~1 mm以下), 人体は約1.8 m程度のスケールを持っているため, 計算空間は$1800 \times 400 \times 300$セルくらいになってしまう場合もあります。
そういった問題に対しては, 実際にスマートフォン周りの電界を測ってしまって, 何らかの方法で人体内部の電磁界を計算してしまったほうがよい場合もあります。
散乱界FDTD法概要
波源のモデル化が困難な場合の, 数値計算手法としてはいろいろなものがあります。
通常は, 対象とする周波数とか問題のサイズ等で決定しますが, ここでは散乱界FDTD法を使います。
散乱界FDTD法は, 散乱界のみを計算するFDTD法です。
そもそも電磁界は, 散乱界と入射界に分離可能であり, またそれぞれを独立して考えることができます。
そのため, 入射界は既知のもの(測定値等)を用い, 散乱界のみをFDTD法で計算してしまおう, という考え方です。
実際に式を追いかけてみます。
以下, 全電磁界を$\boldsymbol{E}^t, \boldsymbol{H}^t$, 入射界を$\boldsymbol{E}^{inc}, \boldsymbol{H}^{inc}$, 散乱界を$\boldsymbol{E}^{scat}, \boldsymbol{H}^{scat}$とします。
はじめに, 全電磁界は, 散乱界と入射界の和から成るため,
\begin{aligned}
\boldsymbol{E}^t & = \boldsymbol{E}^{inc} + \boldsymbol{E}^{scat} &…(1)\\
\boldsymbol{H}^t & = \boldsymbol{H}^{inc} + \boldsymbol{H}^{scat} &…(2)\\
\end{aligned}
がそれぞれ成り立ちます。
また, 散乱体($\epsilon, \mu$)内部における全電磁界$\boldsymbol{E}^{t}, \boldsymbol{H}^{t}$については, それぞれマクスウェルの方程式を満たすため,
\begin{aligned}
\nabla \times \boldsymbol{E}^{t} &= -\mu \frac{\partial \boldsymbol{H}^{t}}{\partial t} &…(3)\\
\nabla \times \boldsymbol{H}^{t} &= \sigma\boldsymbol{E}^{t} + \epsilon \frac{\partial \boldsymbol{E}^{t}}{\partial t} &…(4)
\end{aligned}
もそれぞれ成り立ちます。
式$(1)-(2)$を用いて, 式$(3)-(4)$を変形し,
\begin{aligned}
\nabla \times (\boldsymbol{E}^{inc} + \boldsymbol{E}^{scat}) &= -\mu \frac{\partial (\boldsymbol{H}^{inc} + \boldsymbol{H}^{scat})}{\partial t} \\\
\Leftrightarrow \mu \frac{\boldsymbol{H}^{scat}}{\partial t} &= -\nabla \times \boldsymbol{E}^{scat} - (\nabla \times \boldsymbol{E}^{inc} + \mu \frac{\boldsymbol{H}^{inc}}{\partial t})\\
\nabla \times (\boldsymbol{H}^{inc} + \boldsymbol{H}^{scat}) &= \sigma(\boldsymbol{E}^{inc} + \boldsymbol{E}^{scat}) + \epsilon \frac{\partial (\boldsymbol{E}^{inc} + \boldsymbol{E}^{scat})}{\partial t} \\
\Leftrightarrow \epsilon \frac{\boldsymbol{E}^{scat}}{\partial t} &= -\sigma \boldsymbol{E}^{scat} + \nabla \times \boldsymbol{H}^{scat} - (\sigma \boldsymbol{E}^{inc} + \nabla \times \boldsymbol{H}^{inc} + \epsilon\frac{\boldsymbol{E}^{inc}}{\partial t})
\end{aligned}
ここで, 入射界は波源の存在によらず常に一定(既知)でなければならないため, 式$(3)-(4)$における($\epsilon=\epsilon_0, \mu=\mu_0, \sigma=0$)としたときに等しく, 上式に代入します。
\begin{aligned}
\mu \frac{\boldsymbol{H}^{scat}}{\partial t} &= -\nabla \times \boldsymbol{E}^{scat} - (\mu - \mu_0)\frac{\boldsymbol{H}^{inc}}{\partial t} &…(5)\\
\epsilon \frac{\boldsymbol{E}^{scat}}{\partial t} &= -\sigma \boldsymbol{E}^{scat} + \nabla \times \boldsymbol{H}^{scat} - (\sigma \boldsymbol{E}^{inc} + (\epsilon - \epsilon_0)\frac{\boldsymbol{E}^{inc}}{\partial t}) &…(6)
\end{aligned}
上記式$(5)-(6)$および既知の入射界$\boldsymbol{E}^{inc}, \boldsymbol{H}^{inc}$を用いて, 散乱界$\boldsymbol{E}^{scat}, \boldsymbol{H}^{scat}$を, 時間領域で解き, その後入射界・散乱界から全電磁界を求めることで全電磁界を得ます。
計算結果
実装はFortranを使って行いました。
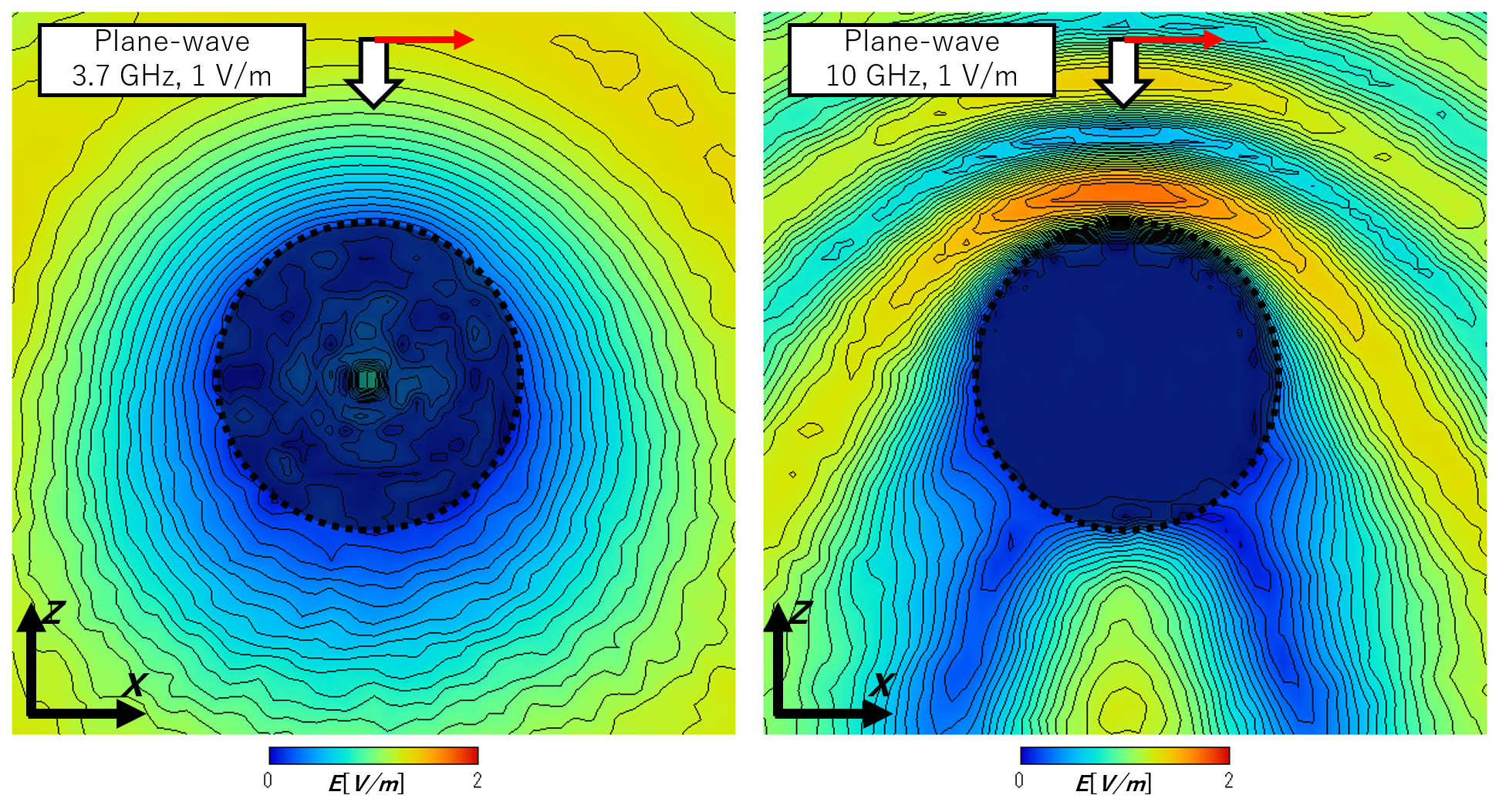
計算モデルは以下図のような、人体を模擬した均質誘電体(5 GHzにおける血液の電気定数, $\epsilon_r=53.95, \sigma=5.40$ [S/m]参考: IFAC-CNR, Florence (Italy), "Dielectric Properties of Body Tissues", 1997-2018.)に, $z$方向に伝搬する平面波を入射させています。
平面波としては, 測定による不確かさを大雑把に考慮して, 振幅の5%を雑音として与えており, 周波数は3.7 GHz, 10.0 GHzとしています。
実際この程度の問題であれば、普通のFDTD法で解くほうが速いし楽です。
あくまで、ここでは手法の紹介のみに留めさせてください。(厳密なことを言えば、ここまで高い周波数では透磁率云々を考える必要もあるし、今回の手法のみではあまり正確な結果は得られません。)
ただ、FDTD法以外の方法で得た入射界を使って、FDTD法で誘電体内部の電磁界を計算できることに、良さを感じていただけると嬉しいです。
誘電体球は点線で示した円の内側にあります。
誘電体球から上部(入射側)では電界が比較的強く、下部(遮蔽側)では電界が弱いように見えますね。
また、人体内部においては、10 GHzより3.7 GHzの電界のほうが深く入射しているように見えます。
なんとなく定性的なイメージともあっているので、計算もうまくできていそうですね。
まとめ
今回は、別に用意した入射界を用いて、FDTD法を解くことができることを示すため、「実験測定で得た電界の中に, 人体を置いたときの電磁界解析」を行いました。
まあ実際は、測定で得てもなければ人体でもないんですが。
ただ、FDTD法は、こういった測定と数値解析の搦め手によって、より広い範囲の問題を解くことができる極めて汎用的な手法である、ということはアピールできたと思います。
実装も簡単、理解も比較的しやすく、拡張性も高い、そんなFDTD法を使って数値解析を気軽に楽しみましょう。
参考
[1]宇野亨, 何一偉, 有馬卓司, "数値電磁界解析のためのFDTD法- 基礎と実践", コロナ社, 2016