数値計算に親しむ ～FDTD法による電磁界解析編(3) FFTを用いたアンテナの周波数特性解析～

はじめに

今回も楽しい数値計算をやります。

今回からは、前回までで作った3次元FDTD法を用いて、さらに実用に近い問題である、アンテナ入力特性解析を実装します。具体的には、アンテナにどれくらいの周波数を入れれば最も効率が良いか、数値計算で求めてみましょう。

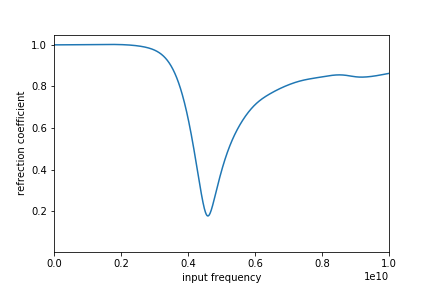
今回の結果としては、こんな感じの反射係数のグラフを求めます。この結果からは、対象のアンテナには4.0 GHzの入力を入れると反射が少なく効率が良さそう、とわかります。
ちなみに、本解析結果は、後述する事情によりかなり精度が悪いです。

[前回]数値計算に親しむ　～FDTD法による電磁界解析編 (2)3次元への拡張とアンテナ放射解析～
https://qiita.com/sandshiP/items/27bc6ee6f079a88b0f08

[初回]数値計算に親しむ　～FDTD法による電磁界解析編 (1)概要と基礎実践～
https://qiita.com/sandshiP/items/f07f6c1443e024cb775a

今回も、詳細な理論等は端折りつつ、概要のみの説明となります。

前回の3次元FDTD法の拡張

今回は、前回使用した3次元FDTD法に、いくつか機能を追加して、対象とする問題を解きたいと思います。

前回、電磁界の計算に使用したコードはこちら。
併せて、今回新たに機能を追加する要件を、課題としてコード中に示しています。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

dx = 0.01 # x方向空間差分間隔[m]
dy = 0.01 # y方向空間差分間隔[m]
dz = 0.01 # z方向空間差分間隔[m]

c = 2.99792458e8 # 光速[m/s]

dt = 0.99/(c * np.sqrt((1.0/dx ** 2 + 1.0/dy ** 2 + 1.0/dz ** 2))) # 時間差分間隔[s] c.f.Courantの安定条件
f = 1.0e9 # 周波数[Hz]

nx = 100 # x方向計算点数
ny = 100 # y方向計算点数
nz = 100 # z方向計算点数

nt = 250 # 計算ステップ数

# 電気定数初期化と更新係数の計算
eps = np.full((nx, ny, nz), 8.854187817e-12)
mu = np.full((nx, ny, nz), 1.2566370614e-6)
sigma = np.full((nx, ny, nz), 0.0)

#############################
#課題(1) 吸収境界条件の設定
#############################

dhx = dt / (mu * dx) # 式(9) - (11)の右辺係数
dhy = dt / (mu * dy) # 式(9) - (11)の右辺係数
dhz = dt / (mu * dz) # 式(9) - (11)の右辺係数

ce = 1.0 - dt * sigma / eps # 式(12) - (14)の右辺第一項係数
dex = dt / (eps * dx) # 式(12) - (14)の右辺第二項係数
dey = dt / (eps * dy) # 式(12) - (14)の右辺第二項係数
dez = dt / (eps * dz) # 式(12) - (14)の右辺第二項係数

# 電磁界初期化
t = 0.0

E_x = np.zeros(shape=(nx, ny, nz))
E_y = np.zeros(shape=(nx, ny, nz))
E_z = np.zeros(shape=(nx, ny, nz))
H_x = np.zeros(shape=(nx, ny, nz))
H_y = np.zeros(shape=(nx, ny, nz))
H_z = np.zeros(shape=(nx, ny, nz))

image_list = []
for _ in range(nt):

    # 電界のz成分を励振
    E_z[nx//2, ny//2, nz//2] = np.sin(2.0 * np.pi * f * t)

    t += dt/2

    # 電界各成分計算
    E_x = ce * E_x + dez * (H_z - np.roll(H_z, shift=1, axis=1))\
                   - dey * (H_y - np.roll(H_y, shift=1, axis=2))

    E_y = ce * E_y + dey * (H_x - np.roll(H_x, shift=1, axis=2))\
                   - dez * (H_z - np.roll(H_z, shift=1, axis=0))

    E_z = ce * E_z + dez * (H_y - np.roll(H_y, shift=1, axis=0))\
                   - dex * (H_x - np.roll(H_x, shift=1, axis=1))

    E_amp = np.sqrt(E_x ** 2 + E_y ** 2 + E_z ** 2)

    # 電界のz成分を励振
    E_z[nx//2, ny//2, nz//2] = np.sin(2.0 * np.pi * f * t)

    t += dt/2

    # 磁界各成分計算
    H_x = H_x + dhz * (E_z - np.roll(E_z, shift=-1, axis=1))\
              - dhy * (E_y - np.roll(E_y, shift=-1, axis=2))

    H_y = H_y + dhy * (E_x - np.roll(E_x, shift=-1, axis=2))\
              - dhz * (E_z - np.roll(E_z, shift=-1, axis=0))

    H_z = H_z + dhz * (E_y - np.roll(E_y, shift=-1, axis=0))\
              - dhx * (E_x - np.roll(E_x, shift=-1, axis=1))

    #############################
    #課題(2) アンテナ入力電流式を実装
    #############################


#############################
#課題(3) アンテナ入力特性解析を実装
#############################

かなりざっくりとですが、現状の課題は以下3つです。

1. 端面の吸収境界を実装
2. アンテナ入力電流を求める
3. アンテナ入力特性解析を実装

それでは、順に実装していきます。

1. 端面の吸収境界を実装

背景

前回も少しだけ述べましたが、何も処理を加えていない現在の端面の条件は、領域外のセルにおける電磁界はすべて$0$として扱っています。
電界の接線成分が常に$0$となる場合、その境界条件は全反射と等価であり、現在は計算領域がすべて金属で覆われている（厳密に言うと、接線成分以外も$0$とするため、現実にはありえない反射）条件となってしまいます。

一方で、今回解析したいのは、アンテナ単体の入力特性です。
アンテナがアンテナ以外からの影響を受けないような、無響室での解析をしたい…。
でも十分大きな計算空間を用意するには計算コストが莫大に必要…。

そこで、役に立つのが以下の、「吸収境界条件」です。

実装

吸収境界条件にはいくつか種類がありますが、ここではPML(Perfectly Matching Layer)境界条件についてごく簡単に説明します。

私達がいま求めたいのは、端面においてあたかも無限遠であると模擬できる、以下の境界条件です。

• 端面からの反射がない
• 入射した電磁界を減衰させる

このことから、計算領域と計算領域外が、完全にインピーダンス整合の取れた状態であり、あたかも連続面であるかのように模擬できるんじゃないか、っていう考え方がPML境界条件です。（省略しすぎてよくわからないですが、詳細は次回以降に記載します。）

実際に、式の導出・実装は非常に長くなってしまい、今回の本質から外れてしまうため、こちらも割愛します。

2. アンテナ入力電流式を実装

背景

本記事で最終的に求めたいアンテナの反射係数は、アンテナの入力インピーダンス、すなわち周波数特性を持つ抵抗値によって求められます。

アンテナの入力インピーダンス$Z$は周波数$f$および入力電流・入力電圧の周波数領域における複素数表現$\dot I, \dot V$の関数として、以下の式$(4)$で表されるため、$\dot I, \dot V$を求めればよいです。
$$
Z(f) = \frac{\dot V(f)}{\dot I(f)}　...(4)
$$

$\dot I(f), \dot V(f)$は、周波数領域の値ですから、時間領域の$I(t), V(t)$をフーリエ変換によって周波数領域に読み替えてあげればよいですね。

しかしながら、現在私達にとって既知の値は、入力電圧の時間領域における実数表現$V(t)$のみです。
ですので、入力電流の時間領域における実数表現$I(t)$を求めましょう。

実装

給電点においてアンテナ方向の$z$軸に沿って流れる電流は、周囲の$xy$平面上の磁界の周回積分によって求めることができます（アンペールの法則）。
よって、以下の式$(5)$を離散・差分化することで得られる式$(6)$を用いて計算できます。

\begin{aligned}
I &= \oint_{\partial S_{xy}} \boldsymbol{H} \cdot \mathrm{d} \boldsymbol{l}　&...(5)\\
I & = \Bigl(H_x(x, y-dy, z) - H_x(x, y, z)\Bigr)dy \\
  & + \Bigl(H_y(x, y, z) - H_y(x-dx, y, z)\Bigr)dx　&...(6)\\
\end{aligned}

こちらの電流に関する式を給電点[nx//2, ny//2, nz//2]周りで実装したのが以下のコードです。

Iin = dy * (H_x[nx//2, ny//2 - 1, nz//2] - H_x[nx//2, ny//2, nz//2])\
    + dx * (H_y[nx//2, ny//2, nz//2] - H_y[nx//2 - 1, ny//2, nz//2])

3. アンテナ入力特性解析を実装

実装

ここまでで、時間領域の電流・電圧$I(t), V(t)$を求めることができました。
では、高速フーリエ変換（FFT）によって周波数領域に読み替えて、$\dot I(f), \dot V(f)$を求めましょう。

FFTの詳細説明は省きますが、FFTによって時間領域の波形から、その波形がどんな周波数をどれくらいの強さ含んでいるか、を求めることができます。

先程で得た時間領域の電流・電圧$I(t), V(t)$に含まれる周波数成分を以下のコードで求めましょう。

vfreq = np.fft.fft(vtime)
ifreq = np.fft.fft(itime)
zfreq = vfreq/ifreq 

ここでは、numpyの機能を用いて極めて簡単に実装しました。
今や一瞬でFFTの実装・解析ができるんですね、強力です。

また、周波数領域の離散化間隔は、時間領域の離散化間隔に反比例し、時間領域のサンプリング(tlist)の数と、周波数領域サンプリング(flist)の数とは同数であるため、サンプリングした周波数のリストflistは以下で表せます。

flist = np.linspace(0, 1/dt, 1/dt/nt)

ここまでで、以下すべての実装が完了しました。

1. 端面の吸収境界を実装
2. アンテナ入力電流式を実装
3. アンテナ入力特性解析を実装

FDTD法は、原理が単純な解析手法であるため、機能拡張も簡単に実装できる利点があります。

解析実践

ここまでで、アンテナ入力特性の数値計算に必要な課題をすべてクリアしたので、実際に解析に入ります。

解析条件

数値解析の条件は、以下図に示した、$z$方向に$20$ cm、中心にデルタキャップ給電を与えるダイポールアンテナです。
ダイポールアンテナですので、解析的な解は$5$ GHzにおいて共振、すなわち最小の反射係数を示すことが期待されます。

使用したソースコードはこちら。

import cupy as cp
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

from tqdm import tqdm

c = 2.99792458e8 # 光速[m/s]
eps0 = 8.854187817e-12
mu0 = 1.2566370614e-6

dx = 0.001 # x方向空間差分間隔[m]

nx = 50 # x方向計算点数
ny = 50 # y方向計算点数
nz = 200 # z方向計算点数

dt = 0.99/(c * np.sqrt((1.0/dx ** 2 + 1.0/dx ** 2 + 1.0/dx ** 2))) # 時間差分間隔[s] c.f.Courantの安定条件
nt = 2 ** 16 # 計算ステップ数

# 電気定数初期化と更新係数の計算
eps = cp.full((nx, ny, nz), eps0)
mu = cp.full((nx, ny, nz), mu0)
sigma = cp.full((nx, ny, nz), 0.0)

# PML用のパラメータ
M = 2     # 吸収境界の導電率の上昇曲線の次数(2 - 3次が一般的)
R = 1e-6  # 境界面において実現したい反射係数
pmlN = 8  # PMLの層数、大きいほど計算コストが増えるが、反射率低減可

for ln in range(pmlN):
    sigma_value = ((pmlN - ln)/pmlN) ** M * ((M + 1) * (-np.log(R))/(2 * pmlN * dx * 120 * np.pi)) # PML吸収境界のsigma計算

    sigma[ln : ln + 1, :, :] = sigma_value
    sigma[:, ln : ln + 1, :] = sigma_value
    sigma[:, :, ln : ln + 1] = sigma_value

    sigma[-(ln + 1) : -ln, :, :] = sigma_value
    sigma[:, -(ln + 1) : -ln, :] = sigma_value
    sigma[:, :, -(ln + 1) : -ln] = sigma_value


dh = dt /(mu * dx) # 式(9) - (11)の右辺係数

ce = (2.0 * eps - sigma * dt)/(2.0 * eps + sigma * dt) # 式(12) - (14)の右辺第一項係数
de = 2.0 * dt /((2.0 * eps * dx) + (sigma * dt * dx)) # 式(12) - (14)の右辺第二項係数

# 電磁界初期化
t = 0.0

E_x = cp.zeros(shape=(nx, ny, nz))
E_y = cp.zeros(shape=(nx, ny, nz))
E_z = cp.zeros(shape=(nx, ny, nz))
H_x = cp.zeros(shape=(nx, ny, nz))
H_y = cp.zeros(shape=(nx, ny, nz))
H_z = cp.zeros(shape=(nx, ny, nz))

tlist = np.zeros(nt)
itime = np.zeros(nt)
vtime = np.zeros(nt)

for _ in tqdm(range(nt)):

    # 電界のz成分を励振
    Vin = -((t-100*dt)/dt) * cp.exp(-((t-100*dt)/dt)**2)
    E_z[nx//2, ny//2, nz//2] = -Vin/dx
    t += dt/2

    # 電界各成分計算
    E_x = ce * E_x + de * ((H_z - cp.roll(H_z, shift=1, axis=1))\
                          -(H_y - cp.roll(H_y, shift=1, axis=2)))

    E_y = ce * E_y + de * ((H_x - cp.roll(H_x, shift=1, axis=2))\
                         - (H_z - cp.roll(H_z, shift=1, axis=0)))

    E_z = ce * E_z + de * ((H_y - cp.roll(H_y, shift=1, axis=0))\
                         - (H_x - cp.roll(H_x, shift=1, axis=1)))

    E_z[nx//2, ny//2, nz//2 - 15: nz//2 + 15] = 0
    Eamp = cp.sqrt(E_x**2 + E_y**2 + E_z**2)

    # 電界のz成分を励振
    Vin = -((t-100*dt)/dt) * cp.exp(-((t-100*dt)/dt)**2)
    E_z[nx//2, ny//2, nz//2] = -Vin/dx
    t += dt/2

    # 磁界各成分計算
    H_x = H_x + dh * ((E_z - cp.roll(E_z, shift=-1, axis=1))\
                    - (E_y - cp.roll(E_y, shift=-1, axis=2)))

    H_y = H_y + dh * ((E_x - cp.roll(E_x, shift=-1, axis=2))\
                    - (E_z - cp.roll(E_z, shift=-1, axis=0)))

    H_z = H_z + dh * ((E_y - cp.roll(E_y, shift=-1, axis=0))\
                    - (E_x - cp.roll(E_x, shift=-1, axis=1)))


    Iin = dx * (H_x[nx//2, ny//2 - 1, nz//2] - H_x[nx//2, ny//2, nz//2])\
        + dx * (H_y[nx//2, ny//2, nz//2] - H_y[nx//2 - 1, ny//2, nz//2])


    if _ % 2 ** 8 == 0:
        plt.imshow(cp.asnumpy(Eamp)[:, :, nz//2], cmap="Reds")
        plt.colorbar()
        plt.savefig("output/" + str(_).zfill(8) + ".png")
        plt.close('all')

    tlist[_] = t
    itime[_] = Iin
    vtime[_] = Vin

細かい変更点としては、

• 給電点への電圧波形を微分ガウスパルスとした。
• 計算にGPUを用いた
• 反射係数等解析結果の可視化用スクリプトを足した
• 解析領域サイズ、離散化間隔をダイポールアンテナに合わせて変形した

特に、給電波形を変えた理由としては、以前のように正弦波を与えてしまうと、フーリエ変換した際に得られる周波数帯域が非常に狭く、妥当に得られるインピーダンスの幅が狭いためです。
ガウスパルスは、比較的広いスペクトルを持つため、応答波形も広いスペクトルを示し、一回の解析で広い帯域のインピーダンスを図ることができます。（ただし、高周波を含むためセルサイズとの兼ね合いで、ある程度の不確かさを見込む必要はありますが…。）

また、解析実行後、パルス応答波形が十分に収束していることが、安定したインピーダンス解析には必要な条件です。
給電点における電流や、周囲の電界などを見て、収束していることを確認しておきましょう。

解析結果

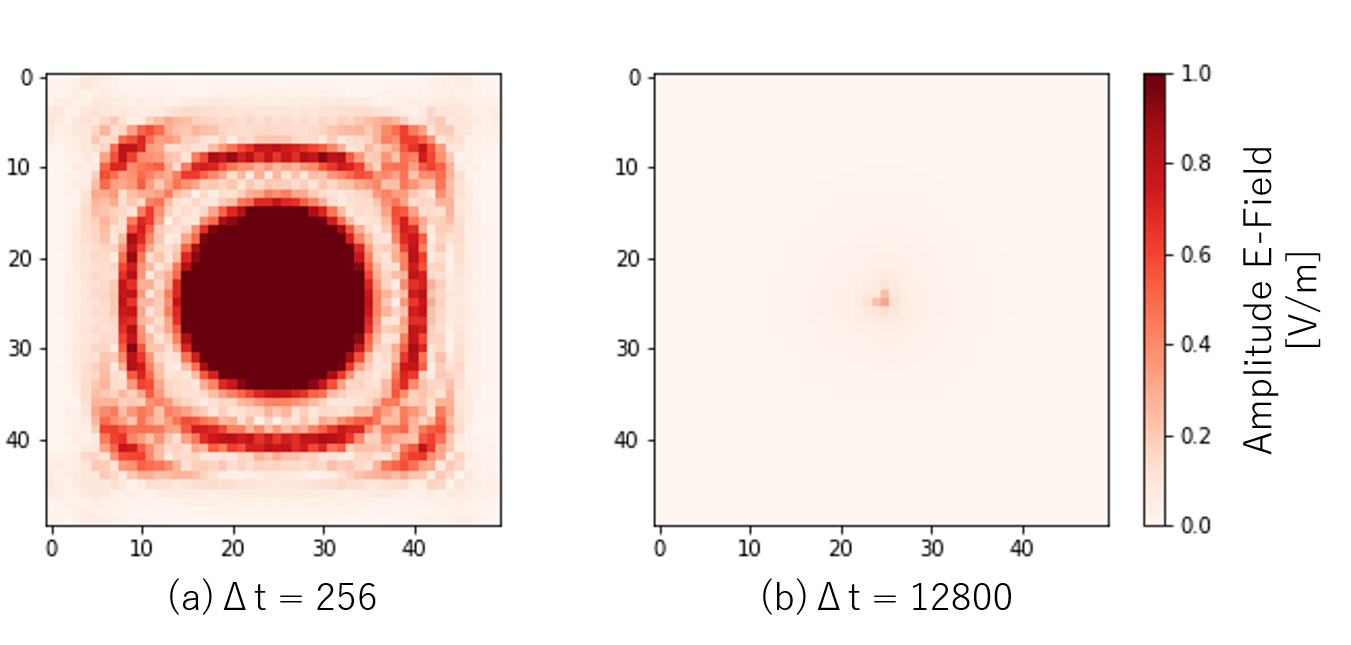
電界分布

まずはガウスパルスを与えた場合の電界強度分布です。十分時間が経過したのち、アンテナから放射された電界がすべて吸収境界によって消えているのがわかります。実際には$t = 65280 \Delta t$まで計算しているので、おそらく収束は十分そうですね。

反射係数

では実際に、入力インピーダンスを用いて、以下式$(7)$から反射係数$\Gamma$を求めた結果を確認しましょう（冒頭と同じ図）

\begin{aligned}
\Gamma = \frac{Z - Z_0}{Z + Z_0}　&...(7)\\
\end{aligned}

給電線としては、理想的な同軸ケーブルを用いたと想定して、$Z_0=50 \Omega$を用いています。

反射係数の周波数特性として、約4.00 GHzにおいて極小値、すなわち共振点が確認できました。
半波長ダイポールアンテナの共振波長は、およそアンテナ長の2倍であり、今回で言えば6 cmで周波数だと5.00 GHz付近が期待される共振点ですが、今回の解析結果は大きくずれてしまっていることがわかります。

考察

共振点が理論値とずれているのは、FDTD法ではセル境界が曖昧であるため、半セル分くらい想定より長いアンテナとなってしまっているため＋波長短縮効果によるものです。

また、記事を書いている途中で気づきましたが、今回の実装ではPML吸収境界に誤りがあり、実質機能していないため、端面からの反射の影響をもろに受けているためです。（多分これが支配的）

上記誤差の要因は、磁界の吸収境界が機能していなかった（実装できていなかった）ためでした。
修正した際の結果のみ以下に示しておきます。正した際の結果のみ以下に示しておきます。（2019/10/26修正）

4.66 GHz付近で共振しており、インピーダンスの放射成分も$73 \Omega$で、理論値に近い結果が得られていそうでした。

修正した箇所は、磁界の吸収境界追加と、磁界の更新係数です。

for ln in range(pmlN):
    sigma_value = ((pmlN - ln)/pmlN) ** M * ((M + 1) * (-np.log(R))/(2 * pmlN * dx * 120 * np.pi)) # PML吸収境界のsigma計算

    sigma[ln : ln + 1, :, :] = sigma_value
    sigma[:, ln : ln + 1, :] = sigma_value
    sigma[:, :, ln : ln + 1] = sigma_value

    sigma[-(ln + 1) : -ln, :, :] = sigma_value
    sigma[:, -(ln + 1) : -ln, :] = sigma_value
    sigma[:, :, -(ln + 1) : -ln] = sigma_value

#**************追記箇所***************
    sigmam[ln : ln + 1, :, :] = mu0/eps0 * sigma_value
    sigmam[:, ln : ln + 1, :] = mu0/eps0 * sigma_value
    sigmam[:, :, ln : ln + 1] = mu0/eps0 * sigma_value

    sigmam[-(ln + 1) : -ln, :, :] = mu0/eps0 * sigma_value
    sigmam[:, -(ln + 1) : -ln, :] = mu0/eps0 * sigma_value
    sigmam[:, :, -(ln + 1) : -ln] = mu0/eps0 * sigma_value


ch = (2.0 * mu - sigmam * dt)/(2.0 * mu + sigmam * dt) # 式(12) - (14)の右辺第一項係数
dh = 2.0 * dt /((2.0 * mu * dx) + (sigmam * dt * dx)) # 式(12) - (14)の右辺第二項係数
#**************追記箇所終わり***************

精度を上げるためにはサボってはいけない、という教訓を得たところで、次回からはもう少し本腰を入れた実装に取り組んでいきたいと思います。

ソースコード

以下のプロジェクト、impディレクトリ内にJupyter notebook形式ですべてのソースコードを記載しています。
https://github.com/sandship/practiceFDTD

まとめ

今回の結果としては、残念ながら低い精度の解析結果となってしまいましたが、時間領域の解法でありながら、周波数領域の解を得られるなど、FDTD法の有用性をお伝えできていればと思います。

また今後も、理論計算が実際の問題解決に役立つことを、数値計算の実例を以て紹介していきます。

次回は、吸収境界の話を更に深め、解析の精度を向上に取り組みたいと思います。