LoginSignup
11
14
@samuelladoco

SCIP ソルバー + Python + PySCIPOpt パッケージ で、手っ取り早く数理最適化モデルを構築して結構速く解く、ということが仕事でもタダでできそう

Last updated at Posted at 2023-06-05

※ 本記事執筆時点（2023/06/05）で、執筆者がネットから適当に拾った情報を元に手元環境で試したものです

概要

  • 数理最適化ソルバー SCIP が Apache 2.0 License （日本語参考訳） になっているので、 仕事でもタダで SCIPを使って数理最適化モデルを解くことができそう
  • Python + PySCIPOpt パッケージ を使えば、手っ取り早く数理最適化モデルが構築でき、 SCIPで結構速く 解けそう
    • Python + PuLP や Python + Python-MIP でも手っ取り早く数理最適化モデルは構築できるが、これらに同こんされているデフォルトの数理最適化ソルバー（COIN-CBC）はSCIPより遅い
      • ただし、 PuLP や Python-MIP はほかの数理最適化ソルバーをインストールしていればそちらを使うよう設定変更ができる
        • しかし、 PuLP でほかの数理最適化ソルバーを使用する際は、PuLP とはファイルベースのやりとりが発生するソルバーがあり、そういうソルバーを使用する場合はファイルの生成・入出力に時間がかかる場合がある
        • Python-MIP からは SCIP を使用できない

試した環境

  • Windows 11 22H2 (22621.1778)
    • Windows 11 は64ビットOSです（32ビット版は存在しません）
    • Windows 10 64ビット版 や macOS 、最近の各種 Linux でも動くはずです
      • macOS 、 Linux は、導入手順が結構違うみたいです
    • 32ビットOSでもできるようですが、使用できるメモリー量の関係から32ビットOS上で数理最適化をすることはお勧めできません
  • 公式の Python 3.11.2 （64ビット版Windows用）
  • SCIP 8.0.3 for Windows 64bit
    • Apache 2.0 License が適用されるのは 8.0.3 とそれ以降のバージョン です
  • PySCIPOpt 4.3.0
    • SCIP と PySCIPOpt はお互いに対応するバージョンの組が決まっており、合わせる必要があるようです

導入手順

  1. SCIP公式サイト の Download → SCIPOptSuite-8.0.3-win64-VS15.exe をダウンロード
  2. その下の Visual C++ Redistributable Packages をクリック → Microsoftのページに飛ぶので In this article の下の Visual Studio 2015, 2017, 2019, and 2022 をクリック → https://aka.ms/vs/17/release/vc_redist.x64.exe をダウンロード
  3. 2.のほうを先に インストール
  4. 1.をインストール
    • 最初に SCIPOptSuite を 環境変数 PATH に加えるか否か選択させられるが、少なくとも Python + PySCIPOpt を使う場合はデフォルトの選択肢（加えない）を選んでも問題ない
      • もし必要になったら、そのときに自分で作業すればよい
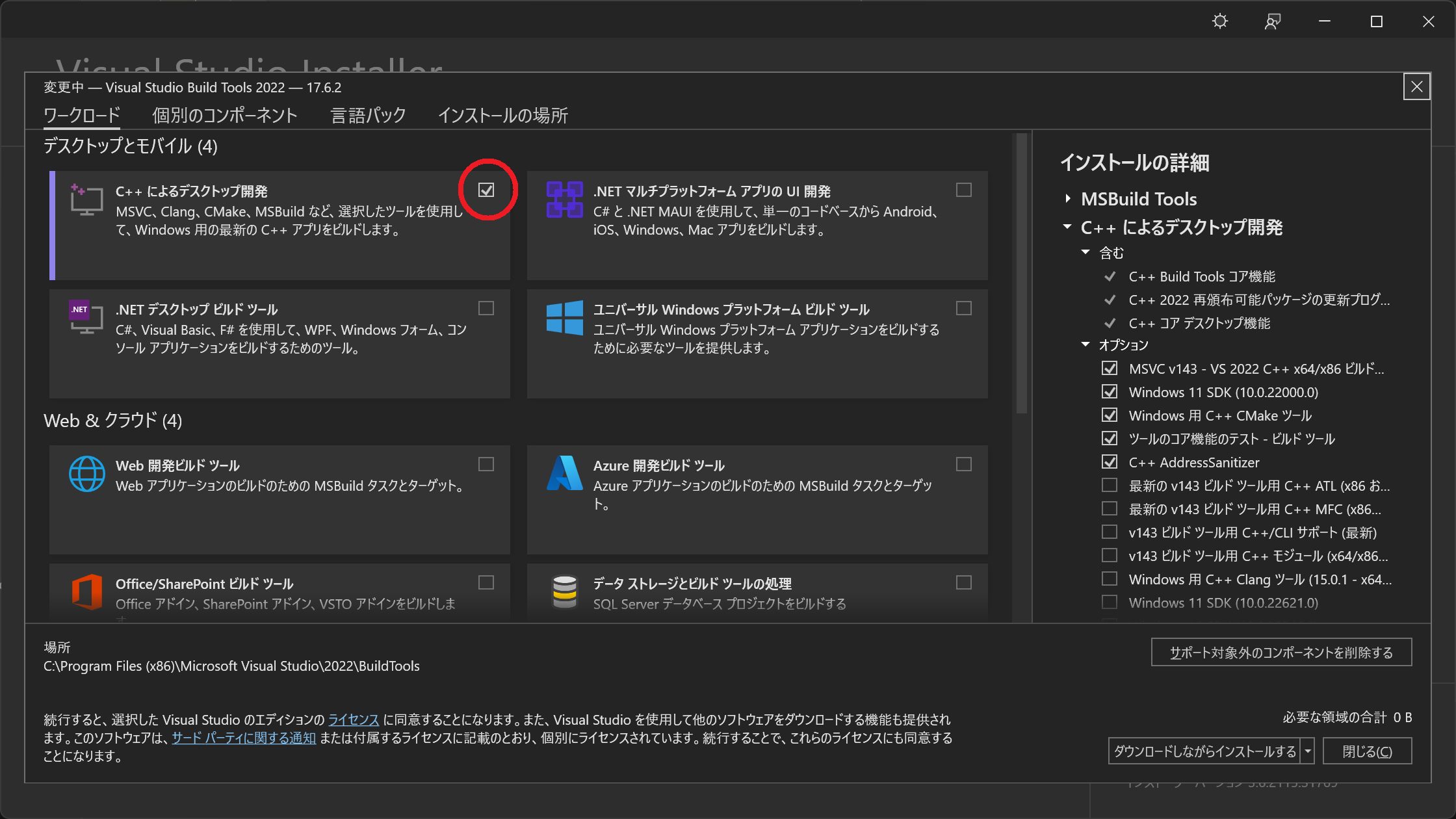
  5. Microsoft C++ Build Tools公式サイト の Build Tools のダウンロード をクリックして vs_BuildTools.exe をダウンロード
  6. 5.をインストール
    • このとき、下図の赤丸で囲まれたところをチェック
      • 不要な機能もインストールされそうなので、もし何が不要なのかがわかっていれば、右の インストールの詳細 から不要な機能のチェックを外してもよい
    • 5.と6.は、Visual Studio （たぶん2015以降）のC++ビルドツール（64bit対応版）がすでにインストールされていれば、スキップできる可能性が高い
      vsa.png
  7. 環境変数 SCIPOPTDIR を作成し、値にSCIPのインストールフォルダーを設定
    • 値の例： C:\Program Files\SCIPOptSuite 8.0.3
      • ユーザー環境変数に設定するかシステム環境変数に設定するかは、お好みで
    • 環境変数 PATH に %SCIPOPTDIR%\bin （または (SCIPのインストールフォルダー)\bin ）を追加する必要もあるかもしれないが、試した環境では不要だった
  8. コンソールで python -m pip install pyscipopt と打ち、 PySCIPOpt をインストール
    • コンソールの例： コマンド プロンプト 、 Windows PowerShell 、 Git Bash
    • python.exe のあるフォルダーが 環境変数 PATH に含まれていない場合（パスが通っていない場合）は、 (python.exeのあるフォルダーへの絶対パスまたは相対パス)\python -m pip install pyscipopt と打つ
    • なるべく Python仮想環境 を作ってその中でやりましょう

最適化モデルの例

昔書いた PuLP を使ったコード を PySCIPOpt 用に書き換えます。ついでにきれいにします。

problem2_pyscipopt.py
# Import
# -----------------------------------------------------------------------------
import time
from typing import Any

import pyscipopt


# Main
# -----------------------------------------------------------------------------
print(f"-" * 8)


# 作業員の集合（便宜上、リストを用いる）
I: list[str] = ["Aさん", "Bさん", "Cさん"]

print(f"作業員の集合 I = {I}")


# タスクの集合（便宜上、リストを用いる）
J: list[str] = ["仕事イ", "仕事ロ", "仕事ハ"]

print(f"タスクの集合 J = {J}")


# 作業員 i を タスク j に割り当てたときのコストの集合（一時的なリスト）
cc: list[list[int]] = [
    [1, 2, 3],
    [4, 6, 8],
    [10, 13, 16],
]

# cc はリストであり、添え字が数値なので、
# 辞書 c を定義し、例えば cc[0][0] は c["Aさん", "仕事イ"] でアクセスするようにする
c: dict[tuple[str, str], int] = {}  # 空の辞書
for i in I:
    for j in J:
        c[i, j] = cc[I.index(i)][J.index(j)]

print(f"コスト c[i,j]: ")
for i in I:
    print(f"    ", end="")
    for j in J:
        print(f"c[{i},{j}] = {c[i,j]:2d},  ", end="")
    print(f"")
print(f"")


# 数理最適化モデルを宣言
m: pyscipopt.Model = pyscipopt.Model(
    problemName="Problem-2",
)


# 変数集合を表す辞書
x: dict[tuple[str, str], Any] = {}  # 空の辞書
# x[i,j] または x[(i,j)] で、(i,j) というタプルをキーにしてバリューを読み書き

# 0-1変数を宣言
for i in I:
    for j in J:
        x[i, j] = m.addVar(
            name=f"Var_x({i},{j})",
            vtype="B",
        )


# 目的関数を宣言
m.setObjective(
    pyscipopt.quicksum(c[i, j] * x[i, j] for i in I for j in J),
    sense="minimize",
)


# 制約条件を宣言
# 各作業員 i について、割り当ててよいタスク数は1つ以下
for i in I:
    m.addCons(
        pyscipopt.quicksum(x[i, j] for j in J) <= 1,
        name=f"Constraint_leq_{i}",
    )

# 各タスク j について、割り当てられる作業員数はちょうど1人
for j in J:
    m.addCons(
        pyscipopt.quicksum(x[i, j] for i in I) == 1,
        name=f"Constraint_eq_{j}",
    )


print(f"-" * 8)


# 計算
time_start: float = time.perf_counter()
m.optimize()
time_stop: float = time.perf_counter()
print(f"")


print(f"-" * 8)


# （解が得られていれば）目的関数値や解を表示
print(f"最適性 = {m.getStatus()}, ", end="")
print(f"目的関数値 = {m.getObjVal()}, ", end="")
print(f"計算時間 = {time_stop - time_start:.3f} (秒)")
print(f"解 x[i,j]: ")
for i in I:
    print(f"    ", end="")
    for j in J:
        print(f"{x[i,j]} = {m.getVal(x[i,j])},  ", end="")
    print(f"")
print(f"")

上記例を実行して（解いて）得られた出力

--------
作業員の集合 I = ['Aさん', 'Bさん', 'Cさん']
タスクの集合 J = ['仕事イ', '仕事ロ', '仕事ハ']
コスト c[i,j]:
    c[Aさん,仕事イ] =  1,  c[Aさん,仕事ロ] =  2,  c[Aさん,仕事ハ] =  3,
    c[Bさん,仕事イ] =  4,  c[Bさん,仕事ロ] =  6,  c[Bさん,仕事ハ] =  8,
    c[Cさん,仕事イ] = 10,  c[Cさん,仕事ロ] = 13,  c[Cさん,仕事ハ] = 16,

--------
presolving:
   (0.0s) running MILP presolver
   (0.0s) MILP presolver found nothing
(round 1, exhaustive) 0 del vars, 0 del conss, 0 add conss, 0 chg bounds, 0 chg sides, 0 chg coeffs, 6 upgd conss, 0 impls, 6 clqs
   (0.0s) probing cycle finished: starting next cycle
   (0.0s) symmetry computation started: requiring (bin +, int -, cont +), (fixed: bin -, int +, cont -)
   (0.0s) no symmetry present
presolving (2 rounds: 2 fast, 2 medium, 2 exhaustive):
 0 deleted vars, 0 deleted constraints, 0 added constraints, 0 tightened bounds, 0 added holes, 0 changed sides, 0 changed coefficients
 0 implications, 6 cliques
presolved problem has 9 variables (9 bin, 0 int, 0 impl, 0 cont) and 6 constraints
      6 constraints of type <setppc>
transformed objective value is always integral (scale: 1)
Presolving Time: 0.00

 time | node  | left  |LP iter|LP it/n|mem/heur|mdpt |vars |cons |rows |cuts |sepa|confs|strbr|  dualbound   | primalbound  |  gap   | compl.
p 0.0s|     1 |     0 |     0 |     - |  clique|   0 |   9 |   6 |   6 |   0 |  0 |   0 |   0 | 0.000000e+00 | 2.300000e+01 |    Inf | unknown
p 0.0s|     1 |     0 |     0 |     - |   locks|   0 |   9 |   6 |   6 |   0 |  0 |   0 |   0 | 0.000000e+00 | 1.900000e+01 |    Inf | unknown
  0.0s|     1 |     0 |     6 |     - |   655k |   0 |   9 |   6 |   6 |   0 |  0 |   1 |   0 | 1.900000e+01 | 1.900000e+01 |   0.00%| unknown

SCIP Status        : problem is solved [optimal solution found]
Solving Time (sec) : 0.00
Solving Nodes      : 1
Primal Bound       : +1.90000000000000e+01 (2 solutions)
Dual Bound         : +1.90000000000000e+01
Gap                : 0.00 %

--------
最適性 = optimal, 目的関数値 = 19.0, 計算時間 = 0.005 (秒)
解 x[i,j]:
    Var_x(Aさん,仕事イ) = 0.0,  Var_x(Aさん,仕事ロ) = 0.0,  Var_x(Aさん,仕事ハ) = 1.0,
    Var_x(Bさん,仕事イ) = 0.0,  Var_x(Bさん,仕事ロ) = 1.0,  Var_x(Bさん,仕事ハ) = 0.0,
    Var_x(Cさん,仕事イ) = 1.0,  Var_x(Cさん,仕事ロ) = 0.0,  Var_x(Cさん,仕事ハ) = 0.0,

パラメーター設定

例えばこんな感じでします。

m.setParam("limits/time", 300.0)  # 計算時間の上限を設定

設定できるパラメーターの一覧とデフォルト値は、

m.writeParams(
    "./params_default.txt",
    onlychanged=False,
)

と書いて実行すると params_default.txt というファイルが生成されるので、その中身を見ればわかります。

これ以上の細かいこと

11
14
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
11
14