はじめに
日頃から回帰分析を行う際に、変数選択を行なった際のモデルによる結果は正しいのかということが、常に疑問に感じていました。
その時に、変数選択がその後の統計的推定に与える影響を加味した推定を行うためのselective inferenceを知りました。
そして、統計関連学会連合大会にて「selective inferenceの基礎と応用」というチュートリアルがあり受講してきました。
今回はその内容を中心にselective inferenceの基本をまとめたいと思います。(個人的なまとめに過ぎないので悪しからず)
統計分析結果を公開する時のバイアス
近年では知識駆動型とデータ駆動型の仮説形成が対比されることがあります。
それぞれの形式は次のように表現できます。

知識駆動型科学における仮説検定では、データとは独立に研究対象における経験と知識により仮説形成をおこなっています。
そして、データを用いて仮説の検証を行なっていく流れをとります。
具体的には、研究対象やドメインに関する知見から説明変数間の関係・構造を仮定し、回帰モデル等を作成していくことで分析を行います。
一方で、データ駆動型科学では、得られているデータを元に仮説形成をおこなっています。
具体的には、stepwiseやスパース推定により線形回帰のモデルを選択することや、クラスタリングアルゴリズのよりクラスを形成してクラス間の差の検定を行う場合があげられます。
知識駆動型科学との大きな違いは、同一のデータを二回使って仮説の形成と検定を行なっているところになります。
近年では、多様なデータが豊富に収集されることが一般になってきたことから、データ駆動型科学における仮説検定を行う場合が増えてきていると感じています。
データ駆動型科学における仮説検定の結果には、仮説選択バイアスと呼ばれるバイアスが生まれてしまいます。
仮説選択バイアスの例として次のようなものが挙げられます。
ある遺伝子に対する薬剤の効果を調べるために、効果あり群となし群で有意水準を$\alpha=0.05$として有意な差があるかの仮説検定を行いました。
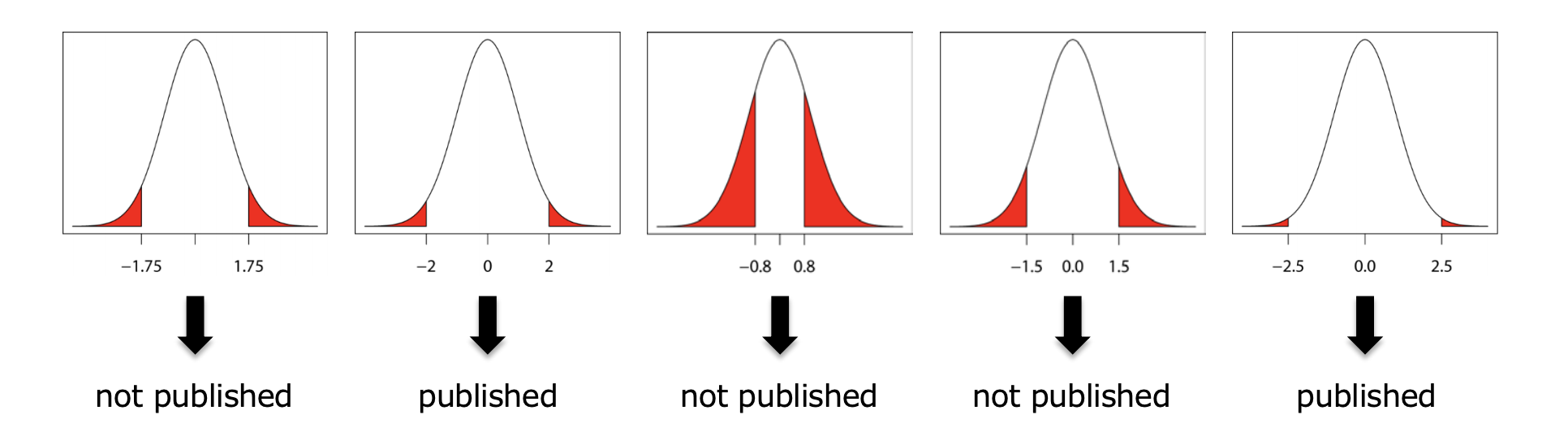
この時、p値が有意水準を満たした結果のみ公開されることが多いです。
また、検定を行う前に効果量が小さいと考えられる場合には、検定を行わない、ある程度の効果量がある場合のみ検定を行うというプロセスが取られる場合もあります。
読者としては発表された結果した見ることができません。
そのため、このような場合に結果に生じる仮説選択バイアスは、出版バイアスと呼ばれています。
(出典)
出版バイアスの詳しい内容はWikiを参考に。
このようなバイアス乗ってしまっている結果の中で、どのように結果を信頼していくべきかという問題が出てきます。
この時に重要になってくるのが、仮説選択によって発生するバイアスを除いた推定であるSelective Inferenceです。
Selective Inferenceの話を進めていくために、はじめに線形回帰分析における仮説選択バイアスを確認していきます。
線形回帰分析におけるバイアス
線形回帰モデルの場合では、特徴選択アルゴリズムを$A_{FS}$と表現する時、選択された特徴(説明変数)の集合を次にように表現できます。
\hat M ← A_{FS}(X,y)
選択された特徴のみで作成した線形モデルは次にように表現します。
y=X_{\hat M}\beta_{\hat M}+\epsilon , \epsilon \sim N(0, \sigma^2I)
そして、このモデルにより推定された係数$\beta_{\hat M,j}$が0であるかの統計的仮説検定を検討していきます。
しかし、$\beta_{\hat M,j}$の標本分布は特徴選択アルゴリズム$A_{FS}$に依存してしまいます。
そのため、そのままでは検定してはいけません。
ここで本当にバイアスが乗るのかを、確認してみたいと思います。
こちらに示す結果を得るためのRコードはGithubにあげており、記事上では省略します。
では、次にような回帰モデルを検討します。
y = 0.3X_1+0.2X_2+0.4X_3+0.65X_4+0.8X_5+\epsilon, \epsilon \sim N(0.5,1)
このモデルの説明変数に加えモデルおける係数が0となる変数を5つを考え、計10変数のデータがそれぞれ標準正規分布からサンプリングして得られているとします。
今回は一回のサンプルサイズ50としました。各サンプルではstepwiseによる変数選択を行います。
選択された変数の係数関して有意水準$\alpha=0.05$とした検定を行います。
これを2000回繰り返し、棄却割合を求めました。
通常の回帰分析における棄却割合は、有意水準$\alpha=0.05$と等しくなるはずです。
棄却割合=棄却された数/検定を行なった回数
実際の変数選択を行わなかった場合の棄却状態は次にようになりました。
モデルに含まれない変数の係数において、概ね5%程度の帰無仮説の棄却が行われています。
| $\beta_1$ | $\beta_2$ | $\beta_3$ | $\beta_4$ | $\beta_5$ | $\beta_6$ | $\beta_7$ | $\beta_8$ | $\beta_9$ | $\beta_{10}$ | |
|---|---|---|---|---|---|---|---|---|---|---|
| 棄却された数 | 1900 | 1363 | 1990 | 2000 | 2000 | 93 | 89 | 96 | 104 | 88 |
| 棄却されたかった数 | 100 | 637 | 10 | 0 | 0 | 1907 | 1911 | 1904 | 1896 | 1912 |
帰無仮説のもとでのp値は一様分布に従うことが知られているため、確認をしてみます。
$\beta_7$に関するp値の分布を確認すると、次にように一様分布になっていました。
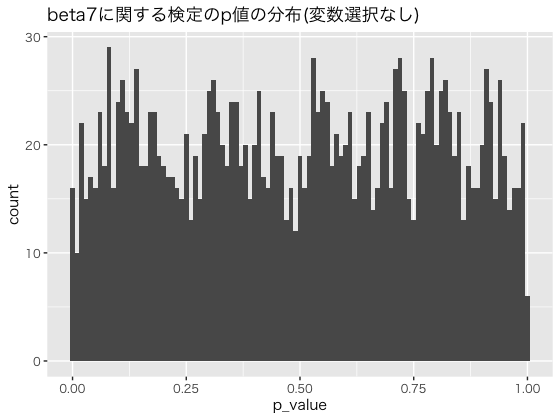
次に、stepwiseによる変数選択を行った場合の帰無仮説の棄却状態を確認してみました。
| $\beta_1$ | $\beta_2$ | $\beta_3$ | $\beta_4$ | $\beta_5$ | $\beta_6$ | $\beta_7$ | $\beta_8$ | $\beta_9$ | $\beta_{10}$ | |
|---|---|---|---|---|---|---|---|---|---|---|
| 棄却された数 | 1937 | 1451 | 1994 | 2000 | 2000 | 105 | 124 | 118 | 125 | 117 |
| 棄却されたかった数 | 45 | 351 | 1 | 0 | 0 | 318 | 312 | 298 | 269 | 288 |
| 選択されたかった回数 | 18 | 198 | 1 | 0 | 0 | 1577 | 1564 | 1584 | 1606 | 1595 |
棄却割合が0.05より大きくなっておりバイアスが存在していると考えられます。
得られているデータによっては、回帰係数が0の説明変数を有意な値であると判断してしまう可能性が非常に高くなってしまいます。
こちらも、$\beta_7$に関するp値の分布を確認してみます。
0.0付近に多くのサンプルが存在し一様分布に従っていないです。
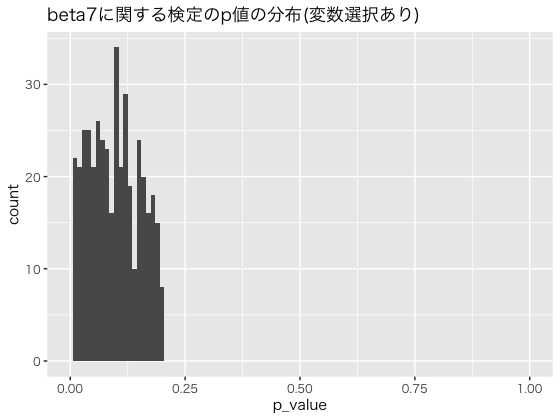
これらのことから、変数選択を行わない場合に比べて大きなバイアスが存在してしまっていることがわかります。
古典的な対策方法
このような場合にバイアスのない推定を行うための古典的な手法としてData Splittingがあります。
次にような方法です。
- データをランダムに分割する$Y=(Y_1,Y_2)$
- $Y_1$をモデル(仮説)選択を行う
- $Y_2$を選択した仮説の推定に用いる
上記のシミュレーションと同じ設定で、Data Splittingを適用してみたいと思います。
結果を確認すると次のようになりました。
| $\beta_1$ | $\beta_2$ | $\beta_3$ | $\beta_4$ | $\beta_5$ | $\beta_6$ | $\beta_7$ | $\beta_8$ | $\beta_9$ | $\beta_{10}$ | |
|---|---|---|---|---|---|---|---|---|---|---|
| 棄却された数 | 1120 | 495 | 1604 | 1979 | 1997 | 30 | 31 | 33 | 29 | 37 |
| 棄却されたかった数 | 665 | 890 | 305 | 19 | 1 | 597 | 591 | 564 | 600 | 564 |
| 選択されたかった回数 | 18 | 198 | 1 | 0 | 0 | 1373 | 1378 | 1403 | 1371 | 1399 |
概ね、5%程度の棄却率となっており、バイアスのない推定ができていると考えられます。
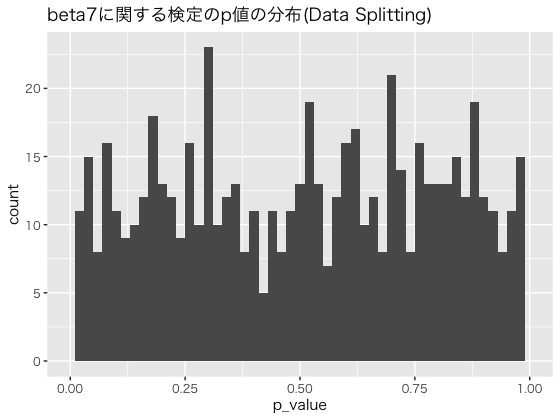
$\beta_7$に関するp値の分布を確認すると次にようになっており、一様分布に近いものになっていると考えられます。
しかし、この方法ではデータが独立な場合(i.i.d)が求められますし、選択にも推定にも使えるデータ量が減ってしまいます。
また、ここでは解説しませんが、推定に利用できる情報量が減ってしまいます。
selective inference
こちらの資料では次のように説明していました。
「Selective Inferenceとは、データに基づいて選択された仮説を同一のデータで評価する際に、選択バイアスを除去するため、仮説を選択するイベントの条件付分布により統計的仮説検定を行うものである。」
selective inferenceの考え方
ここで、アルゴリズム等によってどのように仮説が選択されているのかを考えます。
仮説選択アルゴリズムを次のように表現できます。
\boldsymbol{A}: \{ \delta_A,\delta_B,\dots,\delta_Z \} \rightarrow \hat M \subseteq \{A,B,\dots,Z \}
この時の仮説とは、回帰分析では説明変数のセットやクラスタリングにおけるクラス状態等があげられます。
アルゴリズムによってどのようなデータが選択されたことにより、仮説が選択されたのかを定義します。
これは仮説選択アルゴリズムの逆像と呼ばれるもので、アルゴリズムにより選択されたデータ空間であり、次のように表現します。
D:=\{\delta | \hat M ← \boldsymbol{A}(\delta)\}
イメージとしては次のような形です。
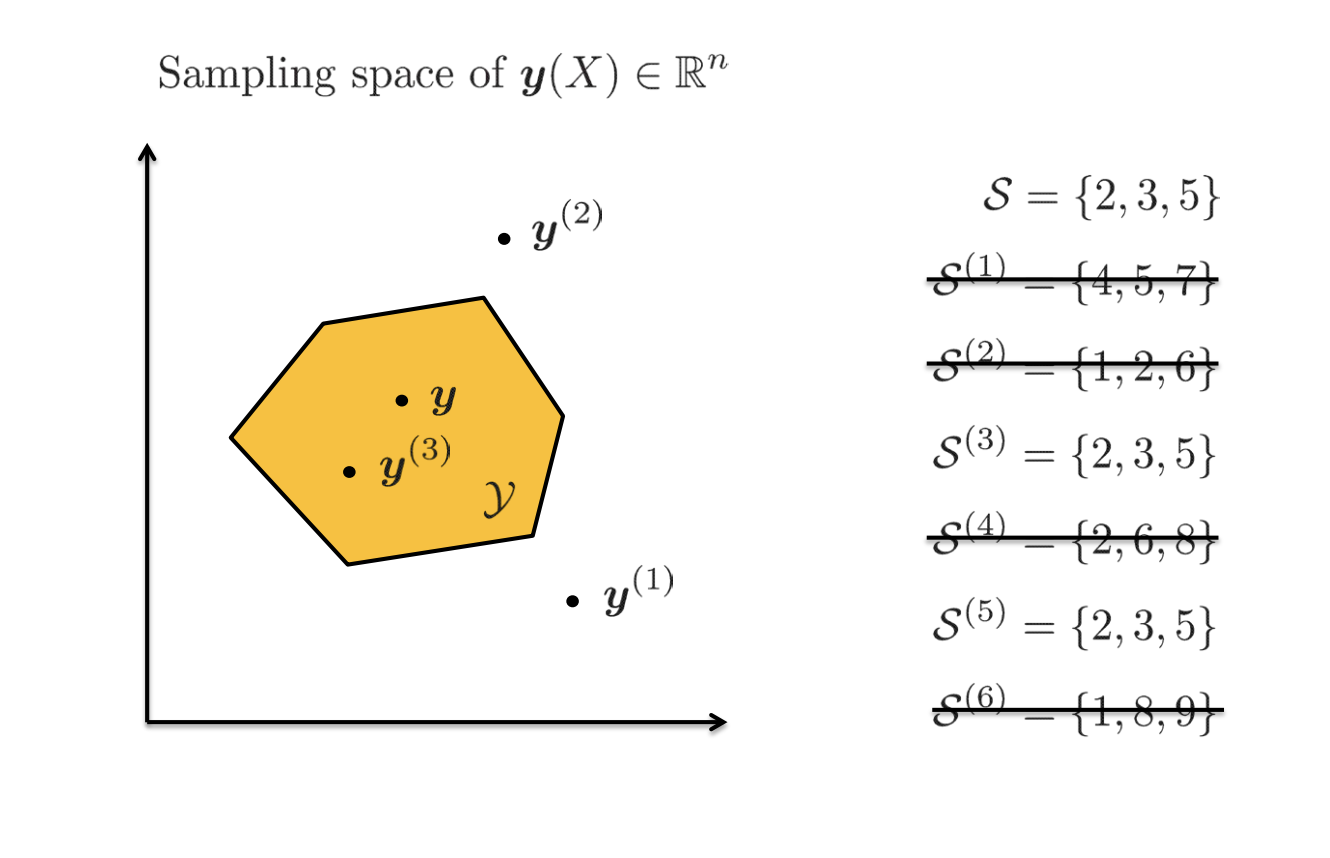
(出典)
この逆像に対応するデータの領域が選択された場合に推定を行います。
逆像Dによって条件付けられた推論(条件付推論:Conditional inference)を行えば、仮説選択バイアスを修正することができます。
P(|\delta_k|>\theta|k \in \boldsymbol{A}(\delta))=P(|\delta_k|>\theta|\delta \in D)=\alpha
回帰分析の時の場合は、偏回帰係数の統計的有意性を検定する際に、仮説選択(変数選択)イベントに関する逆像を与えることで、バイアスを除くselective inferenceを行うことができます。
selective inferenceで用いる信頼区間やp値は、selective CIsとselective p-valueと呼ばれます。
これらの推定に用いられる分布には切断正規分布を用い、selective p-valueを次のように算出します。
p^{SI}_{\hat M,j}=1-F^{E(y)}_{0,1}
\left(
\frac{\left|\hat \beta_{\hat M ,j}\right|}
{\sigma^2 (X_{\hat M}^T X_{\hat M})^{-1}_{jj}}
\right)
ここで、$F^{E}_{0,1}$は平均$0$、分散$1$、分断領域$E$の切断正規分布の累積分布関数です。
ちなみに、通常の推定におけるp-valueは次のように表現できます。
P^{OR}_j=1-\Phi \left(\frac{\left|\hat \beta_j\right|}{\sigma {(X^TX^{-1}_{jj})}}\right)
線形不等式による選択イベント
selective inferencedeha特徴選択イベントの逆像をうまく算出することが重要になってきます。
Lee at al.(2016)は次式のように特徴選択イベント$M$を表現できる場合、Selective Inferenceが可能になることを提案しました。
これは、逆像の空間を線形な境界線により選択することを意味します。
Ay \leq b
\tag{1}
イメージとしては次のような感じです。
 [(出典)](https://www.ieice.org/~sita/forum/article/2019/201903231310.pdf)
[(出典)](https://www.ieice.org/~sita/forum/article/2019/201903231310.pdf)
実際の選択アルゴリズムは、次のようなものが挙げられます。
それぞれにおいて上記の特徴選択イベントを線形な境界線で表現できます。
- Marginal screeningのような定義に基づいたもの
- LASSOのような最適性条件に基づいたもの
- Stepwiseのようなアルゴリズムに基づいたもの
一つ目と二つ目に選択アルゴリズムにおいて、線形な形で表現できることを確認します。
Marginal screeningのような定義に基づいたもの
Marginal screeningとは目的変数と相関が大きい上位$k$個の特徴量を選択する方法です。($k$は事前に決定されている)
特徴量$x_j$と目的変数$y$が平均0と分散1に標準化されている場合、相関は内積$x^T_jy$となります。
特徴量のインデックスを相関係数の絶対値の降順に並び替えると次のようになります。
|x^T_{(1)}y| \geq |x^T_{(2)}y|\geq |x^T_{(3)}y|\geq \dots \geq |x^T_{(d)}y|
再左辺からk個に対応する特徴量を選択することが、Marginal screeningに対応し,次のようなアルゴリズムとして解釈できます。
\{\hat M, \hat s\} ← \boldsymbol{A}_{MS}(X,y)
ここで,$\hat M ={(1),(2),\dots,(k)}$,$s=[sign(x^T_{(1)}y),sign(x^T_{(2)}y),\dots,sign(x^T_{(k)}y)]$です。
MSの定義により選択された特徴1~k番目までと選択されない特徴k+1~d番目は以下の関係となる。
|x^T_{(1)}y| \geq \dots \geq |x^T_{(k)}y| \geq |x^T_{(k+1)}y| \geq \dots \geq |x^T_{(d)}y|
この関係を書き下すと次のようになります。
\begin{matrix}
\hat s_{(1)}x_{(1)}^Ty \leq \pm x_{(k+1)}^Ty,&\hat s_{(1)}x_{(1)}^Ty \leq \pm x_{(k+2)}^Ty,&\dots,& \hat s_{(1)}x_{(1)}^Ty \leq \pm x_{(d)}^Ty \\
\hat s_{(1)}x_{(1)}^Ty \leq \pm x_{(k+1)}^Ty,&\hat s_{(1)}x_{(1)}^Ty \leq \pm x_{(k+2)}^Ty,&\dots,& \hat s_{(2)}x_{(2)}^Ty \leq \pm x_{(d)}^Ty \\
\vdots&\vdots&\ddots&\vdots\\
\hat s_{(k)}x_{(k)}^Ty \leq \pm x_{(k+1)}^Ty,&\hat s_{(k)}x_{(k)}^Ty \leq \pm x_{(k+2)}^Ty,&\dots,& \hat s_{(k)}x_{(k)}^Ty \leq \pm x_{(d)}^Ty \\
\end{matrix}
全ての不等式をまとめると選択イベントはデータ空間の線形分離として表現できます。
Ay \leq 0
LASSOのような最適性条件に基づいたもの
LASSOは次のような最適化問題を考えるモデルです。
\hat \beta =argmin_{beta}J(\beta)=\frac{1}{2}||y-X\beta||^2_2+\lambda ||\beta||_1
$\hat \beta$が最適解であるための必要十分条件は次のように表すことができる。
\partial J(\beta)=X^T(X \beta - y)+\lambda \partial \parallel \beta \parallel_1 =0
ここで、$\partial f(z)$は関数$f(z)$の劣微分を表すものであり、$\partial \parallel \beta \parallel_1$はこの時-1か1をとる。
最適性条件を選択された特徴と選択されなかった特徴に関する部分に分割すると以下のように表現される。
X^T_{\hat M}(X_{\hat M} \beta_{\hat M} - y)+\lambda \hat s =0 \\
X^T_{\hat M}(X_{\hat M} \beta_{\hat M} - y) \in \lambda [-1,1]
アルゴリズムの出力${\hat M,\hat s}$が与えられた時、選択イベントは以下のように定義されます。
\boldsymbol{A}
:=
\left\{{
\:
y \in \mathbb{R}^n
\:
\left|
\exists \gamma \in R^{| \hat M|}
\: s.t. \:
\begin{array}{ll}
X^T_{\hat M}(X_{\hat M} \gamma - y) + \lambda \hat s =0 \\
X^T_{\hat M}(X_{\hat M} \gamma - y) \in \lambda [-1,1] \\
sign(\gamma)=\hat s
\end{array}
\right.}
\right.
\tag{2}
式(2)の一つ目の条件から$\gamma$が求まる。
\gamma = (X^T_{\hat M}X_{\hat M})^{-1}(X^T_{\hat M}y-\lambda \hat s)
\tag{3}
これを初めの式(2)の二つ目の条件に代入すると次のようになります。
\frac{1}{\lambda}(X^T_{\hat M}X_{\hat M})(X^T_{\hat M}X_{\hat M})^TX^T_{\hat M}y
\leq1+X^T_{\hat M}X_{\hat M}(X^T_{\hat M}X_{\hat M})^{-1} \hat s
\Leftrightarrow A_1y \leq b_1
\\
-\frac{1}{\lambda}(X^T_{\hat M}X_{\hat M})(X^T_{\hat M}X_{\hat M})^TX^T_{\hat M}y
\leq1+X^T_{\hat M}X_{\hat M}(X^T_{\hat M}X_{\hat M})^{-1} \hat s
\Leftrightarrow A_2y \leq b_2 \\
式(3)を式(2)の三つ目の条件に代入すると次のようになります。
\begin{aligned}
sign(\gamma)=\hat s \Leftrightarrow \; &
diag(\hat s) \gamma >0 \\
\Leftrightarrow \; &
diag(\hat s)(X^T_{\hat M}X_{\hat M})^{-1}X_My<\lambda (X^T_{\hat M}X_{\hat M})^{-1} \hat s \\ \Leftrightarrow \; & A_3y \leq b_3
\end{aligned}
以上の関係をまとめると次のようになり、LASSOによる選択イベントは線形な形で表現できます。
\boldsymbol{A}
:=
\left\{
{
\:
y \in \mathbb{R}^n
\:\left|\:
{
\left[
\begin{array}{ll}
A_1\\
A_2\\
A_3
\end{array}
\right]
y<
\left[
\begin{array}{ll}
A_1\\
A_2\\
A_3
\end{array}
\right]
}
\right.
}\:
\right\}
特徴選択後の線形モデル
応答変数$y$に正規性を仮定します。
y \sim N(\mu, \sigma^2 I)
ただし、$\mu \in \mathbb{R}^n $は未知で、$\sigma^2$は既知とします。
ここで、以下のような統計的仮説検定を考えます。
H_0^{\hat M,j} : \beta_{\hat M,j}=0 \\
H_1^{\hat M,j} : \beta_{\hat M,j} \neq 0
検定統計量$\hat \beta_{\hat M,j}$は以下のように$y$との内積の形を書くことができます。
\hat \beta_{\hat M,j} = e_j^T(X_{\hat M}^TX_{\hat M})^{-1}X_{\hat M}^Ty=\eta^Ty
$y$を$\eta$と選択後の直交補空間へ分解します。
y=\eta(\eta^T\eta)^{-1}\eta^Ty+(I+\eta(\eta^T\eta)^{-1}\eta^T)y=c(\eta^Ty)+z
ここで、式(1)による条件付けは次にように変換できます。
Ay \leq b \Leftrightarrow \{ A(c(\eta^Ty)+z)\}\leq b \Leftrightarrow A(\eta^Ty) \leq b -Az
ここで要素ごとの不等式に分けることができます。
Ay \leq b \Leftrightarrow
\left\{
\begin{array}{ll}
\eta^Ty \leq \frac{(b-\eta^Ty)_h}{(Ac)_h} & for\, h:(Ac_h)>0 \\
\eta^Ty \geq \frac{(b-\eta^Ty)_h}{(Ac)_h} & for\, h:(Ac_h)<0 \\
(b-\eta^Ty)_h \geq 0 & for\, h:(Ac_h)=0
\end{array}
\right.
ある$z=z_0$に固定すると、$\hat \beta_{\hat M ,j}=\eta^Ty$のとうる範囲が以下のようになります。
min_{h:(Ac_h)<0} \frac{(b-\eta^Ty)_h}{(Ac)_h} \leq \eta^Ty \leq min_{h:(Ac_h)<0} \frac{(b-\eta^Ty)_h}{(Ac)_h}
そのため、帰無仮説$H_0^{\hat M ,j}$のもとで$\hat \beta_{\hat M ,j}=\eta^Ty$は、式1の条件のもとで以下の切断正規分布に従います。
\{\eta ^Ty|(\hat M, \hat s)=(M,s),z=z_0\}
\sim
TN(0,\sigma^2(X_M^TX_M)^(-1)_{jj},[V^-(z),V^+(z)])
切断正規分布$TN(\mu,\sigma^2,E)$の累積密度関数を$F_{\mu,\sigma^2}^{E}$と表現しすると、今回の切断正規分布は次のように表現することができます。
この切断正規分布の累積分布関数$F^E_{\mu, \sigma^2}$は、次のようになり一様分布に従います。
F_{\beta_{\hat M ,j},\sigma^2(X^T_{\hat M}X_{\hat M})^{-1}_{jj}}^{[ V^-(z),V^+(z)]}(\eta^Ty)
\sim
Unif[0,1]
そして、帰無仮説$\beta_{\hat M,j}=0$に対するSelective p-valueは次のように表現できます。
上記の累積分布関数からこのSelective p-valueは一様正規分布に従います。
p_{\hat M,j} = 1-F_{0,\sigma^2(X^T_{\hat M}X_{\hat M})^{-1}_{jj}}^{[ V^-(z),V^+(z)]}(\eta^Ty)
Selective confidence intervals(選択的な信頼区間)は$[ L_{\hat M ,j}, U_{\hat M ,j}]$は次を満たすような各点となります。
F_{L_{\hat M ,j},\sigma^2(X^T_{\hat M}X_{\hat M})^{-1}_{jj}}^{[ V^-(z),V^+(z)]}(\eta^Ty)=1-\frac{\alpha}{2}
F_{U_{\hat M ,j},\sigma^2(X^T_{\hat M}X_{\hat M})^{-1}_{jj}}^{[ V^-(z),V^+(z)]}(\eta^Ty)=\frac{\alpha}{2}
以上の切断正規分布のイメージは次のようになります。
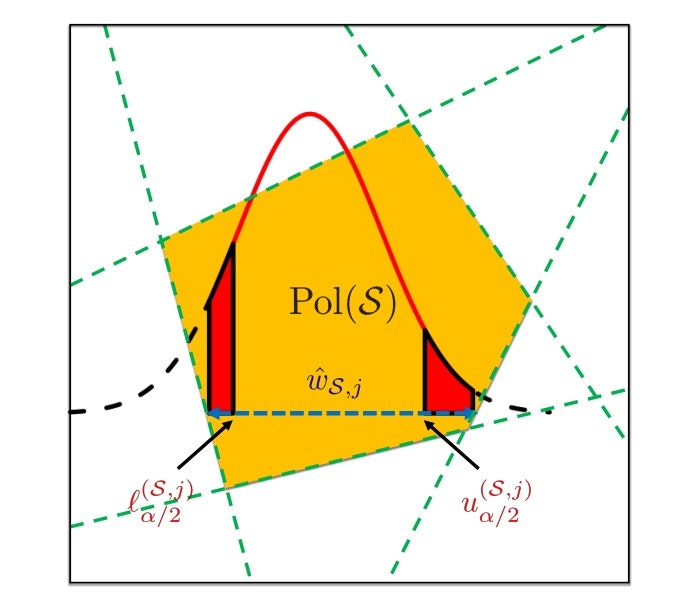
(出典)
最適なselective inferenceについて
selective inferenceにおける仮説を検定する際の、第1種の過誤(Selective type 1 error at lavel $\alpha$)は次のように表現できます。
E_{H_0}[\phi_q(X)|S_q]\leq\alpha
selective eventを条件付けた時の過誤を考えることを意味します。
ここで、条件付けの細かさを考えます。
条件の細かさとは、回帰分析では選択された変数やその変数の符号になります。
これを表現する変数:selective variable$V_q$とします。
$V_q$に関するSelective type 1 error at lavel $\alpha$は次にようになります。
E_{H_0}[\phi_q(X)|V_q]\leq\alpha
そして、細かい条件の集合$V_q^{(1)}$、荒い条件の$V_q^{(2)}$を考えます。
それぞれのSelective type 1 error at lavel $\alpha$は次になります。
E_{H_0}[\phi_q(X)|V_q^{(1)}]\leq\alpha \\
E_{H_0}[\phi_q(X)|V_q^{(2)}]\leq\alpha
条件付けは異なりますが、二つは同じ結果を得ます。
そのため、細かく条件付けしたselective inferenceを行えば、より粗く条件付けしたselective inferenceと同等の推定ができます。
そのため、lassoにおける選択イベントは、選択された仮説(偏回帰係数)に合わせてその符号で定義しています。
選択された仮説だけを条件付けた場合よりも細かい条件付けをしたselective inferenceがより少ないコストで行うことができます。
Rによるselective inference
Rでselective inferenceは、selectiveInferenceパッケージで推定することができます。
基本的なAICによる変数選択を行った際のselective inferenceは次のようになります。
set.seed(1234)
x = matrix(rnorm(n*p),n,p)
y = x%*%beta + sigma*rnorm(n)
gfit = fs(x,y)
out.seq = fsInf(gfit,type="aic",alpha = 0.05)
結果を見てみます。
見ての通りP-valueが回帰係数の統計的有意性を検定した結果になります。
> out.seq
Call:
fsInf(obj = gfit, alpha = 0.05, type = "aic")
Standard deviation of noise (specified or estimated) sigma = 0.457
Testing results at step = 6, with alpha = 0.050
Var Coef Z-score P-value LowConfPt UpConfPt LowTailArea UpTailArea
5 0.783 11.189 0.000 0.640 0.920 0.025 0.025
4 0.577 10.043 0.000 0.447 0.690 0.025 0.025
3 0.415 5.102 0.043 -0.074 0.592 0.025 0.024
1 0.406 5.295 0.000 0.260 0.879 0.025 0.025
2 0.178 2.627 0.117 -0.135 0.310 0.025 0.024
9 -0.131 -1.834 0.410 -0.381 0.503 0.025 0.025
Estimated stopping point from AIC rule = 6
ここで、上記で行なったものと同じ設定でバイアスのない推定が行えているかを確認してみます。
| $\beta_1$ | $\beta_2$ | $\beta_3$ | $\beta_4$ | $\beta_5$ | $\beta_6$ | $\beta_7$ | $\beta_8$ | $\beta_9$ | $\beta_{10}$ | |
|---|---|---|---|---|---|---|---|---|---|---|
| 棄却された数 | 1140 | 643 | 1430 | 1729 | 1771 | 24 | 26 | 24 | 21 | 23 |
| 棄却されたかった数 | 837 | 1107 | 570 | 272 | 230 | 356 | 352 | 339 | 327 | 331 |
| 選択されたかった回数 | 24 | 251 | 1 | 0 | 0 | 1621 | 1623 | 1638 | 1653 | 1647 |
概ね、5%程度の棄却率となっていると考えられます。
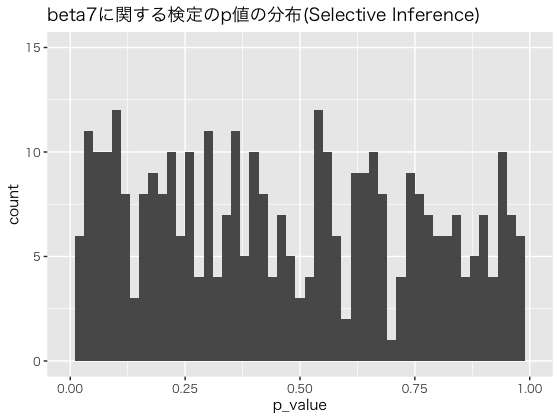
また、変数選択された場合のp値の分布を確認してみます。
一様分布に近い状態になっていることが確認できます。
結果としてバイアスのない推定が行われている状態に近づいたと考えられます。
次に、lassoにおけるselective inferenceをRで行います。
今回は正則化パラメータを0.3に固定して推定を行なってみました。
set.seed(42)
x = matrix(rnorm(n*p),n,p)
y = x%*%beta + sigma*rnorm(n)
gfit = glmnet(x,y)
lambda = .3
beta_ls = coef(gfit, s=lambda/n)[-1]
out = fixedLassoInf(x,y,beta_ls,lambda,sigma=sigma)
結果を確認してみます。
> out
Call:
fixedLassoInf(x = x, y = y, beta = beta_ls, lambda = lambda,
sigma = sigma)
Standard deviation of noise (specified or estimated) sigma = 0.500
Testing results at lambda = 0.300, with alpha = 0.100
Var Coef Z-score P-value LowConfPt UpConfPt LowTailArea UpTailArea
1 0.313 4.410 0.000 0.183 0.430 0.049 0.048
2 0.155 1.916 0.060 -0.011 0.290 0.049 0.048
3 0.280 3.491 0.001 0.145 0.414 0.048 0.048
4 0.836 9.338 0.000 0.595 0.982 0.049 0.050
5 0.907 11.136 0.000 0.636 1.038 0.050 0.049
6 -0.056 -0.752 0.484 -0.170 0.285 0.049 0.050
7 0.280 2.916 0.004 0.117 0.569 0.048 0.049
8 0.015 0.194 0.936 -3.149 0.026 0.050 0.049
9 -0.092 -1.098 0.506 -0.213 0.436 0.049 0.050
10 -0.130 -1.570 0.140 -0.273 0.077 0.049 0.049
Note: coefficients shown are partial regression coefficients
| $\beta_1$ | $\beta_2$ | $\beta_3$ | $\beta_4$ | $\beta_5$ | $\beta_6$ | $\beta_7$ | $\beta_8$ | $\beta_9$ | $\beta_{10}$ | |
|---|---|---|---|---|---|---|---|---|---|---|
| 棄却された数 | 1120 | 495 | 1604 | 1979 | 1997 | 30 | 31 | 33 | 29 | 37 |
| 棄却されたかった数 | 665 | 890 | 305 | 19 | 1 | 597 | 591 | 564 | 600 | 564 |
| 選択されたかった回数 | 18 | 198 | 1 | 0 | 0 | 1373 | 1378 | 1403 | 1371 | 1399 |
概ね5%になっており、バイアスのない推定ができていると考えられます。
教師なし学習のselective inference
真のクラスと異なるクラスタリングを行うと、各クラスに対して検定を行った場合、有意な差がない(検定の意味がない)場合でも有意な差があるという結果を導いてしまう可能性があります。
例えば、次のような状態です。
真のクラスタが1つの場合に間違って2つのクラスタがあるとしてしまうと、クラスタの特徴量に差があるかを検定すると差があると結論づけてしまう可能性があります。
 [(出典)](https://www.ieice.org/~sita/forum/article/2019/201903231310.pdf)
[(出典)](https://www.ieice.org/~sita/forum/article/2019/201903231310.pdf)
ポストクラスタリング推論
このようなクラスタリングにおけるバイアスもSelective inferenceを行うことで適切な推定ができるようになります。
この推定をポストクラスタリング推論とも呼びます。
K-meansのような非階層化ハードクラスタリングによりK個のクラスにデータが分けられた時の結果を次のように表現します。
\hat C:=\{\hat C_k\}_k^K
この時の検定統計量$s$は、2つのクラス$(k,k`)$の差があることを意味します。
s_{(\hat C_k,\hat C_{k`})} := \frac{1}{|\hat C_k|} \sum_{i\in\hat C_k}x_{ij}-\frac{1}{|\hat C_{k`}|} \sum_{i\in\hat C_{k`}}x_{ij}
データセット$X$に対するk-meansクラスタリングアルゴリズムを$A(X)$とすると、クラスタリングの逆像は次のようになります。
D:=\{X |\hat C←A(X)\}
イメージとしては次のような図です。
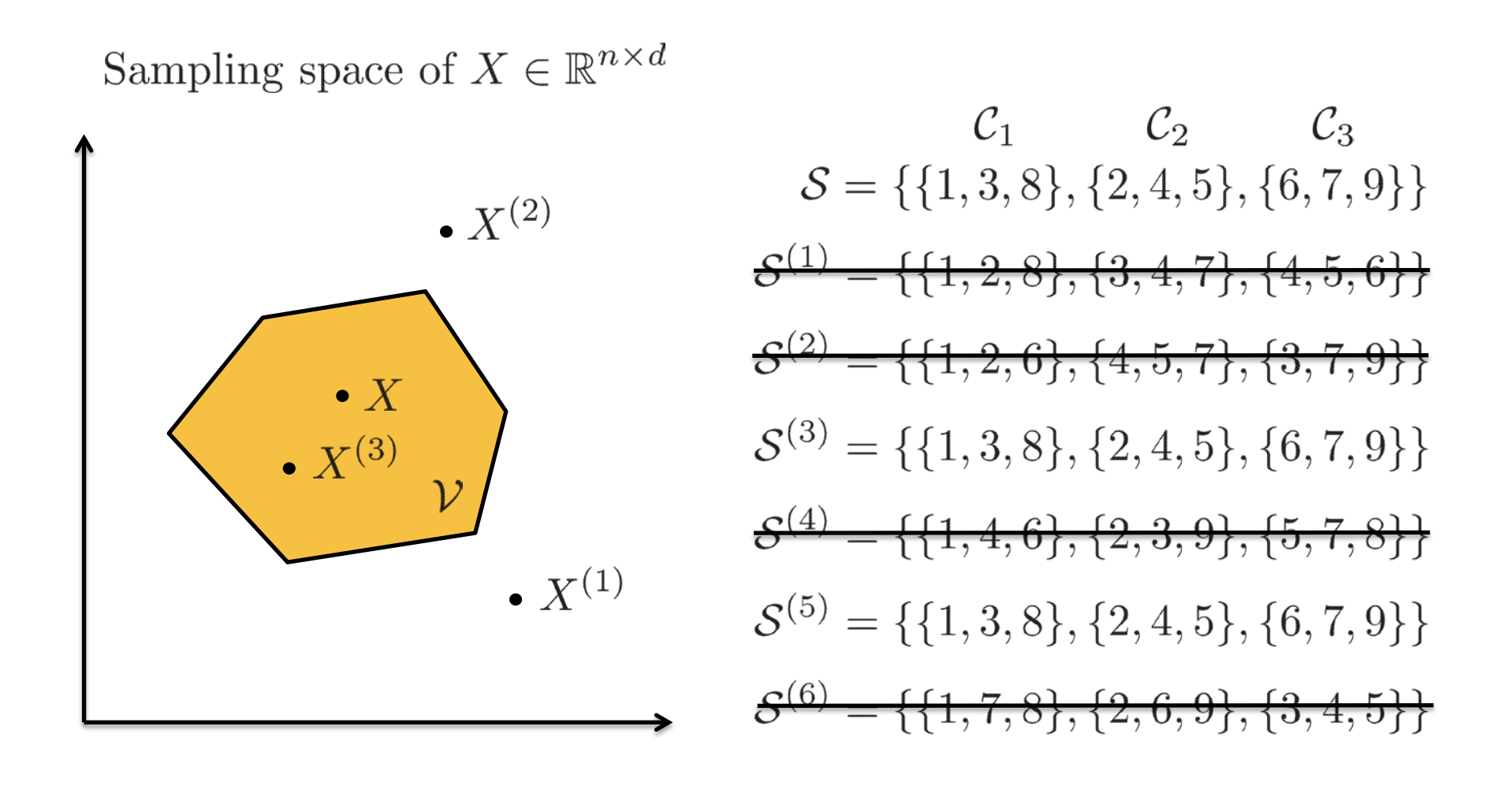
(出典)
回帰分析の時と同様にクラスタリングの逆像で条件付ければ、クラスタリングによるバイアスを覗くことができます。
逆像$D$を条件づけた時のクラスタリング時の仮説検定におけるselective inferenceは次のように表現することができます。
P(|x_{c_{i,j}}-x_{c_{i,j}}|\geq \theta | X \in D)<\alpha
ポスト階層型クラスタリング推論
帰無仮説の領域は、回帰分析の場合は線形な形で形成されます。
具体的には、偏回帰係数$\beta=0$のような一定値をとるという意味です。
一方で階層的クラスタリングにおける帰無仮説の領域は、仮説領域が非線形な形で形成されます。
そのため、階層的クラスタリングにおける、クラス間に差があるかの検定にはbootstrap法を用います。
この時、通常のbootstrap法ではリサンプリング数はサンプル数$n$に従います。
サンプル数$n$に寄らない様々な数でリサンプリングを行うmulti bootstrap法があります。
multi bootstrap法を用いることで不偏な推定できるとされています。
multi Bootstrap法を用いたselective inference
(ここまで、まとめようと思いましたが理解が追いついていません。詳しくはShimodaira (arXiv2017)を参考にしてください。)
RによるBoopstrap法 SI
Bootstrap法によるselective inferenceをRで行うにはpvclust(>Ver2.1)やscaleboot(>ver1.0)を用います。
両パッケージはCRANで公開されているものではバージョンが低く、最新の開発版を入れる必要があります。(2019年10月4日現在)
library(devtools)
install_github("shimo-lab/scaleboot", subdir = "src")
install_github("shimo-lab/pvclust", ref = "develop", subdir = "src")
用いるデータはpvclustパッケージに含まれるlungデータです。
このデータは肺腫瘍のDNAマイクロアレイデータであり、67肺腫瘍を含む73肺組織ごとに916の遺伝子が観察されたDNAマイクロアレイデータです。
コードは、下平先生の資料を参考にしました。
library(tidyverse)
library(pvclust)
library(parallel)
# 並列化のおまじない
cl <- makeCluster(detectCores())
data(lung)
n.pvclust = 10000
sa <- 9^seq(-1,1,length=13)
lung73.pvclust <- pvclust(lung, r=1/sa, nboot=n.pvclust, parallel=cl)
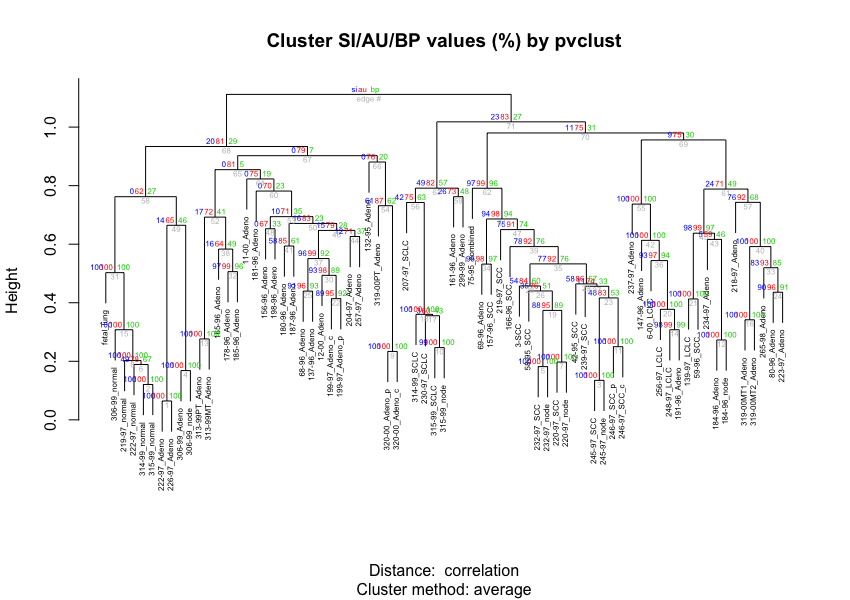
plot(lung73.pvclust, cex=0.5, cex.pv=0.5, offset=c(0.6,0.1,0.1,0.1))
各分岐点のに記載されている数字は、青がMulti Boostrap法によるselective inferenceの検定結果、赤はMulti Boostrap法による近似的に不偏な検定(approximately unbiased test:AU test)結果、緑はBootstrap法による検定結果です。
この値が0.95以上だと分岐するクラスター同士に有意な差がない=同一のクラスタに属すると考えられます。
いくつかのクラスタでAUの場合だと有意な差があるとされていても、SIの場合では有意な差がないと結論づけることができます。
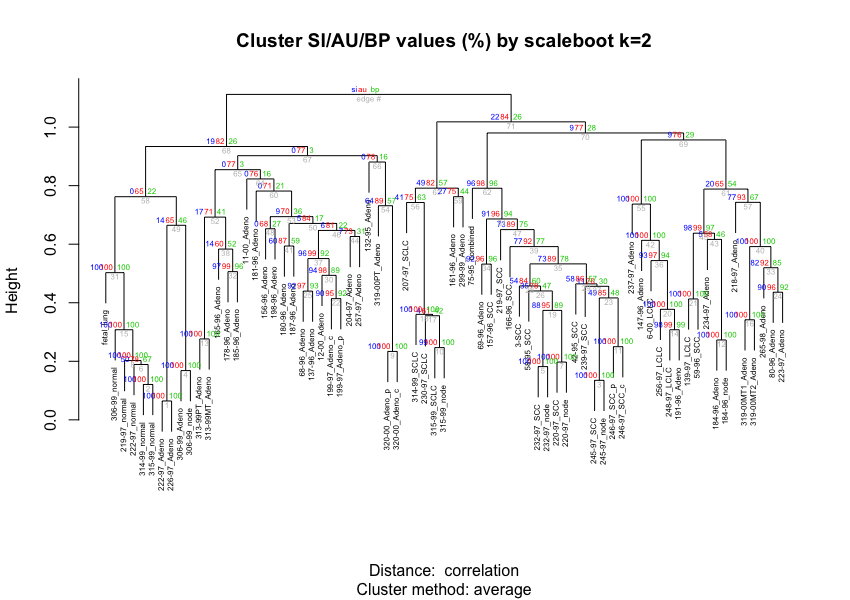
scalebootパッケージを用いた推定も行なってます。
pvclustの推定結果を用いて仮説領域をより滑らか推定し、より不偏(approximately unbiased)なselective inferenceが行えるようです。(後でもう少しちゃんと調べてみます)
library(scaleboot)
lung73.sb <- sbfit(lung73.pvclust,cluster=cl)
lung73.k2 <- sbpvclust(lung73.pvclust,lung73.sb, k=2)
結果を確認してみます。
> lung73.k2
Cluster method: average
Distance : correlation
Estimates on edges:
si au bp se.si se.au se.bp v c pchi
1 1.000 1.000 1.000 0.000 0.000 0.000 NA NA 0
2 1.000 1.000 1.000 0.000 0.000 0.000 -4.833 0.141 0
3 0.999 0.999 1.000 0.005 0.004 0.000 -4.643 -0.679 0
4 1.000 1.000 1.000 0.000 0.000 0.000 NA NA 0
5 0.999 0.999 1.000 0.004 0.003 0.000 -4.926 -0.479 0
6 0.497 0.783 0.669 0.010 0.006 0.005 -0.609 0.173 0
7 1.000 1.000 1.000 0.000 0.000 0.000 -5.601 -0.050 0
8 1.000 1.000 1.000 0.000 0.000 0.000 -3.900 0.044 0
9 1.000 1.000 1.000 0.000 0.000 0.000 NA NA 0
10 0.993 0.997 0.995 0.002 0.001 0.001 -2.659 0.055 0
11 1.000 1.000 1.000 0.000 0.000 0.000 -3.926 0.135 0
12 1.000 1.000 1.000 0.001 0.000 0.000 -5.584 -0.225 0
13 0.999 0.999 1.000 0.006 0.005 0.000 -4.848 -0.663 0
14 0.982 0.991 0.988 0.004 0.002 0.002 -2.315 0.065 0
15 1.000 1.000 1.000 0.000 0.000 0.000 -4.991 -0.044 0
16 0.999 1.000 1.000 0.001 0.000 0.000 -3.362 0.020 0
17 0.037 0.610 0.421 0.008 0.007 0.006 -0.039 0.240 0
18 1.000 1.000 1.000 0.002 0.001 0.000 -4.858 -0.537 0
19 0.882 0.951 0.892 0.010 0.005 0.004 -1.444 0.209 0
20 1.000 1.000 1.000 0.000 0.000 0.000 -5.108 -0.107 0
21 1.000 1.000 1.000 0.000 0.000 0.000 -4.730 0.190 0
22 0.896 0.954 0.920 0.011 0.006 0.004 -1.544 0.140 0
23 0.488 0.849 0.482 0.011 0.004 0.007 -0.493 0.538 0
24 0.904 0.959 0.915 0.009 0.005 0.004 -1.557 0.182 0
25 0.923 0.967 0.930 0.009 0.005 0.004 -1.659 0.186 0
26 0.348 0.783 0.468 0.011 0.005 0.007 -0.351 0.430 0
27 0.106 0.759 0.300 0.011 0.006 0.006 -0.089 0.613 0
28 0.543 0.838 0.596 0.009 0.005 0.004 -0.614 0.370 0
29 0.577 0.863 0.572 0.009 0.004 0.004 -0.637 0.455 0
30 0.939 0.979 0.888 0.007 0.003 0.004 -1.628 0.410 0
31 1.000 1.000 1.000 0.000 0.000 0.000 -4.261 -0.071 0
32 0.974 0.990 0.961 0.004 0.002 0.003 -2.046 0.283 0
33 0.819 0.923 0.852 0.012 0.006 0.004 -1.238 0.191 0
34 0.921 0.959 0.965 0.013 0.008 0.003 -1.778 -0.034 0
35 0.732 0.890 0.780 0.012 0.007 0.005 -1.001 0.227 0
36 0.933 0.971 0.942 0.008 0.004 0.003 -1.731 0.162 0
37 0.965 0.988 0.918 0.004 0.002 0.004 -1.830 0.436 0
38 0.137 0.603 0.524 0.008 0.008 0.005 -0.161 0.099 0
39 0.774 0.915 0.769 0.011 0.005 0.005 -1.054 0.319 0
40 0.999 1.000 0.998 0.000 0.000 0.001 -3.158 0.314 0
41 0.600 0.869 0.588 0.010 0.005 0.006 -0.673 0.450 0
42 0.999 1.000 0.998 0.000 0.000 0.000 -3.175 0.263 0
43 0.053 0.585 0.462 0.008 0.006 0.004 -0.060 0.155 0
44 0.070 0.733 0.308 0.016 0.006 0.006 -0.060 0.561 0
45 0.980 0.992 0.968 0.004 0.002 0.003 -2.132 0.284 0
46 0.061 0.807 0.218 0.019 0.006 0.006 -0.045 0.824 0
47 0.727 0.894 0.751 0.012 0.006 0.005 -0.963 0.286 0
48 0.000 0.683 0.274 0.000 0.007 0.006 0.063 0.539 0
49 0.140 0.654 0.460 0.008 0.006 0.004 -0.148 0.248 0
50 0.045 0.841 0.174 0.022 0.006 0.005 -0.031 0.968 0
51 0.913 0.960 0.941 0.012 0.006 0.003 -1.655 0.091 0
52 0.173 0.714 0.409 0.009 0.006 0.004 -0.168 0.398 0
53 0.093 0.699 0.364 0.009 0.007 0.005 -0.087 0.434 0
54 0.638 0.892 0.572 0.010 0.004 0.007 -0.709 0.527 0
55 0.998 0.999 0.995 0.001 0.000 0.001 -2.913 0.318 0
56 0.415 0.746 0.630 0.009 0.006 0.004 -0.496 0.165 0
57 0.768 0.929 0.673 0.010 0.004 0.005 -0.960 0.512 0
58 0.000 0.646 0.221 0.000 0.007 0.006 0.198 0.572 0
59 0.268 0.749 0.445 0.010 0.006 0.006 -0.267 0.406 0
60 0.000 0.713 0.207 0.000 0.006 0.006 0.127 0.690 0
61 0.205 0.645 0.541 0.008 0.008 0.005 -0.237 0.135 0
62 0.961 0.984 0.958 0.007 0.003 0.003 -1.936 0.207 0
63 0.493 0.819 0.571 0.009 0.005 0.004 -0.545 0.367 0
64 0.000 0.762 0.161 0.000 0.007 0.005 0.139 0.852 0
65 0.000 0.770 0.029 0.000 0.016 0.002 0.575 1.313 0
66 0.000 0.778 0.160 0.000 0.006 0.005 0.116 0.880 0
67 0.000 0.773 0.035 0.000 0.014 0.002 0.532 1.281 0
68 0.186 0.823 0.263 0.013 0.005 0.006 -0.146 0.779 0
69 0.091 0.756 0.294 0.010 0.006 0.005 -0.076 0.618 0
70 0.088 0.768 0.278 0.013 0.005 0.006 -0.071 0.661 0
71 0.219 0.840 0.257 0.012 0.005 0.006 -0.170 0.823 0
72 1.000 1.000 1.000 0.000 0.000 0.000 NA NA 0
plot(lung73.k2, cex=0.5, cex.pv=0.5, offset=c(0.6,0.1,0.1,0.1))
最後に
回帰分析で疑問に思っていた点が晴れてきた気がします。
絶対的に必要な手法ではないと考えられますが、分析を行う時の不安が解消するのに一役買ってくれそうです。
回帰分析を行う場合には、利用していきたいと思います。
ポスト階層型クラスタリング推論についてはこれから、きちんと勉強していきます。
参考
- http://www.jfssa.jp/taikai/2018/table/program_detail/pdf/-50/J10036.pdf
- http://statweb.stanford.edu/~tibs/ftp/lockharttalk.pdf?fbclid=IwAR2LnqeqDrZ_QVetKXjm_R9bGfQowrQUoSRTtZ-C0iquzby6bftQZ-4FWK0
- http://www.jfssa.jp/taikai/2018/table/program_detail/pdf/301-350/J10348.pdf
- https://arxiv.org/abs/1311.6238
- https://arxiv.org/abs/1905.10573
- https://www.ieice.org/~sita/forum/article/2019/201903231310.pdf
- http://stat.sys.i.kyoto-u.ac.jp/prog/pvclust/
- https://cran.r-project.org/web/packages/selectiveInference/selectiveInference.pdf
- http://ryamada22.hatenablog.jp/entry/20160228/1456616097
- http://joshualoftus.com/post/conditional-approach-to-inference-after-model-selection/
- http://www.sigmath.es.osaka-u.ac.jp/statmodel/wp-content/uploads/2017/08/terada.pdf
- http://langstat.hatenablog.com/entry/20140822/1408633200
- https://www.ism.ac.jp/editsec/toukei/pdf/50-1-033.pdf
- http://www.sigmath.es.osaka-u.ac.jp/statmodel/wp-content/uploads/2017/08/terada.pdf