はじめに
以前、潜在クラス分析について少しまとめました。(こちら)
今回は潜在クラスモデルの発展系である潜在クラスロジットモデルについてまとめました。
なお、こちらに記載していうRコードはGithubにあげています。
各マーケティング観点におけるモデリング
昔はメーカー主導の十人一色のマーケティングを行っていましたが、価値観が多様化するとともに、少数のグループごとにアプローチするようになっています。

(出典元)
この時、顧客/市場全体がターゲットの商品やブランドを購入する要因はどのようなものなのか、どのようなアプローチをすればいいのかという観点で用いるモデルがロジットモデルです。
一方、様々な要因から顧客のセグメンテーションを行い、各セグメントごとにロジットモデルを適用することで、各セグメントごとの購買行動の振る舞いの差を考慮したモデルを構築することができます。
このようセグメンテーションマーケティングに対応する考えのもとに成り立つモデルが、潜在クラスロジットモデルです。
また、one to oneマーケティングでは、各個人ごとに購入する要因を分析するためのモデルとして、ランダム係数ロジットモデル等が用いられます。
| マーケティング観点 | モデル |
|---|---|
| マスマーケティング | ロジットモデル |
| セグメンテーション マーケティング | 潜在クラスロジットモデル |
| one to one マーケティング | ランダム係数ロジットモデル |
潜在クラスモデル
潜在クラスモデルとは、観測された個体はいずれかの潜在クラスに属すると考えるモデルです。
ただし、どこか1つのクラスに決定してしまう(ハードクラスタリング)とみるのではなく、それぞれの潜在クラスに属する確率をもって表す(ソフトクラスタリング)ことになります。
対象のクラスの構成割合を見たり、説明変数による条件付き確率を見ることでクラスごとの差を比較することができます。
個体$i$(=1,...,n)から発生したデータ$y_i$について考えます。
個体$i$は観測されていない$C$個のクラス$c=1...g$に確率$\pi_c$で所属するとします。
この時、次式で表すような制約があります。
\sum_{c=1}^g\pi_c=1 (0<\pi_c<1)
この時の、クラス$c$に属する個人$i$の尤度は次のように表現します。
f_s(y_i|\theta_c ; x)
ここで、$x$は説明変数であり$\theta_c$は第$c$グループのK次元パラメーターベクトルです。
この時の次のような尤度で表すモデルが、潜在クラスモデルです。
L=f(y;\phi)= \prod_{i=1}^n \left\{ \sum_{c=1}^C \pi_c f_c(y_i|\theta_c;x) \right\}
潜在クラスロジットモデル
セグメント$s$においてユーザー$i$が時点$t$でブランド(商品)$j$を選んだ時$y_{itj}=1$,選ばなかった時を$y_{itj}=0$と表現します。
この確率をロジットモデルにより表現し、$P_s(y_{itj}=1)$とした時の、対数尤度を次のように表すことができます。
log L_{si} = \sum_{t=i}^T \sum_{j=1}^J y_{itj} log{P_s(y_{itj}=1)}
また、個人に関する対数尤度を次のように表現する。
\log L_c(\phi)=\log\left[\sum_{s=1}^S \pi_s \left\{ \prod_{i=1}^n \prod_{i=1}^n { P_s(y_{itj}=1)}^{z_{ic}} \right\} \right]
$\pi_s$はセグメント$s$の比率である。
ここで潜在クラス分析と同様に潜在変数$z_{is}$を用います。
セグメント$s$にユーザー$i$が所属している場合、$z_{is}=1$、それ以外は0となる。
完全データの対数尤度は次のようになり、$z_{ic}$は欠損値をしてEMアルゴリズムによりモデルの推定を行います。
\log L_c = \log\left\{ \prod_{i=1}^n \prod_{s=1}^S ({\pi_s L_{si}})^{z_{ic}}\right\}
= \sum_{i=1}^n \sum_{s=1}^S \{z_{is} \log L_{si} + z_{is} log \pi_s \}
ここで、$y_i$と$z_{is}$は独立であると仮定をおく。
Rで潜在クラスロジットモデル
Rでは有限混合分布モデルを扱うことができるflexmixパッケージがあります。
mlogitパッケージにあるケッチャプの購買データを対象に潜在クラスロジットモデルを当てはめてみようと思います。
はじめにデータの確認です。
それぞれのタイミングでの各ブランドのディスプレイや広告、価格の情報とその時に顧客が選択したブランドが記録されているデータです。
> library(tidyverse)
> library(mlogit)
> data(Catsup)
> head(Catsup)
id disp.heinz41 disp.heinz32 disp.heinz28 disp.hunts32 feat.heinz41 feat.heinz32 feat.heinz28 feat.hunts32
1 1 0 0 0 0 0 0 0 0
2 1 0 0 0 0 0 0 0 0
3 1 0 0 0 0 0 1 0 0
4 1 0 0 0 0 0 0 0 0
5 1 0 0 0 0 0 0 1 0
6 1 0 0 0 0 0 0 0 0
price.heinz41 price.heinz32 price.heinz28 price.hunts32 choice
1 4.6 3.7 5.2 3.4 heinz28
2 4.6 4.3 5.2 4.4 heinz28
3 4.6 2.5 4.6 4.8 heinz28
4 4.6 3.7 5.2 3.4 heinz28
5 4.6 3.0 4.6 4.8 heinz28
6 5.0 3.0 4.7 3.0 heinz28
モデルに当てはめるためにデータを加工します。
なかなかのクソコードです。
# 時間ステップの追加
Catsup <- Catsup %>%
mutate(t = seq_len(nrow(Catsup)))
# 変換の関数
tranceforme_catsup <- function(brand){
df <- Catsup %>%
select(id, contains(brand), choice, t) %>%
rename(display = starts_with("dis"),
price = starts_with("pri"),
feature = starts_with("fea")) %>%
mutate(brand = brand)
return(df)
}
Cdata <- Catsup$choice %>%
unique() %>%
as.character() %>%
map(tranceforme_catsup) %>%
bind_rows() %>%
mutate(choice = with(.,choice == brand))
# hunts32のブランド価値を0に設定
Cdata$brand <- relevel(factor(Cdata$brand), "hunts32")
そして、モデルの当てはめを行います。
クラスを1~10クラスと仮定したモデルを当てはめてそれぞれのモデルのAIC,BICを算出してもっとも当てはまりの良いモデルを求めます。
library(flexmix)
# いくつかのクラス数モデルを作成して当てはまりの良いクラス数を調べる
I <- 10
aic <- as.numeric(c())
bic <- as.numeric(c())
set.seed(42)
for(i in 1:I){
print(i)
tmp_model = flexmix(choice ~ display + feature + price + brand | id,
model = FLXMRcondlogit(strata = ~ t),
data = Cdata,
k = i)
#print(AIC(tmp_model))
aic[i] <- AIC(tmp_model)
bic[i] <- BIC(tmp_model)
}
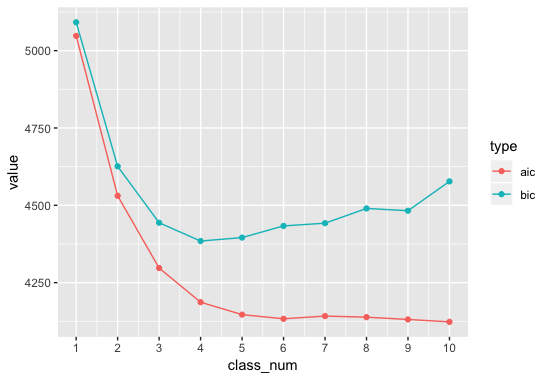
各クラス数における情報量基準をグラフ化してみましょう。
# グラフ作成
plot_data <- data.frame(class_num = c(1:I), aic, bic) %>%
gather(key = type, value = value, aic, bic)
gp <- ggplot(plot_data, aes(x = class_num, y = value, color = type)) +
geom_line() + geom_point() +
scale_x_continuous(breaks=seq(1,10,1))
gp
bic基準で4クラスモデルが最も当てはまりが良さそうです。
この時のモデルの分析結果をみてみたいと思います。
# BICが最小になるクラス数でモデル作成
LCLModel = flexmix(choice ~ display + feature + price + brand | id,
model = FLXMRcondlogit(strata = ~ t),
data = Cdata,
k = which.min(bic))
分析結果の確認
> summary(LCLModel)
Call:
flexmix(formula = choice ~ display + feature + price + brand |
id, data = Cdata, k = which.min(bic), model = FLXMRcondlogit(strata = ~t))
prior size post>0 ratio
Comp.1 0.398 5260 9004 0.584
Comp.2 0.161 1560 7040 0.222
Comp.3 0.307 3096 8484 0.365
Comp.4 0.134 1276 4092 0.312
'log Lik.' -2066.434 (df=27)
AIC: 4186.868 BIC: 4384.588
> parameters(LCLModel)
Comp.1 Comp.2 Comp.3 Comp.4
coef.display 1.7711567 0.4944214 0.4292297 1.01962258
coef.feature 0.8115368 1.1092501 1.4297427 1.60461416
coef.price -1.4114032 -2.2996486 -2.5506816 -0.05715993
coef.brandheinz28 3.3922350 0.4301673 4.4499172 2.89615288
coef.brandheinz32 3.9063956 -0.3919617 0.8994544 0.72212833
coef.brandheinz41 2.5852003 -0.1323809 2.6101961 2.05500074
グループ1は、ディスプレイ広告に影響されやすく、チラシ広告にあまり影響されないようです。
グループ2は、価格に影響されやすく、ブランドの銘柄に左右されないようです。
グループ3は、最も価格に影響されやすく、heinz28を好むようです。
グループ4は、最も価格に影響されず、チラシ広告に影響を受けるようです。
おわりに
サンプルデータで終わってしまいましたが、他のデータに適用して理解を深めていきたい感じがします。
あと、Stanでモデリングしたいですね。