最近ある研究会で潜在クラス分析が多用されてました。
潜在クラス分析の概要は理解していましたが、具体的な部分については理解していませんでした。
今後仕事等で利用するような場面が出てきそうな気がするので、ここでまとめておきたいと思いました。
潜在クラス分析の理論面の話とRによる実装を行っていきます。
潜在クラス分析
潜在クラスモデル
潜在クラスモデルとは、調査された個体は、いずれかの潜在クラスに属すると考えるモデルである。
ただし、どこか1つのクラスに決定してしまう(ハードクラスタリング)とみるのではなく、それぞれの潜在クラスに属する確率をもって表す(ソフトクラスタリング)ことになる。
対象のクラスの構成割合を見たり、説明変数による条件付き確率を見ることで回答のクラスごとの差を比較することができる。
個体$i$(=1,...,n)から発生したデータ$y_i$について考える。
個体$i$は観測されていない$C$個のクラス$c=1...g$に確率$\pi_c$で所属する。
この時、次式で表すような制約が存在する。
\sum_{c=1}^g\pi_c=1 (0<\pi_c<1)
この時の、クラス$c$に属する個人$i$の尤度は次のようになる。
f_s(y_i|\theta_c ; x)
ここで、$x$は説明変数であり$\theta_c$は第$c$グループのK次元パラメーターベクトルである。
この時の尤度を次式を表すことができる。
L=f(y;\phi)= \prod_{i=1}^n \left\{ \sum_{c=1}^C \pi_c f_c(y_i|\theta_c;x) \right\}
この尤度により考えられるモデルが、潜在クラスモデルである。
EMアルゴリズムによる推定
潜在クラスやパラメータの推定には、EMアルゴリズムによる最尤推定を行う。
最尤推定を行う際の対数尤度は次式になる。
\log L=\log f(y;\phi)= \sum_{i=1}^n \log \left\{ \sum_{c=1}^C \pi_c f_c(y_i|\theta_c;x) \right\}
E-step
EMアルゴリズムにより潜在クラスを求める場合に、潜在変数を考える。
この潜在変数は$i$がセグメント$s$に所属しているときは$z_{is}=1$、それ以外は0となる。
そして、$z_{ic}$は欠損値をしてEMアルゴリズムによりモデルの推定を行う。
完全データでは対数尤度$logL_c(\phi)$は次のようになる。
\log L_c(\phi)=\log\left[ \prod_{i=1}^n \prod_{i=1}^n {\pi_s f_s (y_i|\theta_s;x)}^{z_{ic}}\right] \\
= \sum_{i=1}^n \sum_{c=1}^C \{z_{ic} \log f_c(y_i|\theta_c;x) + z_{ic}\pi_s \}
M-step
M-stepで$\pi$,$\theta$の推定を行う。
制約下の推定を行うための、ラグランジュの未定乗数法による式を次のように表す。
\Lambda = \sum_{i=1}^n \sum_{c=1}^C \{\hat z_{ic} \log f_c(y_i|\theta_c;x) + \hat z_{ic}\pi_s \}-\lambda \left( \sum_{s=1}^g\pi_s=1\right)
$\Lambda$が最大になるような各パラメータを最尤推定により求める。
\lambda = n \\
\pi_c = \sum_{i=1}^n \frac{\hat z_{ic}}{n} \\
\hat \theta = \frac{\sum_{i=1}^n \hat z_{ic}(\sum_{t=1}^T y_{it})}{T\sum_{i=1}^n \hat
z_{ic}}
最後に$\pi_c$を事前確率としてベイズの定理を利用して事後確率を求めることができる。
\hat z_{ic} = \frac{\pi_c f_c (y_i| \theta_c x)}{\sum_{j=1}^g \pi_j f_j (y_i| \theta_j x)}
潜在クラス分析について
潜在クラス分析は、多項データに対し潜在クラスモデルを適用することでユーザーのセグメンテーションを行う分析である。
ユーザーの潜在的な思考の抽出や、潜在クラスの時間変化を見ることでユーザーの商品選択の思考の変化を捉えることでできるとされている。
消費者iがA,B,C,Dについて$(j,k,l,m)$を選択/回答したこと表す変数$x_{ijklm}$を考える。
選択した場合は$x_{ijklm}=1$、選択したかった場合は$x_{ijklm}=0$とする。
また、個別のカテゴリカル変数についても同様に、$x_{ij},x_{ik},x_{il},x_{im}$を定義する。
このような得られたデータ全体の尤度は次のようになる。
L=\prod_{i=1}^n \prod_{j=1}^J \prod_{k=1}^K \prod_{l=1}^L \prod_{m=1}^M (\pi_{jklm})^{x_{ijklm}}
ただし、次のような条件が存在する。
\sum_{i=1}^n \sum_{j=1}^J \sum_{k=1}^K \sum_{l=1}^L \sum_{m=1}^M \pi_{jklm}=1
次にg個の潜在クラスが存在すると考えると、$\pi_{jklm}$は次のようになる。
\pi_{jklm}=\sum_{c=1}^g \pi_c \pi_{jklm|c}
ここで、$\pi_c$は潜在クラスcの比率であり、$\pi_{jklm|c}$は潜在クラス$c$の条件付き選択確率である。
カテゴリカル変数は潜在クラスが与えられている下で独立であるとすると、$\pi_{jklm|c}$は次のように定義できる。
\pi_{jklm|c}=\theta_{jc}^A \theta_{kc}^B \theta_{lc}^C \theta_{mc}^D
$\theta_{jc}^A$は潜在クラス$c$における消費者のカテゴリカル変数$A$の第j番目の選択確率であり、他のカテゴリカル変数に置いても同様である。
そして、次の関係を満たす。
\sum_{j=1}^J \theta_{jc}^A=1
これら条件におけるモデルの各パラメータを推定する。
クラス数の決定方法について
モデルの適合度を測る指標として、AICとBICが挙げられている。
様々なクラス数の潜在クラスモデルを作成する。
各モデルにおけるAICやBICを算出し、最も適切なモデルにおけるクラス数を潜在クラスモデルのクラス数とする。
AIC = -2L +2d
BIC = -2L + d\log_e N
ここで$d$はパラメータ数であり、Nは対象者数である。
パラメータ数は今回説明したモデルにおける識別可能なパラメータ数は$J \times K \times L \times M-1$である。
この条件は潜在クラスモデルを用いた場合の識別可能なパラメータ数の最大値である。この条件は潜在クラスモデルを推定する場合の必要条件であり、次数条件と呼ぶ。
次に、パラメータの識別のための必要十分条件は顕在パラメータと潜在クラスパラメータ$\varPsi$に関する1次微分係数を要素とするヤコビアンの階数のもとで判断できる。
D= \left[ \frac{\partial \pi}{\partial \varPsi}\right]
Dの階数と潜在クラスのパラメーター数が等しい場合に局所的に判断可能である。
そのほかのモデルとの違い
因子分析は質的な変量をとる観測変数をグループ化するものである。
一方潜在クラス分析では、観測変数と潜在変数が両方ともカテゴリカル変数で個体/ユーザーをグループ化する。
また、クラス数の決定は主観的にしか行えないが、潜在クラス分析ではクラス数の推定が行える。
| 因子分析 | 潜在クラス分析 | |
|---|---|---|
| データの種類 | 量的データ | 質的データ |
| クラス数決定 | 主観で決定 | 定量的に決定 |
| グループ化対象 | 観測変数 | ユーザー |
Rによる実装
参考にしたテキストでは、EMアルゴリズムを実装するコードも紹介されていましたが、今回はpoLCAパッケージを利用してみました。
利用したデータセットはcarninomaで、子宮頚部に癌腫が存在するか否かについて、118患者に対する7人の病理学者による二分法の評価データです。
コードはbob3さんの記事から拝借しました。
> library(poLCA)
> data(carcinoma)
>
> f <- cbind(A,B,C,D,E,F,G)~1
> pol.aic <- numeric(6)
> pol.bic <- numeric(6)
> for (i in 1:6){
+ lca.model.tmp <- poLCA(f, carcinoma, nclass=i+1, maxiter=6000)
+ pol.aic[i] <- lca.model.tmp$aic
+ pol.bic[i] <- lca.model.tmp$bic
+ }
< 略 >
>
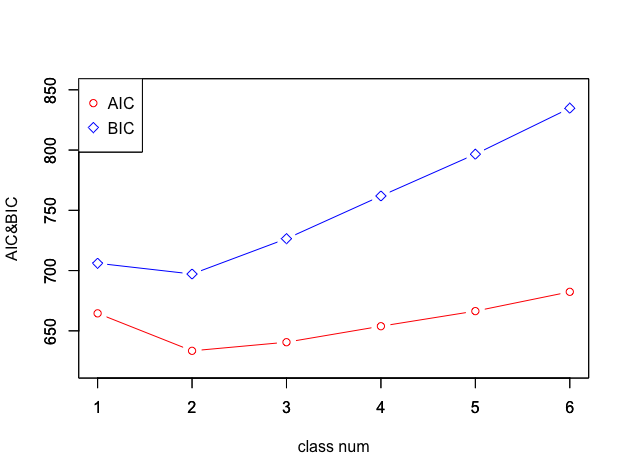
> # 結果のプロット
> plot(pol.aic, type="b", pch = 1, col = 2, ylim = c(620,850), xlab="", ylab="")
> par(new=T)
> plot(pol.bic, type="b", pch = 5, col = 4, ylim = c(620,850), xlab="class num", ylab="AIC&BIC")
> legend("topleft", legend = c("AIC","BIC"),col = c(2,4), pch = c(1,5))
両方の指標からクラス数は2が良さそうです。
クラス数2としたモデルを作成して結果を見てみます。
> # 最適なクラス数でモデルを作成
> lca.model<-poLCA(f, carcinoma, nclass=2, maxiter=6000)
Conditional item response (column) probabilities,
by outcome variable, for each class (row)
$A
Pr(1) Pr(2)
class 1: 0.8835 0.1165
class 2: 0.0000 1.0000
$B
Pr(1) Pr(2)
class 1: 0.6456 0.3544
class 2: 0.0169 0.9831
$C
Pr(1) Pr(2)
class 1: 1.0000 0.0000
class 2: 0.2391 0.7609
$D
Pr(1) Pr(2)
class 1: 1.0000 0.0000
class 2: 0.4589 0.5411
$E
Pr(1) Pr(2)
class 1: 0.7771 0.2229
class 2: 0.0214 0.9786
$F
Pr(1) Pr(2)
class 1: 1.0000 0.0000
class 2: 0.5773 0.4227
$G
Pr(1) Pr(2)
class 1: 0.8835 0.1165
class 2: 0.0000 1.0000
Estimated class population shares
0.4988 0.5012
Predicted class memberships (by modal posterior prob.)
0.5 0.5
=========================================================
Fit for 2 latent classes:
=========================================================
number of observations: 118
number of estimated parameters: 15
residual degrees of freedom: 103
maximum log-likelihood: -317.2568
AIC(2): 664.5137
BIC(2): 706.0739
G^2(2): 62.36543 (Likelihood ratio/deviance statistic)
X^2(2): 92.64814 (Chi-square goodness of fit)
標準誤差を出力して見ました。
> lca.model$probs.se
$A
[,1] [,2]
[1,] 4.509219e-02 4.509219e-02
[2,] 2.892112e-22 2.892153e-22
$B
[,1] [,2]
[1,] 0.08283463 0.08283463
[2,] 0.01706440 0.01706440
$C
[,1] [,2]
[1,] 0.00000000 0.00000000
[2,] 0.05886992 0.05886992
$D
[,1] [,2]
[1,] 2.821029e-116 2.821029e-116
[2,] 7.202397e-02 7.202397e-02
$E
[,1] [,2]
[1,] 0.06809304 0.06809304
[2,] 0.02163373 0.02163373
$F
[,1] [,2]
[1,] 0.00000000 0.00000000
[2,] 0.07078141 0.07078141
$G
[,1] [,2]
[1,] 5.151675e-02 0.05151675
[2,] 1.550076e-73 0.00000000
> lca.model$P.se
[1] 0.04633576 0.04633576
お試しだったため雑な感じに終わりますが、次は一から実装を行いたいと思います。
潜在クラス分析は色々な場面で使えそうですね。
個人的には潜在クラスの時間変化を見ていくような分析に興味があります。
参考
・里村卓也 著「 マーケティングモデル第二版」共立出版
・https://www.jstage.jst.go.jp/article/ojjams/24/2/24_2_345/_pdf
・http://bin.t.u-tokyo.ac.jp/kaken/pdf/2010_kokubun.pdf
・http://ides.hatenablog.com/entry/2017/06/21/145338