ご覧いただきありがとうございます。
過去の記事も含め、全てのコードをGithubで公開しています。
QiitaのTeXパーサーに問題があるのか、いくつか描画できない数式があったため、色々ごまかして工夫して描画させました。
不要な改行の挿入、全角のギリシャ文字を使用、ベクトル表記をせず普通の大文字で記述、添字の省略などは描画の代償ですのでスルーして頂ければ幸いです。
前編ではSimSiamの概要について説明しました。
SimSiamは「自己教師あり学習(Self-Supervised Learning)」(以下SSLと略します)の一種である「Non-Contrastive Learning」です。SimSiamはNon-Contrastive Learningで陥りがちな「崩壊(Collapse)」現象を以下の仕掛けによって回避しています:
- stop-gradient(勾配停止)
- predicator(予測器)
SimSiamの論文「Exploring Simple Siamese Representation Learning(シンプルなシャム表現学習の探究)[1]」では、残念ながら上記の仕掛けが崩壊(Collapse)を回避する理由までは解明していません。しかし、SimSiamが上記の仕掛けを使ってEMアルゴリズムのようなアルゴリズムを実現して損失関数を最小化しているのではないかとの「仮説(Hypothesis)」を立てています。この仮説は崩壊を防ぐメカニズムを直接説明するものではありませんが、少なくともこのシステムの振舞いについての説明になっています。
本記事ではこの論文の「仮説(Hypothesis)」の中身について解説します。仮説ではEMアルゴリズムのようなアルゴリズムとしてk平均法を想定しているので、まずk平均法について説明し、これと対比するかたちでSimSiamの振舞い、およびstop-gradient(勾配停止)、predicator(予測器)の役割について説明します。
1.k平均法クラスタリング(k-means clustering)
(1)EMアルゴリズムのようなアルゴリズムとは
論文[1]の第5章の冒頭に以下の記述があります:
Our hypothesis is that SimSiam is an implementation of an Expectation-Maximization (EM) like algorithm.
我々の仮説は、SimSiamはEM(Expectation-Maximization)のようなアルゴリズムの実装であるということです。
EMアルゴリズムそのものというよりはEMアルゴリズムのようなアルゴリズムを想定しているようですが、具体的にはどのようなアルゴリズムでしょう?さらに以下の記述があります:
This formulation is analogous to k-means clustering.
この定式化はK平均法クラスタリングに類似しています。
ということで、論文筆者はEMアルゴリズムのようなアルゴリズムとして「k平均法」(以下「k-means」と標記)を想定しているようです。k-meansはEMアルゴリズムの一種(混合分布モデルをハードクラスタリング化したもの)ですので、Eステップ、Mステップを交互に繰り返して最適化問題を漸進的に解くという程度の捉え方でよろしいかと思います。
のちにSimSiamのアルゴリズムをk-meansと対比的に説明するため、まずk-meansについて説明します。
k-meansはクラスタリングに用いられるごく一般的なアルゴリズムです。距離的に近そうなデータの塊にグループ分け(クラスタ分け)するというイメージです。例えば図1左図(クラスタリング前)では$x_1$~$x_6$の6個のデータが散らばっています。この6個のデータを2つのクラスタに分けるとすると、人間は簡単に分けることができますが、機械にはクラスタリングのためのアルゴリズムが必要となります。以下にそのアルゴリズムのステップを説明します。
図1:k平均法(k-means)の概要
(2)問題設定
問題を「$N$個の多次元ベクトル:${x_1, x_2, x_3, ... , x_N}$を$K$個のクラスタに分割する」と設定します。k-meansでは以下の評価関数を最小化するようにクラスタ分けを行います:
\mathcal{J}=\sum^N_{n=1}\sum^K_{k=1}r_{nk}\parallel x_n-\mu_k\parallel^2
| 記号 | 定義 | 説明 |
|---|---|---|
| $\mathcal{J}$ | 評価関数 | 「歪尺度」とも呼ばれる |
| $N$ | データ総数 | クラスタリング対象となるデータの総数 |
| $K$ | クラスタ総数 | クラスタリングの結果各データが属するクラスタの総数 |
| $x_n$ | データ | クラスタリング対称となる$n$番目のデータ,ここでは多次元ベクトルを想定 |
| $\mu_k$ | クラスタ代表点 | クラスタ$k$に属するデータの幾何中心(centroid) |
| $r_{nk}$ | データのクラスタ所属フラグ | データ$x_n$がクラスタ$k$に属する/属さないのフラグ |
この評価関数$\mathcal{J}$は$r_{nk}$と$\mu_k$の2つの変数を持ちます。評価関数の最小化は、一方の変数を固定して、もう一方の変数について最小化するステップを交互に繰り返す方針となります。
また、$r_{nk}$については、以下のように定式化されます:
r_{nk}=
\begin{cases}
{1 \ (x_nがクラスタkに属する)}\\
{0 \ (それ以外)}
\end{cases}
データ$x_n$がどのクラスタに属するかは以下の$K$次元ベクトル(通称「$r_n$ベクトル」とします)で表現できます:
[r_{n1}, r_{n2}, r_{n3}, ... , r_{nK}]
この$r_n$ベクトルの要素のうち1つだけが「1」となり、他の要素は「0」となります。これが論文中の以下の文章に現れる「one-hot-vector」に相当します:
The variable ηx is analogous to the assignment vector of the sample x (a one-hot vector in kmeans):
変数ηxはサンプルxの割り当てベクトル(k-meansにおける1-hotベクトル)に相当します。
(3)初期設定
クラスタ総数:$K$個のクラスタ代表点:$\mu_k$をデータ$x$のベクトル空間内にランダムに置きます。例えば図1中央図(クラスタリング開始)のようにクラスタ代表点を置きます。
(4)Eステップ: μ を固定して r について最小化
ここでやりたいことは、各データ$x_n$について、どのクラスタ代表点:$\mu_k$が一番近いか=どのクラスタに属するかを見つけることです。例えば図1中央図(クラスタリング開始)のように「$x_1$は$\mu_2$に一番近い」、「$x_2$は$\mu_1$に一番近い」というように全データについて調べていきます。
この操作は、クラスタ代表点:$\mu_k$を固定して、評価関数$\mathcal{J}$を最小にするような$r_n$ベクトルを見つけることを意味します。評価関数$\mathcal{J}$を単純に展開すると以下の式になります:
\mathcal{J}=\sum^N_{n=1}\{r_{n1}\parallel x_n-\mu_1\parallel^2+ ... +r_{nK}\parallel x_n-\mu_K\parallel^2\}
上式において{$r_{n1}$, ..., $r_{nK}$}のうち「1」の値はひとつだけで、それ以外は「0」となるので、評価関数$\mathcal{J}$を最小化するには{$\parallel x_n-\mu_1\parallel^2, ..., \parallel x_n-\mu_K\parallel^2$}のうち最小となるものをひとつ選べばよいことになります。もしも、$\parallel x_n-\mu_j\parallel^2$が最小であれば、$r_n$ベクトルの要素のうち$r_{nj}$のみが「1」となって、それ以外の要素は「0」になります。これは以下のように定式化されます:
r_{nk}=
\begin{cases}
{1 \ (k=\arg \min_j(\parallel x_n-\mu_j\parallel^2))}\\
{0 \ (それ以外)}
\end{cases}
この操作を$x_1$~$x_N$のすべてについて繰り返します。
(5)Mステップ: r を固定して μ について最小化
ここでやりたいことは、各クラスタ毎にクラスタ代表点:$\mu_k$を再計算することです。Eステップにて各クラスタにどのデータ:$x_n$が属しているかを計算済みなので、各クラスタに含まれているデータ:$x_n$の平均ベクトル(重心)を計算すれば、各クラスタ代表点:$\mu_k$を求めることができます。例えば図1中央図(クラスタリング開始)では、$\mu_1$で代表されるクラスタ(Cluster-1)はデータ「$x_2$, $x_3$, $x_6$」を含んでおり、この3ベクトルの平均ベクトル(重心)が新たなクラスタ代表点:$\mu_1$となります。
この操作は、$r_{nk}$を固定して、評価関数$\mathcal{J}$を最小にするようなクラスタ代表点:$\mu_k$を見つけることを意味します。評価関数$\mathcal{J}$を$\mu_k$で偏微分したものの値が0になるときの$\mu_k$が、評価関数$\mathcal{J}$を最小にする$\mu_k$となります。そして、その$\mu_k$が平均ベクトル(重心)であることを以下の式で導出します:
\begin{split}
\mathcal{J}&=\sum^N_{n=1}\{r_{n1}\parallel x_n-\mu_1\parallel^2+ ... +r_{nk}\parallel x_n-\mu_k\parallel^2... +r_{nK}\parallel x_n-\mu_K\parallel^2\}\\
\frac{\partial \mathcal{J}}{\partial \mu_k}&=\frac{\partial}{\partial \mu_k}\sum^N_{n=1}\{r_{n1}\parallel x_n-\mu_1\parallel^2+ ... +r_{nk}\parallel x_n-\mu_k\parallel^2... +r_{nK}\parallel x_n-\mu_K\parallel^2\}\\
&=\frac{\partial}{\partial \mu_k}\sum^N_{n=1}r_{nk}\parallel x_n-\mu_k\parallel^2\\
&=\frac{\partial}{\partial \mu_k}\sum^N_{n=1}r_{nk}\{x_n^Tx_n-2x_n^T\mu_k+{\mu_k}^T\mu_k\}\\
&=\sum^N_{n=1}r_{nk}\{-2\frac{\partial}{\partial \mu_k}x_n^T\mu_k+\frac{\partial}{\partial \mu_k}{\mu_k}^T\mu_k\}\\
&=\sum^N_{n=1}r_{nk}\{-2x_n+2\mu_k\}\\
\frac{\partial \mathcal{J}}{\partial \mu_k}=0&\Rightarrow \sum^N_{n=1}r_{nk}\{-2x_n+2\mu_k\}=0\\
&\Rightarrow \mu_k =\frac{\sum^N_{n=1}r_{nk}x_n}{\sum^N_{n=1}r_{nk}}\\
\end{split}
$\mu_1$~$\mu_K$のすべてについて上記平均ベクトル(重心)を計算します。
(6)停止
Eステップ、Mステップを繰り返し、クラスタ代表点:$\mu_k$の値に変化が無くなるとアルゴリズムは停止します。例えば図1右図(クラスタリング終了)のような状態となります。
2.SimSiam ~ 仮説(Hypothesis)
本章では、SimSiamの論文[1]の第5章「仮説(Hypothesis)」について解説します。まず、論文中では「SimSiamはEMアルゴリズムのようなアルゴリズムで学習しているのではないか」という仮説が述べられており、以下にそのアルゴリズムのステップを説明します。
(1)損失関数
まず、以下の損失関数$\mathcal{L}$を考えます:
\mathcal{L}(\theta, \eta) = \mathbb{E}_{x, \mathcal{T}}[\parallel \mathcal{F}_{\theta^t}(\mathcal{T}(x))-\eta_x \parallel^2]\\
| 記号 | 定義 | 説明 |
|---|---|---|
| $\mathcal{L}$ | 損失関数 | |
| $x$ | 入力画像データ | 例えば(sample, height, width, channel) のテンソルデータ |
| $\mathcal{T}()$ | 水増し画像生成器 | 画像データを入力として水増し画像データをランダムに生成する |
| $\mathcal{F}_{\theta^t}()$ | エンコーダ(ベクトル変換器) | 画像データをベクトルに変換する,$\theta^t$は時刻$t$での重みパラメータ |
| $\mathbb{E}_{x, \mathcal{T}}[]$ | 期待値 | 確率変数$x$および$\mathcal{T}$での期待値 |
| $\eta_x$ | 特徴ベクトル | 画像データ$x$の特徴表現≒特徴ベクトル |
損失関数$\mathcal{L}$の計算内容は、まず画像データ$x$を水増し画像生成器$\mathcal{T}$に入力して水増し画像データを得ます。次に水増し画像データをエンコーダ(ベクトル変換器)に入力してベクトルデータ:$\mathcal{F}_{\theta^t}(\mathcal{T}(x))$を得ます。一方、画像データ$x$を表現する特徴ベクトル:$\eta_x$をどこかから持ってきます。$\eta_x$は損失関数$\mathcal{L}$の入力変数(引数)みたいなものなので、エンコーダとかそのようなものとは無縁の別のところで計算されていても構いません。まあ、画像データ$x$を代表するようなベクトルなので、画像データ$x$を入力として何らかの計算はしているでしょうが。
次にベクトル:$\mathcal{F}_{\theta^t}(\mathcal{T}(x))$と、ベクトル:$\eta_x$のユークリッド距離を計算します。SimSiamの実装における損失関数としてはCosine Lossが用いられていますが、「仮説」では解析を容易にするためユークリッド距離とコサイン(Cosine)類似度を等価なものとみなして考察を進めています。
じつは、この損失関数$\mathcal{L}$は単発の距離計算だけでは終らず、$x$や$\mathcal{T}$を確率変数と見なした場合の期待値:$\mathbb{E}_{x, \mathcal{T}}[]$を計算することが必要になっています。どんな入力画像データを選ぶか、どんな水増し操作を施すかは確率的な要素ではあるのですが、損失関数に期待値を使うのは唐突かつ天下り的な感じではあります。
(2)問題設定
解きたい問題は損失関数$\mathcal{L}$を最小化することです。定式化すると以下の通り:
\min_{\theta, \eta}\mathcal{L}(\theta, \eta)\\
ここで大事なのは、損失関数$\mathcal{L}$が以下の変数$\eta$、$\theta$を引数としていることです:
- $\eta$:入力画像データの特徴ベクトル。上記最小化問題の引数だが何らかの方法で算出できる必要あり
- $\theta$:エンコーダ(ニューラルネットによるベクトル変換器)の重みパラメータ
この2変数を交互に少しずつ動かしながら損失関数$\mathcal{L}$が最小となるような$\eta$、$\theta$を求めます。図2は、この問題のシステム的な表現です:
図2:仮説のシステム的表現
ところで、この損失関数$\mathcal{L}$を最小にすると、結局何がどうなるのでしょう?ここからはまったくの私見ですので話半分に読んでください。
まず、この損失関数は入力画像データをエンコーダに通した出力ベクトル:$\mathcal{F}$θ $(\mathcal{T}(x))$と入力画像データの特徴ベクトル:$\eta_x$との距離を計っています。さらに、この損失関数は$\mathbb{E}_{x, \mathcal{T}}[]$で囲まれているので上記距離の期待値を計算しなければなりません。
したがって、入力される可能性のある画像データすべての上記距離の平均値(≒期待値)を最小化することが必要です。
上記距離を最小化する戦略を考えるにあたって、SimSiamはエンコーダを使う前提があることに留意します。エンコーダは入力データをベクトルへ変換し出力する仕組みです。したがって、エンコーダにできることは出力ベクトルを散らすか集めるかぐらいのことです。そうすると、まず入力画像データはグループ分け可能であることを前提として、エンコーダは学習によって入力画像データが属するグループ毎に固まるように出力ベクトルを配置することはできそうです。特徴ベクトルは何らかの方法で算出する必要はありますが、該当するグループの出力ベクトルの塊あたりに置くという仕組みを設ければ上記距離の最小化を図る一つの方法として考えられます。
また、エンコーダがグループ毎にベクトルの塊を作ることが可能であれば、どれかのグループに属する未知の画像データを入力しても正しいグループにベクトルを置くことが予想され、「期待値」も最小化されます。
以上より、損失関数$\mathcal{L}$を最小化することにより特徴ベクトルがグループ分けされることを期待してもよいかと思います。
(3)k-meansとの対比
SimSiamにおけるEステップ、Mステップをイメージするにあたって、k-meansにおけるEステップ、Mステップと対比することによってイメージが得られやすくなるかと思います。k-means、SimSiam(仮説)の式は各々以下のようにまとめられます:
k-means
評価関数: $\mathcal{J}(\mu,r) =\sum_n\sum_kr_{nk}\parallel x_n-\mu_k\parallel^2$
目的: $\min_{\mu, r}\mathcal{J}(\mu, r)$
Eステップ: $r^{t+1}\leftarrow\arg\min_r\mathcal{J}(\mu^t, r)$
Mステップ: $\mu^{t+1}\leftarrow\arg\min_\mu\mathcal{J}(\mu, r^{t+1})$
SimSiam(仮説)
評価関数: $\mathcal{L}(\theta, \eta)$ = $E_{x,T}$ $[\parallel \mathcal{F}_{\theta^t}(\mathcal{T}(x))-\eta_x \parallel^2]$
目的: $min_{\theta, \eta}\mathcal{L}(\theta, \eta)$
Eステップ: $\eta^{t+1}\leftarrow\arg\min_\eta\mathcal{L}(\theta^t, \eta)$
Mステップ: $\theta^{t+1}\leftarrow\arg\min_\theta\mathcal{L}(\theta, \eta^{t+1})$
また、論文中に以下の記述があります:
The variable θ is analogous to the clustering centers: it is the learnable parameters of an encoder. The variable ηx is analogous to the assignment vector of the sample x (a one-hot vector in kmeans):it is the representation of x.
変数θはクラスタリングセンタ(クラスタ代表点)に相当し、学習可能なエンコーダパラメータです。変数ηxはサンプルxの割り当てベクトル(kmeansでの1-hotベクトル)に相当し、これはxの代表ベクトルとなります。
つまり、両者の評価関数の2つの引数(パラメータ)は各々以下のように対応付けられます:
- 割り当てベクトル:$r$ → 特徴ベクトル:$\eta_x$
- クラスタ代表点:$\mu$ → エンコーダ重みパラメータ:$\theta$
上記の対応付けを横で眺めつつ、以下にSimSiam(仮説)のEステップ、Mステップについて説明します。
(4)Eステップ: θ を固定して η について最小化
このステップをk-meansで例えてみれば、全入力データがどのクラスタに属するか(=割り当てベクトル)を決定するステップでした。SimSiamでは画像データ$x$の特徴ベクトルを算出するステップとなります。具体的には以下の式を解きます:
\eta_x^{t+1}\leftarrow\arg\min_{\eta_x}\mathcal{L}(\theta^t, \eta_x)
また、この式は画像データ$x$毎に計算するので$x$は確率値ではなく確定値になるため、損失関数は確率変数$\mathcal{T}$のみの期待値となります。ここで確率変数$\mathcal{T}$の確率分布を$p(\mathcal{T})$と置き、エンコーダ重みパラメータ$\theta$を固定して、損失関数$\mathcal{L}$が最小となる(極値をとる)$\eta_x$を以下の式で求めます。
$\mathcal{T}$は本来、水増し画像生成関数としての記号ですがここでは確率変数と混同して用いています。論文でもそうなっているのでご勘弁を。
\begin{split}
\frac{\partial \mathcal{L}}{\partial \eta_x}&=
\frac{\partial}{\partial \eta_x}\mathbb{E}_\mathcal{T}[\parallel \mathcal{F}_{\theta^t}(\mathcal{T}(x))-\eta_x \parallel^2]\\
&=\frac{\partial}{\partial \eta_x}\sum_\mathcal{T}p(\mathcal{T})\parallel \mathcal{F}_{\theta^t}(\mathcal{T}(x))-\eta_x \parallel^2\\
\end{split}
ここで$z=\mathcal{F}_{\theta^t}(\mathcal{T}(x))$と置くと
\begin{split}
\frac{\partial \mathcal{L}}{\partial \eta_x}&=\frac{\partial}{\partial \eta_x}\sum_\mathcal{T}p(\mathcal{T})\parallel z-\eta_x \parallel^2\\
&=\frac{\partial}{\partial \eta_x}\sum_\mathcal{T}p(\mathcal{T})\{z^Tz-2z^T\eta_x+{\eta_x}^T\eta_x\}\\
&=\sum_\mathcal{T}p(\mathcal{T})\{-2\frac{\partial}{\partial \eta_x}z^T\eta_x+\frac{\partial}{\partial \eta_x}{\eta_x}^T\eta_x\}\\
&=\sum_\mathcal{T}p(\mathcal{T})\{-2z+2\eta_x\}\\
&=\sum_\mathcal{T}p(\mathcal{T})\{-2\mathcal{F}_{\theta^t}(\mathcal{T}(x))+2\eta_x\}\\
&=-2\sum_\mathcal{T}p(\mathcal{T})\{\mathcal{F}_{\theta^t}(\mathcal{T}(x))\}+2\eta_x\sum_\mathcal{T}p(\mathcal{T})\\
&=-2\mathbb{E}_\mathcal{T}[\mathcal{F}_{\theta^t}(\mathcal{T}(x))]+2\eta_x\\
\end{split}
上式では$\sum_\mathcal{T}p(\mathcal{T})=1$となることに注意。
\begin{split}
\frac{\partial \mathcal{L}}{\partial \eta_x}=0&\Rightarrow -2\mathbb{E}_\mathcal{T}[\mathcal{F}_{\theta^t}(\mathcal{T}(x))]+2\eta_x=0\\
&\Rightarrow \eta_x=\mathbb{E}_\mathcal{T}[\mathcal{F}_{\theta^t}(\mathcal{T}(x))]\\
\end{split}
結局、特徴ベクトル$\eta_x$は入力画像データ$x$についていろいろな水増し画像を生成し、その各々についてエンコーダを通し、出力されたベクトル群の平均ベクトルを計算すればよいということになります。これにより、「$\eta_x$を計算する何らかの仕組み」というのは水増し画像生成器とエンコーダを用いた仕組みということが予想できます。
(5)Mステップ: η を固定して θ について最小化
このステップをk-meansで例えてみれば、各グループ(クラスタ)のクラスタ代表点を計算するステップでした。SimSiamでは特徴ベクトル$\eta_x$を固定した上で損失関数が最小になるようにエンコーダの重みパラメータ$\theta$を調節します。これは以下のように定式化されます:
\theta^{t+1}\leftarrow\arg\min_\theta\mathcal{L}(\theta, \eta_x^{t+1})
エンコーダの重みパラメータ調節にはSGD(Stochastic Gradient Descent:確率的勾配降下法)を用います。このとき注意しなければならないのは、Mステップの計算時には$\eta_x$は定数として扱われるので、$\eta_x$側エンコーダ書き換えによる影響をバックプロパゲーション計算に反映させない仕掛けが必要となることです。それがstop-gradient(勾配停止)というわけです。
これにより、論文では「stop-gradient(勾配停止)の操作は当然の帰結である」と述べています。
(6)EステップとMステップを1ステップで実行する
ここでEステップとMステップを1ステップで実行する仕組みを考えます。まず、Eステップにおける特徴ベクトル$\eta_x$の計算の簡略化を試みます。Eステップでは$\eta_x$は以下のように計算されました:
\eta_x^{t+1} \leftarrow \mathbb{E}_\mathcal{T}[\mathcal{F}_{\theta^t}(\mathcal{T}(x))]
入力画像データ$x$から水増し画像をいくつかサンプリングし、エンコーダを通したベクトルの平均を求めるという手順でしたが、ここで近似手法として水増し画像を一つだけサンプリングするとします。サンプリングが一つしかないので期待値計算は無くなり、上式の$\mathbb{E}[]$が外れます。したがって以下の近似式で計算されます:
\eta_x^{t+1} \leftarrow \mathcal{F}_{\theta^t}(\mathcal{T'}(x))
ちなみに、論文ではEステップ側水増し画像生成器がMステップ側水増し画像生成器とは違う画像を出力することを意味するため$\mathcal{T'}$と標記しています。この式をMステップの式に代入すると以下の式が得られます:
\theta^{t+1}\leftarrow\arg\min_\theta\mathbb{E}_{x,\mathcal{T}}[\parallel \mathcal{F}_{\theta}(\mathcal{T}(x)) -\mathcal{F}_{\theta^t}(\mathcal{T'}(x))\parallel^2]
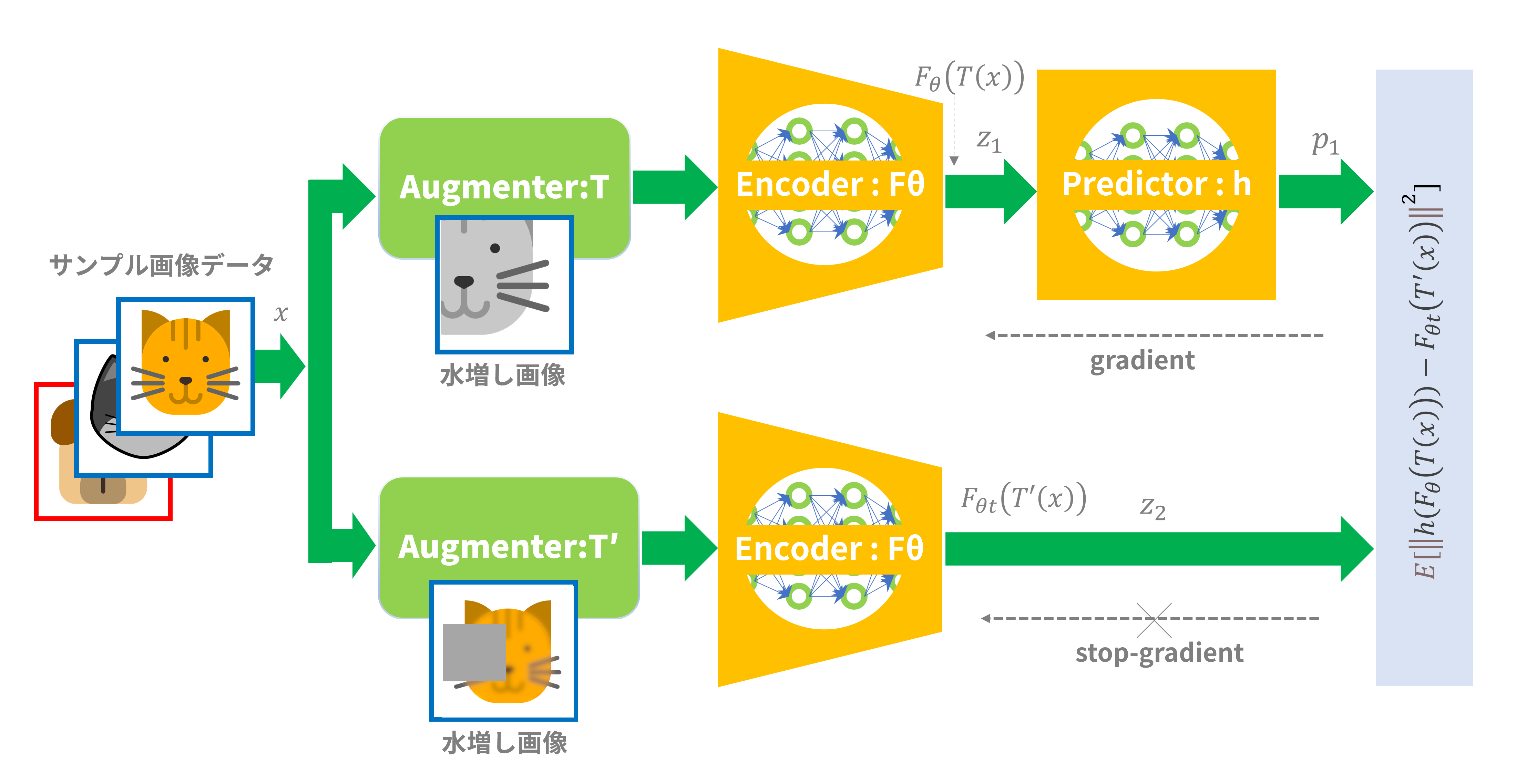
この式をシステム的に表現したのが図3です。これは、なんと、シャムアーキテクチャ(Siamese Architecture)になっているではありませんか!
図3:EステップとMステップを1ステップで実行する仕組み
(7)Predicator:h(予測器)
じつは図3のシステムではまだ「崩壊(Collapse)」を防ぐことはできません。図4に示すような「Predicator:h」の存在が必要です。Predictor:hは2層全結合型のニューラルネットワークで実装されています。
図4:Predicator:hの追加
では、このPredicator:hの役割は何でしょう?論文では以下のように記述されています:
In our approximation in (10), the expectation E[·] is ignored. The usage of h may fill this gap. In practice, it would be unrealistic to actually compute the expectation E[·]. But it may be possible for a neural network (e.g., the predictor h) to learn to predict the expectation, while the sampling of T is implicitly distributed across multiple epochs.
(10)の近似では、期待値E[-]は無視されます。 このギャップを埋めるのがhの使い道でしょう。実際には、期待値E[-]を本当にに計算することは非現実的でしょう。 しかし、ニューラルネットワーク(例えば、予測器h)は、Tのサンプリングが暗黙のうちに複数のエポックに分散されている間に、期待値を予測するように学習することは可能でしょう。
つまり1ステップ化で使用された$\eta_x$の計算式「$\eta_x^{t+1} \leftarrow \mathcal{F}_{\theta^t}(\mathcal{T'}(x))$」では期待値が無視されていることに問題があり、Predicator:hはそのギャップを埋めるものだと予想しています。
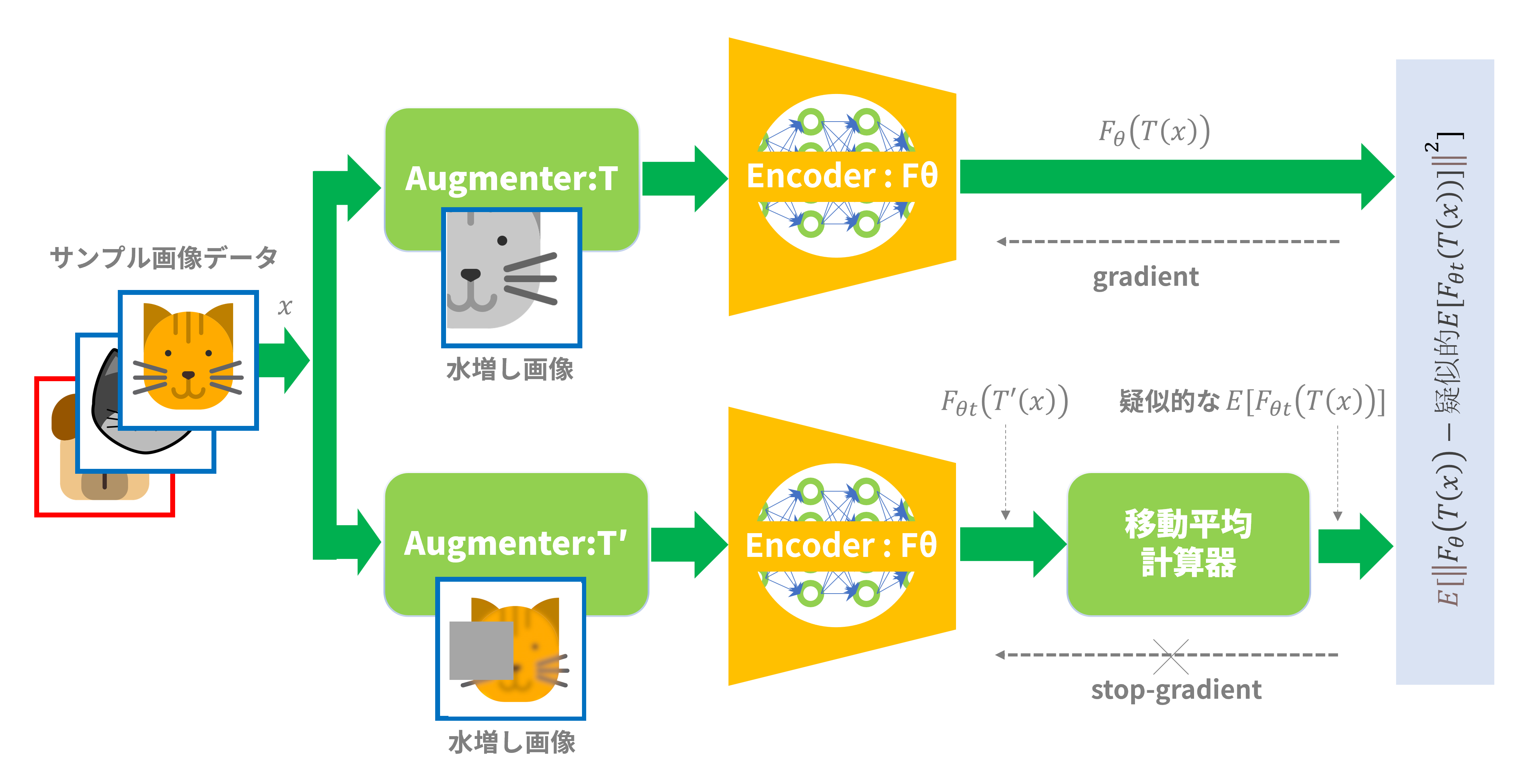
論文ではこの予想についての概念実証(Proof of Concept)実験を行っています。図5に示すように、対称形のシャムアーキテクチャ(Siamese Architecture)に加えて期待値計算に類するブロックを下側(stop-grandient側)のパスに挟むことで崩壊(Collapse)が回避されることを確認しています。
ちなみに「期待値に類する」計算として論文[1]では以下の移動平均計算を用いています:
\eta_x^{t+1}\leftarrow m*\eta_x^t+(1-m)*\mathcal{F}_{\theta^t}(\mathcal{T'}(x))
$m$はmomentum係数で、ここでは0.8を用いています。
図5:移動平均によるPoC
「なぜPredictor:hを移動平均計算器と同じ下側(stop-gradient側)のパスに置かないのか?」などいろいろ疑問はありますが、少なくとも期待値に関する計算ブロックを挟んだ非対称形のシャムアーキテクチャが崩壊(Collapse)を避けることができるとは言えそうです。Predictor:hもそのようなものの一種と言いたいところのようです。
この論文ではPredicator:hと期待値計算の関連を示唆するのみで終っていますが、じつはこのあたりの考察を深堀りした論文[2]もあり、詳しくはそちらを見たいところです。
3.まとめ
SimSiamは崩壊(Collapse)を回避するために以下の仕掛けを使っていました:
SimSiamは暗黙のうちに2つの変数セット($\eta$、$\theta$)を含み、各々の変数を交互に最適化するように振る舞うためにはstop-gradient(勾配停止)が必要となる。
変数$\eta_x$の計算には期待値計算が必要であり、Predicator(予測器)は単一サンプリングによる近似と期待値計算とのギャップを埋める。
この論文[1]は、とてもシンプルなやり方でうまくいっちゃいましたという報告っぽい感じで、「この仕掛けがなぜ崩壊(Collapse)を回避できるのか?」という疑問については直接的な答は無く、仮説(Hypothesis)による示唆に留めている印象です。このもやもやした部分を解決すべく、いくつかの論文が続いています。
まず、この論文の筆者(の一人)による論文[3] です。論文[3]では簡略化モデルを用いた理論的考察によって「なぜ崩壊しないのか?」の疑問に答え、勾配学習を行わず入力の統計量に基づいて線形予測器を直接設定する新しいアプローチDirectPredを提案しています。さらにその続編として論文[4]も出ています。
前章で紹介した論文[2]も「なぜ崩壊しないのか?」の疑問に答えた論文です。こちらはSimSiam論文[1]の主張を丁寧に再検討し、勾配解析においてベクトル分解による説明を試みています。
最後にSimSiamの確率的拡張を提案した論文[5]も挙げておきます。SimSiamの仮説ではいきなり損失関数に確率的要素を入れていましたが、もっときちんと確率的拡張を試みたものです。非対称アーキテクチャと変分推論(変分ベイズ)の間の理論的関係を明らかにして、表現の不確かさをうまく推定できるとしています。
上記論文は実際に精読したわけではないので、「なぜ崩壊(Collapse)を回避できるのか?」という疑問にビシッと答えられているのかは不明ですが、疑問が解決したら新たなネタとして紹介したいと思います。
参考文献:
[3] Understanding self-supervised Learning Dynamics without Contrastive Pairs
[4] Towards Demystifying Representation Learning with Non-contrastive Self-supervision
[5] Self-Supervised Representation Learning as Multimodal Variational Inference