ご覧いただきありがとうございます。ソリトンシステムズのセキュリティ分析チームです。
過去の記事も含め、全てのコードをGithubで公開しています。
以前のブログ記事「よくわかる深層系距離学習(前編/後編)」では「距離学習」に焦点を当てて解説しましたが、ここのところどうもこの分野は盛り上がっていないようです。面白いネタなのに何故?と思っていたのですが、最近「自己教師あり学習(Self-Supervised Learning)」とか「対照学習(Contrastive Learning)」というキーワードをやたら見かけるようになりました。さらに調べてみると、これらの手法を使って「教師なし学習」でありながら「教師あり学習」以上の性能を達成したとして最近おおいに盛り上がりを見せていることが判明しました。
本記事では自己教師あり学習(Self-Supervised Learning)の最新の成果である「SimSiam」の論文「Exploring Simple Siamese Representation Learning(シンプルなシャム表現学習の探究)[1]」について解説します。
1.簡単に用語を説明
論文の題名からして「?」という方のために、またSimSiamの立ち位置を説明するにはやたらと出てくる用語「なんとか学習」を理解する必要があるため、まず簡単に用語を説明しておきます。これらの用語を既にご存知の方は読み飛ばしてください。
(1)シャムネットワーク(Siamese Network)
論文の題名「シンプルなシャム表現学習の探究」のシャムはシャムネットワーク(Siamese Network)のことを指します。
シャム ネットワークは深層学習で用いられるニューラルネットワーク構成の一種で、同じネットワーク接続、同じ重みパラメーターを持つサブネットワークを対称的に配置した構造を持ちます。サブネットワーク各々がデータの入力口を持ち、各々の出力が比較されるようなかたちで損失関数が計算されます。図1はその典型例です。シャムネットワークは入力データの比較によってデータ間の関係性を学習し、例えば顔認識などの用途に使われます。
(2)表現学習(Representation Learning)
「表現学習」とはざっくり言って「タスクで使える解釈可能な特徴表現」を学習することです。例えば顔認識ならAさん、Bさん、Cさんを見分ける特徴表現を学習する。物体認識なら飛行機、車、鳥、猫、蛙を見分ける特徴表現を学習するといった塩梅です。特徴表現の典型的な例が「特徴ベクトル」です。以前のブログ記事で紹介した「距離学習」は「表現学習」の一種と捉えていいのかもしれません。
(3)自己教師あり学習(Self-Supervised Learning)
「自己教師あり学習」は英語では「Self-Supervised Learning」ですので以下「SSL」と略します。SSLは「教師なし学習(Unsupervised Learning)」の一種です。入力データそのものから教師データ(必要ならラベルも)を自動生成する学習手法ですので、人間が学習データにラベルを貼り付けるような作業は必要ありません。「教師あり学習(Supervised Learning)」においてラベル付きの教師データを人力で大量に用意するのは大変なコストになるので、そのコストがないSSLは非常に魅力的です。しかも、その性能が教師あり学習にも劣らないとなれば注目せざるを得ません。
(4)対照学習(Contrastive Learning)
基本的にはシャムネットワーク(Siamese Network)のようなアーキテクチャを持ち、サンプルペアを同時に入力します。そして、特徴空間において類似したサンプルペアが互いに近くにあり、異なるサンプルペアが遠く離れているような特徴表現を学習します。
例えばクラス分類が目的なら以下のような学習をします:
- サンプルペアが同じクラスに属するならば特徴ベクトルを近づける
- サンプルペアが異なるクラスに属するならば特徴ベクトルを遠ざける
対照学習(Contrastive Learning)は教師あり学習にも、教師なし学習にも古くから使われています[2]。
しかし、ここのところSSL界隈で用いられているContrastive Learning系の手法が大きな成果をあげているため、Contrastive Learning系の手法と言えば、SSLの一手法としてとらえられがちです。本記事のネタ「SimSiam[1]」もその範疇に入り、類似した手法で有名どころとしては「SimCLR[3]」、「SwAV[4]」、「BYOL[5]」等々が挙げられます[6]。
参考文献:
[2] Contrastive Representation Learning
[3] A Simple Framework for Contrastive Learning of Visual Representations
[4] Unsupervised Learning of Visual Features by Contrasting Cluster Assignments
[5] Bootstrap your own latent: A new approach to self-supervised Learning
[6] A Survey on Contrastive Self-supervised Learning
2.教師あり学習におけるContrastive Learning
SimSiamは「教師なし学習におけるContrastive Learning」系の手法なので、その対比として「教師あり学習におけるContrastive Learning」の手法をまず説明します。その後、教師あり学習との違いを通じてSimSiamの説明をしたいと思います。
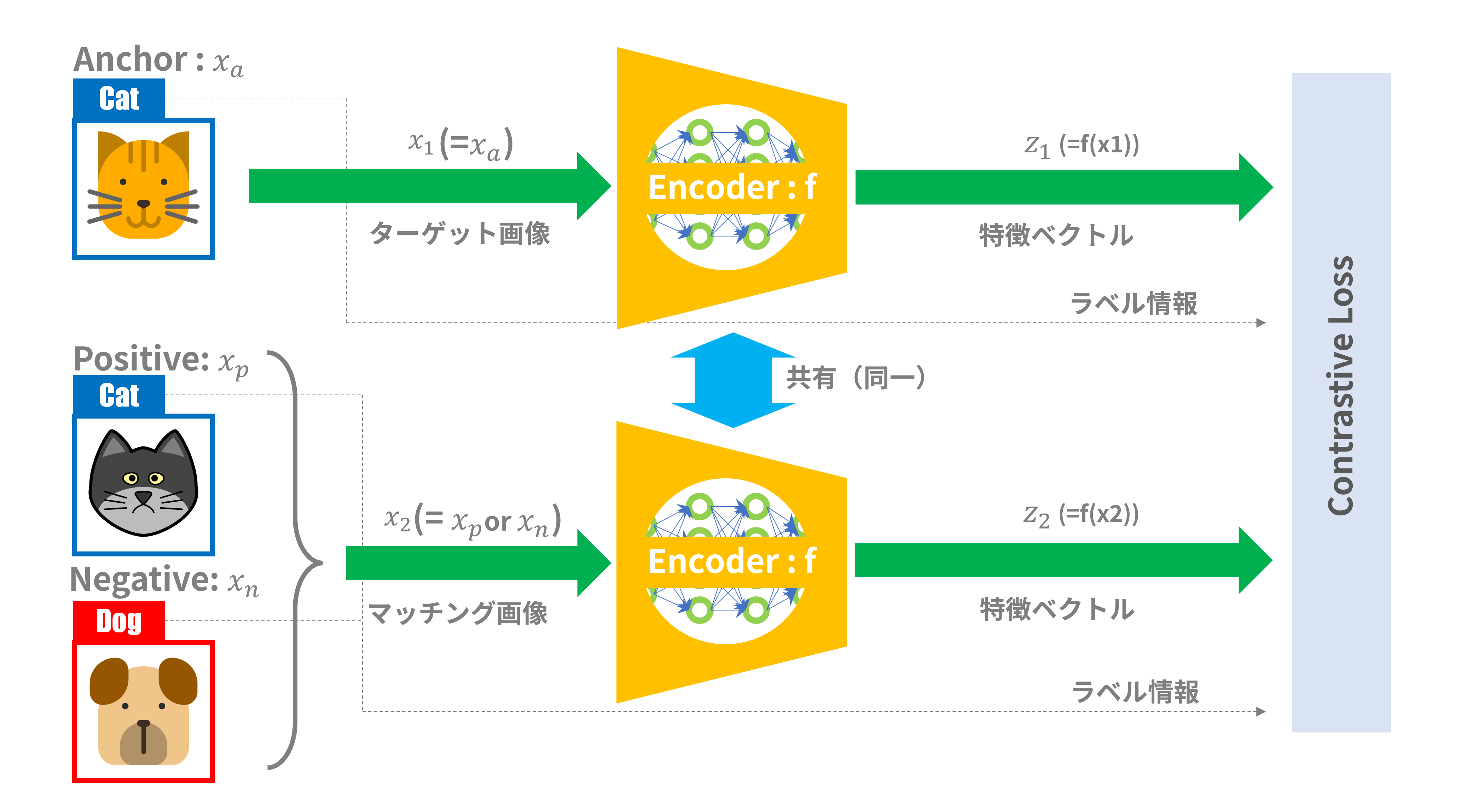
教師あり学習での有名どころとして2005年に発表された「Contrastive Loss」による深層距離学習[7]が初期の代表例として挙げられます。以前の記事で取り上げたFaceNet(Trilplet Loss)の基になった手法ですね。図1がこの手法の説明図です:
図1:「Contrastive Loss」による深層距離学習
(1)入力画像
用意されたサンプル画像から以下のペアを選び出します:
- 同じラベルのペア(Anchor - Positive)
- 異なるラベルのペア(Anchor - Negative)
ラベル名「Cat」のとある猫の画像を「Anchor」画像(ターゲット画像)とすれば、その対となる画像(マッチング画像)として、ラベル名「Cat」ではあるが違う猫の画像であれば「Positive」画像と呼ばれます。逆に、ラベル名「Dog」の画像であれば(つまりラベル名「Cat」以外の写真であれば)なんでも「Negative」画像と呼ばれます。
サンプル画像へのラベル情報の添付や、サンプル画像ペアの選出は学習の前に準備しておかなければなりません。
(2)アーキテクチャ
いわゆるシャムネットワーク(Siamese Network)構成です。図1のエンコーダ「Encoder:f」は入力として画像データ(テンソル)、出力としては特徴ベクトルとなります。以前の記事に載せた「ベクトル変換器」に該当します。たいていは畳み込みニューラルネットワーク(CNN:Convolutional Neural Network)で実装されます。
エンコーダは同じもの(共通の重みパラメータを持つニューラルネット)が2つ対照的に配置され、ターゲット画像:$x_1$として「Anchor」画像、マッチング画像:$x_2$として「Positive」画像または「Negative」画像が入力されます。各々のEncoderに入力された画像データは特徴ベクトル$z_1$、$z_2$に変換され、ラベル情報と共に損失関数へ送られます。
(3)損失関数
この手法での損失関数「Contrastive Loss」は以下の式で表されます:
\mathcal{L}_{contrastive}=\frac{1}{2}YD^2+\frac{1}{2}(1-Y)max(margin-D,0)^2\\
D=||f(x_1)-f(x_2)||_2\\
Y=
\begin{cases}
{0 \ (if\ x_2\ is\ negative\ sample)}\\
{1 \ (if\ x_2\ is\ positive \ sample)}
\end{cases}
上式では$f(x_1)$、$f(x_2)$は図1の$z_1$、$z_2$を意味します。距離$D$は特徴ベクトル$z_1$、$z_2$のユークリッド距離です。「Contrastive Loss」を用いて、サンプルペアが同じクラスに属する(Positive)ならば特徴ベクトルを近づける、サンプルペアが異なるクラスに属する(Negative)ならば特徴ベクトルを遠ざけるように学習が進むので、ラベル情報$Y$の値「0/1」で距離の計算式を切り分けています。
この手法では損失関数としてユークリッド距離を用いていますが、角度系距離=ベクトルの内積を使って損失計算式を構成するものも多数あります(と言うかそちらの方が主流か)[2]。
(4)学習
学習時は、バックプロパゲーションによって両方のエンコーダの重みパラメータが更新されます。重みパラメータは「Contrastive Loss」が減少するように更新されます。
参考文献:
[7] Learning a Similarity Metric Discriminatively, with Application to Face Verification
3.SimSiamの概要
SimSiam[1]は、自己教師あり学習(SSL)の一種であり、比較的新しめの手法です。この手法のすごいところは、Negativeのサンプルデータを使うことなしに、シンプルなアーキテクチャで高い正解率を持つエンコーダの学習が可能だということです。Negativeのサンプルデータを使わずPositiveのサンプルデータのみを使うということは、「対照的(contrastive)な学習」ではないということで「Non-Contrastive Learning」とも呼ばれているようです。そうは言ってもシャムネットワーク型のアーキテクチャであることから「Contrastive Learning」の一種と分類されるのも一般的で、なんとも混乱を招くところではあります。
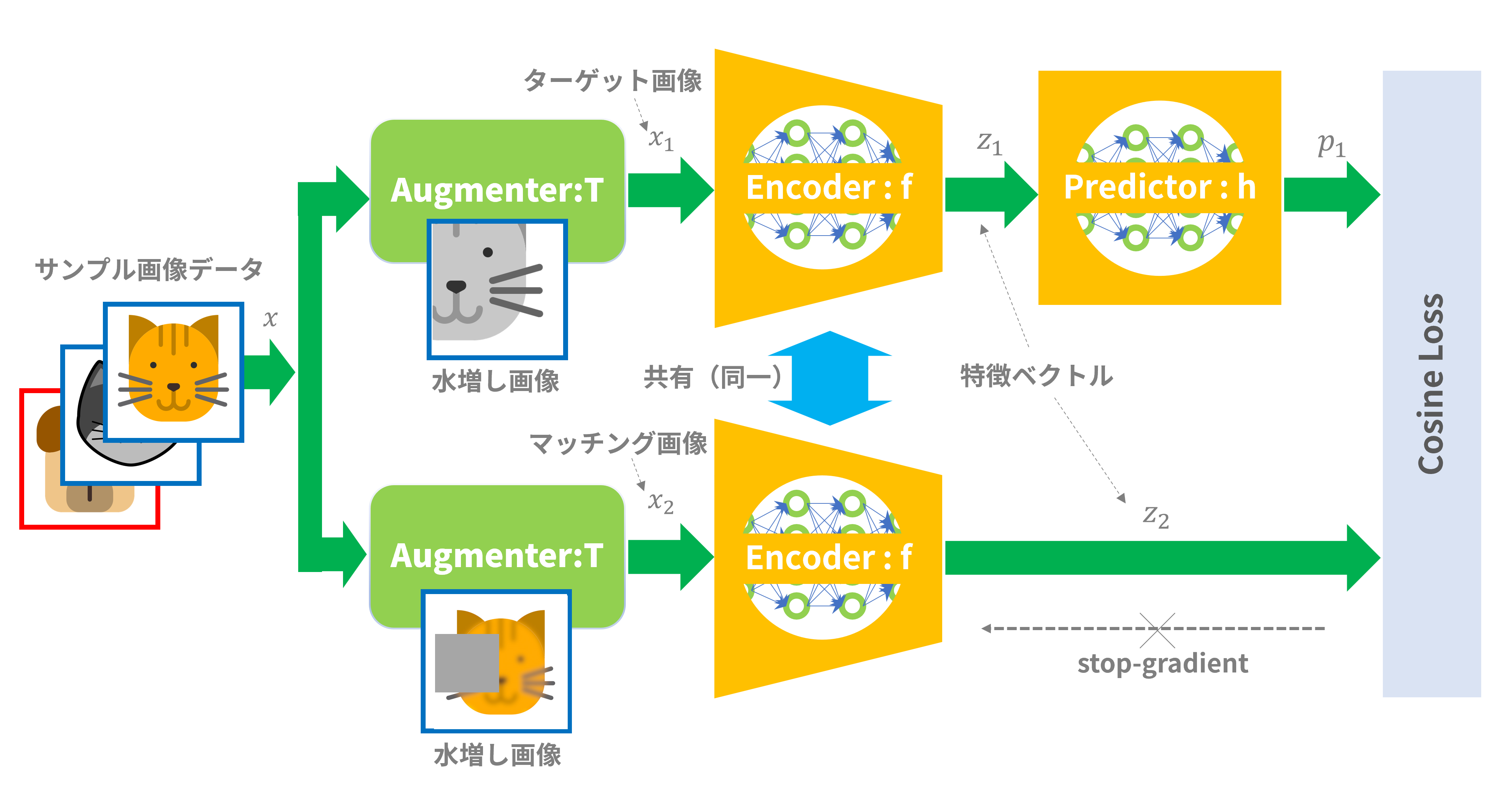
図2はSimSiamの説明図です:
図2:SimSiamの概要
(1)入力画像
サンプル画像データのラベル付けは必要ありません。マッチング画像をNegative、Poisitiveに分ける必要もありません。淡々とサンプル画像をシステムに放り込むだけです。
システムでは、受け取ったサンプル画像を「Augmenter:T」すなわち「水増し(Augmentation)画像生成器」に入力します。
「水増し画像生成器」では受け取った画像に以下の処理を施します:
- 画像の一部をランダムな位置・サイズでトリミングし、希望のサイズに拡大・縮小する
- 画像を水平方向に反転する
- 画像の明るさ、コントラスト、彩度、色相を変更する
- 画像の一部をランダムにグレーアウトする
- 画像をガウスカーネルによりぼかす
どの処理を選択するか、位置やサイズ、効果の程度等々、諸々のパラメータはランダムに決定され、サンプル画像を入力するたびに異なる画像が出力されます。したがって、一枚のサンプル画像が投入されるたびに、Anchor画像:$x_1$、Positive画像:$x_2$が自動的に生成されます。この仕組みによって、SimSiamが「自己教師あり学習(Self-Supervised Learning:SSL)の一種に分類される所以(ゆえん)となります。「水増し画像生成器」は同じ画像でも入力する度に異なる画像を出力するので、ここで確率的な要素が加わることにも留意してください。
(2)アーキテクチャ
基本的にはシャムネットワーク構成ですが、以下の点が前述の「Contrastive Loss」による深層距離学習の例と異なります:
- エンコーダ「Encoder:f」の前段に水増し画像生成器「Augmenter:T」が入る
- ターゲット画像側(図2では上側)のエンコーダ「Encoder:f」の後段($z_1$)にのみ予測器「Predictor:h」が入る
水増し画像生成器「Augmenter:T」については前述の通りです。予測器「Predicator:h」は全結合(Full Connection)層で構成されたニューラルネットワークで、ベクトル$z_1$から同次元のベクト$p_1(=h(z_1))$へ変換します。この予測器「Predictor:h」はSimSiamにとってなくてはならないブロックです。何を「予測」するかについては後編にて説明の予定です。
(3)損失関数
SimSiamの損失関数は単純なコサイン・ロス(Cosine Loss)です。ベクトル$p_1$もベクトル$z_2$も長さを正規化(つまり長さ=1)しています。正規化されたベクトル同士の内積は$cos \theta$(ただし$\theta$はベクトル同士の成す角度)となります。$\theta$が小さくなる(つまり「近付く」)ほど損失関数値は小さくなります(先頭にマイナスがあるから)。
$$
\mathcal{L}_{simsiam}=-\frac{p_1}{||p_1||}\cdot\frac{z_2}{||z_2||}\
$$
SimSiamの論文[1]ではもう少し複雑な損失関数になっていますが、本質的には上記の損失関数の組み合わせとなります。
(4)学習
学習時は、バックプロパゲーションによってターゲット画像側(図2では上側)のエンコーダの重みパラメータのみが更新されます。マッチング画像側(図2では下側)のエンコーダの重みパラメータは更新されません。バックプロパゲーション計算時に重みパラメータを更新しないこと(偏微分計算時に重みパラメータを定数として扱う)を勾配停止:「stop-gradient」と呼び、これがSimSiamの大きな(重要な)特徴となります。
4.Non-Contrastive Learningの弱点とSimSiamでの対策
SimSiamはNon-Contastive Learningの一種ですが、一般的にNon-Contastive Learningにはある弱点があります。
Non-Contrastive Learning はマッチング画像としてPositive画像しか使わないので、Negative画像を遠避けるという計算は含まれていません。したがって、学習時にはターゲット画像とマッチング画像をひたすら近付けることのみを目標とします。損失関数を最小にする一番安易な方法は、エンコーダがどんな画像を入力されても固定した値(つまり定数)を持つ特徴ベクトルを出力することです。特徴ベクトルが定数ベクトル(ゼロベクトルも含む)になるならば特徴ベクトル同士の角度は常にゼロとなるので損失関数は常に最小になります。
しかし、このような特殊な特徴ベクトルは望まれた結果ではなく、連立方程式の自明解みたいなものです。学習の結果、このような特徴ベクトルが得られることを「崩壊(Collapse)」と呼びます。Non-Contrastive Learningではこのような崩壊に陥りやすく、崩壊をどう防ぐかが方式設計のポイントとなっているようです。
SimSiamは以下の工夫で、Non-Contastive Learningの弱点である「崩壊(Collapse)」を防いでいます:
- ターゲット画像側(図2上側)のエンコーダの後段($z_1$)にのみ予測器「Predictor:h」を入れる
- バックプロパゲーション計算時にマッチング画像側(図2下側)のエンコーダに対して勾配停止(Stop-Gradient)する
SimSiamの論文[1]によれば、上記2点のいずれが欠けても容易に崩壊状態に陥ることが示されています。上記2点はSimSiamを構成するうえでの非常に重要な特徴です。
ちなみに、「Negative画像を遠避ける」という計算を含むContrastive Learningは、崩壊には陥りにくいと言われています。
5.学習結果の利用方法
自己教師あり学習(SSL)での学習結果を実際にどのように利用すればよいでしょうか。
まず実現したいタスクを以下の2つのタスクに分解します:
- Pretext Task:実現したいタスクに有効な特徴表現を得る疑似的なタスク
- Target Task:Pretext Taskの結果(特徴表現)を使ってやりたいことを直接的に実現するタスク
SSLはまさに「Pretext Task」に相当します。SSLでの学習結果として得られたエンコーダ(図2の「Encoder:f」)は「ベクトル変換器」であり、これによって特徴表現を得ることができます。例えば入力画像が「猫」なら猫の特徴ベクトル、「犬」なら犬の特徴ベクトルを得ることができます。
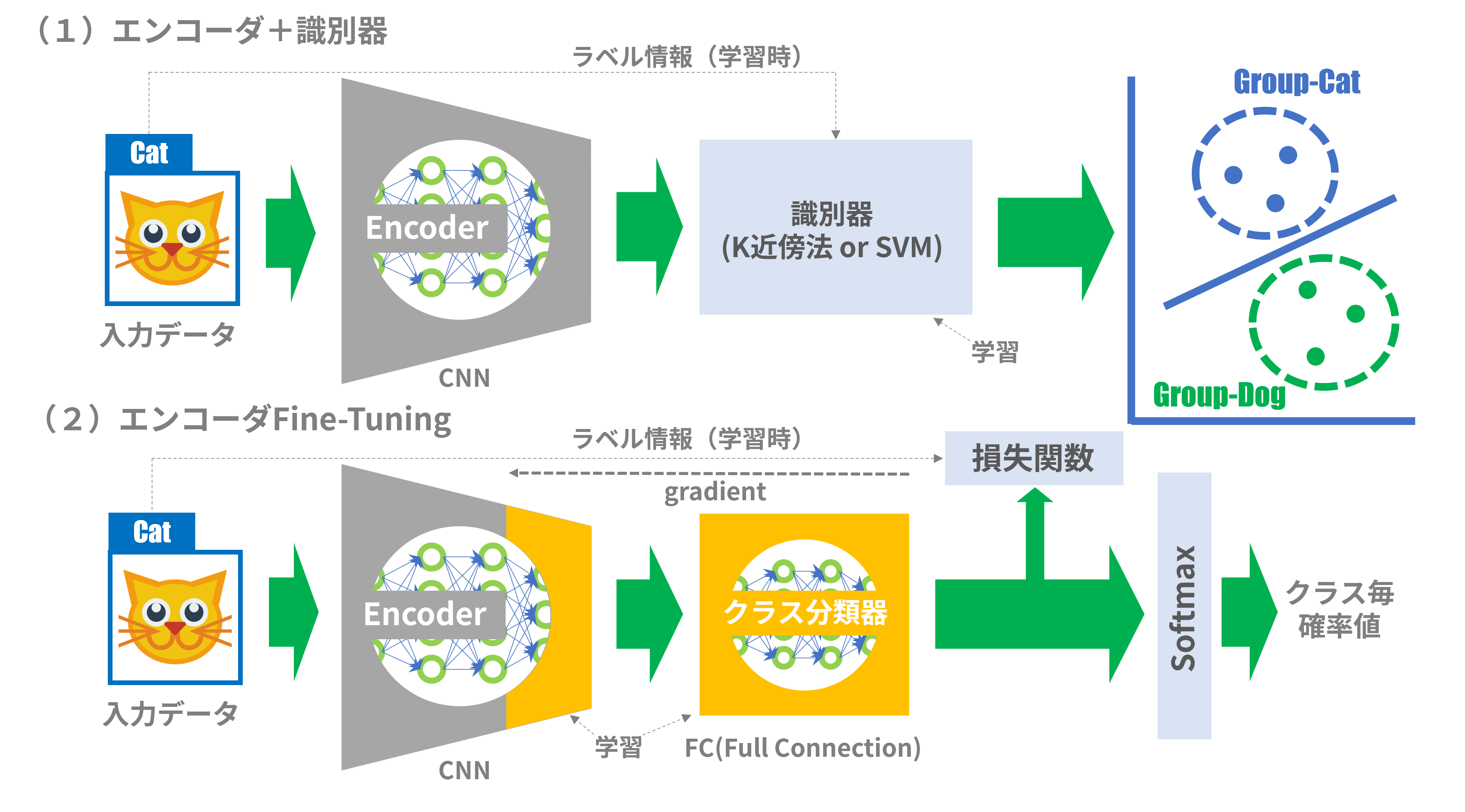
「Target Task」はこの学習済みエンコーダを用いて、さらに少量データによる教師あり学習(ラベルあり)を追加実施し、例えば未知画像のクラス判別などを実現します。Target Taskとして以下の手法があります(図3):
図3:Target Taskへの応用
図3の「Encoder」は図2の「Encoder:f」を取り出してTarget Taskのシステムに組み込んだものです。
(1)エンコーダ+識別器
以前の記事(Edge TPUで顔認証してみる)で紹介した方式そのものです。SSLで学習したエンコーダの重みパラメータを固定し(図3上の灰色部分はパラメータ固定を意味する)、特徴ベクトルの生成器として用います。さらに、エンコーダから出力された特徴ベクトルを入力とした「識別器」を次段に置きます。識別器としてはK近傍法やSVM等の機械学習でおなじみの手法を用います。最初に、実際のタスクに用いる入力画像データとラベル情報を少量用いて、識別器の教師あり学習を必要とします。
(2)エンコーダ Fine-Tuning
いわゆる転移学習などで用いられるFine-Tuningを実施します。図3下では、エンコーダの後段に全結合(Full Connection)のニューラルネットワークを置き、特徴ベクトルからクラス番号への変換を行います(=クラス分類器)。エンコーダは出力側のいくつかの層の重みパラメータのみを更新可能とし、それ以外の重みパラメータは固定します(灰色の部分)。最初に、実際のタスクに用いる入力画像データとラベル情報を少量用いて、エンコーダとクラス分類器の教師あり学習を必要とします。
6.まとめ
今回の記事では学習関係の用語がいろいろ登場して、その関係を調べるのに苦労しました。それにしても、SimSiamをはじめとした自己教師あり学習(Self-Supervised Learning)の隆盛には驚きです。こんな簡単な仕掛けで、教師あり学習をも凌駕する性能を達成できるとは、いったいどうなっているんだろうと思ってしまいます。
SimSiamの論文[1]では、SimSiamのアーキテクチャがEMアルゴリズム的な働きをすることによりうまく動作しているのではないかという仮説を立てています。後編では、この「仮説」について説明します。