ご覧いただきありがとうございます。
過去の記事も含め、全てのコードをGithubで公開しています。
前編では角度系深層距離学習の紹介と、その損失関数の基本となる「Sofmax Cross Entropy(SCE) Loss」(以下「SCE Loss」)について説明しました。後編では、それがなぜうまく働くのかについて説明したいと思います。この後編からお読みになった方は、式の定義等が前編で説明されているので、是非前編もご覧ください。
1.何が疑問だったか?
例えばFaceNetのようなユークリッド距離系距離学習では以下の2つの操作が行われます:
- 同じクラスに属する特徴ベクトルは近づける
- 異なるクラスに属する特徴ベクトルは遠ざける
一方、角度系距離学習では1番目の操作についてのみ留意し、2番目の操作は特に行われていないように見えます。
1番目の操作によって特徴ベクトルは所属するクラスの代表ベクトル周辺に固まります(これを便宜的にクラス毎の特徴ベクトル群と呼ぶ)。
仮に、2番目の操作が実施されれば異なるクラスの特徴ベクトル群は互いに離れた位置となるはずです。そしてこれは結果的に、クラス代表ベクトル同士が離れるということになります。
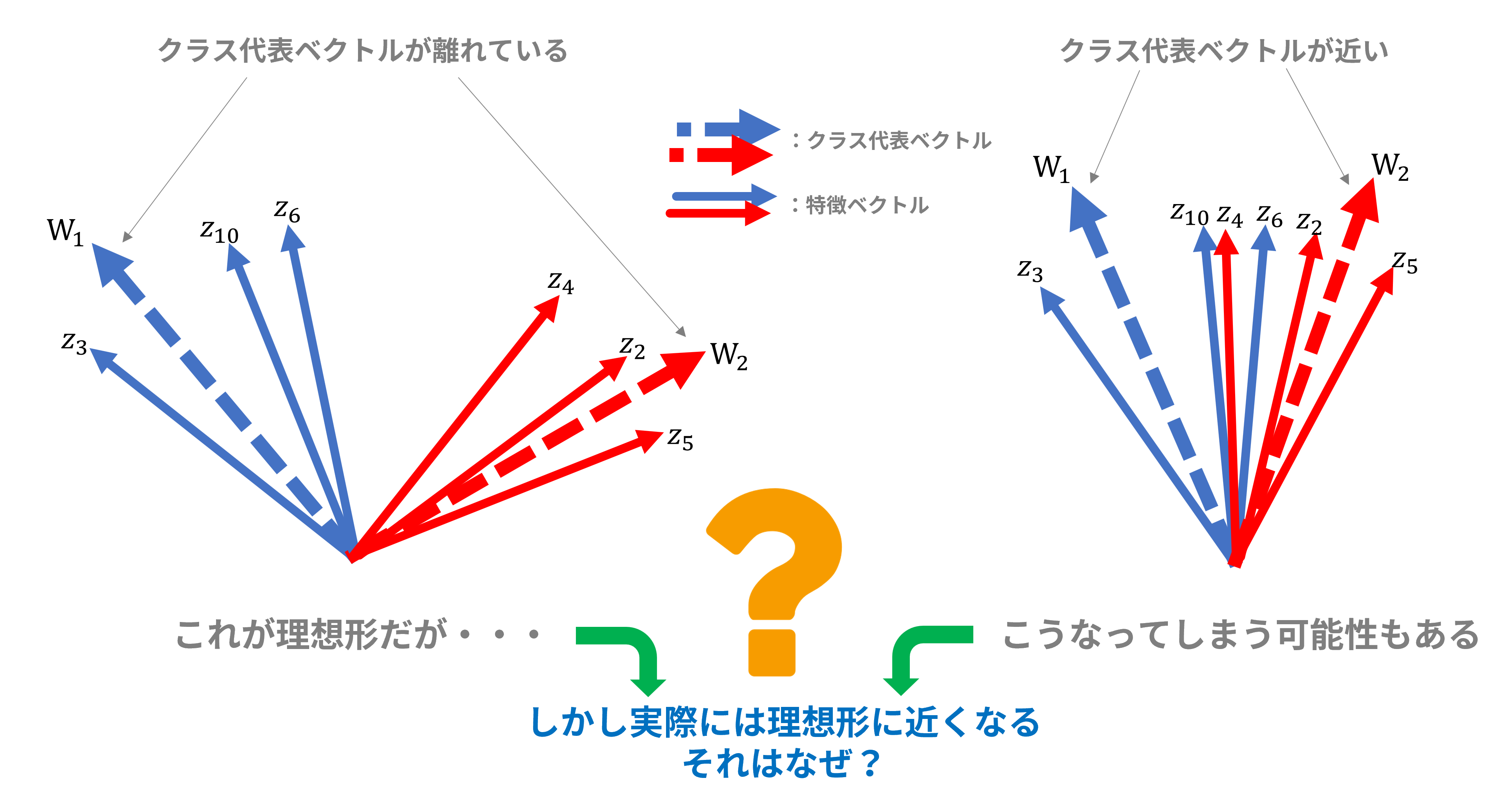
この2番目の操作が無ければクラス代表ベクトルどうしが近付いてしまい、特徴ベクトル群の分離が難しくなる可能性があります。図1の右側図ではそのような状況を表しており、例えばクラス1に属するはずの特徴ベクトル$z_6$はクラス2の代表ベクトル$W_2$に近く、クラス2に属するはずの特徴ベクトル$z_4$はクラス代表ベクトル$W_1$、$W_2$の中間にあり、どちらの特徴ベクトルも本来属するはずのクラス代表ベクトルに近いとは言えません。
図1:特徴ベクトル群とクラス代表ベクトルの位置関係
しかし実際にSCE Lossに基づく角度系距離学習では、図1の右側図のような状況になることはなく、図1の左側図のようにクラス代表ベクトルどうしが離れていることがほとんどです。
「2番目の操作を行っていないのに、なぜクラス代表ベクトルどうしが離れているのか?」、これについて以下に考察します。
2.さっそく種明かし
(1)式のおさらい
説明のため、前編に出てきた式を再掲します。
この式の意味するところは、推定された離散確率分布$q_i$が「1」に近付くほど交差エントロピー$H$が「0」に近付き、それは損失関数$\mathcal{L}_{Softmax}$が「0」に近付くことを意味します。
\begin{split}
\mathcal{L}_{Softmax}&=-\frac{1}{N}\sum\limits_{i=1}^NH(p_i, q_i)\\
H(p_i, q_i)&=-log(q_i(x=y_i))\\
q_i(x=y_i)&=\frac{e^{W_{y_i}^Tz_i}}{\sum_{j=1}^Le^{W_j^Tz_i}}\\
\end{split}
| 記号 | 定義 | 説明 |
|---|---|---|
| $\mathcal{L}_{Softmax}$ | Sofmax Cross Entropy Loss | |
| $N$ | バッチサイズ | 1バッチに含まれる入力データ数 |
| $H(p_i,q_i)$ | 交差エントロピー | 離散確率分布$p_i(x)$と$q_i(x)$の交差エントロピー |
| $x$ | 確率変数(の実現値) | ここではクラス番号を意味する。クラスが5つあれば1~5いずれかの整数となる |
| $p_i(x)$ | 真の離散確率分布 | 教師データ、つまり正解データの確率分布 |
| $q_i(x)$ | 推定した離散確率分布 | 学習データをニューラルネットワークに通した結果として得られた確率分布 |
| $L$ | 全クラス数 | |
| $z_i$ | 特徴ベクトル | 入力データをベクトル変換器に通して得られたベクトル(1次元テンソル) |
| $y_i$ | 所属クラス | 入力データが属するクラス。例えば$L=5$ならば1~5いずれかの整数となる |
| $W_k^T$ | クラス$k$の代表ベクトル | 各クラスの中心となる仮想的なベクトル。$T$は転置の意 |
(2)Softmax関数に注目してみる
ここで、$q_i(x=y_i)$を「1」に近付けるにはどうすればよいかについて考察します。
前編で「$q_i(x=y_i)$は0から1の値を取りますが、これが極力大きな値になるためには$e^{W_{y_i}^Tz_i}$が大きな値になればよさそうです」とざっくり書いてしまいましたが、実はここを深堀りすると答えが出てきそうです。
$q_i(x)$の動きを探るため、式を以下のように変形します:
\begin{split}
q_i(x=y_i)&=\frac{e^{W_{y_i}^Tz_i}}{\sum_{j=1}^Le^{W_j^Tz_i}}&=\frac{e^{W_{y_i}^Tz_i}}{e^{W_{y_i}^Tz_i}+\sum_{j\neq y_i}^{L-1}e^{W_j^Tz_i}}\\&=\frac{s}{s+C}
\end{split}
ここで、
s=e^{W_{y_i}^Tz_i}=e^{\|W_{y_i}\|\|z_i\|cos(\theta_{y_i})}\\
C=\sum_{j\neq y_i}^{L-1}e^{W_j^Tz_i}=\sum_{j\neq y_i}^{L-1}e^{\|W_j\|\|z_i\|cos(\theta_j)}
と、置きます。
$q_i(x)$式はSoftmax関数ですが、分母を$s$と$C$に分離するのがポイントです。
ここで$s$は特徴ベクトル$z_i$と、特徴ベクトル$z_i$が属するクラス$y_i$の代表ベクトル$W_{y_i}$との内積を$e$に乗じたものです。
また、$C$は特徴ベクトル$z_i$と、特徴ベクトル$z_i$が属するクラス$y_i$以外の代表ベクトル$W_{j\neq y_i}$との内積を$e$に乗じたものの総和です。
もうお気付きかもしれませんが、$C$は特徴ベクトル$z_i$とクラス$y_i$以外のクラス代表ベクトルとの内積で構成されているので、特徴ベクトルと異なるクラスの代表ベクトルとの角度と関係がありそうなことがわかります。
(3)q(x)の動きを探る
$q_i(x=y_i)$(以下、略して$q(x)$)を縦軸に、$s$を横軸にしたグラフが図2です。このグラフでは:
\|W_k\|= \|z_i\|=1\\
0\leqq\theta_{y_i}\leqq\pi\\
と仮定しています。この仮定の下で$s$は$1/e<s<e$の範囲であり、図2の網掛けしていない部分に相当します:
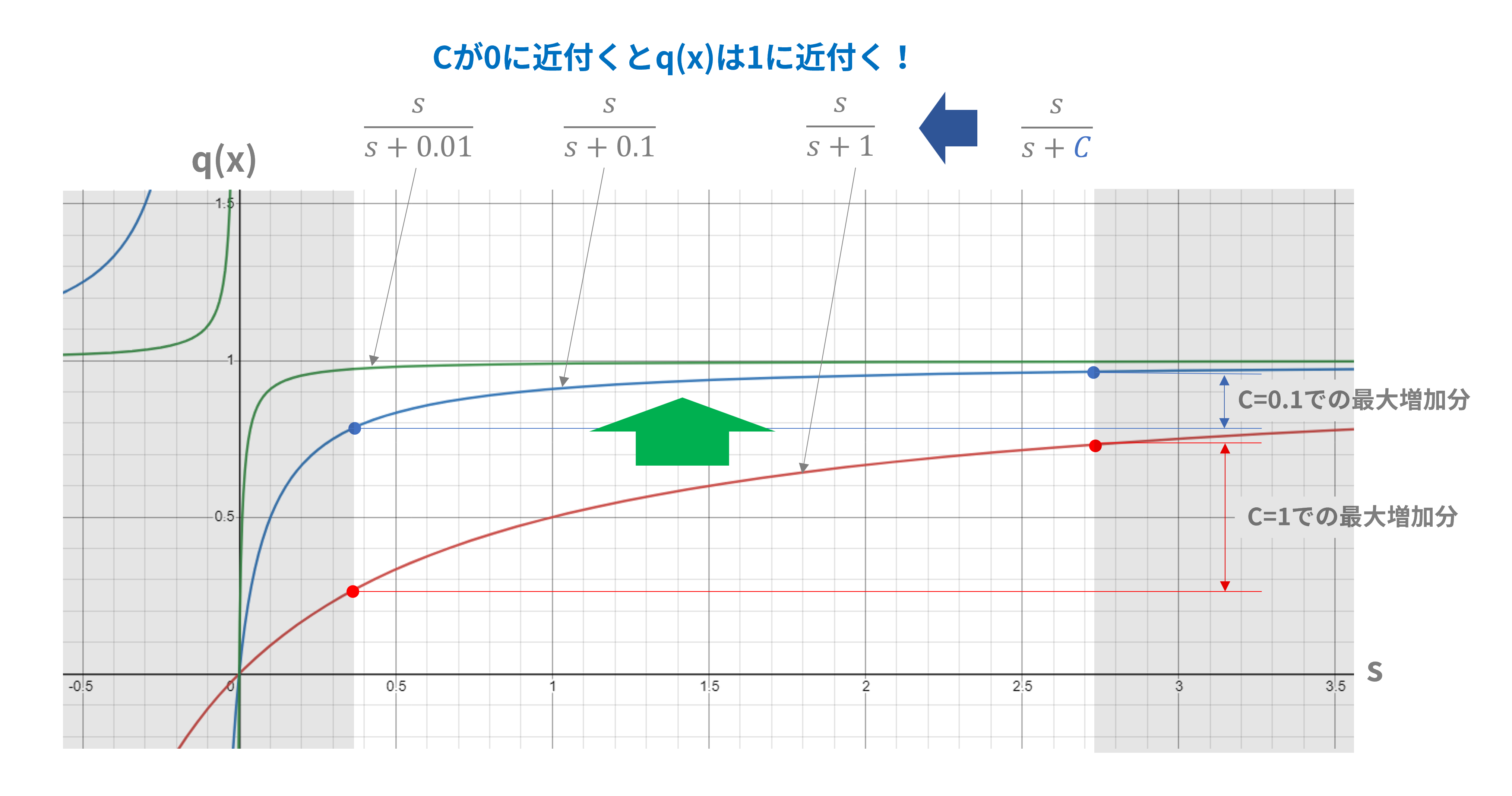
図2:q(x)とsの関係
図2から、$q(x)$と$s$との関係は双曲線となっていることがわかりますが、$s$は0より大きい値しかとらないので$s$が増加すれば$q_i(x=y_i)$も単調に増加する関係となっています。したがって、$s$が増加するほど$q(x)$は1に近付きます。「$q(x)$が極力大きな値になるためには$e^{W_{y_i}^Tz_i}$が大きな値になればよさそうです」というのは間違ってはいなさそうです。
一方で、$C$をパラメータとして0に近付けていくと、双曲線が漸近線:$q(x)=1$にどんどん近付いてきます。$C$が0に近付くほど曲線の傾斜が緩み、$s$が増加しても$q(x)$の増加に寄与しなくなってきます。例えば$C=0.1$と$C=1$において、$s$の増加による$q(x)$の最大増加分は前者の方が小さくなっています。
このグラフを見ると、なんだか$s$よりも$C$の方が$q(x)$に与える影響が大きそうに見えなくもありません。
(4)ではCとは何か?
では、$C$が小さくなるとはどういう意味があるでしょう?
$C$は特徴ベクトル$z_i$と、特徴ベクトル$z_i$が属するクラス$y_i$以外の代表ベクトル$W_{j\neq y_i}$との内積を$e$に乗じたものの総和です。
したがって、$C$の項「$e^{W_j^Tz_i}$(ただし$j\neq y_i$)」のすべてを0に近付けば$C$は0に近付きます。
$e^{W_j^Tz_i}$が0に近付くということは、特徴ベクトル$z_i$と特徴ベクトル$z_i$が属するクラス$y_i$以外の代表ベクトル$W_j$との内積が小さくなる=角度が大きくなることを意味します。特徴ベクトル$z_i$はクラス$y_i$の代表ベクトルのすぐ近くにあるので、結局、クラス$y_i$の代表ベクトルとクラス$y_i$以外の代表ベクトルとが離れるということになります。
以上をまとめますと:
- 損失関数$\mathcal{L}_{Softmax}$を0に近づけるには交差エントロピー$H$を0に近付ければよく、交差エントロピー$H$を0に近付けるには$q(x)$を1に近付ければよい
- $q(x)$を1に近付けるには$C$を0に近付けるのが効果的で、それはクラス代表ベクトル間が離れることを意味する
これが前出の疑問への回答となります。SCE Lossを小さくするためには特徴ベクトルとそのクラス代表ベクトルを近付けるだけではなく、クラス代表ベクトル間を離すようにも作用していたということです。
(5)ベクトル長の影響
上述の説明では「ベクトル長:$|W_k|= |z_i|=1$」と仮定していましたが、じつはこの仮定では$C$の最小値は「$(L-1)/e$」程度にしかなりません。例えばクラスが全部で5つしかないとすると($L=5$)、$C$の最小値は1.47程度という感じです。
しかし、ベクトル長を「$|W_k|= |z_i|=3$」と少し増やすだけで$s$も$C$も最小値はかなり0に近付き、最大値も格段に大きな値となります(図2の網掛けされていない部分が左右に拡がる)。
ベクトル長は$q(x)$の動きにかなり影響しそうなので、実験の際には注意が必要そうです。
| ベクトル長 | $s$の範囲(式) | $s$の範囲(数値例) | $C$の範囲(式) | $C$の範囲(数値例,L=5) |
|---|---|---|---|---|
| $1$ | $1/e<s<e$ | $0.36787<s<2.71829$ | $(L-1)/e<C<(L-1)e$ | $1.47151<C<10.8732$ |
| $3$ | $1/e^9<s<e^9$ | $0.00012<s<8103.09$ | $(L-1)/e^9<C<(L-1)e^9$ | $0.00049<C<32412.4$ |
(6)SCE Loss改良への動機
前の節で、図2において「$C$が0に近付くほど曲線の傾斜が緩み、$s$が増加しても$q(x)$の増加に寄与しなくなってきます」と書きました。
これは、学習の過程で$C$が0に近付いてくると$s$を増加させようと頑張る必要がなくなってくることを意味します。$s$の増加は特徴ベクトルとそれが属するクラス代表ベクトルとが近付くことなので、特徴ベクトル群はクラス代表ベクトルを中心に凝集することになります。
したがってある程度学習が進んで$C$が0に近付いてくると、特徴ベクトル群の凝集はどこかで止まっているがごとくになると予想されます。
特徴ベクトル群が凝集すると、特徴ベクトルのクラス分け精度は上がります(つまり、特徴ベクトル群が重ならない)。そこで、角度系距離学習の有名論文([1][2][3]等々)ではSCE Lossに独自のパラメータを導入し、特徴ベクトル群のさらなる凝集を競っています。
参考文献:
[1] SphereFace: Deep Hypersphere Embedding for Face Recognition.
[2] CosFace: Large Margin Cosine Loss for Deep Face Recognition.
[3] ArcFace: Additive Angular Margin Loss for Deep Face Recognition.
3.「N-Pair Loss」と「SCE Loss」との接点
FaceNetで用いられた「Triplet Loss」を改良したものの一つに「N-Pair Loss」というものがあります。じつは、これの式が「SCE Loss」の式にそっくりでしたという話です。
(1)まずTriplet Lossについて
Triplet Lossを計算するための学習サンプルとして、Anchor Vector(以下$z_a$)、Positive Vector(以下$z_p$)、Negative Vector(以下$z_n$)の三つ組み特徴ベクトル:${z_a,z_p,z_n}$を使います。$z_a$は距離を比較する基準となる特徴ベクトル、$z_p$は$z_a$と同じクラスに属する特徴ベクトル、$z_n$は$z_a$の属するクラスとは異なるクラスに属する特徴ベクトルです。
ここで、$z_a$と$z_p$の距離を$d_p$、$z_a$と$z_n$の距離を$d_n$と定義するとTriplet Lossの式は以下のようになります:
\mathcal{L}_{triplet}(\{z_a, z_p,z_n\})=max(0, d_p-d_n)
厳密には、学習を効果的に進めるために「マージン」というパラメータを取り入れるのですがここでは割愛します
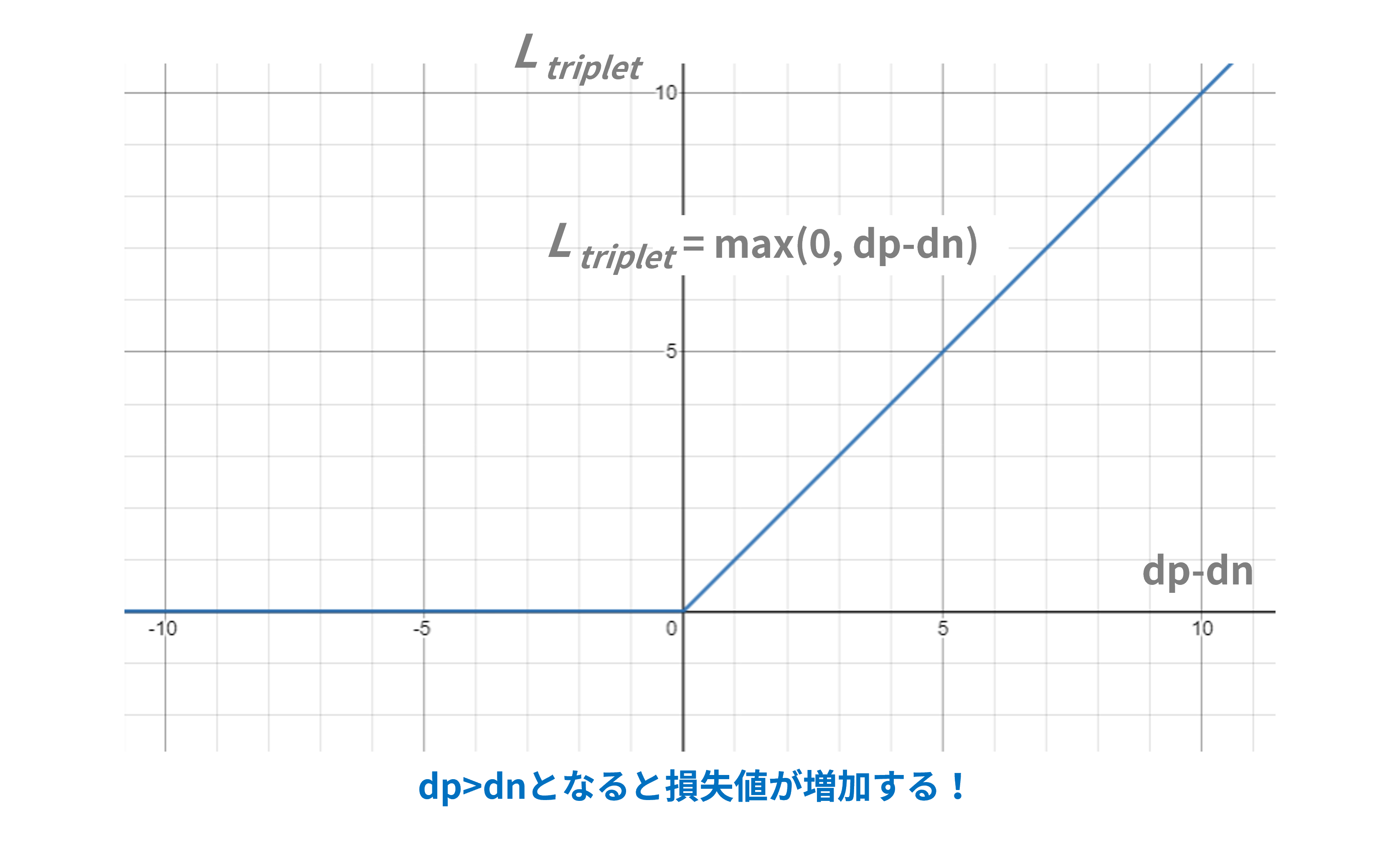
図3はTriplet Loss式をグラフ化したものです。$d_p>d_n(つまりd_p-d_n>0)$、すなわち同一クラス内のベクトル距離$d_p$が異クラス間のベクトル距離$d_n$よりも大きければ、その差分だけ損失値が大きくなります。損失値$\mathcal{L}_{triplet}$が大きくなれば学習によって損失が小さくなるようにニューラルネットパラメータが調整され、学習が進めば$d_p>d_n$の状態は解消されていきます。
図3:Triplet Lossの損失関数
(2)N-Pair Lossとは
Triplet Lossには学習に使われる三つ組み特徴ベクトル(特に$z_n$:Negative Vecor)を適切に選ぶのが難しく、計算コストもかかるという弱点がありました。
それならば、$z_n$を一つではなく複数個を一気に使って損失関数の計算を効率的に進めようというのがN-Pair Loss方式[4]です。
N-Pair Lossの式は以下のようになります:
\mathcal{L}_{(N+1)-tuplet}(\{z_a, z_p, \{z_{n_i}\}^{N-1}_{i=1}\})=log(1+\sum\limits_{i=1}^{N-1}e^{d_p-d_{n_i}})
ここで、
\{z_a, z_p, \{z_{n_i}\}^{N-1}_{i=1}\} = \{z_a, z_p, z_{n_1},...,z_{n_{N-1}}\}\\
d_p = d(z_a, z_p)\\
d_{n_i} = d(z_a, z_{n_i})\\
d(z_1,z_2)=特徴ベクトルz_1と特徴ベクトルz_2の距離
$N$は全部で$L$個あるクラスの中から$N$個のクラスの特徴ベクトルを選んで損失関数計算のためのサンプルデータとしたことを意味します(SCE Loss式の$N$とは無関係)。
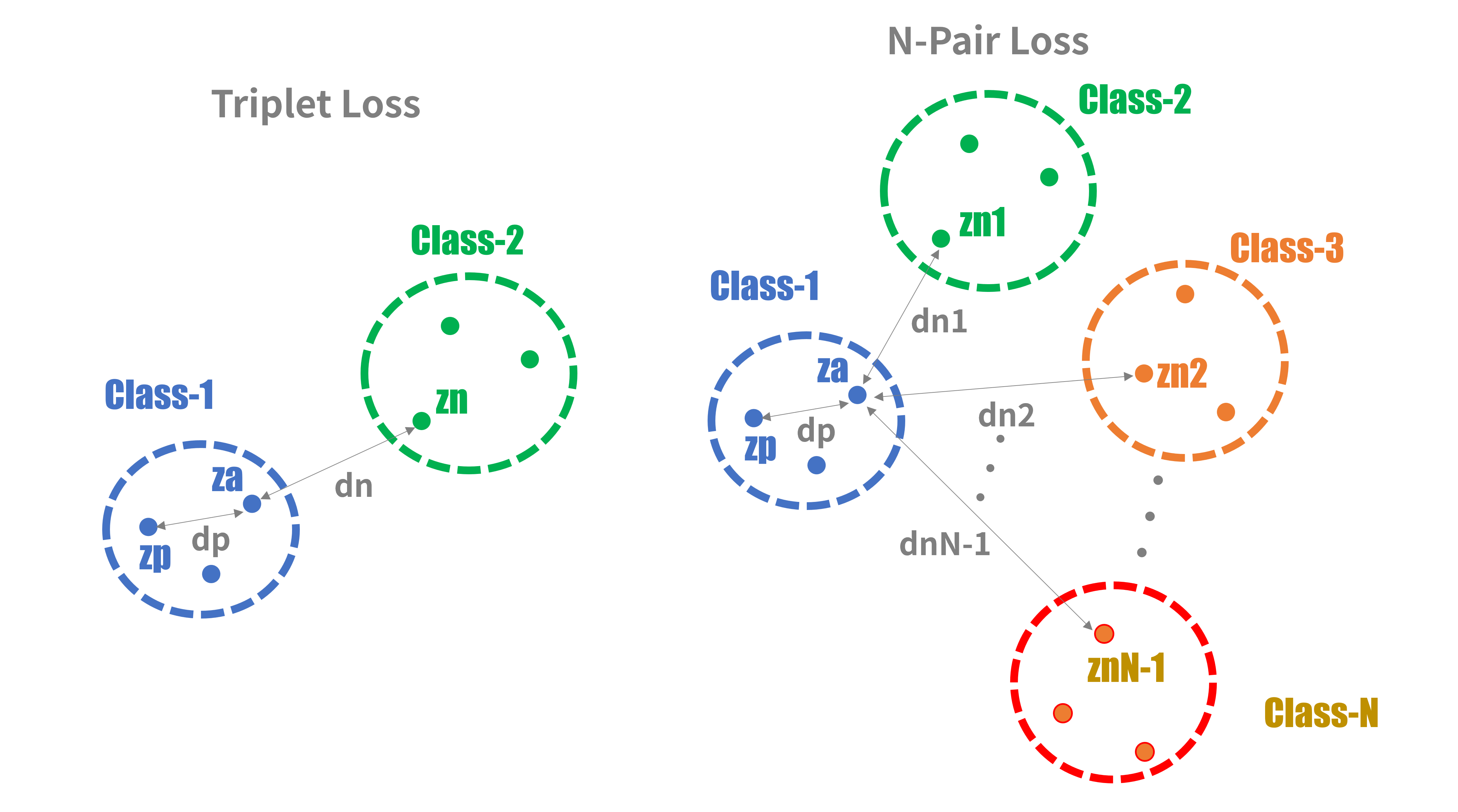
特徴ベクトル$s$、距離$d$とクラスの関係を図4に示します。
図4:特徴ベクトルの選び方比較
(3)N-Pair Lossの動き
上記でいきなり天下り的にN-Pair Loss式が出てきましたが、これがどんな動きをするのかを説明します。
式は典型的な「log-sum-exp」形式ですが、説明のため最初は$N=2$の場合をグラフ化してみます。
以下は$N=2$の場合のN-Pair Loss式です。$z_n$は1つしかないのでシグマは消えます:
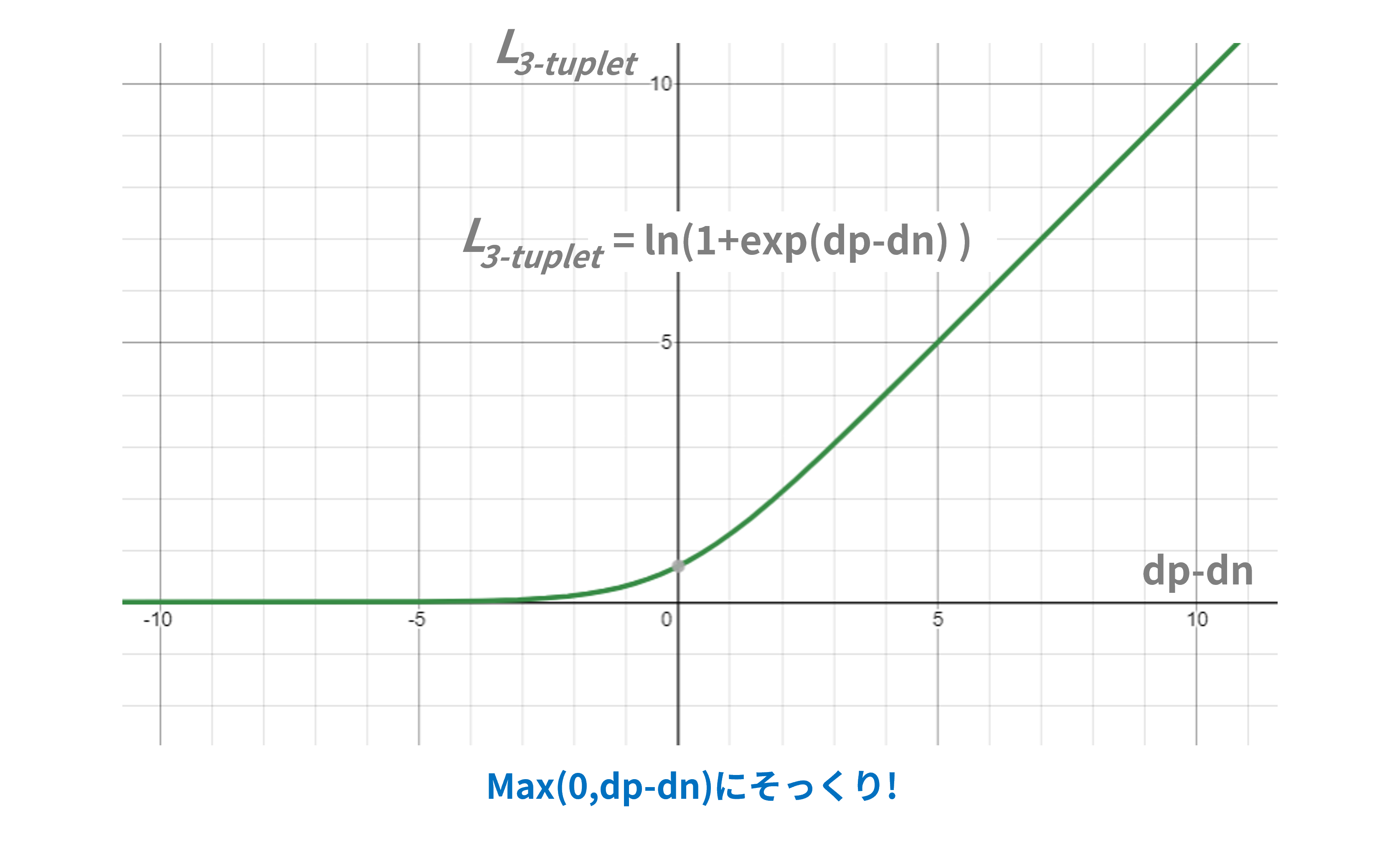
\mathcal{L}_{3-tuplet}(\{z_a, z_p,z_n\})=log(1+e^{d_p-d_n})
図5はN-Pair Loss式(ただし$N=2$)をグラフ化したものです。
どうでしょう、図3のTriplet-Loss式にそっくりですね。
$N=2$の場合はN-Pair LossはTriplet Lossと似たような挙動になりそうです。
図5:3-tuplet Lossの損失関数
では、$N$がもっと増えてシグマが入ってきたらどうなるか?
ここでまず、$d_{n_i}$を以下のように書き換えます:
d_{n_i} = d_{n\mu}+d_{n\delta_i}
$d_{n\mu}$は$d_n$の平均、$d_{n\delta_i}$は平均からの差分です。これを使ってN-Pair Loss式を変形すると:
\begin{split}
\mathcal{L}_{(N+1)-tuplet}(\{z_a, z_p, \{z_{n_i}\}^{N-1}_{i=1}\})&=log(1+\sum\limits_{i=1}^{N-1}e^{d_p-d_{n_i}})\\
&=log(1+\sum\limits_{i=1}^{N-1}e^{d_p-(d_{n\mu}+d_{{n\delta}_i})})\\
&=log(1+e^{d_p-d_{n\mu}}\sum\limits_{i=1}^{N-1}e^{-d_{{n\delta}_i}})\\
&=log(1+e^{d_p-d_{n\mu}+m})
\end{split}
ここで、
m=log(\sum\limits_{i=1}^{N-1}e^{-d_{{n\delta}_i}})
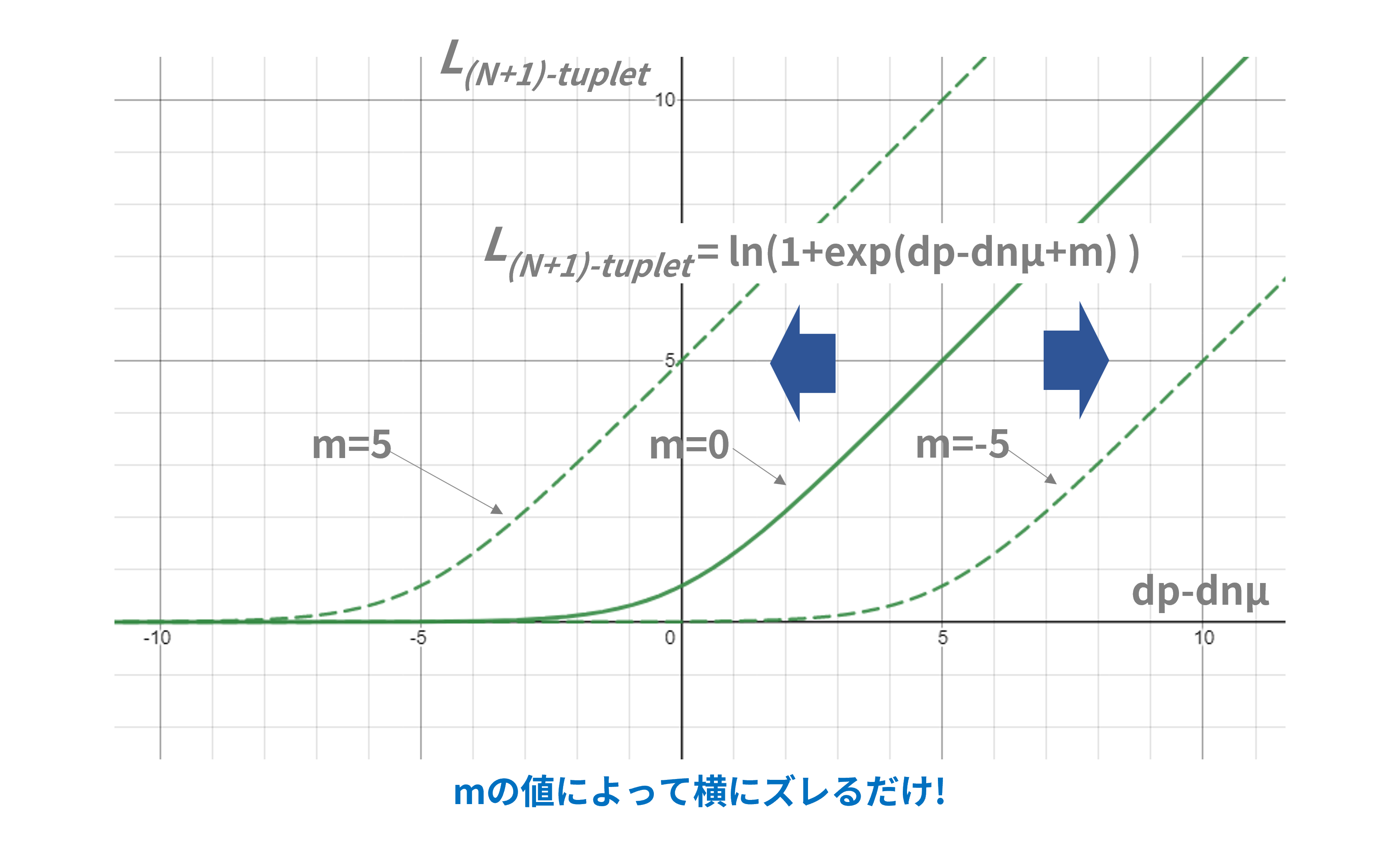
です。上式をグラフ化したのが図6です。基本的には3-tuplet Loss式のグラフ(図5)をパラメータ$m$だけ左右にずらすという感じですね。
パラメータ$m$がどれくらい動くのかが考察できていないのではっきりしたことは言えないのですが、グラフの形からは「同一クラス内のベクトル距離$d_p+m$が異クラス間のベクトル距離$d_n$よりも大きければ、その差分だけ損失値が大きくなる」という性質は維持していると思われます。
図6:(N+1)-tuplet Lossの損失関数
(4)SCE Lossとの類似性
じつは式が似ている話と上記のグラフの話はあまり関係ないのですが、まあ、N-Pair Loss式にはこういう性質がありますってことで載せてみました。softmax関数が実はmax関数の代用になるとは知らなかった。
ここまで、同一クラス内のベクトル距離を$d_p$、異クラス間のベクトル距離を$d_n$としてきましたが、そのベクトル距離がユークリッド距離なのか角度なのかは曖昧にしていました。
そこでベクトル距離を以下のように角度で定義してみます:
d_p = z_p^Tz_a
=\|z_p\|\|z_a\|cos(\theta_p)\\
d_{n_i} = z_{n_i}^Tz_a
=\|z_{n_i}\|\|z_a\|cos(\theta_{n_i})\\
角度(=距離)が小さく/大きくなるほど内積は大きく/小さくなるので、今までの「$d_p - d_{n_i}$」は「$d_{n_i} - d_p$」で表されます。
したがって、N-Pair Loss式は以下のようになります:
\begin{split}
\mathcal{L}_{(N+1)-tuplet}(\{z_a, z_p, \{z_{n_i}\}^{N-1}_{i=1}\})&=log(1+\sum\limits_{i=1}^{N-1}e^{d_{n_i}- d_p})\\
&=log(1+\sum\limits_{i=1}^{N-1}e^{z_{n_i}^Tz_a - z_p^Tz_a})\\
&=log(1+e^{-z_p^Tz_a}\sum\limits_{i=1}^{N-1}e^{z_{n_i}^Tz_a})\\
&=-log(\frac{1}{1+e^{-z_p^Tz_a}\sum_{i=1}^{N-1}e^{z_{n_i}^Tz_a}})\\
&=-log(\frac{e^{z_p^Tz_a}}{e^{z_p^Tz_a}+\sum_{i=1}^{N-1}e^{z_{n_i}^Tz_a}})\\
\end{split}
ここで、この式の変数を以下のSCE Loss式の変数に置き換えてみます:
N \Rightarrow L\\
\{z_a, z_p, \{z_{n_i}\}^{N-1}_{i=1}\} \Rightarrow \{z_i, W_{y_i}, \{W_j\}^{L-1}_{j\neq y_i}\}
するとSCE Loss式の中の$H(p_i, q_i)$:
H(p_i, q_i)=-log(q_i(x=y_i)) = -log(\frac{e^{W_{y_i}^Tz_i}}{e^{W_{y_i}^Tz_i}+\sum_{j\neq y_i}^{L-1}e^{W_j^Tz_i}}) = -log(\frac{e^{W_{y_i}^Tz_i}}{\sum_{j=1}^Le^{W_j^Tz_i}})
と同じになります。
N-Pair Lossでは、サンプル特徴ベクトルのPositive VectorやNegative Vectorとして各クラスから実在する特徴ベクトルを選んでいましたが、SCE Lossでは仮想的なクラス代表ベクトルを用いているのが大きな違いです。しかし、まったく違う発想から似たような損失関数式が導かれるのは面白いと思いました。
参考文献:
[4] Improved Deep Metric Learning with Multi-class N-pair Loss Objective
4.まとめ
今回は式をいろいろいじってグラフの動きを探ってみました。
数学的というよりは感覚的な考察でしたが、Softmax関数がこんなに奥が深いものとは意外でした。
単に確率化するための辻褄合わせ関数ではなかったのですね。
まあ、SCE Lossによる角度系距離学習がそこそこうまくいく理由はなんとなくわかりました。
しかし、残された疑問も少しあります:
-
本記事では特徴ベクトルやクラス代表ベクトルの長さが一定と仮定したが、本当に必要な仮定なのか?また、ベクトル長正規化のしくみを組み込むことで学習(Back propagation)にどのような影響が出るか?
-
未学習のクラスデータをクラス分け(オープンセット分類)できるか?FaceNetではビシッとできていました。SCE Loss(というかSoftmax関数)に基づく角度系距離学習では、学習済みのクラスしか分類できないようなイメージがあります。
特に2番目の疑問は実用面では重要で、大量のセレブ顔画像で角度系距離学習しても自分たち一般人の顔は判別できず、一から学習が必要となれば使いものになりません。
その辺りのことは意外にどこにも話題にされていないので、判ったらネタにしたいと思います。