機械学習初心者でも、サポートベクターマシン(SVM)のマージン最大化について理解しなければならない日がいつか来る。なので初心者代表の私が、SVMマージン最大化について初心者なりに分かりにくいところなどを含め解釈したものをまとめてみました。
加筆修正のコメント等あれば、遠慮なく教えてください。
1. なぜ人はSVMマージン最大化を学ぶのか
それはズバリ、機械学習を勉強している人には必須とも言えるサポートベクターマシン(SVM)の基本原理となっているからです。SVMの理解のためには、SVMマージン最大化の深い理解が必要不可欠です。
SVMはこのマージン最大化において、ハードマージンという概念を基にしたソフトマージンというものを採用しています。なので今回は、まず基盤となっているハードマージンについて説明した後にソフトマージンの説明をしようと思います。
実はSVMにはL1-SVMとL2-SVMがあるのですが、今回はL1-SVMに限定して説明を行います。(違いについてはこちら→SVMにおける損失と正則化)
2. ハードマージン最大化
ハードマージン最大化については、初心者の初心者による初心者のためのSVMハードマージン最大化にて説明しています。
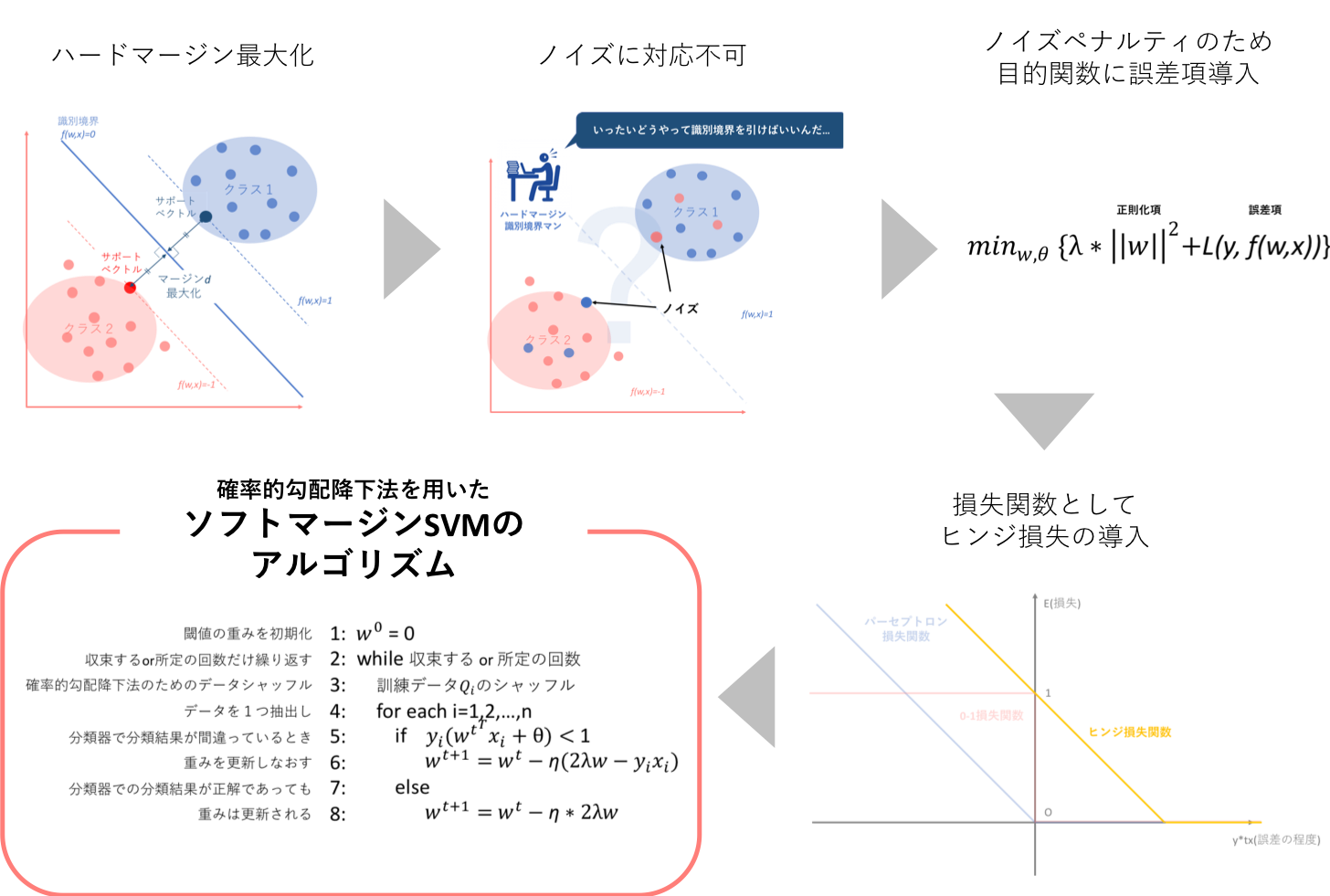
しかし、このように単純パーセプトロンの汎化性能(汎化能力 : generalization ability)の低さを補うためのハードマージン最大化という条件ですが、このハードマージンにも未だ弱点があります。それは、SVMでの2クラス線形分離において『データに誤分類されたノイズが混在している場合、線形識別境界を引くことができない』ということです。これはハードマージン最大化での数理計画問題における制約条件によるものです。
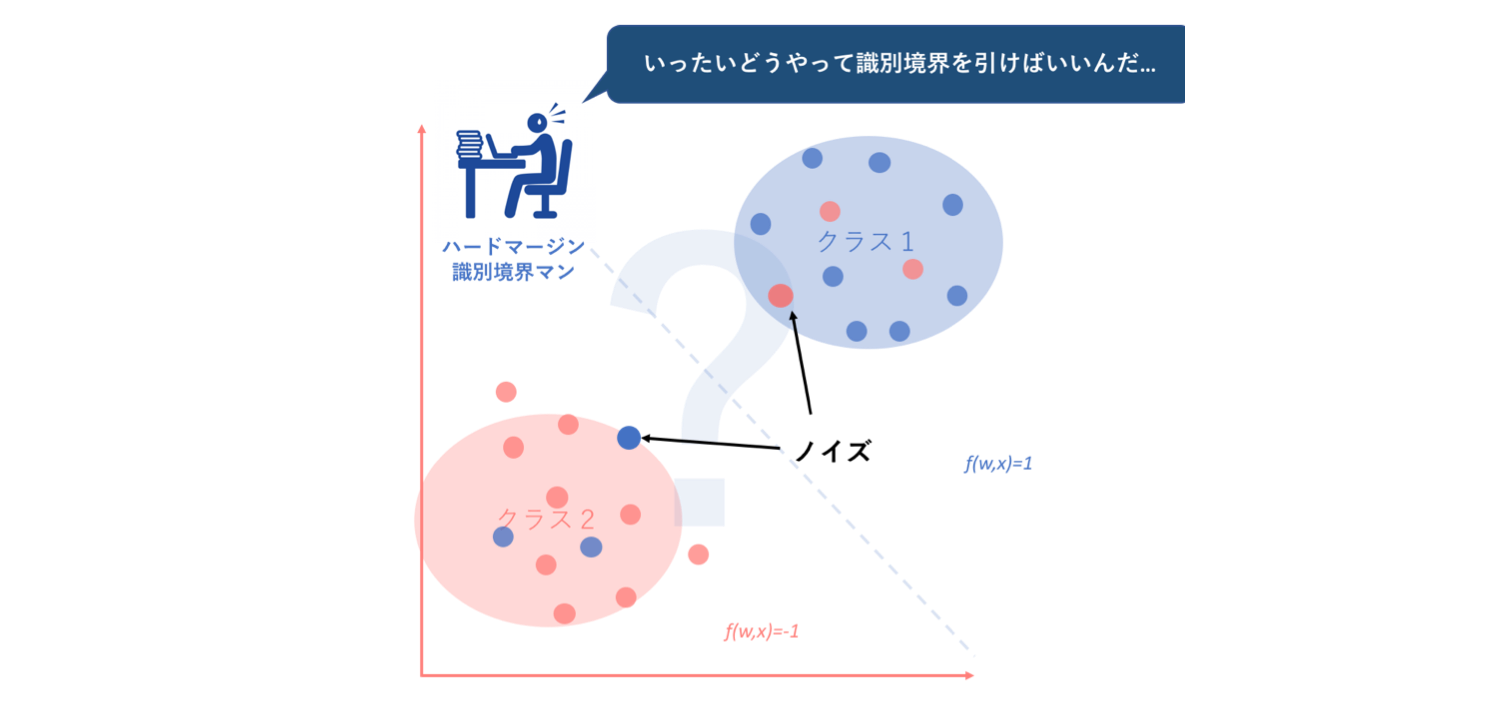
しかし現実問題において、ノイズが入らないような教師データの収集は非常に困難であり、それはつまりハードマージン最大化の実用性の乏しさを示しています。
そこでこのようなハードマージン最大化の抱える弱点を克服するために新たに考えられたのが、ソフトマージン最大化という考え方です。
3. ソフトマージン最大化
ソフトマージン最大化という概念は、基盤は以下の3つによって成り立っています。
①ハードマージン最大化の弱点克服
②ヒンジ損失(hinge loss)の導入
③勾配法アルゴリズムベース
それでは、これら3つを上から順にみていくことによってソフトマージン最大化への理解を深めていきます。
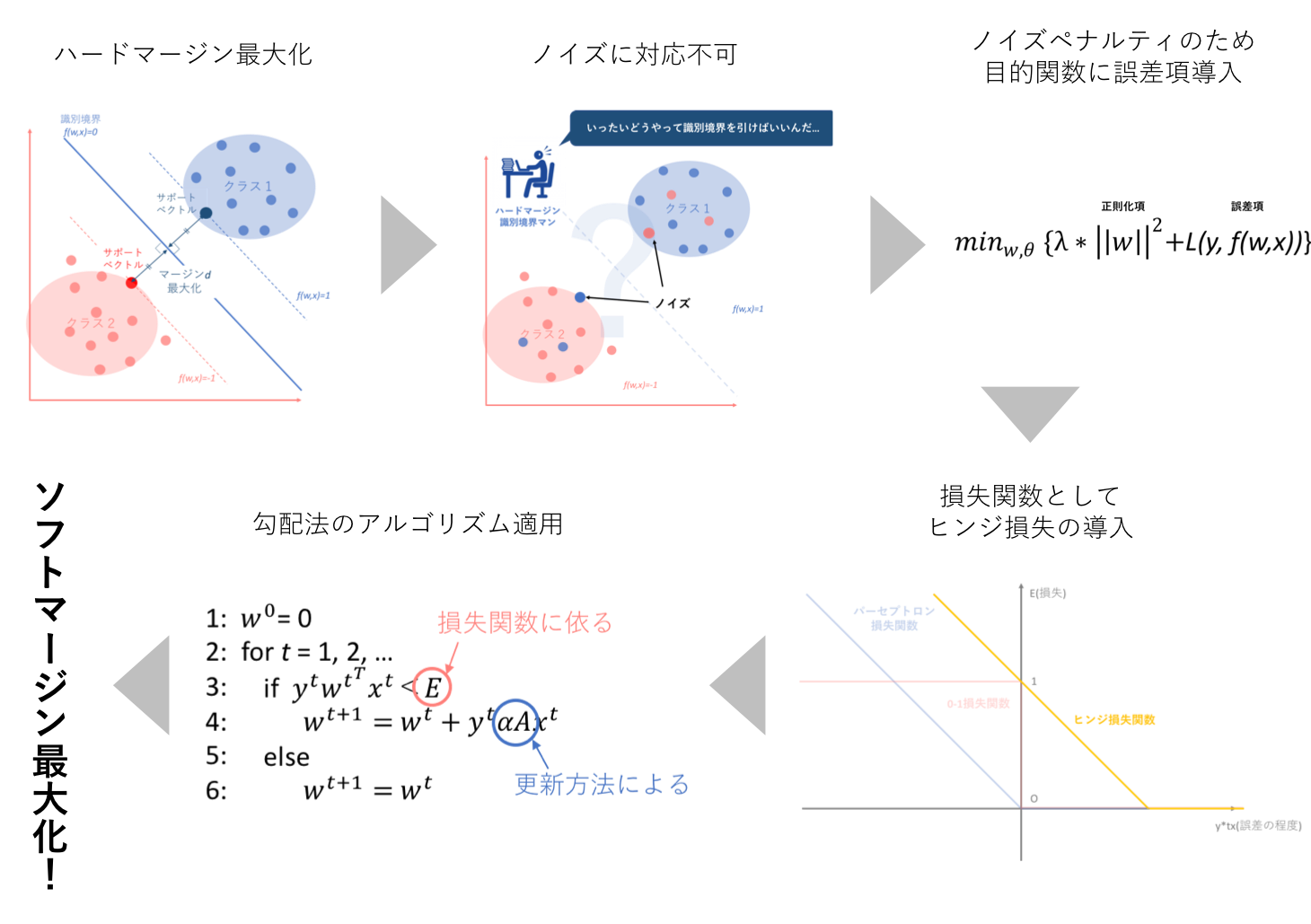
以下の図は、そのフローをまとめたものです。
🔥初心者ゾーン突入🔥
ひょっとすると、単純パーセプトロンが土台だと言っているにも関わらず、このソフトマージンの構成フロー内で単純パーセプトロンについて何も述べられていないじゃないかと思われる方がいるかもしれません。僕もそう思いました。
しかしパーセプトロンという言葉の定義を初心者の初心者による初心者のための単純パーセプトロンで確認すれば、入力に基づいて出力をステップ関数によって求めるのが単純パーセプトロンでした。よって、上記のフローには含めていませんが、単純パーセプトロンはSVMにおいてその仕組み自体が大前提となっていることが伺えます。
🔥初心者ゾーン脱出🔥
3.1. ハードマージン最大化の弱点克服(リターンズ)
ハードマージン最大化の弱点として、ノイズに対応できないというものがあるというのは上述しました。では、どのようにしてこの弱点を克服すれば良いのでしょうか。
3.1.1. ソフトマージンSVMの定式化
**ソフトマージンでは、この弱点をハードマージンの目的関数に損失関数加えることによって解決しようとします。**つまり、「教師データに誤分類が混在していることは一旦目をつむるが、その代わりにペナルティを与える!」と制約条件を緩め、目的関数にペナルティを追加します。
上図のように、**ソフトマージンではハードの目的関数に加えて誤差項としての損失関数を導入し、この導入に応じて制約条件を追記します。また、λ > 0は損失関数を用いて表されるペナルティとハードマージン最大化関数の間のトレードオフを制御するパラメータです。**λ→∞のときハードマージンSVMとなります。
ソフトマージンSVMについては、損失関数を加えるだけなのでそれほど難しくはないと思います。しかし損失関数の導入によって、数理計画問題の制約条件が変化します。これについては理論的説明のみにとどめますが
・誤分類の場合のずれを数値化するために損失関数L(y,f(w,x))を導入したので、ハード数理問題の制約式がその分だけ緩くなる
・誤分類がないことが前提となるので、損失が負になる(つまり正分類に対し利得を設ける)ことはなく、損失関数は常に0以上
が更新された制約条件となります。
3.3.2. ソフトマージンSVMの目的関数の概観
ここで、ソフトマージン最大化における数理計画問題の定式化ができたので、もう一度目的関数を概観してみましょう。

ソフト目的関数にて、左項は正則化項、右項は誤差項と呼ばれます。この呼び方の違いはおそらくあまり重要ではないと思うのですが、少し突っ込んでみましょう。右項は損失関数なので、誤差項と呼ばれるのは受け入れやすいと思います。しかし左項のハードマージン最大化関数は、なぜ正則化項と呼ばれるのでしょうか。
正則化(regularization)について詳しい説明は別の記事で紹介しようと思いますが、正則化とは簡単に述べると、機械学習で過学習を防ぎ汎化性能を高めたり、逆問題での不良設定問題を解くために追加の項を導入する手法(wiki参照)です。今回の場合において、ハード関数に追加項として損失関数を追加した目的はあくまで教師データの現実性に対応するためなので、追加された損失関数は正則化項とは言えません。しかし一方でハード関数||w||^2は、単純パーセプトロンの汎化性能を高めるために導入されたマージン最大化という条件を示しているので、その点で正則化していると言えます。この理由から、左項は正則化項、右項は誤差項と呼ばれるのではないでしょうか。
この点非常に細かいところなのですが、気になるところであったので記しておきました。
🔥初心者ゾーン突入🔥
また、余談なのですが、制約条件は略号でs.t.と表されます。これを私はsuch that の略称なのだと思っていましたが、経済学の授業でsubject toの略として使用されていました。一体どちらが正解なのでしょう。
Yahoo!知恵袋によれば、「普通は(一般の数学、全般では) such thatが多い。が拘束条件のもとでも最適化 最小化 最大化などを求めるときはsubject to が多い。したがって 経済学の本をみているならsubject to の略とするのが主流となる。置き換えて自然な方をとればいい。当然どっちでもかわらないならどっちでもいいどちらでも言いたい本質は変わらない」とされていました。ほんとにどっちでもいいんですね(笑)
ただ、s.t.が何の略称か知っておくのは必要なことなので、気に留めておくといいと思います。
ソース: such that と subject to は同じ意味でしょうか。
🔥初心者ゾーン脱出🔥
3.1.3. 本項まとめ
以上の議論をまとめます。
ソフトマージンSVMは以下のように定式化され、

①正則化項:正分類されたデータについてはハードマージンを最大化
②誤差項 :誤分類されたデータについてはペナルティ(合計or抽出されたもののみ)の最小化
という2つの目的関数の和であり、どちらを重要視するかがλという定数によって決められることになります。誤差項の部分の合計or抽出されたもののみについては、この数理計画問題の解き方によって異なります。
3.2. ヒンジ損失(hinge loss)の導入
ハードマージンSVMに損失関数を導入することによってソフトマージンSVMとすることは上述しました。では具体的に、ソフトマージンにはどのような損失関数を導入すれば良いのでしょうか。
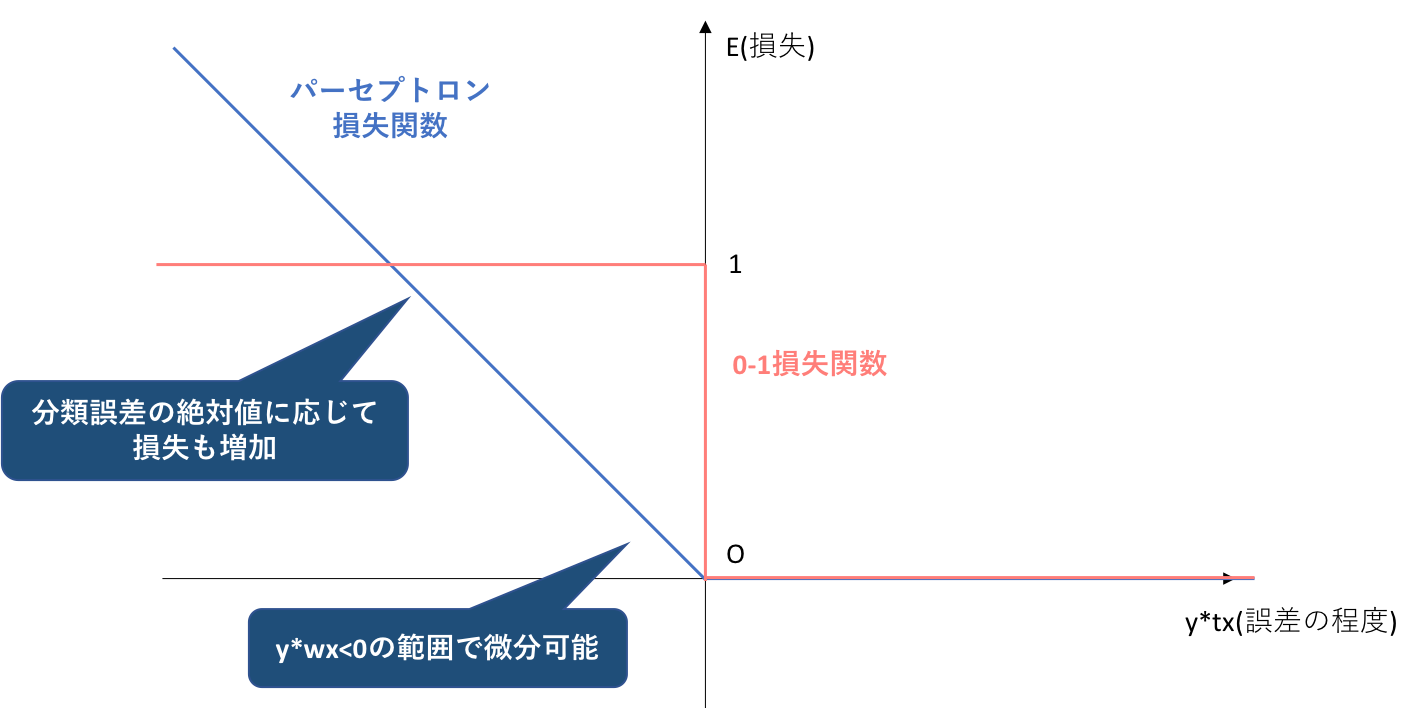
3.2.1. 0-1損失関数とパーセプトロン損失関数
一般的に損失関数において基盤となっているのは0-1損失関数ですが、0-1損失関数には
分類がギリギリ成功するケースと余裕を持って成功するケース、あるいは同様に分類がギリギリ失敗するケースと完全に間違っているケースを区別できない
・勾配法と呼ばれる手法を重み値を求める際に用いたとき、損失関数の微分が必要になるが、0-1損失関数は微分値が常に0になるという状態であり、勾配法に適さない
という2つの弱点がありました。そしてこの弱点を克服するべく設けられた代理損失関数が、パーセプトロン損失関数でした。(→初心者の初心者による初心者のための単純パーセプトロン)
3.2.2. パーセプトロン損失関数では不十分なワケ
では、ソフトマージンSVMにおいてもパーセプトロン損失関数を導入するのが望ましいのでしょうか。結論から言うと、No!です。ソフトマージンSVMにおいては、ヒンジ損失関数というパーセプトロン損失関数を平行移動させたものを用います。
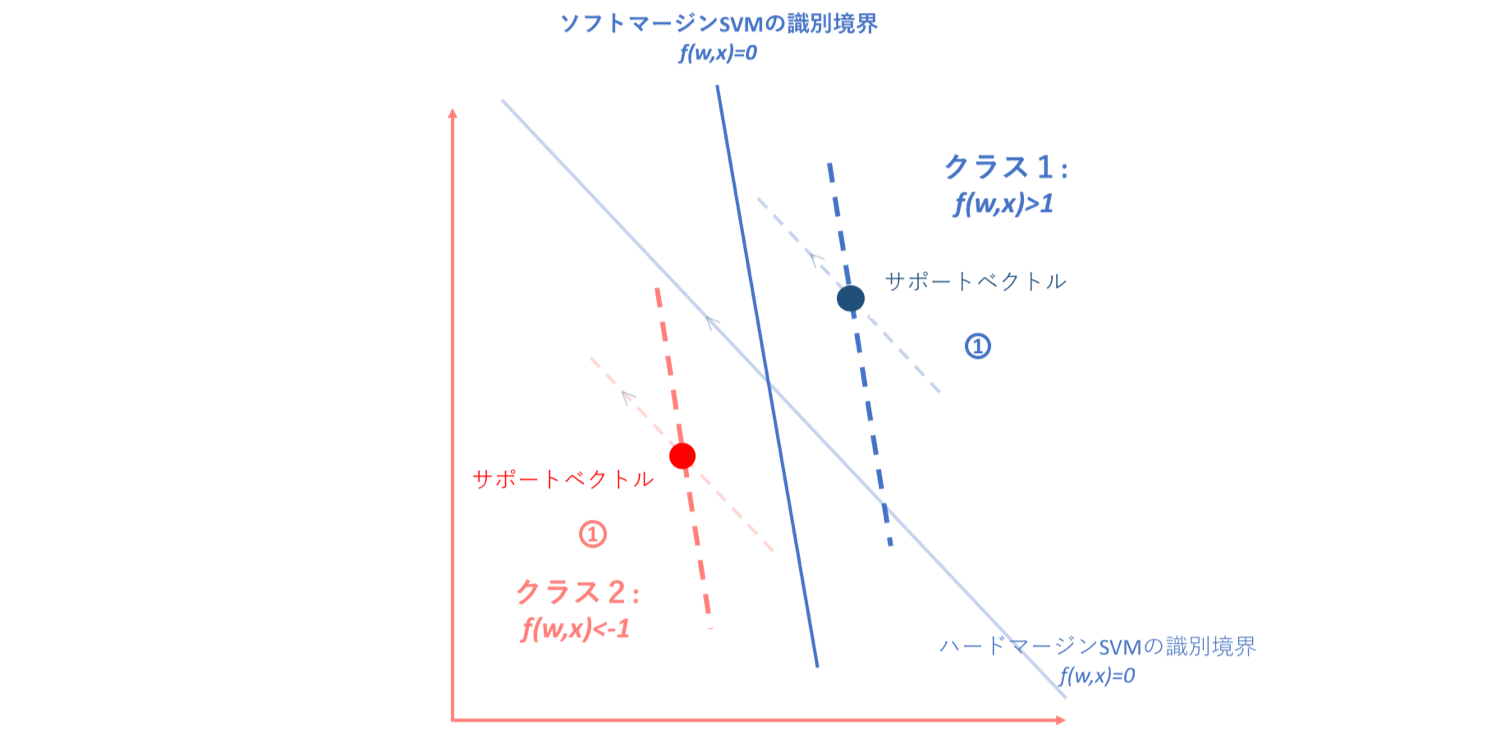
理由説明のファーストステップとして、ハードマージンSVMを図式化したものをもう一度見てみましょう。
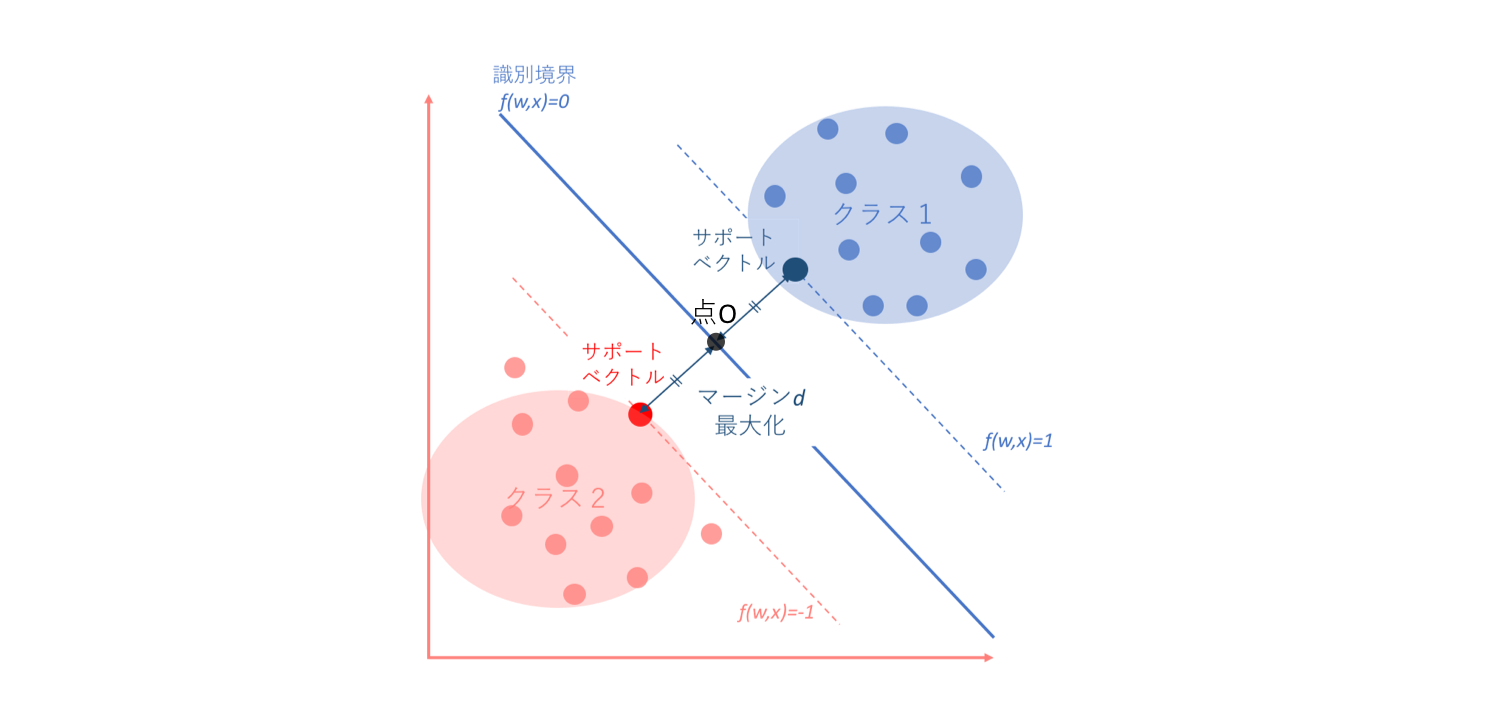
初心者の初心者による初心者のためのSVMハードマージン最大化にて、なぜクラス1がf(w,x)>1, クラス2がf(w,x)<-1になるかという話はしました。ハードマージンSVMにおいては、上の図からもわかるように-1<f(w,x)<1にはいずれの点も存在しないことが前提となっています。
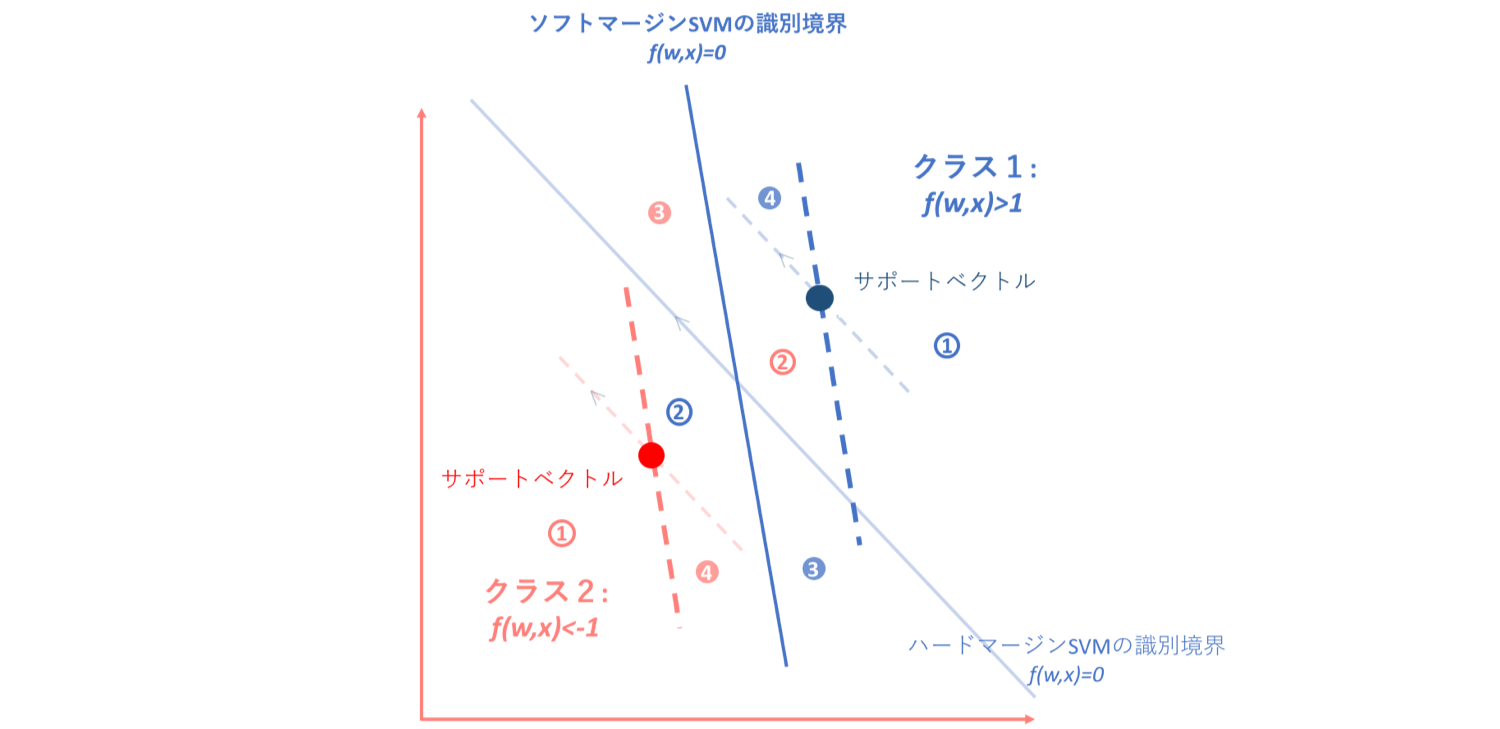
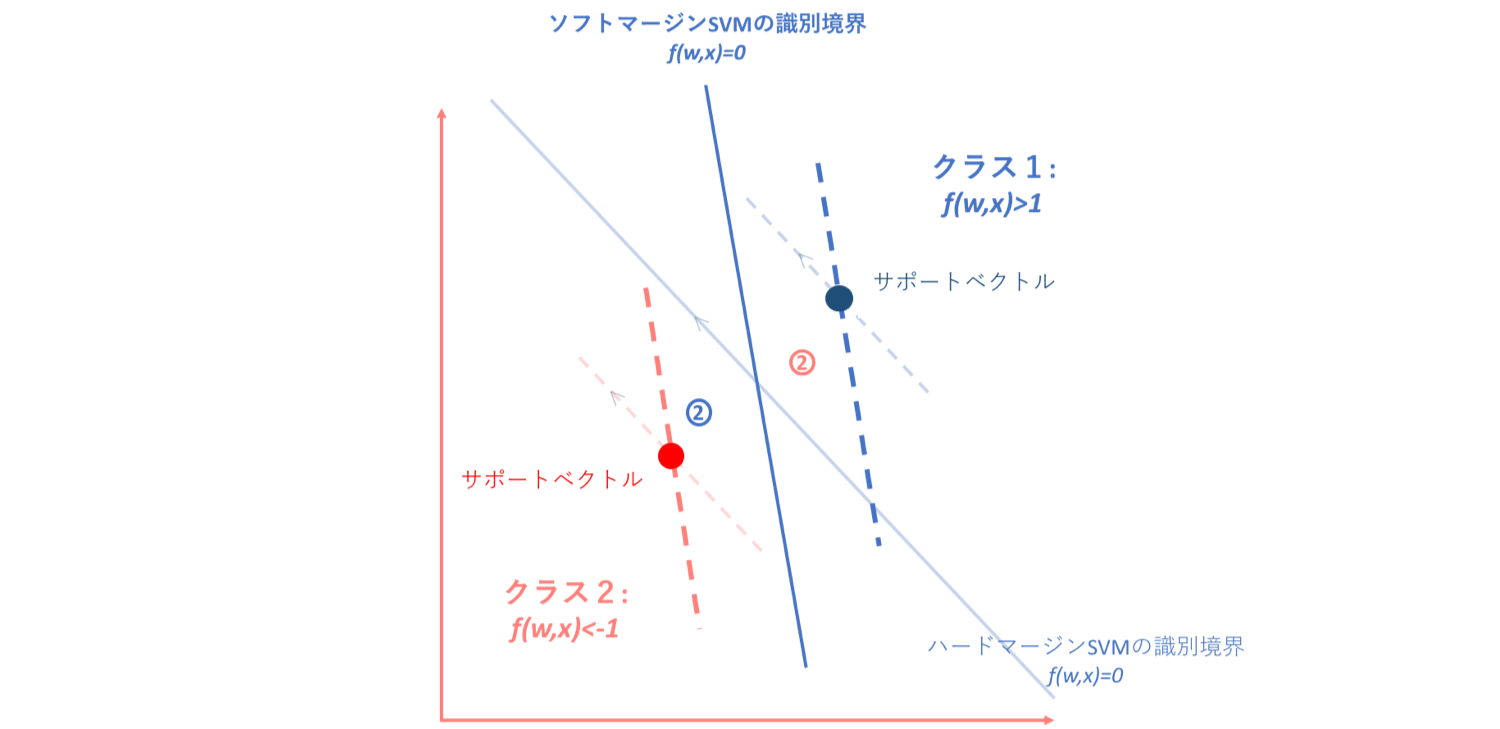
しかしソフトマージンSVMにおいては、制約条件の緩和によりこの前提が崩れます。そして、仮にソフトマージンSVMが引けるとわかっていた場合、以下の図のようにデータは4つのグループに分かれます。
ではそれぞれ細かく見ていきましょう。
①ハード/ソフトSVMいずれの場合もf(w,x)≧1 or f(w,x)≦-1に位置する点
このゾーンについてはハード/ソフトSVMどちらにおいても正分類されているものなので、特にペナルティであったり識別境界に影響を与えることはありません。
②ハード/ソフトSVMいずれの場合においても誤分類されているデータ
このゾーンでは、ハード/ソフトいずれの場合も直線形の識別境界を引こうとすれば誤分類されることになってしまいます。よってそれに対するペナルティを与えなければならないのですが、このゾーンはそもそも誤分類されてしまっているデータ集合なので、パーセプトロン損失関数の導入によってペナルティを与えることができます。
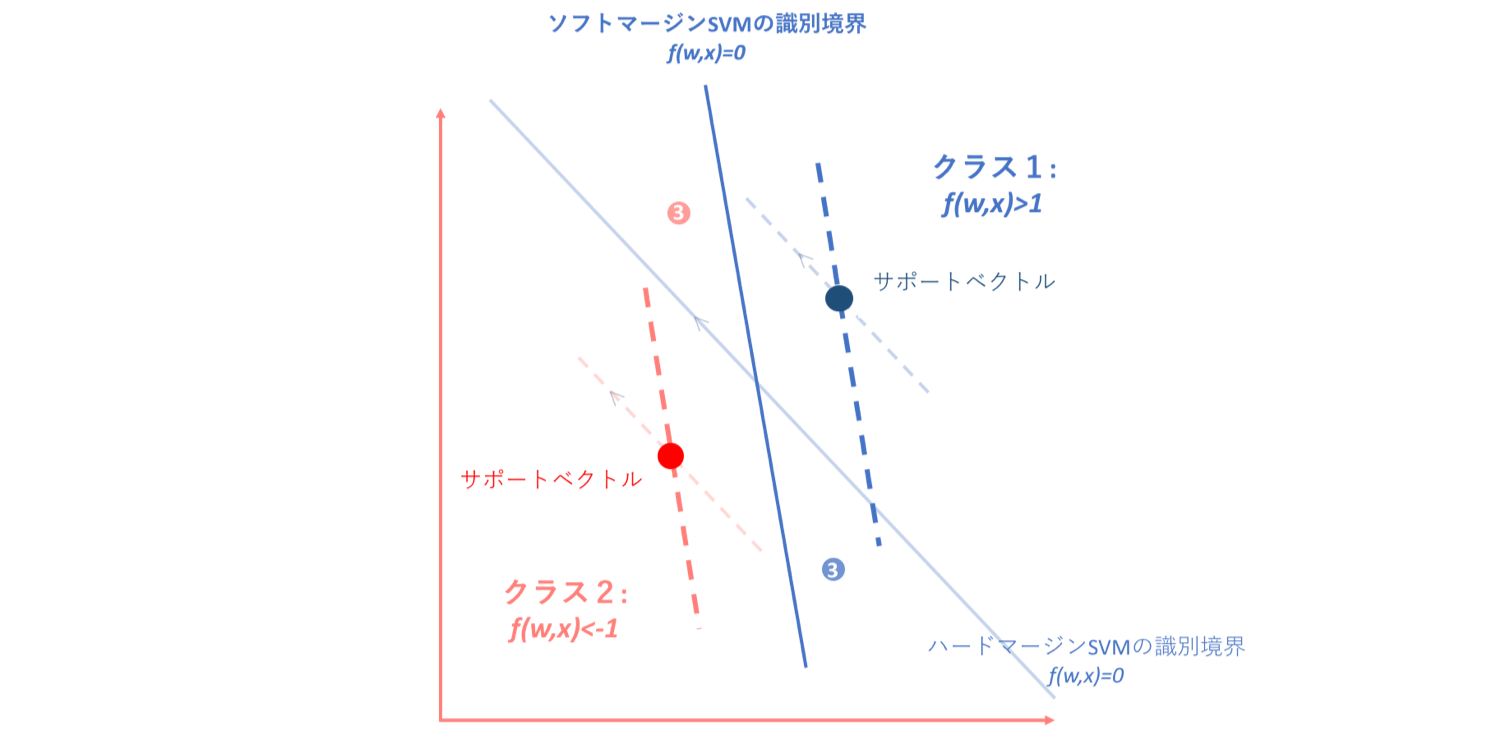
③ハードSVMおいては誤分類されているがソフトSVMにおいては正分類(ただし-1<f(w,x)<1)となるデータ
しかし、このような場合はどうでしょう。ハードマージンSVMにおいては誤分類されてしまっているのですが、ソフトマージンSVMにおいては正分類(ただし-1<f(w,x)<1)となっているデータ集合の場合です。この場合、これらのデータはサポートベクトルと識別境界の間に入り込んでしまっているのですが正分類ではあるため、パーセプトロン損失関数ではペナルティを与えることができません。
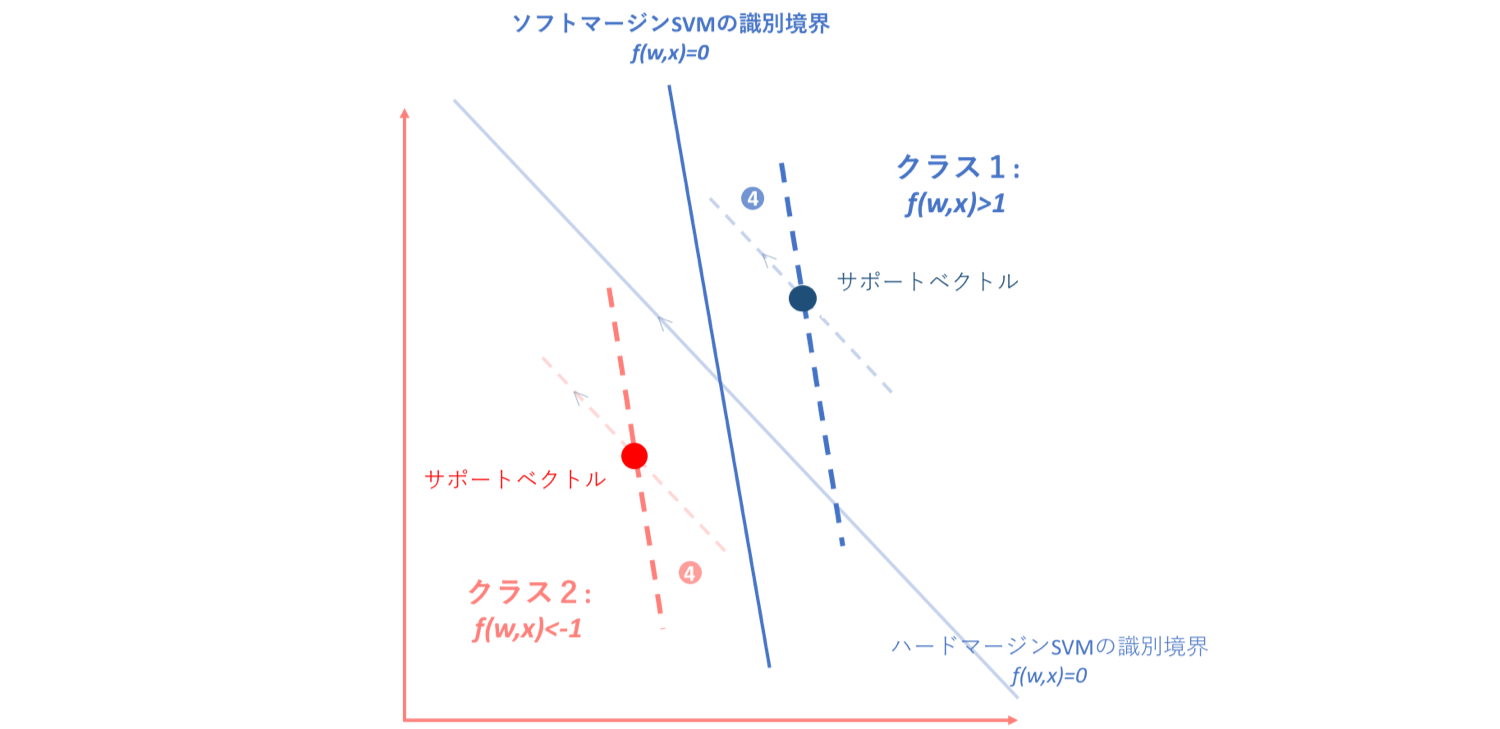
④ハードSVMにおいてはf(w,x)≧1 or f(w,x)≦-1だがソフトSVMにおいては正分類(-1<f(w,x)<1)となるデータ
また、このような場合もパーセプトロン損失関数ではペナルティを与えることができません。なぜなら、パーセプトロン損失関数では正分類されているかいないかでペナルティーを決定していたので、このようなサポートベクトルと識別境界の間にデータが存在するというナンセンスな状態に対してペナルティーを与えることができないからです。
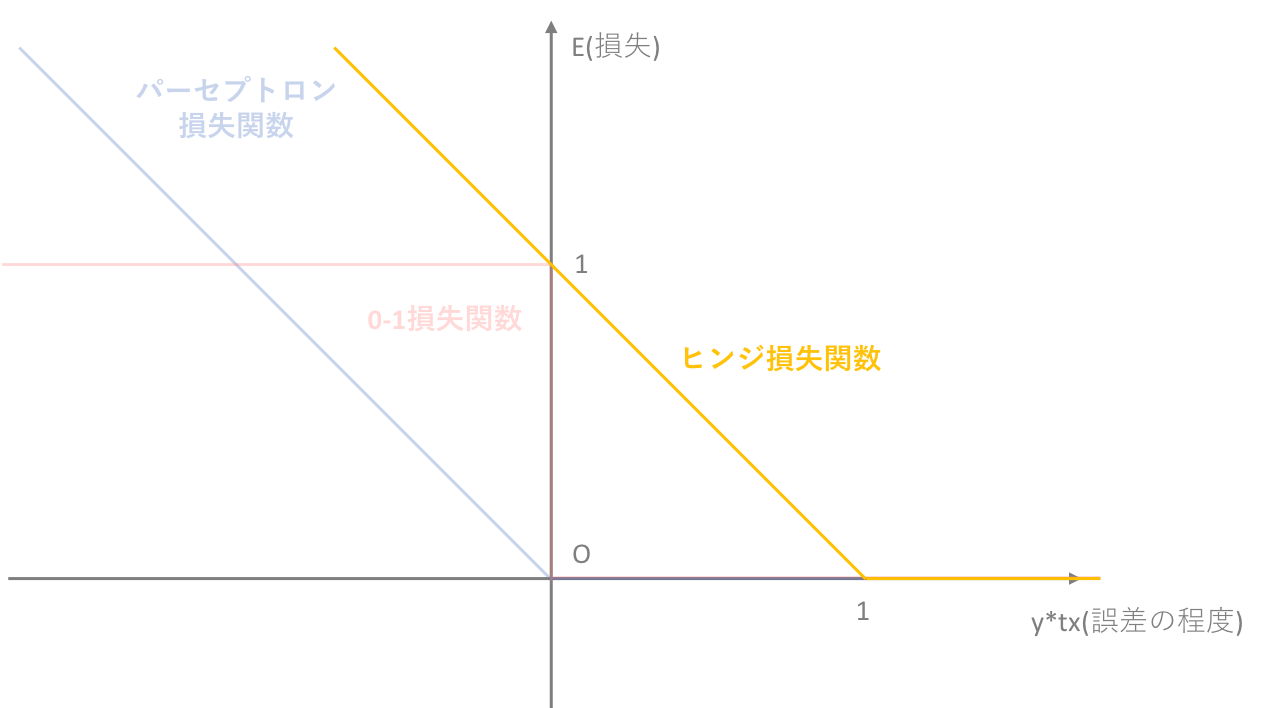
3.2.3. ヒンジ損失関数
以上の4つのグループの中で、①,②に関してはパーセプトロン損失関数で十分に対応できそうでした。しかし③,④についてはパーセプトロン損失関数では不十分だということが伺えます。③,④のデータ集合においてキーとなるのは、正分類されたデータが-1<f(w,x)<1内に入り込んでしまうということです。もちろんパーセプトロン損失関数を導入してこれは特異な例なので無視するということもできるのですが、このような"ギリギリ"のデータに対してもペナルティーを与え①のようなデータと差別化を計った方が、そのモデルの精度を向上させることにつながります。
よってこのような、正分類されているかどうかだけではなく、-1<f(w,x)<1内に入り込んでしまった正分類データにもペナルティーを与えるように導入された損失関数が、ヒンジ損失関数です。
ヒンジ損失関数は、以下のように示されます。
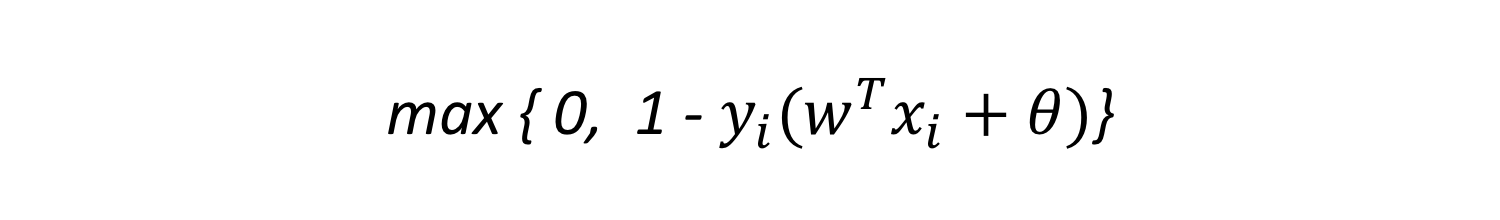
このように、ヒンジ損失関数はパーセプトロン損失関数を平行移動させることによって、ソフトマージンSVM特有のペナルティーにも対処することを可能としました。
3.3. 勾配法による解の導出
以上のフローよって導き出されたソフトマージンSVMの目的関数は、以下のようになります。
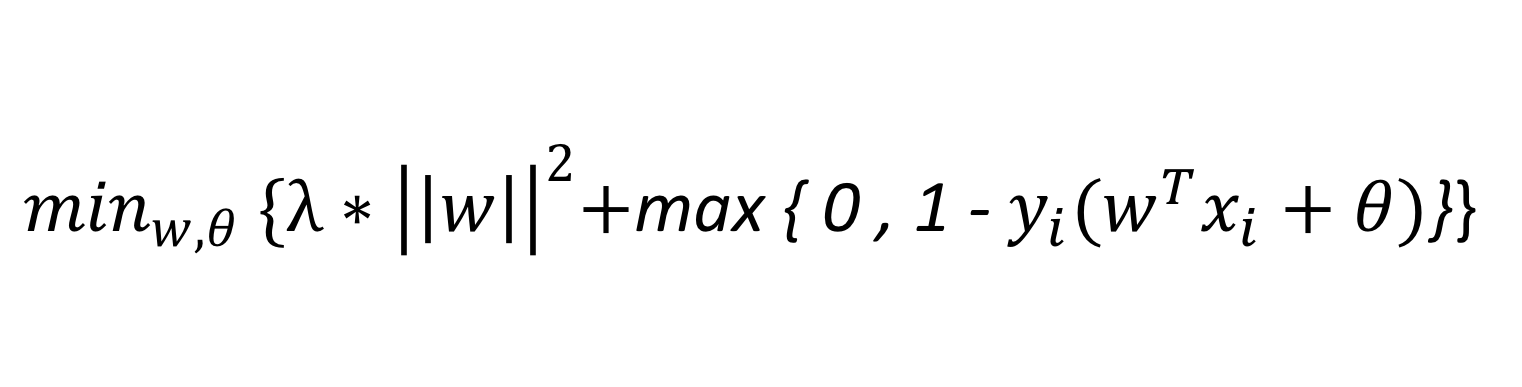
この数理計画問題の解き方は2種類あります。
3.3.1. 二次計画法
今回授業で習っていないので割愛させていただきます。以下のサイトに丁寧にまとめられていますのでご参照ください。
→今更のSVM(サポートベクトルマシン)
3.3.2. 確率的勾配降下法(stochastic gradient descent : SGD)
確率的勾配降下法のメリットやデメリット等詳しい説明については、勾配降下法の記事を別途作成しようと思っていますので、今回は簡単に説明させていただきます。(勾配降下法概要はこちら→初心者の初心者による初心者のための単純パーセプトロン)
確率的勾配降下法とは、用いる勾配を1つの訓練データから計算した勾配で近似する手法です。
確率的勾配降下法の基本アルゴリズムは以下のように書くことができるので、

これに基づいて、まずソフトマージンSVMの勾配を求めてみます。
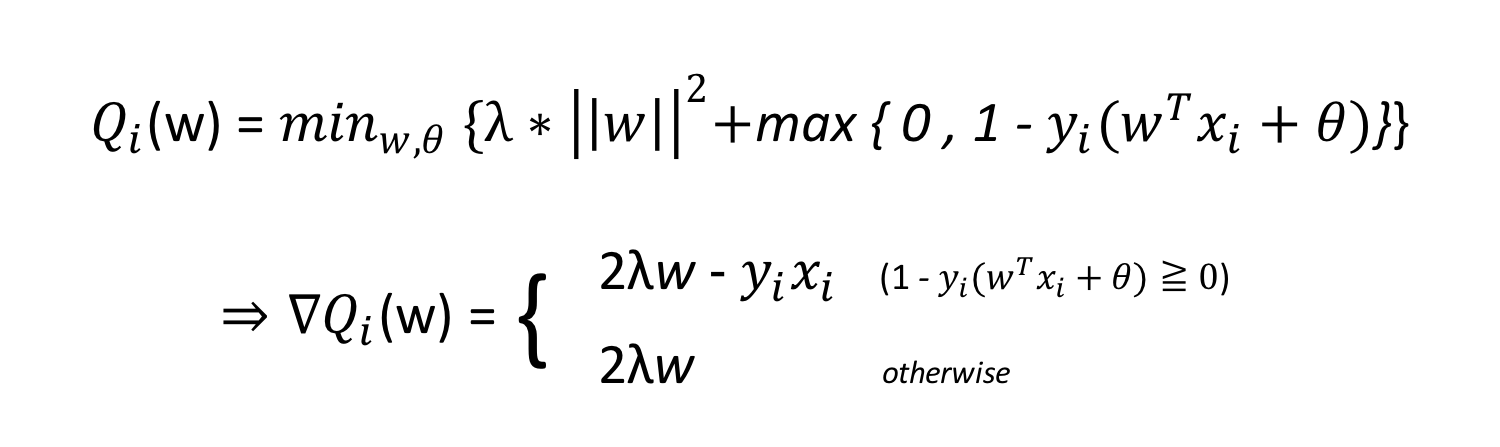
ソフトマージンSVMの目的関数勾配を求めることができたので、これを確率的勾配降下法のアルゴリズムに代入し、かつ勾配法のアルゴリズムそのものと組み合わせれば、以下が、ソフトマージンSVMの基本アルゴリズムとなります。
🔥初心者ゾーン突入🔥
分類器での分類結果が正解、つまり正分類かつf(w,x)≧1 or f(w,x)≦-1であっても重みを更新しなければいけないというのは感覚的には少し分かりづらく、どこまでも値が小さくなってしまうような気がしてしまいます。しかし、それはwを勝手に正の値のみで構成されていると勘違いしてしまうことが理由であり(私だけかもしれませんが)、けれどwは正という指定はまったくされていません。なので、wは正負どちらにもなり得ることで所定の回数極小値のまわりを小さく揺れ続けると考えると分かりやすいのではないでしょうか。
🔥初心者ゾーン脱出🔥
4. まとめ
5. 参照
ソフトマージンSVMのヒンジ損失最小化学習としての解釈とその実装
SVMにおける損失と正則化
SVMのマージン最大化についてしつこく考えてみる
ソフトマージンSVM
今更のSVM(サポートベクトルマシン)
初心者の初心者による初心者のための単純パーセプトロン
初心者の初心者による初心者のためのSVMハードマージン最大化