前回の続きです。
今回はRというより統計の基礎のお話をします。
ざっくりとですが理論に触ります。
また、最初の不偏分散と標本分散は今回は使いませんが雑学として置いておきます。
最後の方でRで使用していきます。
少しだけ用語紹介
- 母集団:その事象の元々の数値の集合みたいなイメージ
(例えば日本人の身長なら、日本人全員=1億人の身長のデータがこれ) - 標本:母集団から実際に調査して取ってきたデータ、一般に母集団を全て測ることは容易ではないので標本で統計をしていきます。
(日本人の身長を1000人調べたらこの1000人分のデータが標本)
標本分散と不偏分散
母集団と標本では、一般に分散が等しくはなりません。
そして標本から出した分散は母集団の分散に比べて若干小さくなることが知られています。
そこで、標本分散を母集団に近くなるように補正した分散のことを不偏分散といいます。
分散の式は高校で習ったように
$$ \frac{1}{n} \sum_{i=0}^n (X_i - X)^2 $$
ですね(すべての標本に対して平均値との差を取って、二乗したものの平均)。(Xは平均値)
そして標本の分散を標本分散といいます。しかしこれでは先程述べた通りに母集団の分散とずれがあるので、これを母集団と等しくなるように補正します。(ベッセルの補正)
やり方は簡単で $\frac{n}{n-1}$をかけるだけ!
要するに、平均を取るときに$n$で割る代わりに$n-1$で割ってしまうということです。
ということで、補正した分散は次のようになります。
$$ s^2 = \frac{1}{n-1} \sum_{i=0}^n (X_i - X)^2 $$
この補正した分散は標本の取り方によって偏りにくくなる(不偏になる)ので不偏分散といい、統計ではよくこれを使います。
この補正が正しいことの詳しい説明や証明が気になる方は、美しい高校数学の物語さんの「不偏標本分散の意味とn-1で割ることの証明」などが分かりやすいので参考にして下さい。
二項分布
10回コインを投げて、2回表が出る確率は、(コインが裏表が等しい確率で出ると仮定すると)高校でも習う式で$${}_{10} C _2 0.5^20.5^8$$であらわされます。
一般に、n回試行してr回、確率 θ の独立な事象が起きる確率はrの関数として
$$f(r) = {}_n C _rθ^r (1-θ)^{n-r}$$であらわされます。
このような確率分布を二項分布といいます。
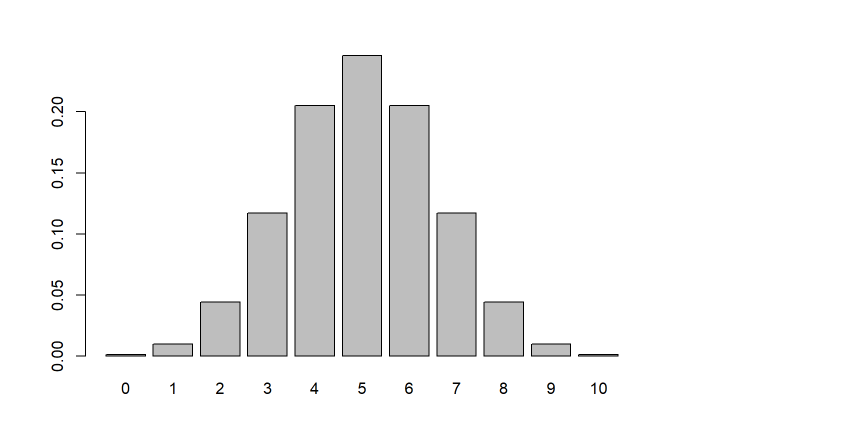
最初の例、θ = 0.5 の裏表が出る確率が等しいコインを10回投げて、r回表が出る確率をグラフにしてみます。
x = dbinom(0:10 , 10 ,p = 0.5)
barplot(x,names.arg = 0:10)
dbinomは二項分布に従って計算する関数で、0:10の範囲について計算してもらっています。
そしてそれをbarplot、つまり棒グラフで表示したのです。
結果を見ると当然ですが、10回試行して1回も表が出ない確率、10回表が出る確率は非常に小さいことが分かります。
帰無仮説
ではここで、10回投げてみて2回表が出たコインを考えます。
さて、このコインは本当に表と裏の出る確率が等しいのでしょうか?表の出にくい「インチキ」なコインではないのでしょうか?
ということで、ここでは帰無仮説というものを立てて、二項検定をしてこのコインがインチキなコインなのかを確かめてみます。
帰無仮説では、とりあえず表も裏も出る確率が50%ずつ(θ = 0.5)だと仮定します。
そしてこの仮説が間違っている(θは0.5ではない → 裏と表が出る確率は等しくない)かどうかを判定していくのです。
そのために、p値というものを算出して、その結果を解釈していきます。
p値を出してみる
p値とは、「帰無仮説が正しいと仮定したときに,観察されたこと以上に希なことが起きる確率」です。
このp値は、「今回の実験の結果(データ)そのものは、帰無仮説のもとでは本来何%の確率で出るものなのか」を示す値です。
もしこのp値が0.01だったら、今回の実験のデータは起こりにくいかも知れないけど1%の確率で起こることが起きただけなんだ、という意味になります。
...... 本当に__起こりにくいことがたまたま起きただけ__なんでしょうか?
このp値は、そもそも帰無仮説(裏表のどっちも同じ確率で出る正しい(フェアな)コインだという仮定)のもとに計算した値でした。
つまりp値 = 0.01 の解釈は二通りあり、
- 帰無仮説は正しかった(コインは正しい(フェアである))けど、たまたま1%(100回の実験に1回)の__珍しいことが起きてしまった__という解釈
- 1%なんて珍しいことが起きることは滅多に無いんだから、そもそも__計算の前提とした帰無仮説が間違ってた__という解釈
ここで5%という基準を決めます(5%水準)
p < 0.05 である時、つまり今回の実験が5%以下しか起きないことがたまたま起きてしまったということなら、実際にその5%という低い確率が起きたのはたまたまではなく元々の仮説が間違ってたからだ!と決めてしまう。
そうすれば、p < 0.05 の時、元の仮説(θ = 0.5 ,コインは正しい(フェア))が間違っていると言えるので、θ ≠ 0.5と言えそうだということが分かります。
具体的には、このコインは表と裏が出る確率が同じ正しい(フェアな)コインではなく、裏と表同じ確率で出るとはいえないインチキなコインだということができるのです。
帰無仮説を棄却する
このように最初に立てた「コインが正しい(今回はθ = 0.5、つまりコインがフェアである)」という仮定(帰無仮説)を否定することを「帰無仮説は棄却された」と言ったり、「帰無仮説からの外れが統計的に有意である」と言ったりします。
逆に、 p > 0.05 だった時には「帰無仮説は棄却されなかった」という結論以上は何も出す必要はありません。
注意すべきなのは、このとき、「帰無仮説(θ=0.5)が証明された」とは言ってはいけないことです(重要)。
これは、今回の検定では「正しくないとは言えない」だけで「正しいとも言えない」からなのです。
このように、「帰無仮説を棄却できる」のに対して「帰無仮説を証明する」ことはできません。
言い換えると、インチキを指摘することはできても、インチキでないことを証明することはできません。
これを検定の非対称性と言います。
Rで計算してみる
前置きが長くなりました、ようやくRでさっきのコインの話を計算させてみましょう!
10回中2回しか表の出なかったコインのp値を求めてみます。
まずは帰無仮説(確率θ = 0.5)を仮定したうえで、binom.test()関数を使うことで求められます。
p = binom.test(x = 2 , n = 10,p = 0.5)
p
##
## Exact binomial test
##
## data: 2 and 10
## number of successes = 2, number of trials = 10, p-value = 0.1094
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
## 0.02521073 0.55609546
## sample estimates:
## probability of success
## 0.2
結果として p-value = 0.1094 であることが分かります。
つまり、p は 0.05よりも大きかったので、「帰無仮説は棄却されなかった」のです。
この2回しか表の出ないコインは、この5%水準上ではインチキであるとまでは言い切れないのです。
しかし、やはり「帰無仮説が証明されたわけではない」ことは忘れてはいけませんよ(重要)。
具体的には、この結果は別にこのコインがインチキではないことを証明したわけではなく、インチキであるとは言い切れないだけなのです。
そしてこの帰無仮説(他の仮説もあります)を仮定して、p値を計算して、この仮説を棄却したり棄却出来なかったりすることを統計学的検定(仮説検定)と言います。
他の例で試してみる
ここに5%の確率で当選と謳っている懸賞があったとします。
友達と協力してこの懸賞に応募しまくって、200通のはがきを出したのですが、当たったのは2人だけでした。
これでは当たる確率は2/200なので1%ではありませんか!!
と激怒したのでインチキじゃね?と二項検定をしてみます。
今回は公式発表が5%なので、θ = 0.05という帰無仮説を立ててみます。
binom.testした結果からp値だけを出したいときは$p.valueをつければOKです。
result = binom.test(x = 2, n = 100, p = 0.05)
result$p.value
## [1] 0.2462235
p = 0.2462235 でした。0.05より大きいのでこれでは「帰無仮説が棄却される」とは言えなそうです、残念。
しかし何度でも言いますが、これはインチキをしている証明にもインチキをしていない証明にもなりません。
ただ、「インチキをしているとは言い切れない」だけなのです。
pハッキング
ここに本当に裏表が出る確率が等しい、正しくてフェアなコインがあるとしましょう。
そして本当は正しいθ=0.5という帰無仮説をたてます。
10回投げる実験を1回やってみました。
4回表が出ました、統計学的検定(この場合は二項検定)をしてみます。
result = binom.test(x = 4 , n = 10, p = 0.5)
result$p.value
## [1] 0.7539063
これでは、0.05以下とはとてもではないけど言えないのでどの結論も出せないです。
ということでもう一度同じ実験をしてみます。
今度は7回表が出ました、計算してみましょう。
result = binom.test(x = 7 , n = 10, p = 0.5)
result$p.value
## [1] 0.34375
これでもp値は0.34、p < 0.05とはとても言えないのでダメそうです...
ということで5回同じ実験をした後、やっと1回だけしか表が出なかった実験になったとします。
さあウキウキで計算します。
result = binom.test(x = 1 , n = 10, p = 0.5)
result$p.value
## [1] 0.02148438
これでp値は0.02です。帰無仮説が棄却出来ました!!!!(は?)
よってこのコインは表の出にくいインチキです!!!!!!(は?)
このように、検定の回数を繰り返したり、他にも様々な操作をしたりすることでp値は変わってしまいます。
そして、大体論文としてまとめられているのはp値が0.05よりも小さかった時で、そうでない場合の論文は発表されないことが多いです。(出版バイアスと言います)
そして、今回のようなp値が0.05になるまで何度も実験をして無理やり有意性などというものを示すようなことを多重検定といいます。
また、多重検定やその他の方法などで不適切にp値を操作することを悪事をpハッキングといいます。
やっちゃだめですよ。
まとめ
- 帰無仮説は「コインが正しい(フェアである)」、や「懸賞が5%で当たる」などの、最初に建てる仮定です。(棄却することを目指します)
- p値は「観察された以上に希なことが起きる確率」
- p < 0.05 なら帰無仮説を棄却出来て、統計的に有意差があると言えます。
- p > 0.05 なら帰無仮説を棄却出来ませんが、帰無仮説を証明もしていません。なんの結論も出ないのです。
- p値は不正に操作出来てしまうものですが、それらの不正操作「pハッキング」を行わないようにしましょう。
さいごに
今回は二項分布に従う事象の統計学的検定(今の場合は二項検定)について基礎の基礎を解説しました。
今回の検定手法のようなものを統計的仮説検定といいます。
この統計的仮説検定はこの他にもたくさんあり、それぞれの場合に適切な検定が存在します。
最後に見たように、p値はその試行回数などで操作でき、悪意を持ったり適切に扱わなかったりするとすぐに参考にならないデータになりえます。
またこのことは非常に多くの議論があり、実際に論文として発表する際に使う場合はよく調べて、適切な説得力を持つように使用しましょう。
詳しいことは「仮説検定の判断をp値でする危険性」などを参照してください。
しかし、このp値の扱いについてはこのほかの様々な検定に用いられており、この意味を理解しておくことは大事なので紹介しました。
今回は統計学の基礎の解説が長くなり、Rを使うフェーズはほとんど無かったので次回はもう少しRの機能を使った記事にしたいと思います。
一応次回はt検定という検定手法を紹介するつもりです。
長文になりましたがありがとうございました。
ご指摘頂きました
@__DielsAlder_ 様
@konandoiruasa 様
曖昧な表現・定義や謬りの修正を提案、ご教示いただきました、ありがとうございました!
次はもう少し正確な表記に心がけたいと思います...
参考にしました
- 奥村晴彦「Rで楽しむ統計」(共立出版、2016年)
- 「標本分散と不偏分散」(https://stats.biopapyrus.jp/stats/var.html 、2019年閲覧)
統計学の解説をもっと短く、分かりやすくかけるようになりたいものですね...
「だ・である」と「です・ます」の使い分けを失敗した感じがあります...