はじめに
Chandra の HETG(High Energy Transmission Grating)は、ACIS-S に透過型の回折格子を挿入することで、高分解能の X 線分光を実現する観測方式です。
しかし、公式ドキュメントは情報量が多く、初めて HETG を使う場合は全体像をつかみにくいところがあります。
そこで本記事では、HETG の基本的なしくみを 物理的なイメージ と 実際の観測画像 の両面から整理し、できるだけ直感的に理解できるようにまとめていきます。
後半では、実際の観測データを使って
「HETG ではどのように画像が写り、どこに情報が詰まっているのか」
を、Chandra の標準ツールである CIAO を使いながら一緒に確認していきます。
HETG をこれから使い始める方が、気持ちよく理解を深められる記事になれば幸いです。
HETG の基本構造
HETG では ACIS-S の前に透過型グレーティングを挿入します。
模式図は以下のようになっています。
(公式より引用)
ポイントは次のとおりです:
- 入射した X 線の一部は回折格子で方向を変えられ、±1 次光(first orders) に分散される
- 回折されなかった光は 0 次光(zeroth order) として検出される
- グレーティングが遮蔽物として働くため、0 次光の有効面積は大きく低下する
なお、0 次光は有効面積が小さくなる一方で、パイルアップを抑えられるという利点もあります。そのため、明るい天体ではむしろイメージングに有効な場合もあります(例:Sakai et al. 2025)。
また、MEG(Medium Energy Grating) と HEG(High Energy Grating) の 2 種類の格子が積層されていることが分かります。
また、HEG 側の格子ピッチ(溝の間隔)がより細かく作られていることも図から確認できます。
回折の基本式
回折格子に入射した光子の回折角 $\beta$ は次式で決まります。
\sin\beta = m \frac{\lambda}{p}
- $\beta$:回折角
- $m$:次数($…−2,\, −1,\, 0,\, +1,\, +2\, …$)
- $\lambda$:波長
- $p$:溝の周期
この式から読み取れること:
- 周期 $p$ が小さいほど、同じ $\lambda$ に対して $\beta$ が大きい(=よく分散される)
- $m = ±1$ がもっとも効率が高い
- 高次($±2$ 以上)は光子数が少なく、実務ではほぼ使わない
概念だけだと実感が湧きにくいので、実際の観測画像を見てみます。
ほぼ点源を観測した場合、HEG/MEGの ±1 次光は次のように 4 本の線として現れます。
(公式より引用)
先ほどの回折の式を使うと、観測画像の構造が理解できます。
波長が大きい(=低エネルギー)ほど回折角 $\beta$ は大きくなり、観測画像では ±1 次光が外側へ広がります。
また、HEG は MEG より格子ピッチが細かいため、同じ波長でも回折角が大きくなります。
このとき、わずかな波長差 $\Delta λ$ に対して生じる像上の位置の違い $\Delta x$ が MEG よりも大きくなるため、
エネルギーの変化をより鋭敏に検出でき、結果として HEG の方が高い分解能を持つことになります。
ここで、後半の 有効面積の確認の節 で詳しく比較しますが、
HETG における 有効面積(ARF)がどのように決まるか を、この段階で一度整理しておきます。
HETG の ARF は単純に「分散が大きい・小さい」だけで決まるわけではなく、実際には複数の要因が絡み合っています。主な要因としては、
- 格子構造そのものの透過率の違い
- 回折効率のエネルギー依存性
- CCD チップ間のギャップによる幾何学的ロス
(このため +1 / −1 でわずかな差が生じることもある)
などが挙げられます。
こうした要因が合わさった結果として、
- HEG:分解能は高いが、低エネルギー側では有効面積が小さくなりやすい
- MEG:分解能はやや低いものの、低エネルギー側まで比較的良くカバーできる
といった実用上の特性が生まれています。
実際に HETG 観測データで確認する
ここからは、実際の Chandra/HETG 観測(SS 433, ObsID 106)を例に、
HEG と MEG の 1 次光スペクトルがどのように得られるのかを一緒に見ていきます。
CIAO のセットアップ方法は こちらの記事 にまとめていますので、
必要に応じてそちらも参考にしていただければと思います。
本記事では CIAO v4.17 を使用しています。
データ取得と再処理
まずはデータを取得し、標準の再処理を行います。
ここは特に難しいところはなく、コマンドをそのまま実行するだけです。
download_chandra_obsid 106
chandra_repro 106 outdir=""
これで 106/repro の中に、グレーティング解析に必要なファイル一式が揃います。
観測画像をざっと確認する
必須ではありませんが、HETG の構造がイメージしやすくなるので、
軽く DS9 で画像を見てみましょう。
acisf00106_repro_evt2.fits を DS9 で開き、scale → log を選ぶと見やすくなります。
bin 8(CCD 全体)
6 枚の ACIS-S チップが表示されていて、それぞれに領域(region)が描画されています。
これは CIAO が HETG 観測時に自動で 0 次光や ±1 次光の領域を分かりやすく示してくれるデフォルト仕様です。
bin 1(中心の拡大)
中央の円が 0 次光(zeroth order)、斜めに伸びる 4 本の線が HEG / MEG の ±1 次光 です。
(bin=1 のとき縮小しても描画が更新されないことがありますが、これは DS9 の描画コストによる仕様だと思います。)
HETG 解析では ±1 次光は基本的にまとめて使うため、HEG / MEG と ± の向きを厳密に覚える必要はありません。
ただし、先ほどの回折の式を思い出すと、
0 次光に近い方が MEG、より外側に広がる方が HEG
という対応関係だけは図からも読み取れます。
この関係を軽く頭に置いておくと、HETG 画像と物理のつながりが見えてきて、観測データを眺めるときに少し楽しくなると思います。
1 次光スペクトルの確認
再処理が終わると、106/repro/tg にはすでに HEG/MEG の 1 次光スペクトルが生成されています。
$ ls 106/repro/tg
acisf00106_repro_heg_m1.arf acisf00106_repro_heg_p1.arf
acisf00106_repro_meg_m1.arf acisf00106_repro_meg_p1.arf
...
-
.pha:観測スペクトル -
.arf:有効面積(Auxiliary Response File) -
.rmf:エネルギー応答(Redistribution Matrix File) -
_bkg.pha:背景スペクトル
この時点で スペクトル解析に必要な基本セットはほぼ揃っています。
あとは、HETG 解析でよく行う ±1 次光の統合を行うだけです。
±1 次光を足し込む
HETG では +1 と −1 の応答はほぼ同等であるため、
±1 次光をまとめて扱い、統計を 2 倍にするのが一般的です。
まずは出力先を作成し、
$ cd 106/repro
$ mkdir merge_tg
次に combine_grating_spectra を実行します。
combine_grating_spectra \
infile=acisf00106_repro_pha2.fits \
outroot=merge_tg/ \
add_plusminus=yes \
arf="tg/*arf" \
rmf="tg/*rmf"
これだけで HEG と MEG の ±1 が自動的にまとめられます。
足し込まれたスペクトルの確認
$ ls merge_tg
combo_heg_abs1.arf combo_meg_abs1.arf
combo_heg_abs1.pha combo_meg_abs1.pha
combo_heg_abs1.rmf combo_meg_abs1.rmf
combo_heg_abs1_bkg.pha combo_meg_abs1_bkg.pha
...
combo_heg_abs1.* と combo_meg_abs1.* がHEG / MEG の ±1 次光を足し込んだ結果です。
これでスペクトル解析の準備は完了です。
次のステップ:XSPECでフィッティングへ
今回まとめた .pha(スペクトル)、.arf(有効面積)、.rmf(応答) を使えば、そのまま XSPEC でスペクトルフィッティング に進めます。
フィッティングの具体的な手順や bin まとめの方法は、
山田さんの記事 が大変わかりやすいので参考にしてください。
補足
データ解析では、公式ドキュメントをそのまま信じすぎない ことも大切だと思います。
実際、ARF や RMF などのレスポンスファイルは経年変化や較正更新の影響を受けていますし、「昔の論文の特性」と「いま手元にあるレスポンス」が完全に一致しているとは限りません。
そのため、自分がいま扱っているデータが実際にどのような応答をしているのか可視化して確かめることは、デバッグの観点でも、理解を深めるという意味でも、とても有効だと思います。
ここでは、HETG の ARF・RMF を実際に可視化して確認してみます。
可視化スクリプトの詳細は以下の記事にまとめているので、興味があればあわせてご覧ください。
有効面積(ARF)の確認
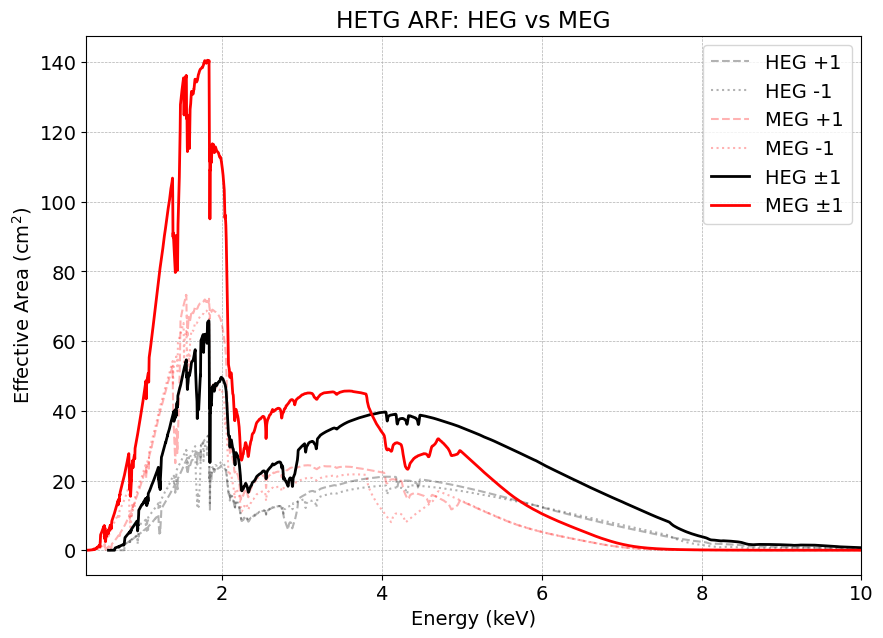
「HEG は低エネルギー側で有効面積が小さい」とよく言われますが、まずは本当にそうなのか確認してみましょう。
さらに、足し込み(±1の combine)前後で ARF がどう変わるか も見ておくと理解が深まります。
コードはこちら
from astropy.io import fits
import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 14
def load_arf(file_path):
with fits.open(file_path) as hdul:
arf = hdul[1].data
e_mid = (arf["ENERG_LO"] + arf["ENERG_HI"]) / 2
area = arf["SPECRESP"]
return e_mid, area
# ===== 個別 ObsID =====
tg_path = "../106/repro/tg/"
heg_p1_arf = tg_path + "acisf00106_repro_heg_p1.arf"
heg_m1_arf = tg_path + "acisf00106_repro_heg_m1.arf"
meg_p1_arf = tg_path + "acisf00106_repro_meg_p1.arf"
meg_m1_arf = tg_path + "acisf00106_repro_meg_m1.arf"
# ===== マージ後 (abs1) =====
merge_path = "../106/repro/merge_tg/"
heg_abs1_arf = merge_path + "combo_heg_abs1.arf"
meg_abs1_arf = merge_path + "combo_meg_abs1.arf"
# ===== データ読み込み =====
e_heg_p1, a_heg_p1 = load_arf(heg_p1_arf)
e_heg_m1, a_heg_m1 = load_arf(heg_m1_arf)
e_meg_p1, a_meg_p1 = load_arf(meg_p1_arf)
e_meg_m1, a_meg_m1 = load_arf(meg_m1_arf)
e_heg_abs1, a_heg_abs1 = load_arf(heg_abs1_arf)
e_meg_abs1, a_meg_abs1 = load_arf(meg_abs1_arf)
# ===== プロット =====
plt.figure(figsize=(10, 7))
# 個別 ObsID (±1)
plt.plot(e_heg_p1, a_heg_p1, label="HEG +1", color="k", linestyle="--", alpha=0.3)
plt.plot(e_heg_m1, a_heg_m1, label="HEG -1", color="k", linestyle=":", alpha=0.3)
plt.plot(e_meg_p1, a_meg_p1, label="MEG +1", color="r", linestyle="--", alpha=0.3)
plt.plot(e_meg_m1, a_meg_m1, label="MEG -1", color="r", linestyle=":", alpha=0.3)
# merge_tg (abs1)
plt.plot(e_heg_abs1, a_heg_abs1, label="HEG ±1", color="k", linewidth=2)
plt.plot(e_meg_abs1, a_meg_abs1, label="MEG ±1", color="r", linewidth=2)
plt.xlabel("Energy (keV)")
plt.ylabel("Effective Area (cm$^2$)")
plt.title("HETG ARF: HEG vs MEG")
plt.grid(True, linestyle="--", linewidth=0.5)
plt.legend()
plt.xlim(0.3, 10)
plt.savefig("hetg_arf_comparison.png", bbox_inches='tight')
plt.show()
可視化すると、HEG は低エネルギー側で ARF が小さいこと、±1 の違いがわずかにあること、そして combine 後はほぼ 2 倍になって統計が良くなっていることを確認できます。
言い換えると、MEG の強みは低エネルギー側での高い有効面積にあり、実際の観測では HEG・MEG の間で自然な棲み分けが生じていることが分かります。
HEG は高分解能を担い、MEG は低エネルギーでの感度を補う──こうした役割分担が HETG 全体の性能を支えていると言えます。
エネルギー分解能(RMF)の確認
RMF は、ある入射エネルギーがどの出力チャンネルに分布するかを示す応答行列です。
HETG の場合、HEG と MEG の RMF は近いものの、微妙に形が異なります。
ここでは ±1 を足し込んだ HEG / MEG の RMF を可視化してみます。
| HEG | MEG |
|---|---|
 |
 |
コードはこちら
RMFのチャンネル番号のずれに注意
Chandra と XRISM を比較していて気づいたのですが、RMF の F_CHAN の開始インデックスが 1 ずれている ようです。
Chandra は 1 始まり、XRISM は 0 始まりとなっていました。
原因の深掘りはしていませんが、本記事で示したスクリプトは Chandra/HETG 用に調整 したものです。
XRISM で使う場合は注意してください。
import os
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
from matplotlib.ticker import AutoLocator, AutoMinorLocator
import astropy.io.fits as fits
# matplotlibのグローバル設定(プロットの見た目を統一)
plt.rcParams['xtick.direction'] = 'in' # x軸の目盛りを内向きに設定
plt.rcParams['ytick.direction'] = 'in' # y軸の目盛りを内向きに設定
def construct_rmf_matrix(filename):
"""
RMFからレスポンスマトリックスを構築する関数(Chandra用)。
Parameters:
filename (str): FITSファイルのパス。
Returns:
dict: 構築されたレスポンスマトリックスと関連データを含む辞書。
"""
with fits.open(filename) as f:
# 必要なデータを抽出
f_chan = f[1].data['F_CHAN']-1 # チャンネルの開始位置(Chandraは1始まり、XIRMは0始まりなので注意)
n_chan = f[1].data['N_CHAN'] # チャンネルの数
compressed_matrix = f[1].data['MATRIX'] # 密な(非ゼロのみの)マトリックスデータ
in_ene_lo = f[1].data['ENERG_LO'] # 入力エネルギー下限
in_ene_hi = f[1].data['ENERG_HI'] # 入力エネルギー上限
out_ene_lo = f[2].data['E_MIN'] # 出力エネルギー下限
out_ene_hi = f[2].data['E_MAX'] # 出力エネルギー上限
# フルレスポンスマトリックスの次元を決定
num_in_ene_bins = len(in_ene_lo) # 入力エネルギーのビン数(行数)
num_out_ene_bins = len(out_ene_lo) # 出力エネルギーのビン数(列数)
# フルレスポンスマトリックスを構築
matrix = np.zeros(shape=(len(in_ene_lo), len(out_ene_lo)), dtype='float32')
for j in range(f_chan.shape[0]):
tot_n = 0
for f, n in zip(f_chan[j], n_chan[j]):
# 密なデータをフルマトリックスに埋め込む
matrix[j, f:f + n] = compressed_matrix[j][tot_n:tot_n + n]
tot_n += n
return matrix, in_ene_lo, in_ene_hi, out_ene_lo, out_ene_hi
def binning_out_ene(matrix, bin_size, ene_lo, ene_hi):
"""
2D配列のx方向(列方向)でビニングを実行し、出力エネルギー境界もビニングする関数。
Parameters:
matrix (numpy.ndarray): 2D入力配列。
bin_size (int): 列方向でのビンサイズ(足し込む列数)。
ene_lo (numpy.ndarray): 出力エネルギーの下限配列。
ene_lo (numpy.ndarray): 出力エネルギーの上限配列。
Returns:
tuple:
numpy.ndarray: ビニングされた2D配列。
numpy.ndarray: ビニングされた出力エネルギー境界。
"""
# 必要な列数を計算し、ゼロ埋めで配列を拡張
num_cols = matrix.shape[1]
padding = (bin_size - (num_cols % bin_size)) % bin_size # 不足分の列数を計算
padded_matrix = np.pad(matrix, ((0, 0), (0, padding)), mode='constant', constant_values=0)
# 配列をリシェイプしてビンごとに合計
new_shape = (matrix.shape[0], padded_matrix.shape[1] // bin_size, bin_size)
binned_matrix = padded_matrix.reshape(new_shape).sum(axis=2)
# 出力エネルギー境界をビンサイズでサンプリング
binned_out_ene_edges = np.append(ene_lo[::bin_size], ene_hi[-1])
return binned_matrix, binned_out_ene_edges
# インプットファイル名
# HEGを使う場合
rmf_filename = '../106/repro/merge_tg/combo_heg_abs1.rmf'
out_matrix_filename = f'chandra_heg_abs1_matrix.png'
out_6400ev_filename = f'chandra_heg_abs1_6400ev.png'
# MEGを使う場合
# rmf_filename = '../106/repro/merge_tg/combo_meg_abs1.rmf'
# out_matrix_filename = f'chandra_meg_abs1_matrix.png'
# out_6400ev_filename = f'chandra_meg_abs1_6400ev.png'
# RMFデータの読み込みと構築
matrix, in_ene_lo, in_ene_hi, out_ene_lo, out_ene_hi = construct_rmf_matrix(rmf_filename)
# エネルギー境界を計算
in_ene_edges = np.append(in_ene_lo, in_ene_hi[-1])
out_ene_edges = np.append(out_ene_lo, out_ene_hi[-1])
# プロット作成
fig, ax = plt.subplots(figsize=(8, 6))
c = ax.pcolormesh(
out_ene_edges,
in_ene_edges,
matrix,
cmap='turbo',
norm=LogNorm(vmin=1e-6, vmax=0.3)
)
ax.set_xlabel('Output (keV)')
ax.set_ylabel('Input (keV)')
ax.set_aspect('equal')
fig.colorbar(c, ax=ax, label='Probability')
# 軸の設定とグリッド
ax.xaxis.set_major_locator(AutoLocator())
ax.xaxis.set_minor_locator(AutoMinorLocator())
ax.yaxis.set_major_locator(AutoLocator())
ax.yaxis.set_minor_locator(AutoMinorLocator())
ax.grid(which='major', color='gray', linestyle='--', linewidth=0.5)
ax.grid(which='minor', color='lightgray', linestyle=':', linewidth=0.3)
# ファイル名をタイトルに設定し保存
base_matrix_filename = os.path.splitext(out_matrix_filename)[0]
ax.set_title(base_matrix_filename)
fig.savefig(out_matrix_filename, bbox_inches='tight')
plt.show()
# ==========================================
# 6.4 keV の出力レスポンスを取り出してプロット
# ==========================================
target_E = 6.4
# 6.4 keV が属する入力ビンを検索
idx = np.where((in_ene_lo <= target_E) & (in_ene_hi > target_E))[0][0]
# 対応する出力エネルギー応答(1D)
response_64keV = matrix[idx]
# プロット
fig = plt.figure(figsize=(7,5))
plt.step(out_ene_edges[:-1], response_64keV, where='post', lw=1.5)
plt.xlim(6.2, 6.6)
plt.ylim(None, 0.3)
plt.xlabel("Output Energy (keV)")
plt.ylabel("Probability")
plt.grid(True, alpha=0.5)
# ファイル名をタイトルに設定し保存
base_6400ev_filename = os.path.splitext(out_6400ev_filename)[0]
plt.title(base_6400ev_filename)
fig.savefig(out_6400ev_filename, bbox_inches='tight')
plt.show()
上図の見方としては、縦軸が入射エネルギー、横軸が観測されたときの出力エネルギーに対する確率分布を表しています。
この図から、HEG / MEG のどちらも 分解能(ピークの広がり)がエネルギーとともに変化し、特に高エネルギー側では広がりが大きくなる傾向があることがわかります。
このあたりの詳細は専門的で数式も複雑なため、詳しい仕組みや数式展開に興味がある方は、公式ドキュメントの Fig. 8.19 や “LRF: Dispersion Direction” 節 をご覧ください。
ところで、HEG は MEG に比べて回折格子ピッチが細かく作られているため、原理的には HEG のほうがエネルギー分解能に優れています。
実際にその違いがどの程度なのか確認するため、6.4 keV 入射時の RMF における出力エネルギーの確率分布を比較します:
| HEG | MEG |
|---|---|
 |
 |
ここで注意点として、RMF の縦軸は「その bin に入る確率」であり、HEG と MEG で bin 幅が異なるため、縦軸の絶対値は比較できません(今回の図は RMF の生データをそのまま表示しているため、このような形になります)。
そのため、分解能を比較するときは ピーク幅(FWHM)だけを見れば十分で、HEG の方が MEG よりも確かにシャープであることがわかります。
まとめ
本記事では、HETG の基本構造から回折のしくみ、そして HEG / MEG の違いが観測画像やレスポンスにどのように現れるのかを整理しました。
押さえておきたいポイントは次の 3 つです。
-
HEG と MEG の性能差は主に格子ピッチから生まれ、それぞれの“ウリ”を決定づけている。
- HEG の強み:高エネルギー分解能。特に高エネルギー帯域でシャープなスペクトルが得られる。
- MEG の強み:低エネルギー側での高い有効面積(感度が良い)。
-
ARF(有効面積)は透過率・回折効率・CCD ギャップなど複数要因が効くため、結果として HEG は低エネルギー側で有効面積が落ち、MEG がその領域を自然に埋める形になる。
-
±1 次光は実務上ほぼ同等の応答を持つため、統合して扱うことで統計が大きく向上する。
HETG の解析は最初は少しとっつきにくいですが、しくみが腑に落ちてくると、
HEG と MEG のそれぞれの強みが互いを補い合い、天体を丁寧に見ていくための美しいバランスを作っていることが実感できると思います。
(これは XRISM で Resolve がエネルギー分解能を担い、Xtend が光度変化や空間分解能を補う役割と似ています。)
本記事が、これから HETG を使ってみたい方や、Chandra がイメージだけでなく分光でも大きな力を発揮することを知るきっかけになれば嬉しく思います。
関連記事