はじめに
三次元回転の最適化に親しむために、Pythonで3次元ポーズ調整のプログラムを書きました。
ポーズ調整の結果(青が最適化前で、赤が最適後です)
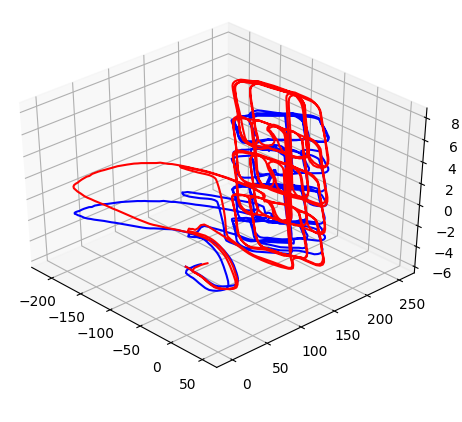
parking-garage.g2o
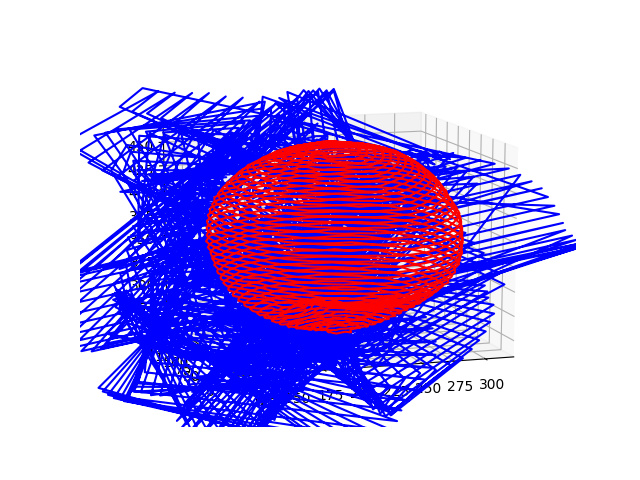
sphere2200_guess.g2o
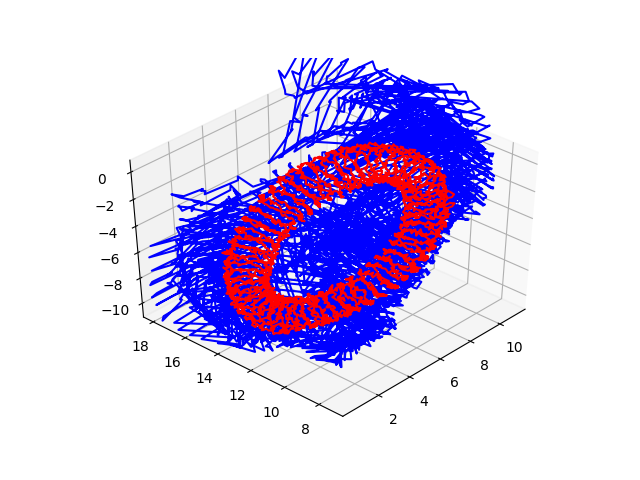
torus3d_guess.g2o
ポーズ調整とは
ポーズ調整(pose adjustment)はGraph-Based SLAM(Simultaneous Localization and Mapping)の一種で、軌跡のみを最適化するものです。
Graph-Based SLAMは最新の位置姿勢だけではなく、軌跡全てと地図を最適化する完全SLAMの一種で、グラフ構造を用いるのでGraph-Basedという名が付いています。
Graph-Based SLAMや完全SLAMに関して詳しくは以下の記事を参照ください。
Graph-Based SLAMを用いた軌跡推定シミュレーション
また、より深くGraph-Based SLAMやポーズ調整を知りたい方はネット資料では『移動ロボットの環境認識―地図構築と自己位置推定』、書籍では『SLAM入門』の4章4節などを参照していたたければと思います。
実装
記号
$i,j$:インデックス
$\boldsymbol{p}=[x,y,z]$:位置ベクトル
$\boldsymbol{\omega}=[\omega_x,\omega_y,\omega_z]$:回転ベクトル
$\boldsymbol{q}=[q_w,q_x,q_y,q_z]$:クォータニオン
$\boldsymbol{x_i}=[x_i,y_i,z_i,\omega_{xi},\omega_{yi},\omega_{zi}]$:最適化する位置姿勢
$\boldsymbol{x=[x_0,x_1,...]}$:最適化する軌跡
$\boldsymbol{f(x_i,x_j)}$ : $\boldsymbol{x_i}$-$\boldsymbol{x_j}$間の相対姿勢
$\boldsymbol{d_{i,j}}$:オドメトリまたはスキャン・マッチング等で得られたi-j間の相対位置姿勢
$\boldsymbol{e_{ij}=f(x_i,x_j)-d_{ij}}$:誤差関数
$\boldsymbol{J_{ij}=∂e_{ij}/∂x}$:ヤコビアン
$F(x)= \Sigma e_{ij}^T \Omega^{-1} e_{ij}$:誤差関数の総和
$\boldsymbol{\Omega}$:共分散行列
$\Sigma$:総和
$T$:転置
$\otimes$:クォータニオンの乗法演算子
実装概要
ポーズ調整のアルゴリズム自体は「Graph-Based SLAMを用いた軌跡推定シミュレーション」の5.3 最適化の手法のようなGraph-Based SLAMのアルゴリズムとほぼ一緒です。
Graph-Based SLAMとの違いはポーズ調整なので、ランドマーク(周辺環境に存在する特徴量となりうる物体)に対する拘束がなく位置姿勢間の拘束のみを考えます。
また、三次元なので状態量が増え、それに伴い誤差関数$\boldsymbol{e_{ij}=f(x_i,x_j)-d_{ij}}$とヤコビアン$\boldsymbol{\boldsymbol{J_{ij}=∂e_{ij}/∂x}}$の計算が大変になります。
位置姿勢表現
3次元におけるポーズ調整において2次元に比べ、大変なのはこの姿勢表現です。
ロボット等では、2次元では方位角を考えるだけで良いのですが、3次元の場合、姿勢のやりとりをクォータニオン$\boldsymbol{q}$で行います。
このクォータニオンを最適化のために回転ベクトル$\boldsymbol{\omega}$に変換します。
- クォータニオンから回転ベクトルの変換
$\boldsymbol{\omega(q)} = \frac{2\arccos(q_w)}{\sqrt{1-q_w^2}}[q_x \quad q_y \quad q_z]^T$
- 回転ベクトル$\boldsymbol{\omega(q)}$から回転行列$\boldsymbol{R}$への変換
$\boldsymbol{R} = \exp(\omega) = \Sigma_{n=0}^{\infty}\frac{K^n}{n!}$
ここで、$\boldsymbol{K(\omega)}$は以下です。
\boldsymbol{K(\omega)} = \frac{1}{\omega}
\begin{pmatrix}
0 & - \omega_z & \omega_y \\
\omega_z & 0 & \omega_x \\
- \omega_y & \omega_x & 0 \\
\end{pmatrix}
・・・なのですが、上の計算は重いので、実際はRodoriguesの公式より以下を用いて回転行列$R$を求めます。
$\boldsymbol{R} = \boldsymbol{I} + \sin(\omega) \boldsymbol{K(\omega)} +(1- \cos(\omega))\boldsymbol{K(\omega)}^2$
- 最適化する位置姿勢
上の姿勢表現をもとに最適化する位置姿勢は以下で表せられます。
$\boldsymbol{x_i=[p_i,\omega_i]}=[x_i,y_i,z_i,\omega_{xi},\omega_{yi},\omega_{zi}]$
ポーズ調整はこの位置姿勢からなる軌跡$\boldsymbol{x}$を求めます。
$\boldsymbol{x=[x_0,x_1,...]}$ - $\boldsymbol{x_i}$-$\boldsymbol{x_j}$間の相対位置姿勢
誤差関数を計算する際に$i,j$の位置姿勢から計算された相対位置姿勢$\boldsymbol{f(x_i,x_j)}$が必要なのですが、
$\boldsymbol{x_i}$-$\boldsymbol{x_j}$間の位置相対姿勢は以下で表されます、
相対位置:$\boldsymbol{K(\omega_j)^{T}(p_i - p_j)} $
相対姿勢:$\boldsymbol{\overline{q_j}\otimes q_i}$
ここで上線 (Overline)は共役であることを意味し、$\otimes$はクォータニオンの乗法演算子です。
アルゴリズム
アルゴリズム自体の導出は"graph-based SLAMの解説"や「Graph-Based SLAMを用いた軌跡推定シミュレーション」の5.3 最適化の手法を参照ください。
結論だけ書くと、以下の$\boldsymbol{\Delta x}$に関する線形方程式を解きます。
$\boldsymbol{\Delta x = -H^{-1}b}$
ここで、
$\boldsymbol{H=\Sigma H_{ij}=\Sigma J_{ij}^T\Omega_{ij} J_{ij}}$
$\boldsymbol{b = \Sigma b_{ij} =\Sigma e^T_{ij} \Omega_{ij} J_{ij}}$
です。(この$\boldsymbol{H}$と$\boldsymbol{b}$の構築が肝で"graph-based SLAMの解説"の3.4のように各エッジ毎に情報を追加していきます。)
上の線形方程式の解である$\Delta x$を使って軌跡$x$を更新します。
$\boldsymbol{x \gets x + \Delta x}$
これが1ステップになります。更新した軌跡$\boldsymbol{x}$を用いて、アルゴリズムを複数ステップ繰り返し、誤差関数の総和の変化が十分に小さくなった時の軌跡$\boldsymbol{x}$を最適解とします。
プログラム
プログラムは千葉工大fuRoのp2o: Single header 2D/3D graph-based SLAM library とAtsushiSakaiさんのPythonRobotics PoseOptimizationSLAM、"A graph optimization approach for motion estimation using inertial measurement unit data"のappendixを参考に書きました。
ソース置き場
書いたコードはGithubにあります。
Github rsasaki0109/PoseOptimizationSLAM3D

結果
データはグラフ最適化でよく使われるツールg2o(General Graph Optimization)のテストデータであるparking-garage.g2oを使いました。
青が最適化前の軌跡で、赤が最適化の軌跡です。
1回最適化した結果
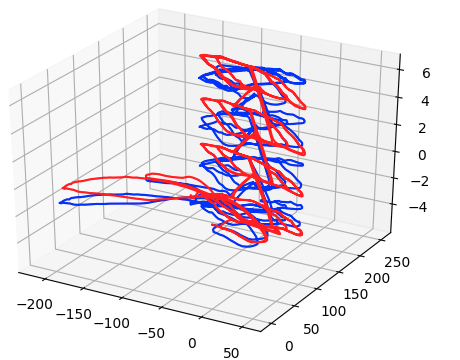
10回最適化した結果

標準出力におけるコストの遷移と1ステップにかかった時間
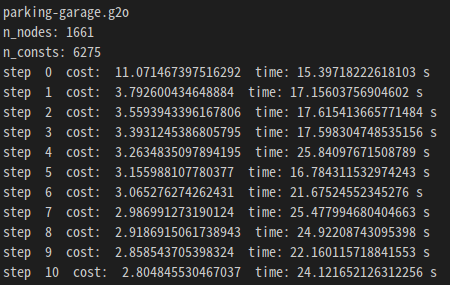
うまく最適化されていますね!pythonなのでC++と比べ、だいぶ時間がかかっています。
参考
友納正裕,"SLAM入門",2018
Grisetti G, Kummerle R, Stachniss C, Burgard W,"A tutorial on graph-
based slam",2010
上田隆一,"graph-based SLAMの解説"
金谷健一,"3次元回転: パラメータ計算とリー代数による最適化",2019
Rainer Kuemmerle, Giorgio Grisetti, Hauke Strasdat, Kurt Konolige, and Wolfram Burgard,"g2o: A General Framework for Graph Optimization", IEEE International Conference on Robotics and Automation (ICRA), 2011
Qiita クォータニオン (Quaternion) を総整理! ~ 三次元物体の回転と姿勢を鮮やかに扱う ~
Kiyoshi Irie,"A graph optimization approach for motion estimation using inertial measurement unit data",2018
入江 清,友納 正裕,"姿勢表現に回転ベクトルを用いた三次元グラフベースSLAM",2017