More than 5 years have passed since last update.

Graph-Based SLAMを用いた軌跡推定シミュレーション

Last updated at 2017-10-17Posted at 2017-09-12

1 はじめに

『確率ロボティクス』¹によると、SLAMは大きく分けてオンラインSLAMとオフラインSLAM２つの手法に分類される。
オンラインSLAMとは、各時刻において地図と姿勢の事後確率が計算される。

\begin{align}
    p(\ x_t,\ m\ |\ z_{1:t},\ u_{1:t}\ ) \tag{1.1}\\
\end{align}

式$(1.1)$を見ていただいてもわかるように、オンラインSLAMでは過去の観測、制御に対し、最新の姿勢$x_t$__だけ__を計算している。逐次最新の姿勢を計算するため、オンラインSLAMは__リアルタイム・アルゴリズム__である。
私が以前に作成した拡張カルマンフィルタ²やパーティクルフィルタ³による自己位置推定アルゴリズムはこのオンラインSLAMに該当する。

一方、オフラインSLAM（_完全SLAM__と言ったりもする）では、最新の姿勢$x_t$だけでなく、ロボットの軌跡全体$x{1:t}$に対して事後確率が計算される。

\begin{align}
    p(\ x_{1:t},\ m\ |\ z_{1:t},\ u_{1:t}\ ) \tag{1.2}\\
\end{align}

オフラインSLAMは特定のタイミングで計算が実行されるため、__バッチ・アルゴリズム__となる。

2 Graph-Based SLAM

最近のSLAMの主流はグラフを用いたオフラインSLAMであり、グラフを用いたオフラインSLAMのことを一般的に__Graph-Based SLAM__という⁴。
今回はこのGraph-Based SLAMをPythonで実装し、その動作を確認していきたいと思う。
なお、実装の際に参考にした論文は"A Tutorial on Graph-based SLAM⁵"と"graph-based SLAMの解説⁶"となります。

3 ロボットの姿勢と動作モデル

ロボットの姿勢と動作モデルは書籍『確率ロボティクス』¹の「5章ロボットの動作」を適用するので、詳細は書籍を参考にしてほしい。
よって、ここでは簡単に説明をする。
まず、ある離散的な時刻$t$におけるロボットの姿勢$\boldsymbol{x}$を以下のように定義する。

\begin{align}
    \boldsymbol{x}_{t} =
       \begin{bmatrix}
        x_{t} \\
        y_{t} \\
        \theta_{t} \\
       \end{bmatrix} \tag{3.1}\\
\end{align}

時刻$t$において、ロボットは__並進速度$v_{t}$_と__回転速度$\omega{t}$を与えられ、時刻$t'$に姿勢$\boldsymbol x{t'}$が得られるものとする。しかし、実環境では__並進速度$v{t}$_と__回転速度$\omega{t}$__には雑音が乗るため、以下のような式で表すことができる。

\begin{align}
    \begin{bmatrix}
        x_{t'} \\
        y_{t'} \\
        \theta_{t'} \\
    \end{bmatrix}
    = 
    \begin{bmatrix}
        x_{t} \\
        y_{t} \\
        \theta_{t} \\
    \end{bmatrix}
    +
    \begin{bmatrix}
        -\frac{v_{t}}{\omega_{t}}sin\theta_{t}
           + \frac{v_{t}}{\omega_{t}}sin(\theta_{t}+\omega_{t}\Delta t) \\
        \frac{v_{t}}{\omega_{t}}cos\theta_{t}
           - \frac{v_{t}}{\omega_{t}}cos(\theta_{t}+\omega_{t}\Delta t) \\        
        \omega_{t}\Delta t + \gamma_{t}\Delta t \\
    \end{bmatrix}

    \tag{3.2}\\
\end{align}

但し、

\begin{align}
    \begin{bmatrix}
        v_{t} \\
        \omega_{t} \\
        \gamma_{t} \\
    \end{bmatrix}
    = 
    \begin{bmatrix}
        v^\ast_{t} \\
        \omega^\ast_{t} \\
        0 \\
    \end{bmatrix}
    +
    \begin{bmatrix}
        \varepsilon_{\alpha_1 {v_{t}^\ast}^2 + {\alpha_2 \omega_{t}^\ast}^2} \\
        \varepsilon_{\alpha_3 {v_{t}^\ast}^2 + {\alpha_4 \omega_{t}^\ast}^2} \\
        \varepsilon_{\alpha_5 {v_{t}^\ast}^2 + {\alpha_6 \omega_{t}^\ast}^2} \\
    \end{bmatrix}

    \tag{3.3}\\
\end{align}

である。ここで、$v_{t}^\ast$、$\omega_{t}^\ast$はそれぞれ、並進速度、回転速度の真値を表す。また、$\varepsilon$は雑音を表し、$\alpha_1$から$\alpha_6$はロボット固有の雑音パラメータである。ここで、$\varepsilon_b$は平均がゼロで標準偏差が$b$の誤差変数を意味する。

3.1 座標系の定義

Graph-Based SLAMを実装するにあたり、以下３つの座標系を定義する。

世界座標系

世界のある1点を基準とした座標系。静止したランドマークは基本的に世界座標系では移動しない。

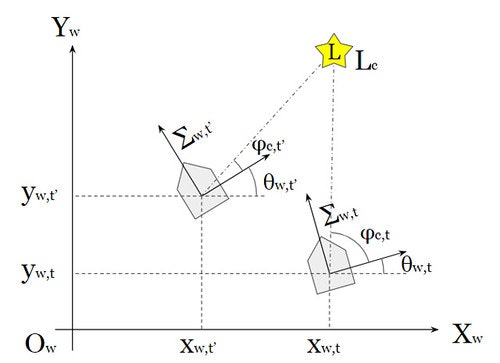
ロボット座標系

ロボット上のある1点を基準とした座標系。基準点はロボットと共に移動していく。よって、静止したランドマークはロボットの移動に伴い、移動していくことになる。
また、ランドマークは基本的にこのロボット座標系で観測される。

4 ランドマークの観測モデル

ランドマークの観測モデルは"graph-based SLAMの解説⁶"の「2.2 観測」を適用するのでそちらを参考にしてほしい。よって、ここでは簡単に説明する。
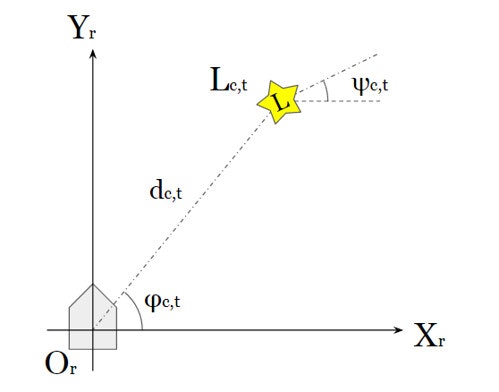
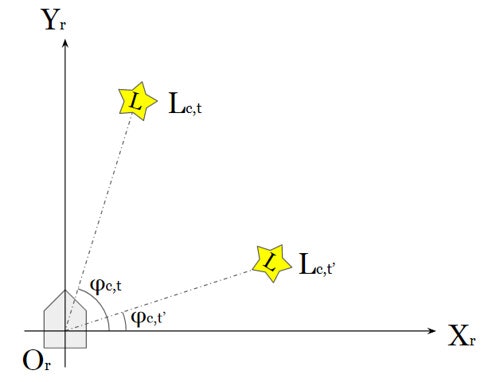
ある離散的な時刻$t$に、ロボット座標系にてランドマーク$L_c$を観測すると、以下3つのランドマークに関する情報が得られるものとする。

ランドマーク$L_c$までの距離：$d_{c,t}$
ランドマーク$L_c$が観測された方角：$\varphi_{c,t}$
ランドマーク$L_c$自身が向いている方角：$\psi_{c,t}$

式で表すと以下のようになる。

\begin{align}
    \begin{bmatrix}
        d_{c,t} \\
        \varphi_{c,t} \\
        \psi_{c,t} \\
    \end{bmatrix}
    = 
    \begin{bmatrix}
        d^\ast_{c,t} \\
        \varphi^\ast_{c,t} \\
        \psi^\ast_{c,t} \\
    \end{bmatrix}
    +
    \begin{bmatrix}
        \varepsilon_{\beta_1 {d^\ast_{c,t}}^2} \\
        \varepsilon_{\beta_2} \\
        \varepsilon_{\beta_3} \\
    \end{bmatrix}

    \tag{4.1}\\
\end{align}

$d^\ast_{c,t}$、$\varphi^\ast_{c,t}$、$\psi^\ast_{c,t}$、はそれぞれ真値を表し、$\beta_1$から$\beta_3$はロボット固有の雑音パラメータである。

5 Graph-Based SLAM 問題

5.1 ロボットの相対姿勢計算

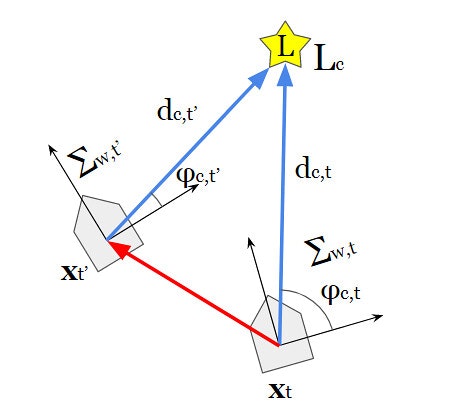
問題を解くために、ノード（頂点）とエッジ（辺）を持つグラフを考える。ノードはロボットの各時刻の姿勢に対応しており、エッジは同一のランドマークを観測した２つのノード間に設定される。

このとき、各時刻のロボットの相対姿勢を算出する方法は以下の２通り存在することがわかる。

①各時刻でのノード間における、ロボット推定姿勢の差：$ \Delta \boldsymbol x_{t,t'}$

これは単純に姿勢差を計算すればよい。

\begin{align}
    \Delta \boldsymbol{x}_{t,t'} = \boldsymbol{x}_{t'} - \boldsymbol{x}_t
    \tag{5.1}\\
\end{align}

②同一ランドマークを観測した各時刻での観測ベクトル：$ \Delta \boldsymbol x^{L}_{c,t,t'}$

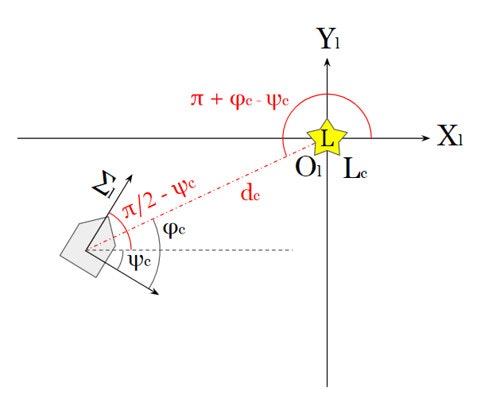
ランドマークを観測した際、観測結果を元にランドマークを基準とした座標系に変換した結果を下図に示す。

この図より、ランドマークを基準としたロボットの相対姿勢$\boldsymbol x^L_{c}$は以下の式で表される。

\begin{align}
    \boldsymbol{x}^L_{c}
    = 
    \begin{bmatrix}
        x^L_{c} \\
        y^L_{c} \\
        \theta^L_{c} \\
    \end{bmatrix}
    = 
    \begin{bmatrix}
        d_{c} \, cos \left( \pi + \varphi_{c} - \psi_{c} \right) \\
        d_{c} \, sin \left( \pi + \varphi_{c} - \psi_{c} \right) \\
        \frac{\pi}{2} - \psi_{c} \\
    \end{bmatrix}

    \tag{5.2}\\
\end{align}

これを、時刻$t$及び、$t'$について計算し、差を求める。

\begin{align}
    \Delta \boldsymbol{x}^{L}_{c,t,t'} = \boldsymbol{x}^L_{c,t'} - \boldsymbol{x}^L_{c,t}
    \tag{5.3}\\
\end{align}

ここで、$\Delta \boldsymbol x_{t,t'}$と$\Delta \boldsymbol x^L_{c,t,t'}$の差を考える。

\begin{align}
    \boldsymbol{e}_{c,t,t'} = \Delta \boldsymbol{x}_{t,t'} - \Delta \boldsymbol{x}^L_{c,t,t'}   \tag{5.4}\\
\end{align}

この誤差$\boldsymbol e_{c,t,t'}$がゼロとなるときの$\Delta \boldsymbol x_{t,t'}$つまり、$\boldsymbol x_{t}$と$\boldsymbol x_{t'}$が最適な推定姿勢であると言える。
しかし、各エッジには誤差が含まれていることと、各ノードは他のエッジとも紐付いているため、全ての誤差$\boldsymbol e_{c,t,t'}$がゼロになることはまず有りえない。
よって、全ての誤差$\boldsymbol e_{c,t,t'}$が最適と言える推定姿勢の計算方法を考える必要がある。

5.2 情報行列の計算

情報行列の計算モデルも"graph-based SLAMの解説⁶"の「3.1.2 $\Sigma_{c,t,t'}, \Omega_{c,t,t'}$の計算」を適用するのでそちらを参考にしてほしい。よって、ここでは簡単に説明する。

\begin{align}
    \boldsymbol{\Sigma}_{c,t}
    = 
    \begin{bmatrix}
        \left(\beta_1 d^\ast_{c,t}\right)^2 & 0 & 0 \\
        0 & \left(d^\ast_{c,t} \ sin \beta_2\right)^2 & 0 \\
        0 & 0 & {\beta_2}^2 + {\beta_3}^2 \\
    \end{bmatrix}

    \tag{5.5}\\
\end{align}

次に、計測座標系で計算した$\boldsymbol \Sigma_{c,t}$ と$\boldsymbol \Sigma_{c,t'}$を世界座標系に変換する。
変換には以下の回転行列を用いる。

\begin{align}
    \boldsymbol{R}_{c,t}
    = 
    \begin{bmatrix}
        c & -s & 0 \\
        s & c & 0 \\
        0 & 0 & 1 \\
    \end{bmatrix}

    \tag{5.6}\\
\end{align}

但し、

\begin{align}
    c = cos(\theta_t + \varphi_t)       \tag{5.7}\\
    s = sin(\theta_t + \varphi_t)       \tag{5.8}\\
\end{align}

である。

※参考文献の"graph-based SLAMの解説⁶"の式$(10)$と"s"の符号が異なっている。私は半時計回りの方向を正としているが、参考文献は時計回りの方向を正としたのだろうか？

最終的に世界座標系における、共分散行列$\boldsymbol \Sigma_{c,t,t'}$と情報行列$\boldsymbol \Omega_{c,t,t'}$は以下となる。

\begin{align}
    \boldsymbol{\Sigma}_{c,t,t'} &= \boldsymbol{R}_{c,t}\,\boldsymbol{\Sigma}_{c,t}\,\boldsymbol{R}_{c,t}^T
                     + \boldsymbol{R}_{c,t'}\,\boldsymbol{\Sigma}_{c,t'}\,\boldsymbol{R}_{c,t'}^T   \tag{5.9}\\
    \boldsymbol{\Omega}_{c,t,t'} &= \boldsymbol{\Sigma}_{c,t,t'}^{-1}    \tag{5.10}\\
\end{align}

5.3 最適化の手法

いよいよ本題の肝となる最適化問題である。まず、ロボットが各時刻に得られた観測結果のエッジ２つ１組のペアを全通り作成する。この全ペアの集合を$\mathcal{C}$とし、２乗誤差の和を求める評価関数を定義する。

\begin{align}
    \boldsymbol{F}(\boldsymbol{x}) = \displaystyle \sum_{ \boldsymbol{e}_{c,t,t'} 
       \in \mathcal{C} }^{  } \ \underbrace{\boldsymbol{e}_{c,t,t'}^T \, \boldsymbol{\Omega}_{c,t,t'} \, \boldsymbol{e}_{c,t,t'}}_{\boldsymbol{F}_{t,t'}}   \tag{5.11}\\
\end{align}

この上式の$\boldsymbol{F}(\boldsymbol{x})$が最小となる$\hat{\boldsymbol{x}}$を求めることが最終的な目的である。

最小値$\hat{\boldsymbol{x}}$を求めるアプローチ方法としてはGauss-Newton法やLevenberg-Marquardt法を用いるのが一般的とのこと。
Gauss-Newton法やLevenberg-Marquardt法については以下のサイトが参考になると思いますので、興味あったら覗いてみてください。

CVIM#11 3. 最小化のための数値計算

今回は"A Tutorial on Graph-based SLAM⁵"と同じようにGauss-Newton法で解いていきます。

まず始めに、$\boldsymbol F_{c,t,t'}$と$\boldsymbol x_{t'}$をそれぞれ、$\Delta\boldsymbol x_{t}$、$\Delta\boldsymbol x_{t'}$変化させた場合を考える。
式で表すと、

\begin{align}
    \boldsymbol{e}_{c}(\boldsymbol{x}_{t} + \Delta\boldsymbol{x}_{t},\,\boldsymbol{x}_{t'} + \Delta\boldsymbol{x}_{t'}) 
      \ &=\ \boldsymbol{e}_{c}(\boldsymbol{x}_{t,t'}+\Delta\boldsymbol{x}) \tag{5.12}\\
      \ &\simeq\ \boldsymbol{e}_{c,t,t'} + 
         \left.\frac{\partial \boldsymbol{e}_{c,t,t'}}
                    {\partial \boldsymbol{x}}
         \right|_{\boldsymbol{x}=\boldsymbol{x}_{t,t'}}\Delta\boldsymbol{x}
   \tag{5.13}
\end{align}

と表される。但し、ヤコビ行列は$\boldsymbol{J}_c$を使って

\boldsymbol{J}_{c,t,t'} = \left.\frac{\partial \boldsymbol{e}_{c,t,t'}}{\partial\boldsymbol{x}}\right|_{\boldsymbol{x}=\boldsymbol{x}_{t,t'}}   \tag{5.14}

と表される。よって、

\begin{align}
    \boldsymbol{F}(\boldsymbol{x}+\Delta\boldsymbol{x}) &= \sum_{ \boldsymbol{e}_{c,t,t'} \in \mathcal{C} } \boldsymbol{F}(\boldsymbol{x}_{t,t'}+\Delta\boldsymbol{x})   \tag{5.15}\\
   &\simeq \sum_{ \boldsymbol{e}_{c,t,t'} \in \mathcal{C} } \ 
      (\boldsymbol{e}_{c,t,t'} + \boldsymbol{J}_{c,t,t'}\Delta{\boldsymbol{x}} )^T
      \, \boldsymbol{\Omega}_{c,t,t'} \,
      (\boldsymbol{e}_{c,t,t'} + \boldsymbol{J}_{c,t,t'}\Delta{\boldsymbol{x}} )   \tag{5.16}\\
   &= \sum_{ \boldsymbol{e}_{c,t,t'} \in \mathcal{C} } \ 
      \underbrace{\boldsymbol{e}_{c,t,t'}^T \boldsymbol{\Omega}_{c,t,t'} \boldsymbol{e}_{c,t,t'}}_{c_{c,t,t'}}
     + 2 \, \underbrace{\boldsymbol{e}_{c,t,t'}^T \boldsymbol{\Omega}_{c,t,t'} \boldsymbol{J}_{c,t,t'}}_{\boldsymbol{b}_{c,t,t'}} \Delta{\boldsymbol{x}} + \Delta{\boldsymbol{x}}^T \underbrace{\boldsymbol{J}_{c,t,t'}^T \boldsymbol{\Omega}_{c,t,t'} \boldsymbol{J}_{c,t,t'}}_{\boldsymbol{H}_{c,t,t'}}\Delta{\boldsymbol{x}}   \tag{5.17}\\

   &= \sum_{ \boldsymbol{e}_{c,t,t'} \in \mathcal{C} } \ 
      c_{c,t,t'} + 2 \, \boldsymbol{b}_{c,t,t'} \Delta{\boldsymbol{x}}
     + \Delta{\boldsymbol{x}}^T \boldsymbol{H}_{c,t,t'}\Delta{\boldsymbol{x}}   \tag{5.18}\\

   &= \underbrace{\sum_{ \boldsymbol{e}_{c,t,t'} \in \mathcal{C} } c_{c,t,t'}}_{\boldsymbol{c}}
     + 2 \underbrace{\left(\sum_{ \boldsymbol{e}_{c,t,t'} \in \mathcal{C} } \, \boldsymbol{b}_{c,t,t'} \right)}_{\boldsymbol{b}} \Delta{\boldsymbol{x}} 
     + \Delta{\boldsymbol{x}}^T \underbrace{\left( \sum_{ \boldsymbol{e}_{c,t,t'} \in \mathcal{C} }  \boldsymbol{H}_{c,t,t'} \right)}_{\boldsymbol{H}} \Delta{\boldsymbol{x}}   \tag{5.19}\\

   &= \boldsymbol{c}
    + 2 \boldsymbol{b} \Delta{\boldsymbol{x}}
    + \Delta{\boldsymbol{x}}^T \boldsymbol{H} \Delta{\boldsymbol{x}}   \tag{5.20}\\
\end{align}

式$(5.20)$の$\boldsymbol{c}$は定数となる。さらに、式$(5.20)$の変曲点を計算すると、

\begin{align}
   2 \boldsymbol{b} + 2 \boldsymbol{H} \Delta{\boldsymbol{x}} = 0   \tag{5.21}\\
\end{align}

よって、$\Delta \boldsymbol{x}$は

\begin{align}
   \Delta{\boldsymbol{x}} = -\boldsymbol{H}^{-1} \boldsymbol{b}   \tag{5.22}\\
\end{align}

となる。
計算された$\Delta \boldsymbol{x}$を使って$\boldsymbol{x}$を更新する。

\begin{align}
   \boldsymbol{x} \leftarrow \boldsymbol{x}＋\Delta \boldsymbol{x}   \tag{5.23}\\
\end{align}

更新した$\boldsymbol{x}$を使って式$(5.11)$の$\boldsymbol{F}(\boldsymbol{x})$を計算し、計算結果が十分小さくなるまで式$(5.12)$からの計算を繰り返す。
計算結果が十分小さいときの$\boldsymbol{x}$を最適解$\hat{\boldsymbol{x}}$とする。

6 実装

Graph-Based SLAMをPythonで実装してみました。
スクリプトはGitHubで公開しています。
・GitHub - graph_based_slam.py

スクリプトを実行した結果は以下のようになります。
（画像をクリックするとYouTubeへジャンプします。）

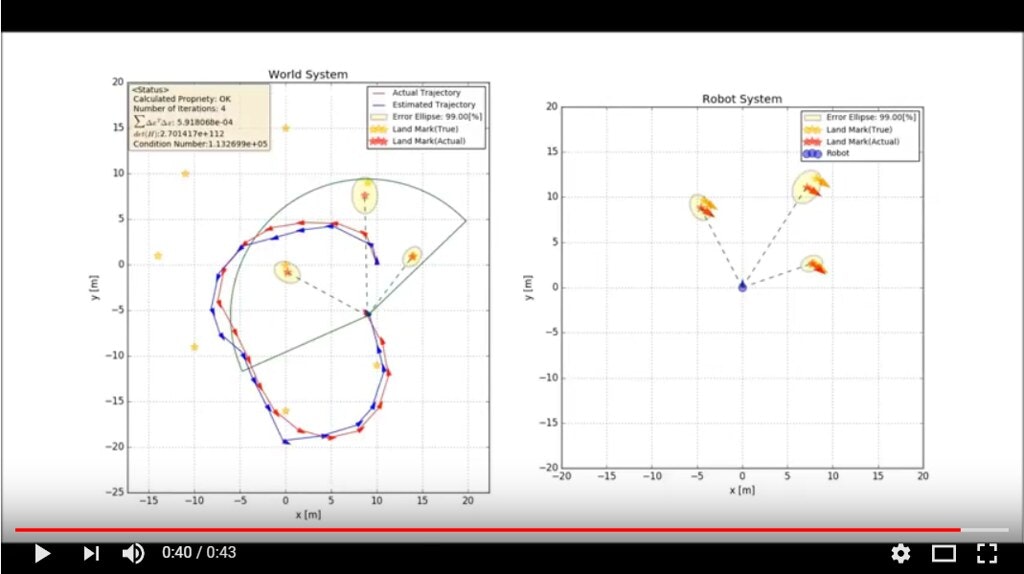
※詳しい説明は後々追加していこうと思います。

7 さいごに

最近流行のGraph-Based SLAMを実装してみましたが、正直実装もこの記事書くのもしんどかったです。
上手く動かないこともありましたが、なんとか意図した通りに動かすことができてよかったです。
まだまだ内容の薄い記事ですが、一旦ここで公開しようと思います。
説明不足の個所も多々あると思いますが、指摘していただければ追記していこうと思います。
また、実装するに当たり、上田さんの解説が大変参考になりました。

"graph-based SLAMの解説⁶"

次は実機でSLAMを動かしていきたいと思います♪

参考文献

"確率ロボティクス (プレミアムブックス版)", マイナビ出版, 2005. ↩ ↩²
拡張カルマンフィルタによる自己位置推定動作の可視化 ↩
パーティクルフィルタによる自己位置推定動作の可視化 ↩
友納正裕：移動ロボットの環境認識 —地図構築と自己位置推定 ↩
G. Grisetti, R. Kummerle, C. Stachniss, and W. Burgard. A Tutorial on Graph-based SLAM. IEEE Trans. on Intelligent Transportation Systems Magazine, 2:31–43, 2010. ↩ ↩²
上田隆一：graph-based SLAMの解説 ↩ ↩² ↩³ ↩⁴ ↩⁵

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up