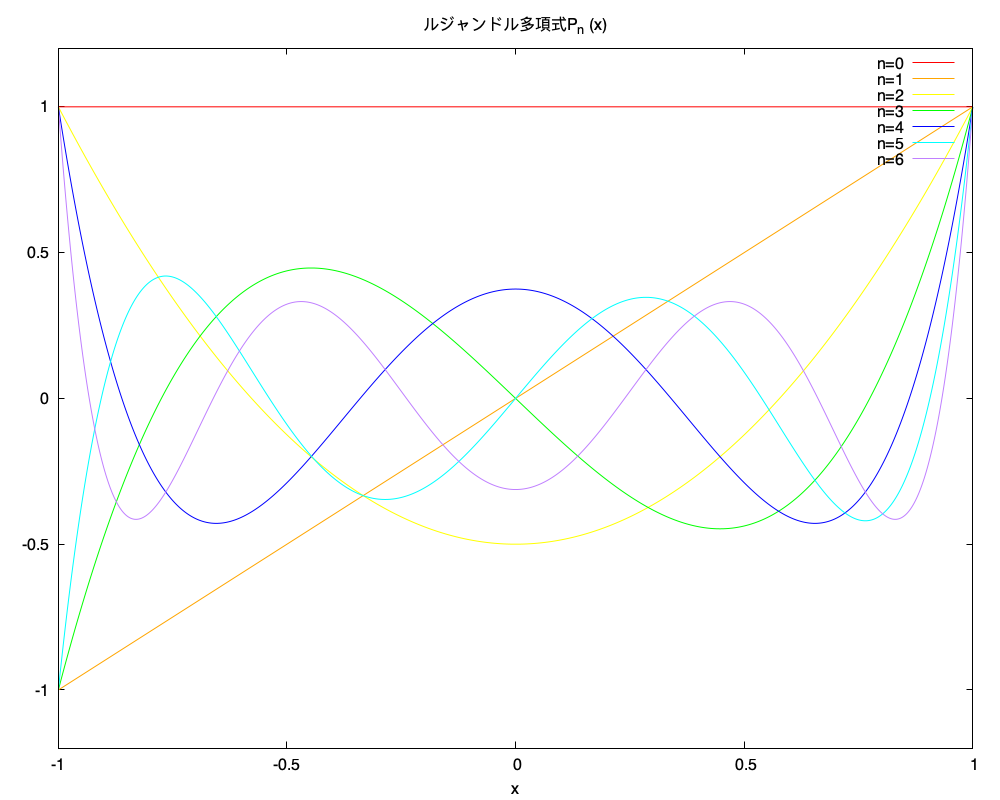
ルジャンドル多項式(Fortran)

　ルジャンドル多項式を使う場面があったので、ついでにFORTRAN上で関数を実装した。ということで備忘録をば。

　ちなみに、計算には一般項
$$
P_n(x) = \displaystyle\sum_{r=0}^{\left[\frac{n}{2}\right]}\dfrac{(-1)^r (2n-2r)!}{2^n r!(n-r)!(n-2r)!}x^{n-2r}
$$

を用いている。

legendre

real(8) function legendre(n,x)
    implicit none
    integer , intent(in) :: n
    real(8) , intent(in) :: x
    real(8) :: temp
    integer :: r,i,minus1expr

    temp=0.0
    minus1expr = -1.0

    do r = 0,floor(real(n,8)/2.0)
        
        if(mod(r,2)==0)then
            minus1expr = 1
        else
            minus1expr = -1
        end if

        temp = temp + (minus1expr*factorial(2*n-2*r)/&
        & ((2.0**real(n,8))*factorial(r)*factorial(n-r)*factorial(n-2*r)))*&
        & (x**real(n-2*r,8))

    end do

    legendre = temp
    return

end function legendre

ちなみに、factorialは下のように計算している。integerでやるとあっさりオーバーフローするので、実数で計算してるンゴ。

factorial

real(8) function factorial(n)
    implicit none
    integer,intent(in):: n
    integer ::i
    real(8) :: temp

    temp=1
    if (n==0) then
        temp=1.0
    else
        do i = 1,n
            temp = temp*real(i,8)
        end do
    end if

    factorial = temp
    return
     
end function factorial

図

まあ、いい感じなんでね。