Tensorflowで粒子の動力学シミュレーション

お断り

Tensorflowについて

当記事は機械学習による物理モデルの学習ではありません。粒子の力学シミュレーションに必要な数式を愚直にTensorflowで書いてみたものになります。

なお、tensorflow2はまだ対応していません。

シンプレクティック法について

僕は分子動力学法について、物理からというよりかは化学から入りましたので、厳密な議論ができていないかもしれません。動かしてみて結果が妥当なら何か言えるだろう、くらいのスタンスです。

環境

• Tensorflow1.10くらい
• python3

数学

解析力学の正準方程式を思い出します。 $H$をハミルトニアン（保存量）、$\vec{q}$を位置、$\vec{p}$を共役の運動量としますと、$\vec{p}$と$\vec{q}$の$i$番目の成分の時間発展は以下のようになります。

\dot{q}_i = \frac{\partial H}{\partial p_i}\\
\dot{p}_i = - \frac{\partial H}{\partial q_i}

あるいは、$\vec{z} = (\vec{q}, \vec{p})$と書いて

\dot{\vec{z}} = \left(\frac{\partial H}{\partial \vec{p}}\frac{\partial}{\partial\vec{q}} - \frac{\partial H}{\partial \vec{q}}\frac{\partial}{\partial\vec{p}} \right)\vec{z} = (\hat{T} + \hat{U})\vec{z}\tag{1}

とできます。ここで$\hat{T}$, $\hat{U}$は

\hat{T} = \frac{\partial H}{\partial \vec{p}}\frac{\partial}{\partial\vec{q}}\\
\hat{U} =  - \frac{\partial H}{\partial \vec{q}}\frac{\partial}{\partial\vec{p}} 

の部分の項で、それぞれ運動エネルギー、位置エネルギーに対応するとします。
あ、今回の話はハミルトニアンが$H = T(p) + U(q)$というように、位置だけに依存する関数と運動量だけに依存する関数の別々の関数の和で表現できるというのが条件ですが、普通にポテンシャルが定義できて摩擦など余計なものが無い系ならこの条件を満たします。

　さて、天下り的ですが、$\hat{T}$, $\hat{U}$はexponentialの肩に載せ、$p$や$q$に作用させると時間を進めることができます。ここでは$\tau$だけ進めるとしますと、

\vec{q}(t+\tau) = e^{\tau\hat{T}} \vec{q}(t) = \vec{q}(t) + \tau\frac{\partial H}{\partial \vec{p}} \\
\vec{p}(t+\tau) = e^{\tau\hat{U}} \vec{p}(t) = \vec{p}(t) - \tau\frac{\partial H}{\partial \vec{q}}

と書くことができます。$\exp()$をテイラー展開すれば確かめることができます。
運動エネルギー$T = p^2/(2m) $は$\partial T/\partial q = 0$, ポテンシャル$U$は$\partial U / \partial p = 0 $となりますので、$\hat{T}\hat{T}\vec{q} = \hat{U}\hat{U}\vec{p} = 0$となると思います。

こうすると

\dot{\vec{z}} = (\hat{T} + \hat{U})\vec{z}\tag{1}

の形式解は

\vec{z}(t) = e^{t(\hat{T} + \hat{U})}\vec{z}(0)

とできます。ここで、$e^{t(\hat{T} + \hat{U})}$を何らかプログラムの形で書き下せるなら、世の分子動力学シミュレーションはこんな苦労はしていません。つまり、$e^{\tau(\hat{T} + \hat{U})}$ の具体的な表現は神の味噌汁。これは$\hat{T}$, $\hat{U}$が可換ではないことに拠ります。このため、

e^{\tau(\hat{T} + \hat{U})}

を

e^{\tau\hat{T}}, e^{\tau\hat{U}}

で分解していくことになります。

時間ステップ

まず分解の前に下処理。さっきからちらほら出ている$\tau$ですが、これは目的の時刻$t$までを$N$ステップで刻むとして$\tau = t/N$とおき、

e^{t(\hat{T} + \hat{U})} = \prod^N e^{\tau(\hat{T} + \hat{U})}

としています。$e^{\tau(\hat{T} + \hat{U})}$を分解するときの誤差は$\tau$に依存するので、これを小さくする処理になります。

トロッター分解

参考：https://qiita.com/kaityo256/items/b7e0568cad8b86c5c8ea

導出は省きます。

１次

e^{\tau(\hat{T} + \hat{U})}  \approx e^{\tau\hat{T}}e^{\tau\hat{U}} \ または\ e^{\tau\hat{U}}e^{\tau\hat{T}}

2次

e^{\tau(\hat{T} + \hat{U})} \approx e^{\frac{\tau}{2}\hat{T}}e^{\tau\hat{U}}e^{\frac{\tau}{2}\hat{T}} \ または\ e^{\frac{\tau}{2}\hat{U}}e^{\tau\hat{T}}e^{\frac{\tau}{2}\hat{U}}

なお、普通のニュートン力学での２次はVerlet法に式変形できます。

４次以上の偶数次

$\mathrm{symp2d}(x)$を時間$x$だけ進める２次の時間発展演算子としますと、次数ごとに一定の規則で決まる係数列$d_i$を使って

e^{\tau(\hat{T} + \hat{U})} \approx \prod_i \mathrm{symp2d}(d_i\tau)

と高次の展開を２次の展開の積で書けるという定理があります。例えば、４次では

d_1 = \frac{1}{2- \sqrt[3]{2}}\\
d_2 = - \frac{\sqrt[3]{2}}{2 - \sqrt[3]{2}}\\
d_3 = d_1

と３回の２次展開した演算子の積で書くことができます。

　普通のMDでは

\hat{T} = \frac{\partial H}{\partial \vec{p}}\frac{\partial}{\partial\vec{q}} = \frac{\vec{p}}{m}\frac{\partial}{\partial\vec{q}}\\
\hat{U} =  - \frac{\partial H}{\partial \vec{q}}\frac{\partial}{\partial\vec{p}} =  - \frac{\partial U(\vec{q})}{\partial \vec{q}}\frac{\partial}{\partial\vec{p}}

となります。ポテンシャル $U(\vec{q})$ は分子間力など計算がややこしいのが多いので、普通の系では $\partial U(\vec{q})/\partial \vec{q}$ が含まれる $\exp(\tau\hat{U})$ が計算時間がかかる項になります。なので、これを出来るだけ少ない回数適用するアルゴリズムにします。

１次の積分は

\vec{q}(t + \tau) = \tau\vec{p}(t) + \vec{q}(t)\\
\vec{p}(t + \tau) = \tau\vec{F}(t + \tau) + \vec{p}(t)

ここで

 \vec{F}(t) = - \frac{\partial U(\vec{q}(t))}{\partial \vec{q}}

は力です。
2次は

\vec{q}(t + \frac{\tau}{2}) =  \frac{\tau}{2}\vec{p}(t) + \vec{q}(t)\\
\vec{p}(t + \tau) = \tau\vec{F}(t +  \frac{\tau}{2}) + \vec{p}(t)\\
\vec{q}(t + \tau) =  \frac{\tau}{2}\vec{p}(t + \tau) + \vec{q}(t +  \frac{\tau}{2})

として、 $\vec{F}$ の計算が1回だけになる順番にします。

１粒子

まず、Tensorflowで数値積分を書くことに集中するため、物理的にはとにかく簡単な系にします。ここでは２次元平面中の原点に万有引力で引かれる質点を考えます。

モジュール

tensorflowを以下のようにインポートします。numpyはあると便利なのでついでにインポートしておきます。

import tensorflow as tf
import numpy as np

定数の定義

G = 1.0 # 万有引力定数
m = 1.0 # 質点の質量
Mc = 1.0 # 原点の質量
Mm = Mc*m # 万有引力の質量の項

変数の定義

fp = tf.float64
r = tf.get_variable("position", shape=[2], dtype=fp)
p = tf.get_variable("momentum", shape=[2], dtype=fp)

ともに２次元のベクトルです。
fpは浮動小数点の精度です。今回は特にGPUとか使いませんので、単精度以上であれば問題ないです。

位置エネルギー

U = -G\frac{Mn}{\sqrt{\vec{r}^2}}

rr = tf.rsqrt(tf.reduce_sum(r**2))
U = - G*Mm*rr

運動エネルギー

T = \frac{\vec{p}^2}{2m}

pr2 = tf.reduce_sum(p**2)
T = 0.5*pr2/m

ハミルトニアン

H = U + T

H = U + T

これでハミルトニアンまでの計算グラフが定義できました。

力と速度

\vec{F} = - \frac{\partial H}{\partial \vec{r}}, \vec{v} = \frac{\partial H}{\partial \vec{p}}

F = - tf.gradients(H, r)[0]
v = tf.gradients(H, p)[0]

tf.gradientsの第２引数はタプルにでき、そのときのために返り値がタプル形式となっています。そのため、[0]がついています。

また、vは極端な話がただの速度なので、

v = p/m

でも問題ないです。

座標更新演算子

e^{Tdt}: \vec{r} \leftarrow \vec{r} + \vec{v}dt\\
e^{Udt}: \vec{p} \leftarrow \vec{p} + \vec{F}dt

dt = tf.placeholder(fp)
expT = tf.assign_add(r, dt*v)
expU = tf.assign_add(p, dt*F)

これでMDに必要な計算グラフは一通り定義できました。

初期値代入演算

rとpはプレースホルダーではない変数なので、初期化する操作が必要になります。適切なinitializerでも初期化できますが、セッション中に外部から好きな変数（つまりこちらの都合で決めた初期値）を入れられるプレースホルダーからアサインする方法を採用します。

r0 = tf.placeholder(fp, shape=[2])
p0 = tf.placeholder(fp, shape=[2])
init_assign = [tf.assign(r, r0), tf.assign(p, p0)]

ここまでのプログラムは計算グラフの設計のためのコードになりますので、実際の計算はしていません。これからセッションなるものを用意して、実際のテンソルを流し込んで計算グラフを評価してやることで、ほしい値を得たり定義した操作をしたりします。

セッション自体の初期化

いよいよ位置などの変数を初期化します。

initializer = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(initializer)
    sess.run(init_assign, feed_dict={r0: np.array([1.0, 0.0]), p0: np.array([0.0, 1.0])})
    while True:
        ここからMD時間発展

とりあえず、$(x, y) = (1, 0)$ の点に、$y$ 軸方向に速度 1 で飛んでいる粒子を用意しました。

MD本体

以下、while Trueの中のブロックになります。

            # 時間発展部分
            sess.run(expT, feed_dict={dt: 0.1})
            sess.run(expU, feed_dict={dt: 0.1})
            # 計算経過確認のための出力
            r_t = sess.run(r)
            U_t = sess.run(U)

これで1次のシンプレクティック法が完成しました。
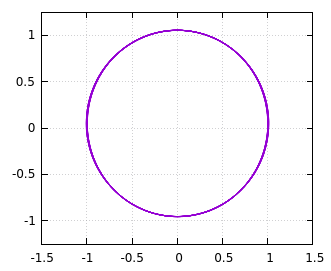
毎回計算したr_tを適当なファイルに保存するなり、リストに蓄えてmatplotlibに渡すなりして軌跡を可視化すると以下のようになります。

この線の部分を拡大すると以下のようになります。

陽的オイラー法

ここで、tensorflowの sess.run は複数のノードを指定できます。つまり、以下のように書けるのでは、と思った人もいるでしょう。

            # 時間発展部分
            sess.run((expT, expU), feed_dict={dt: 0.1})

ちなみにこのときsess.runの戻り値は第一引数のタプルに対応した長さのタプルになります。

これで時間発展を行いますと、以下のような軌跡になります。

明らかに保存していません。どうも sess.run((expT, expU), feed_dict={dt: 0.2})とまとめると、expTとexpUの計算グラフでは位置rと運動量pが共通になりますので、tensorflowは渡されたタプルについて同じ $r(t)$、$p(t)$で計算してしまうようです。つまり、差分の計算が

\vec{r}(t+\tau) = \tau\vec{v}(t) + \vec{r}(t)\\
\vec{p}(t+\tau) = \tau\vec{F}(t) + \vec{p}(t)

となってしまいます。これはオイラー法に対応します。一方、正しいシンプレクティック法では、

\vec{r}(t+\tau) = \tau\vec{v}(t) + \vec{r}(t)\\
\vec{p}(t+\tau) = \tau\vec{F}(t + \tau) + \vec{p}(t)

と演算子を作用させる位置・運動量の時刻が異なります。このため、

            # 時間発展部分
            sess.run(expT, feed_dict={dt: 0.2})
            sess.run(expU, feed_dict={dt: 0.2})

として２回のsess.runに分解して、１回の時間発展で２回の変数の更新を別々に行っていたのでした。

多粒子系

さて、多粒子系にすると、２体間の相互作用で座標の差を取り出すという¹ちょっとむずかしい問題が出てきます。
普通のプログラム（といいつつFortranによる擬似コードですが）では

do i = 1, N-1
   do j = i+1, N
       r = distant_of(x(:, i), x(:, j))
       U = U + interaction(r)
   enddo
enddo

とループで書けます。一方でtensorflowでは、座標を

x = tf.Variable(shape=[None, 3])

として持った時、先ほどのFortranの例のように

for i in range(N-1):
   for j in range(i+1, N):
       dxij = x[i, :] - x[j, :]
       # 以下略

とループにした時、以下のような問題が考えられます。

• 添字を切り出すループはNumpyではご法度レベルのパフォーマンス低下。Tensorflowでもpython側のループにより計算グラフが細切れになり、やっぱりパフォーマンス低下が起こります。
• 何らかの理由でループ対象粒子数Nを動的に変える必要があったとき、グラフを事前に作るこの方法では対応できません。

Tensorflowでテンソルの添字にわたって関数を適用するfoldとかmapとかがあり、うまく使えばこれらの問題は解決できるかもしれませんが、根本的に多重ループとなるこの問題を１重ループ前提のこれらの高階関数で書くのは多少骨が折れそうです。

なんか最近のtensorflowは動的グラフがどうのこうのとかいう噂を聞いたことがある気がしますが、追いきれていません。それに動的グラフの先駆けであるChainerのパフォーマンスを思い返すとあまり期待はできないかもしれません。

基本のアイデア

相互作用する粒子のペアの集合$A=\left\{(i, j)| i, j \in N, i \neq j\right\}$があったとき、$dx_{ij} = x_i - x_j$と書く。

$x_1, x_1, \cdots, x_1, x_2, x_2, \cdots, x_i, \cdots$
$x_2, x_3, \cdots, x_N, x_3, x_4, \cdots, x_j, \cdots$
上下の差を取ると、
$dx_{12}, dx_{13}, \cdots, dx_{1N}, dx_{23}, dx_{24}, \cdots, dx_{ij}, \cdots$
とnumpyでまとめて計算できそうな形で $dx_{ij}$が得られる。

あとはうまく$x_1, x_1, \cdots,$と$x_2, x_3, \cdots,$ の順になるように添字の順番を決めたリストを作っておくと、indexingの操作で必要な順に$x_i$を並べることができるだろう。

numpyのindexing

４つの粒子があり0, 1, 2, 3の順に四角形に並んでいるとします。相互作用の組は、(0, 1)、(1, 2)、(2, 3)、(3, 0)の辺と(1, 3)、(0, 2)の対角線の計６つです。

pythonにおいて、以下のようなリストを考えます。

i_idx = [0, 1, 2, 3, 1, 0]
j_idx = [1, 2, 3, 0, 3, 2]

そして、これのzipをとってみます。

print(list(zip(i_idx, j_idx)))
# [(0, 1), (1, 2), (2, 3), (3, 0), (1, 3), (0, 2)]

先ほどの相互作用の組がリストになりました。

続いて、４つの2次元座標を保持する4行３列のnumpy配列を用意します。

x = np.array([[0, 0], [0, 1], [1, 1], [1, 0]], dtype=float)
array([[0., 0.],
       [0., 1.],
       [1., 1.],
       [1., 0.]])

ここで、今回は以下のテクニックを使おうと思います。
numpyであれば、indexingを使って、次のように必要な成分をほしい順に並べられます。

x[i_idx, :]
array([[0., 0.],
       [0., 1.],
       [1., 1.],
       [1., 0.],
       [0., 1.],
       [0., 0.]])

このように2粒子のうちiに相当するものを、ループで出てくる順に並べることができました。同様にjに相当するものもx[j_idx, :]で並べられます。

そして、これらの粒子間の位置ベクトルは

dx = x[i_idx, :] - x[j_idx, :]
array([[ 0., -1.],
       [-1.,  0.],
       [ 0.,  1.],
       [ 1.,  0.],
       [-1.,  1.],
       [-1., -1.]])

と、とくにループ構文を使うことなく１行で書けました。これを使って、距離などもループを使わず書けます。

np.sqrt(np.sum(dx**2, axis=1))
array([1.        , 1.        , 1.        , 1.        , 1.41421356,       1.41421356])

またはnp.linalg.norm(dx, axis=1)でも同じ結果を得ます。

tensorflowには添字[]に整数listを直接叩き込むことができないのですが、sliceなど同様の操作ができる関数がありますので、この方向で実装ができます。

あとは、問題に応じてi_idxやj_idxを決めてやるだけです。

同様の発想で3体以上の相互作用も多重ループを顕に書かずに実装できるのではと思います。

Tensorflowの実装

ピタゴラスの三体問題とか、平面のバネ格子モデルとかで遊んだのですが、長くなったので気が向いたら別記事としてみようかと思います。

まとめ

以上、$\vec{F}$ の具体的な実装をtensorflowに一任することができました。まあ、例によってすごい重い（ピタゴラスの3体問題で半日とかかかる）のですが、sympyよりかは速いのではないかなと思います。

人によりますが、$\vec{F}$ のコーディングの時間とFortranなどの実行速度を鑑みると、10回とか繰り返すならFortranなどで従来通りのMDプログラムを書いた方がいいかなと。

補足

このネタで記事を書こうと思い立ったはじめのころ、座標更新演算子

e^{Tdt}: \vec{r} \leftarrow \vec{r} + \vec{v}dt\\
e^{Udt}: \vec{p} \leftarrow \vec{p} + \vec{F}dt

を

\theta \leftarrow \theta - \alpha \frac{\partial L}{\partial \theta}

というよくある機械学習の損失関数の最小化を使って、損失関数 $L$ をハミルトニアン $H$ 、学習率 $\alpha$ を時間刻み　$dt$ とすれば tf.train.GradientDescentOptimizer を使えるかなと思っていましたが、正準方程式では更新する変数と微分する変数が違うので、最適化アルゴリズムは使えないなという結論になりました。

補足２

この記事は一通り書いてから下書きで数ヶ月放置していたのですが、その間にtensorflow2が発表されました。これはtensorflow1.xのeagerモードがデフォルトになり、Sessionの概念がなくなるそうです。そうなるとこの記事の実装における議論は少々変えないといけないかもしれません。

---

1. 多くのハミルトニアンが２体間相互作用の和で書かれるのでとりあえず２体間相互作用を例に出しましたが、もちろん変角振動などの３体間以上の相互作用もあり、これらも同様に添字を抽出する操作が必要になります。 ↩