SVDで平面フィット by julia

当記事の目的

Juliaを使い始めたということで、個人的に実践的である例として3次元点群に対してSVD（特異値分解）による平面フィットをやってみたいと思います。

以下のことをjuliaではどう行うかという話になります。

• 単純なフォーマットのファイル読み込み
• 配列のスライスなどの簡単な操作
• ブロードキャスト
• SVD
• 3Dプロット

そして普段Python(Numpy)を使っていて、今回初めてjuliaを触った人間が新しいと思った点を重点的に説明します。

SVDで平面フィットが行える理論とPython, C++, Fortranでの実装は僕がQiitaで書いた記事、SVDで簡単平面フィッティングをご覧いただけたらと思います。

準備

• Julia 1.3.0

1.2では使えない関数があった気がする。

• 3D可視化用パッケージ

import Pkg
Pkg.add("Plots")
Pkg.add("PyPlot")

• 点群データ

三次元の点を上の記事のように作ってもいいのですが、ちょっとやってみたいこともあるので、実際の測定データを使ってみます。

「PCL IROS2011」あたりでググると
http://www.pointclouds.org/media/iros2011.html
というページにたどり着けるかと思いますが、その底あたりに「data」というリンクがあり、それは以下のURL：
http://www.pointclouds.org/assets/files/presentations/IROS2011-PCL-tutorial-data.zip
です。これを踏むとチュートリアル用に用意された3Dスキャナの詰め合わせが得られます。ところがこれはPCL（Point Cloud Library）のチュートリアルのため、PCL独自フォーマットのバイナリデータ（拡張子 pcd）です。
PCLはC++用ライブラリで他の言語には使いにくいし、そもそもC++でもPCLをリンクするとビルドが糞重いので、こんな簡単な例ではPCLはあまり使いたくないところ。ということで使いやすい形式、例えばxyz形式にします。
pcd形式を開くことのできる3D処理ソフトとして、CloudCompareがあります。これで例えばsharkというフォルダ内にあるファイルを開くと、以下の画像のような点群がみられるかと思います。

CloudCompareで点群を選択、XYZ形式で保存します。このファイルは以下のような内容で、sharkの例だと255000行程度あるかと思います。

-0.85433722 -0.56770289 1.46100008 254 254 254
-0.85505152 -0.57003433 1.46700013 254 254 254
-0.85574287 -0.57236570 1.47300005 254 254 254
-0.85293716 -0.57236570 1.47300005 254 254 254
-0.85417140 -0.57508576 1.48000002 254 254 254
-0.85135233 -0.57508576 1.48000002 254 254 254
-0.85433722 -0.56492001 1.46100008 254 254 254

一応、この数字の並びは以下のように座標と色情報を並べただけのフォーマットになります。

x座標 y座標 z座標 R G B

これを平面フィットの例題とします。

本編

ファイル読み込み

XYZ形式の点群はすべての行が同じ形式の単純なファイルのため、DelimitedFiles が使えます。

import DelimitedFiles
xyz_filename = "shark.xyz"
xyzdata = DelimitedFiles.readdlm(xyz_filename, ' ', Float64)
coord = xyzdata[:, 1:3]

3行目がファイル読み込み実行で、これで xyzdata の形状は (255000, 6) になります。これの後半の色情報はいらないので、 coord = xyzdata[:, 1:3] としてXYZ座標だけを取り出します。

あ、juliaのインデックスは1始まりです。Fortrannerとしてはとてもなじみ深い仕様です。

あと、これは点の数が多すぎるので、以下のように最初の10000点から1つ飛ばしに5000点だけ取ることにします。
ここでNumpyとは配列のスライスの仕方が異なります。Numpyではcoord[:10000:2, :] つまり array[start:stop:step]という表現になるのに対し、juliaではarray[start:step:last]というスライスになります。

coord = coord[:2:10000, :]

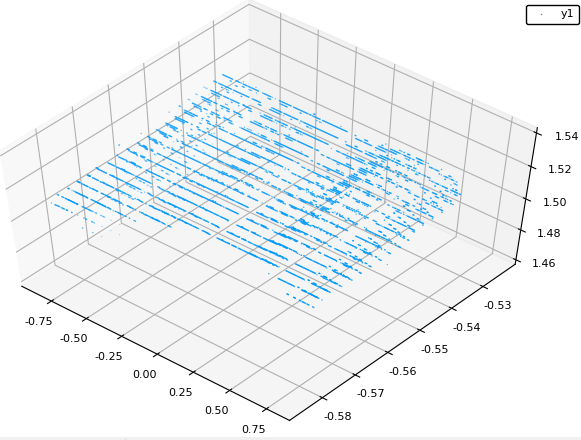
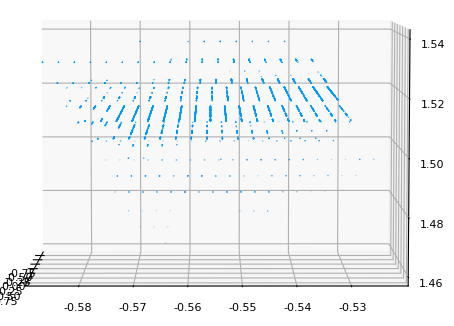
ちなみにこれで取り出された点群は以下のような見た目です。

たぶん壁の平面部分だけを取り出せています。

なんか構造が見えますが、これは前職での僕の経験が正しければ3次元再構築の時の特徴量の座標推定のとき、サブピクセル推定が甘いときに見えがちかなと。

SVDによる平面フィット

SVDで $ax + by + cz + d = 0$ の $a, b, c, d$ をどうやって求めるかを追っていきます。

重心を０に

全体の点群の重心を０にします。そのためには、coordの１次元目で平均をとり、すべての点からその座標を差っ引きます。

まず重心の座標の取得。Statistics を使います。

import Statistics
center = Statistics.mean(coord, dims=1)

続いて重心の座標を引きますが、coordが2次元の配列に対しcenterは1次元配列で、希望としてはcoordの１次元目を順番に回して、２次元目と center の差をとってほしいところです。これは Base にある broadcast を使います。

c0 = broadcast(-, coord, center)

c0 が重心を 0 になるように平行移動した座標です。

なお、numpyのように coord - center とすると、

ERROR: LoadError: DimensionMismatch("dimensions must match")

となってエラーで止まります。つまりブロードキャストは明示的にしないといけないようです。

SVD 実行

LinearAlgebra に普通に関数があります。

import LinearAlgebra
U, S, V = LinearAlgebra.svd(c0)

SVD自体はこれで完了です。ほしい平面のパラメータは V の最後のベクトルです。 Numpyだと V[-1, :] で取れますが、juliaでこうするとおかしなインデックスというエラーで止まります。では最後のインデックスをどう指定するかというと、juliaには end というキーワードがあります。

nv = V[end, :]

これで最後のインデックスを指定して値（ベクトル）を取り出すことができます。
なお、nv に平面の法線ベクトル、つまり $ax + by + cz + d = 0$ としたとき $\vec{n} = (a, b, c)$ が入っています。

残るパラメータは dです。原点を通る平面の法線ベクトルが $\vec{n}$ のとき、この平面とある点 $\vec{r}$ との距離は $\vec{r}\cdot\vec{n}$ になります。ということで d は各点ごとに平面との距離を計算し、それを平均すれば求められますが、行列演算を用いれば1行で済みます。
Juliaでは行列とベクトルの * 演算で行列の各行とベクトルとのドット積を計算でき、それを配列として得ることができます。つまり * は普通の行列積です。それをそのまま Statistics の平均をとる関数 mean に渡します。

d = - Statistics.mean(coord*nv)

平面のフィッティングは以上で終わりです。後は可視化するという蛇足です。

可視化

平面の四隅

まず、サンプル点群においてx, y, z座標の最大値、最小値を求めます。

minxyz = minimum(coord, dims=1)
maxxyz = maximum(coord, dims=1)
x0 = minxyz[1]
x1 = maxxyz[1]
y0 = minxyz[2]
y1 = maxxyz[2]

おそらく平面の四隅になるであろう4点は x, y座標の最小値、最大値をそれぞれ選択した4通り。これらをまとめた2次元配列を作ってしまいます。これで行列演算で4点をまとめて処理できます。

corner_xy = [x0 y0; x1 y0; x0 y1; x1 y1]

要素のセパレータがコンマ,ではなくてスペース だけだった。

これらに対応するz座標を計算します。平面の法線のxy座標だけを取り出した2次元ベクトルをnvxyとします。

corner_z = - broadcast(+, corner_xy*nvxy, d)/nv[3]

corner_xyが 4x2の配列なのに対し、corner_z は長さ4の一次元配列です。

プロット

Juliaの Plots はバックエンド（レンダリングエンジンみたいなもの）が GL、Plotly、PyPlotなどから選べるのですが、今回はPyPlotを用いることにします。

• スクリプトファイルから画像生成ではなくマウス操作できるGUIを表示したい
• 点群と平面を重ねて表示したい
• 点の数がとても多くなりそう

という状況で、 Plotlyはパフォーマンスとしては良さそうだったのですが、平面の表示に難があったので見送り、とりあえずそこそこのパフォーマンスでうまくいったPyPlotを使うことにしました。

まず Plotsをインポートして、そのバックエンドをPyPlotにします。

import Plots
Plots.pyplot()

簡単にプロットします。ここで点群はさらに奇数番目の点だけ2500点をプロットすることにします。どうやって奇数番目だけの点を取り出すかですが、例えばx座標が欲しい場合、Numpyでは coord[::2, 0]として得ます。つまりはじめと終わりを省略すると最初から最後までを見てくれます。
一方Juliaでは前述のとおりendキーワードを使うことで、coord[:2:end, 1] として奇数番目だけを取り出した配列を得ます。そしてそのままそれを点をプロットする scatter に渡します。

Plots.scatter(coord[:2:end, 1], coord[:2:end, 2], coord[:2:end, 3], markersize=1, markerstrokewidth=0)

marker云々のオプションは点の大きさをできるだけ小さくするためです。

最後に平面の表示。

Plots.plot!(corner_xy[:, 1], corner_xy[:, 2], corner_z, st=:surface, show=true)

これは関数面 st=:surface として表示します。 また、この描写をしてから画面表示をしてほしいので show=true とします。 ここで plotでなくplot!としていますが、なぜかそうしないとscatterで描写した分が消えました。

この２つを続けて呼び出すことで、下図のように点群と平面を重ねて表示できます。

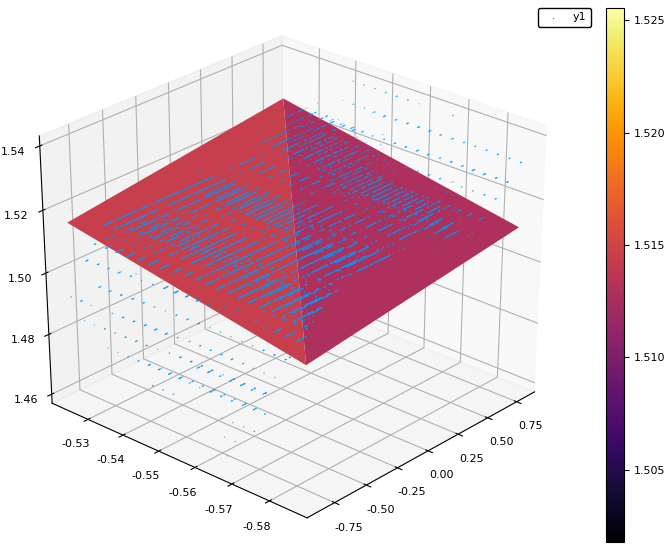
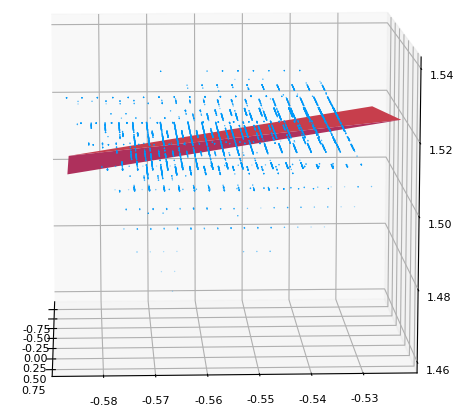
SVDによる平面フィットもまあまあうまくいっているように見えます。

グラフが見えない場合

なお、スクリプトファイルを実行する (julia hoge.jlみたいに実行する)場合、なぜかGUI表示してもそのまま処理が進み、スクリプトが終了してしまいグラフが見えません。それに備え、 plot!の後に処理を一時停止させる行を追加するとグラフが見えます。

x = readline()

これは単純に標準入力待ち状態にしているだけです。

終わりに

こんな感じでjuliaも線形代数的な処理は、Numpyほどでないにしてもかなり簡単に書けるようです。噂によると速度も出るらしいので、これは結構有用かなと。

ちなみにPCLはいま開発どうなってるんだろう。公式Webページの最新情報が2014年で止まっているのが気になる。

おまけ

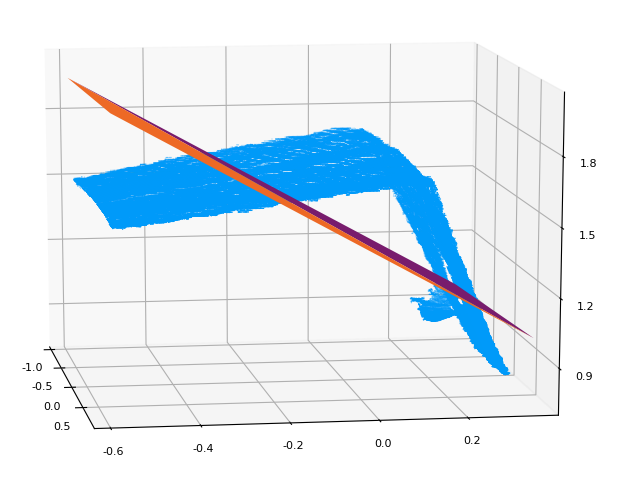
サンプルの全部分を使った場合。

描写めっちゃ重い。ちなみにPyPlotなので、点と平面の重ね順がおかしいです。