SVD(特異値分解、singular value decomposition)というものがあります。
これは誤解を恐れずに言えば、最小二乗法の1つの表現となっています。
個人的な話になるのですが、3次元上の点群に対して平面をフィットしたいことがまれに良くあります(普段は用が無いのですが、ひとたび用事ができるとすごい使う)。
それまでは必要なたびにググッていたのですが、正直手間ですし、先日はとうとう見つからなくなったので、
いっそ自分のメモも兼ねて書いてしまおうと思います。
ちなみに、平面以外にも一部の曲面へのフィットにも応用できるようです。
数学
平面は次の式を考えます。
ax + by + cz + d = 0
幾何学的な意味としては、$\vec{n}=(a, b, c)$は平面の法線ベクトル、$d$は原点と平面の距離に相当します。
さて、ここに3次元空間中に$N$個の点があるとします。
r = \left(\begin{matrix}
x_1 & y_1 & z_1 \\
x_2 & y_2 & z_2 \\
&\vdots& \\
x_N & y_N & z_N
\end{matrix}\right)
もしこれらが先ほどの平面上にあるなら、
\left(\begin{matrix}
x_1 & y_1 & z_1 \\
x_2 & y_2 & z_2 \\
&\vdots& \\
x_N & y_N & z_N
\end{matrix}\right)
\left(\begin{matrix}
a \\ b\\ c
\end{matrix}\right)
+ d = \left(\begin{matrix}
0 \\ 0\\ \vdots \\ 0
\end{matrix}\right)
となります。点群の重心を原点に持ってきて、$d=0$とすると
c = \frac{1}{N}\sum_{i=1}^N\left(x_i, y_i, z_i \right)\\
r_0 = r - (cを縦にN個並べた行列)
\\
r_0\left(\begin{matrix}
a \\ b\\ c
\end{matrix}\right) = \left(\begin{matrix}
0 \\ 0\\ \vdots \\ 0
\end{matrix}\right)
となります。
ここで、各点の座標$r$が既知で平面のパラメータ$a, b, c, d$が未知だった場合について考えます。普通はこのような状況でしょう。
もし点の数 = 空間の次元数であれば行列$r$は正方行列になります。すると固有値、固有ベクトルを考えることができて、
r_0\vec{v} = \lambda\vec{v}
から、$\lambda = 0$ の場合を考えれば $\vec{v} = (a, b, c)$となります。
ですが、$r$は正方行列ではありません。点の数が非常に多く、縦長の行列であることが普通だと思います。そこで表題のSVDを使います。
SVDでは固有値ではなく、特異値$\Sigma$として得られます。
ノイズが含まれている時や同一平面にないサンプルが含まれているときなど、$\Sigma_i = 0$ のものがない場合もあります。そのときは一番0に近いもので妥協します。この場合$\Sigma_i$ は回帰の誤差に相当します。
これで分かるのは$(a, b, c)$だけですが、これらががわかれば、サンプルから適当な1点 $\vec{r_i}$ を取ってきて
(a, b, c) \cdot \vec{r_i} + d_i = 0\\
d_i = - (a, b, c) \cdot \vec{r_i}
として$i$番目のサンプルにおけるパラメータ$d$の回帰値$d_i$がわかりますので、
$d = \frac{1}{N}\sum^N_{i=1}d_i$と平均をとってやれば、無事平面のパラメータが得られます。
python
下ごしらえ
まず、元になる平面のパラメータをランダムに設定します。
phi0 = random.random()*np.pi
theta0 = random.random()*np.pi
v0 = np.array([math.sin(phi0)*math.cos(theta0), math.sin(phi0)*math.sin(theta0), math.cos(phi0)])
d0 = random.random()*10.0
v0が正解の平面パラメータ$a$、$b$、$c$で、d0が$d$の値になっています。三角関数を適宜使ってやることで$\sqrt{a^2 + b^2 + c^2} = 1$となるようにしています。
サンプルの3次元点群を作る関数と、確認用出力のための関数を用意します。
def create_sample(nv, d, N):
""" nv: np.array of (a, b, c), |nv| = 1 """
""" nv*r + d = 0 """
# dxyzはノイズ
dxyz = np.random.random(3*N).reshape(3, N)*0.005
x = np.random.random(N)*2 - 1.0 + dxyz[0, :]
y = np.random.random(N)*2 - 1.0 + dxyz[1, :]
z = - (x*nv[0] + y*nv[1] + d)/nv[2] + dxyz[2, :]
return (x, y, z)
def print_xyz_meshlab(xs, ys, zs):
for v in zip(xs, ys, zs):
print("{} {} {}".format(*v))
print_xyz_meshlabはそのままMeshlabというソフトで読み込めるxyzファイル形式を出力する関数です。こうやって定義された関数で
xs, ys, zs = create_sample(v0, d0, 2000)
print_xyz_meshlab(xs, ys, zs)
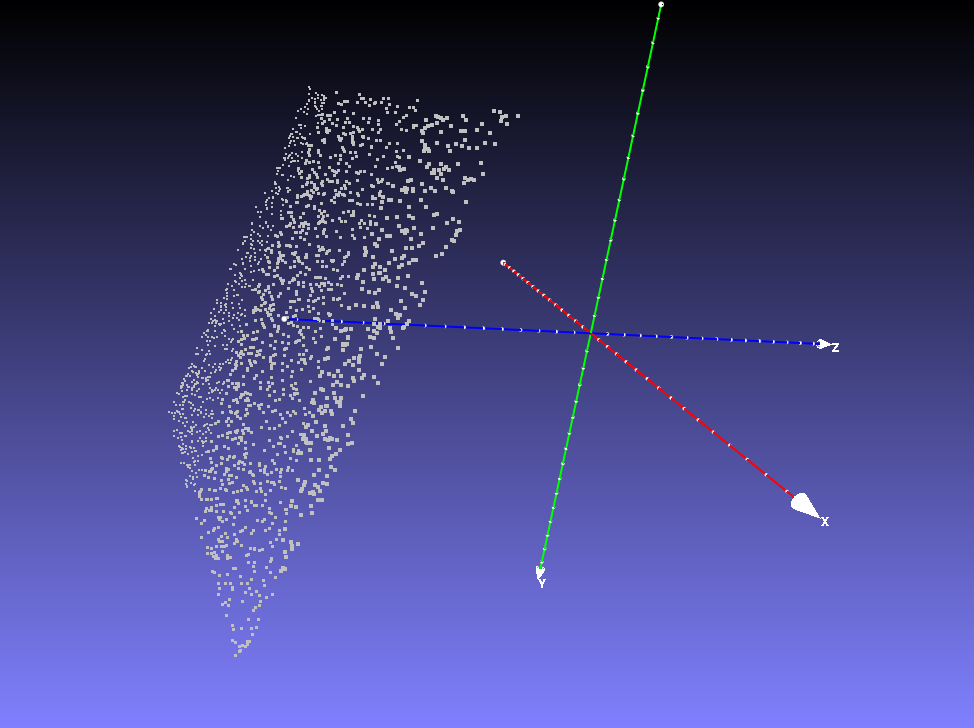
としてやり、出力を適当なxyzファイルに保存してMeshlabでみてやると、
こんな感じの点群ができています。これに平面をフィットします。
平面フィット
先の数学の話をそのままnumpyで表現しますと、
def find_plane(xs, ys, zs):
r = np.c_[xs, ys, zs]
# サンプル点群の重心、x, y, zの3つの成分
c = np.mean(r, axis=0)
# サンプル点群の重心を原点に移動
r0 = r - c
# SVD分解
u, s, v = np.linalg.svd(r0)
# sの最小値に対応するベクトルを取り出す
nv = v[-1, :]
# サンプル点群の平面と原点との距離
ds = np.dot(r, nv)
param = np.r_[nv, -np.mean(ds)]
print(param)
となります。paramには回帰で得られた$a, b, c, d$が入っている配列で、今回はそのまま出力して終わります。
SVDでは行列$A$を$A=U\Sigma V^T$と分解します。u, s, vにそれぞれ$U$、$\Sigma$の対角成分、$V^T$が入ります。$V^T$の各列に$s$の値に対応する固有ベクトルのようなものが入っています。
今回用があるのは最小の$\Sigma$に対するベクトルだけで、numpyなどの大体の数値計算ライブラリでは$\Sigma$を降順で出力しますので、$v$の最終列のみをv[-1, :]という形で取り出しています。
結果
def main():
phi0 = random.random()*np.pi
theta0 = random.random()*np.pi
v0 = np.array([math.sin(phi0)*math.cos(theta0), math.sin(phi0)*math.sin(theta0), math.cos(phi0)])
d0 = random.random()*10.0
xs, ys, zs = create_sample(v0, d0, 2000)
print("{} x + {} y + {} z + {} = 0".format(*v0, d0))
print("----")
find_plane(xs, ys, zs)
if __name__ == '__main__':
main()
これを実行しますと
-0.9843900597418571 x + 0.07652887761887706 y + -0.15849145457032648 z + 6.44296543038493 = 0
----
[ 0.98439044 -0.07652614 0.15849038 -6.44332474]
となり、平面をうまくフィット出来たことがわかります。正負が逆ですが、$ax + by + cz + d = 0$という式から分かるように、$a, b, c, d$の符号がすべて同じか、すべてひっくり返っていれば大丈夫です。
なお、見つけたパラメータについて、find_plane関数内にて
delta = np.dot(r, nv)
print("minimam sigular val", s[-1])
print("RMSD", np.sqrt(np.sum(delta**2)))
と追加してやると
minimam sigular val 0.010384392771151689
RMSD 0.010384392771151694
という出力が得られます。これから、特異値はフィット時の平均二乗偏差であることが確認できます。
他の言語
PythonではNumpyの力で
- 行列におけるReduction関数の次元限定
c = np.mean(r, axis=0)
- ベクトル→行列のブロードキャスト
r0 = r - c
- SVD
を当たり前に行っていますが、他の言語ではどうなるかやってみます。
あと、変数名がpythonのものと違っていたりしていますが、ご容赦ください。
C++
以下のヘッダをインクルードします。
# include <iostream>
# include <random>
# include <vector>
# include <math.h>
# include <Eigen/Core>
# include <Eigen/SVD>
Eigen/SVDを追加したら、コンパイルの時間がなんかすごい伸びました。
点群生成
Eigen::MatrixX3d make_sample(const std::vector<double> params, const int N){
double a = params[0];
double b = params[1];
double c = params[2];
double d = params[3];
Eigen::Matrix<double, Eigen::Dynamic, 3> r(N, 3), dr(N, 3);
r.setRandom();
dr.setRandom(); // ノイズ
dr *= 0.01;
r.col(2) = - (r.col(0) * a + r.col(1) * b + d * Eigen::MatrixXd::Ones(N, 1))/c;
r += dr;
return r;
}
Meshlab用の出力は次のようになります。
void print_xyz_meshlab(Eigen::MatrixX3d r){
Eigen::IOFormat meshlab_xyz(Eigen::StreamPrecision, Eigen::DontAlignCols);
std::cout << r.format(meshlab_xyz) << std::endl;
}
Meshlabではxyz形式のカラム分割用スペースが連続してはいけない(半角スペース1字のみ)とする必要がありますので、std::coutにEigen::Matrixを流し込んだ時に列揃え用のスペースを増やさないように設定を変えてやります。
平面フィット
std::vector<double> find_plane(Eigen::MatrixX3d r){
auto centroid = r.colwise().mean();
Eigen::MatrixX3d r0 = r.rowwise() - centroid;
Eigen::JacobiSVD<Eigen::MatrixX3d> svd(r0, Eigen::ComputeFullV);
Eigen::Vector3d nv = svd.matrixV().col(2);
double d = - (r*nv).mean();
std::vector<double> ret(nv.data(), nv.data() + 3);
ret.push_back(d);
return ret;
}
ブロードキャストとか一部次元のReduction関数については、基本的にrowwise、colwiseを使うという感じですね。
x, y, zの各次元の平均はcolwise。これは次元ごと、つまり列ごとに平均とるということでわかりやすいです。
ベクトル→行列へのブロードキャストは、行列から見ると行ごとにベクトルの引き算を行っているので、行列の方からrowwiseを呼び出してベクトルに歩み寄っています。
$V^T$の最終列を取り出すには、$V$は3行3列の行列なので、明示的にインデックス2を指定してsvd.matrixV().col(2)とします。
メイン関数
int main(void){
int N = 1000;
std::vector<double> params(4);
double phi, theta;
std::random_device rd;
std::mt19937_64 mt(rd());
phi = ((double) mt())/mt.max()*M_PI;
theta = ((double) mt())/mt.max()*M_PI;
params[0] = sin(theta)*cos(phi);
params[1] = sin(theta)*sin(phi);
params[2] = cos(theta);
params[3] = (((double) mt())/mt.max() - 0.5)*5.0;
auto r = make_sample(params, N);
auto p = find_plane(r);
std::cout << "Original parameters:" << std::endl;
std::cout << params[0] << " " << params[1] << " " << params[2] << " " << params[3] << " " << std::endl;
std::cout << "Fitted parameters:" << std::endl;
std::cout << p[0] << " " << p[1] << " " << p[2] << " " << p[3] << " " << std::endl;
return 0;
}
与えられた点群の座標がrでN行3列の行列、pがフィットして得られた平面パラメータです。paramが正解の平面パラメータとなります。
これをコンパイルして実行します。
$ g++ -o svd_cpp -I/usr/include/eigen3 -std=c++11 svd.cpp
$ ./svd_cpp
Original parameters:
-0.748355 0.61532 0.247683 -0.586658
Fitted parameters:
0.74869 -0.614927 -0.247645 0.586486
Fortran
点群生成
function make_samples(a, b, c, d, N) result(r)
double precision, intent(in) :: a, b, c, d
integer, intent(in) :: N
double precision :: r(N, 3)
double precision :: x(N), y(N), dr(N, 3)
call random_number(x)
call random_number(y)
call random_number(dr) ! ノイズ
dr = dr*0.02 - 0.01 ! ノイズを -0.01〜0.01の値に
x = x*2.0 - 1.0
y = y*2.0 - 1.0
r(:, 1) = x
r(:, 2) = y
r(:, 3) = - (a * x + b * y + d)/c
r = r + dr
end function make_samples
Meshlab用の出力
subroutine print_xyz_meshlab(r, N)
integer, intent(in) :: N
double precision, intent(in) :: r(N, 3)
integer :: i
do i = 1,N
write(*, '(*(f0.6,:," "))') r(i, :)
enddo
end subroutine print_xyz_meshlab
小数点以下を6桁まで、区切り文字はスペース1つ、データがなくなったら改行という指定をします。
平面フィット
SVD計算にはLAPACKを使います。dgesvdを2回読んでいますが、1回めはworkの適切な長さ取得用、2回目がSVD実行用です。このあとrはインプレースで書き換えられています。
Fortranは基本参照渡しのため、svd_get_minVを呼んだあとはこれに渡したr0は使い物にならなくなります。
function svd_get_minV(r, N) result(v)
integer, intent(in) :: N
double precision, intent(in) :: r(N, 3)
double precision :: v(3)
double precision :: U(N, N), s(3), dummy(1, 1), Vt(3, 3)
double precision, allocatable :: work(:)
integer :: lwork, info
lwork = -1
call dgesvd('N', 'A', N, 3, r, N, s, U, N, Vt, 3, dummy, lwork, info)
lwork = max(N + 12 + 64*(N + 3), nint(dummy(1, 1)))
allocate(work(lwork))
call dgesvd('N', 'A', N, 3, r, N, s, U, N, Vt, 3, work, lwork, info)
v = Vt(3, :)
end function svd_get_minV
function find_plane(r, N) result(p)
integer, intent(in) :: N
double precision, intent(in) :: r(N, 3)
double precision :: p(4)
double precision :: centroid(3), r0(N, 3), nv(3), d, Vt(3, 3)
centroid = sum(r, 1)/N
r0 = r - spread(centroid, 1, N)
nv = svd_get_minV(r0, N)
d = - sum(matmul(r, reshape(nv, (/3, 1/))))/N
p(1:3) = nv
p(4) = d
end function find_plane
Reduction関数の次元限定(sumの二番目の引数の1)はできますが、ベクトル→行列のブロードキャストはできなかったので、spread関数を使って自力でブロードキャストします。
あと、matmulというのは行列同士の積ですので、行列とベクトルの積というのはベクトルをN行1列の行列としてmatmulに渡す必要があります。ということで点群の座標rと平面の法線ベクトルnvの積は
matmul(r, reshape(nv, (/3, 1/)))としてnvを行列にreshapeしてやります。
ちょっとハマった点。
- Fortranでは長さNの配列にそれより長い配列を = で代入してもトリミングして代入してしまいます(というかただのバッファオーバーフローかも)。そのため
sumの2番めの引数を間違えても要素数が違うエラーが出ません。 -
dgesvdに2次元配列を渡していますが、LAPACK内部には先頭アドレスを渡しているのと変わりありません。そのためrの転置行列を渡したとしても内部的には問題がなく、間違った値が得られるのみで気づきにくいです。
結果
上で定義しましたmake_samples、find_plane、svd_get_minVを適当なモジュール、ここではfunctionsで定義しておきます。
module functions
implicit none
contains
(中略、make_samplesやfind_plane、svd_get_minVを定義)
end module functions
program find_plane_svd
use functions
implicit none
double precision :: a, b, c, d
double precision :: theta(3)
double precision, parameter :: pi = acos(-1.d0)
double precision, allocatable :: r(:, :)
double precision :: param(4)
integer :: N
call random_seed_clock()
call random_number(theta)
theta = theta*pi
a = sin(theta(1)) * cos(theta(2))
b = sin(theta(1)) * sin(theta(2))
c = cos(theta(1))
d = theta(3) - pi*0.5
N = 1000
write(*, *) "Original parameters"
write(*, *) a, b, c, d
r = make_samples(a, b, c, d, N)
! call print_xyz_meshlab(r, N)
param = find_plane(r, N)
write(*, *) "Fitted parameters"
write(*, *) param
end program find_plane_svd
コンパイルと実行。
$ gfortran -o svd_fortran svd.f90 -L/usr/lib -llapack
$ ./svd_fortran
Original parameters
-0.37288036639007788 0.20059034266939257 -0.90593804798594091 0.70742336734838362
Fitted parameters
-0.37301925499840788 0.20023534536112303 -0.90595940409520836 0.70720777531295187
その他
所詮は最小二乗法、ノイズというか外れ値には弱いです。
- Outlierが無いと断言できない
- 室内を全体的に3Dスキャンして床とか壁の平面の式を回帰したい
などといったように、最小二乗法では余計なものに答えが引っ張られそうな状況では、RANSACなどの他のアルゴリズムを使う方がいいかなと思います。
追記
最初に平面を平行移動しましたが、そうではなくベクトルの次元を $d$ 用に1つ追加してみたケース、また最小二乗法ではなく絶対値誤差の最小化でやってみた場合の記事を書きました。
追記2
Juliaでやった場合も書きました。
この記事の目的はどちらかというとjuliaの導入です。