解いた式
ラグランジアン
$$
L = K - U
$$
を時間積分した
$$
S = \int L \mathrm{d}t
$$
を馬鹿正直に数値的に最小化したら、それっぽい軌跡が得られました。
2次元平面での重力ポテンシャルの公転運動です。
お断り
今回も機械学習の話ではありません。
もうちょいくやしく
数値的に解くので、位置 $\vec{r}(t)$ は時間について離散的な関数となります。$N$ ステップの軌跡だと思うと、軌跡はベクトルみたいに書けます。
$$
x = \Bigl(\vec{r}(0), \vec{r}(\Delta t), \cdots, \vec{r}(N\Delta t) \Bigr)^\mathrm{T}
$$
速度は単純な差分で書けます。
ある時間ステップ $i$ では、その前後の成分の差分で速度が計算できます。テイラー展開の1次までとる発想です。
\vec{p}(i\Delta t) = \frac{1}{2\Delta t}\Bigl(\vec{r}\left((i + 1)\Delta t\right) - \vec{r}\left((i - 1)\Delta t\right)\Bigr)
$p$は普通は運動量に使う記号ですが、速度に使っています。これを行列表記にしますと
v = \frac{1}{2\Delta t}\left(
\begin{matrix}
-2 & 2 & 0 & 0 & \cdots \\
-1 & 0 & 1 & 0 & \cdots \\
0 & -1 & 0 & 1 & \cdots \\
& & \vdots & & \\
0 & \cdots & -1 & 0 & 1 \\
0 & \cdots & 0 & -2 & 2 \\
\end{matrix}
\right)
\left(
\begin{matrix}
\vec{r}(0) \\
\vec{r}(\Delta t) \\
\vec{r}(2\Delta t) \\
\vdots \\
\vec{r}((N-1)\Delta t) \\
\vec{r}(N\Delta t) \\
\end{matrix}
\right)
1番目と$N$ 番目の成分(つまり端、最初と最後)はとなりの成分との差とします。
差分を取る行列を $D = \frac{1}{2\Delta t}(\cdots) $としますと、
v = Dx
になります。
以降、$x$, $v$の$i$ステップ目の成分は添え字で表記することにします。
x_i = \vec{r}(i\Delta t)\\
v_i = \vec{p}(i\Delta t)
また運動の途中で質量 $m$ は一定だとします。
位置と速度が定義されたので、各時間ステップでの運動エネルギー
K_i = \frac{1}{2}mv_i^2
とポテンシャル
U_i = G\frac{mM}{\left(x_i - \vec{R}\right)^2}
が書けます。
ここで$G$は重力定数、$M$は公転中心の質量、$\vec{R}$は公転中心の座標とします。今回は$G=1$、$M=1$、$\vec{R}=0$としてしまいます。
最後に、各時間ステップごとのラグランジアン
L_i = K_i - U_i
を求めた後、それを全ステップにわたって合計した作用
S = \sum_i \Delta t L_i
が計算できます。
さて、最初の位置 $x_1$ と最後の位置 $x_N$ を固定し、その間の $x_i$ をいろいろ動かして、$S$を最小化させてみることを考えます。
最小作用の原理
変分的に書くと、
\delta S = 0
となり、自然界はこれを満たすような位相空間中の軌跡を取るというのが、解析力学の教えるところです。
ここから運動方程式などのハミルトン力学が派生していきます。つまりこの原理は普通は理論の礎になるもので、そのまま解く対象にはならないなという印象です。
$S$ は普通は位置と共役運動量 $r$, $p$の関数なのでこのように変分的に書きますが、
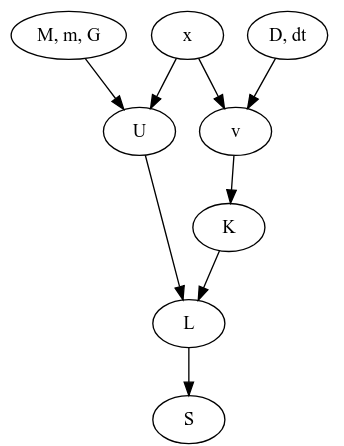
今回の話の依存関係を追ってみますと、
というグラフになっています。ここで$M, m, G, D$は系が決まれば定数となるものです。となれば独立に変更できそうなのは$x$だけですね。そして$x$は2次元中の$N$個の点列だと思うと、$2(N-2)$ 個のパラメータがあるように見えます。すると、
x(軌跡) = \mathop{\rm arg~min}\limits_x \left[S\right]
として、なんかオプティマイザがつかえそうですね。
Tensorflowのtrainerの出番です。
実装開始
ライブラリ
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
注意
ここでのtensorflowのバージョンは1.xです。Eagerモードがデフォルトになる2.xでは実装を変えなければなりません。
定数
G = 1.0
m = 1.0
Mc = 1.0
Mm = Mc*m
fp = tf.float64
Nstep = 500
Ndim = 2
Time_all = 6.4
dt = Time_all/Nstep
Time_allは軌跡の始点と終点の間にかかった時間で、dtはそれを総ステップ数Nstepで割ったものになります。
位置
r_init = tf.get_variable("position_init", shape=[1, Ndim], dtype=fp, trainable=False)
r_fin = tf.get_variable("position_final", shape=[1, Ndim], dtype=fp, trainable=False)
r_path = tf.get_variable("position_path", shape=[Nstep - 2, Ndim], dtype=fp)
r = tf.concat([r_init, r_path, r_fin], 0)
微分用行列
d_mat = np.eye(Nstep, k=1)
d_mat = d_mat - d_mat.T
d_mat[0, 0] = -1
d_mat[-1, -1] = 1
d_mat = tf.constant(d_mat/2)/dt
上で出てきた式を頑張ってnumpy行列にし、最後にtf.constantに渡しています。
速度
dr = tf.matmul(d_mat, r)
ここで、rの形状は(N, 2)で、d_matは(N, N)なので、drは(N, 2)の形状のtf.Tensorです。
運動エネルギー
vr_i = tf.reduce_sum(dr**2, axis=1)
K_i = 0.5*vr_i*m
各成分を2乗して足したらベクトルの長さの2乗ですね。
reduce_sumにaxisを渡しているので、dr**2の形状(N, 2)のうちの2のほうが総和の対象となります。そのためvr_iの形状は(N, )です。
位置エネルギー
rr_i = tf.rsqrt(tf.reduce_sum(r**2, axis=1))
U_i = - G*Mm*rr_i
ラグランジアン
L_i = K_i - U_i
作用
S = tf.reduce_sum(L_i)*dt
dtはなくてもいいんじゃないかな。
最小化
optimizer = tf.train.AdamOptimizer(0.05)
minimize = optimizer.minimize(S)
困った時のAdam。結果のところにありますが、一応GradientDescentも試しています。
初期座標
代入演算
r_path_0 = tf.placeholder(fp, shape=[Nstep - 2, Ndim])
r_init_0 = tf.placeholder(fp, shape=[1, Ndim])
r_fin_0 = tf.placeholder(fp, shape=[1, Ndim])
init_assign = [tf.assign(r_path, r_path_0), tf.assign(r_init, r_init_0), tf.assign(r_fin, r_fin_0)]
initializer = tf.global_variables_initializer()
rは最小化の対象化でtf.Variableです。これに所定の初期値を与える方法として、
-
tf.get_variablesのinitializerオプションにて、tf.constant(value=hogehoge)とする。 - 受け皿の
tf.placeholderを用意し、tf.assignで上書き
が考えられます。今回はr_pathの定義が初期値を決める処理より先に来てしまったので前者が使いにくく、後者としました。
実際の値
r1 = np.array([1.0, 0.0])
r2 = np.array([0.0, 1.0])
r3 = np.array([-1.0, 0.0])
r4 = np.array([0.0, -1.0])
r5 = np.array([1.0, 0.0])
rs = np.c_[r1, r2, r3, r4, r5].T
ts = np.arange(5)/4
ts_interp = np.arange(Nstep)/(Nstep - 1)
x_interp = np.interp(ts_interp, ts, rs[:, 0])
y_interp = np.interp(ts_interp, ts, rs[:, 1])
r0_np = np.c_[x_interp, y_interp].reshape(Nstep, Ndim)
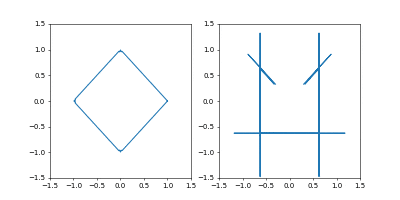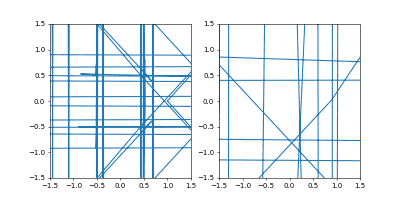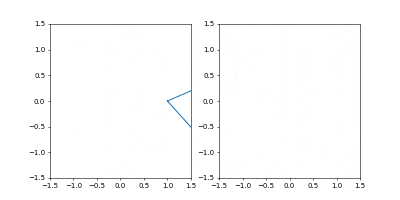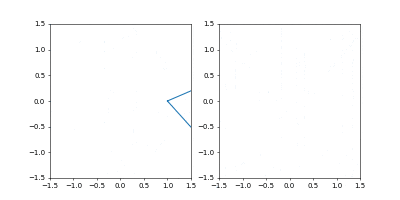
$(1,0), (0, 1), (-1, 0), (0, -1), (1, 0)$ の順に原点周りを1周し、その間を適当に補間した感じです。つまり原点周りに菱型に回る軌跡を初期状態としました。
rsがその通って欲しいチェックポイント5点を並べたもので、tsがその時刻です。ここでは開始を$t=0$, 終点を$t=1$にしました。注意:ここでの$t$はMD中での$t$とは異なり、ただのnp.interp用の横軸です。
実行
可視化のmatplotlibとその初期化
fig = plt.figure()
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
lines1, = ax1.plot(x_interp, y_interp)
lines2, = ax2.plot(x_interp, y_interp)
ax2.set_xlim((-1.5, 1.5))
ax2.set_ylim((-1.5, 1.5))
ax1.set_xlim((-1.5, 1.5))
ax1.set_ylim((-1.5, 1.5))
ax1は左半分で座標を、ax2は右半分で速度をプロットします。
が、ここでは速度の計算がまだなされていないので、座標をプロットしてお茶を濁します。
セッション
with tf.Session() as sess:
sess.run(initializer)
初期値代入
sess.run(init_assign, feed_dict={r_path_0: r0_np[1:-1, :], r_init_0: r0_np[0:1, :], r_fin_0: r0_np[-1:, :]})
最小化実行
step = 0
while True:
sess.run(minimize)
step += 1
可視化
if step%2 == 0:
r_t = sess.run(r)
lines1.set_data(r_t[:, 0], r_t[:, 1])
v_t = sess.run(dr)
lines2.set_data(v_t[:, 0], v_t[:, 1])
plt.pause(0.001)
2イテレーションごとに、matplotlibのax2にセットされた値をset_dataで更新していきます。
たまに初期ウィンドウから大きく外れるので、set_xlim set_ylimで適宜調整します。
終わるときは、端末をアクティブにしてCtrl+Cです。
結果
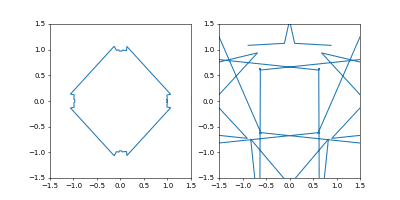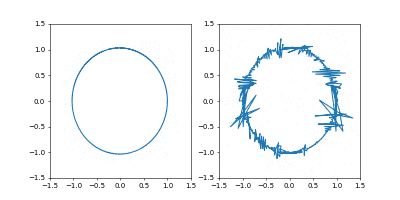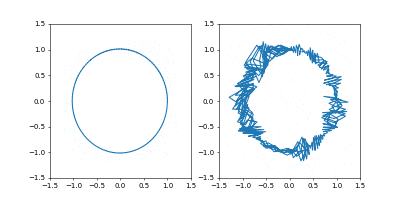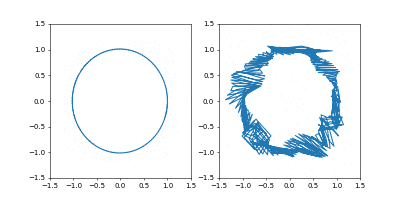
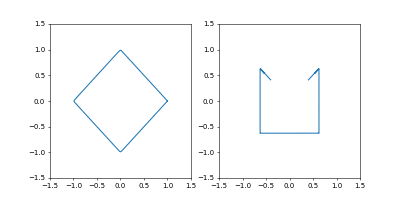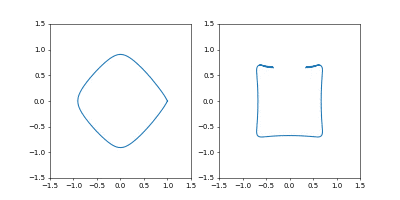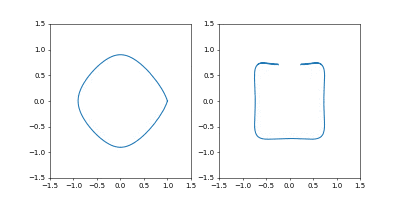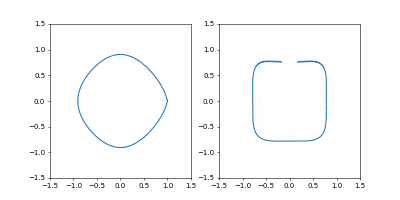
左が位置、右が速度の図です。
- Adam
学習率は $0.05$ です。
GIF動画1周が1000イテレーションです。
収束が近づいた時に暴れるのが難点ですね。真剣にやるなら、収束が進んだ段階で学習率を変えたり、オプティマイザを変えるなどの工夫がいることでしょう。
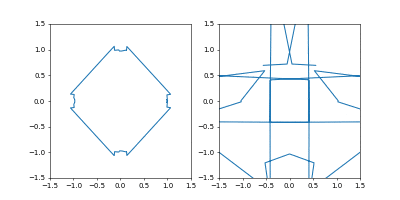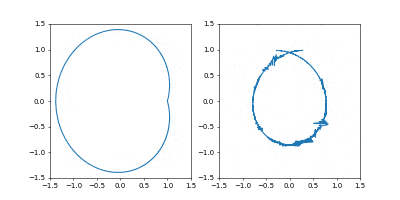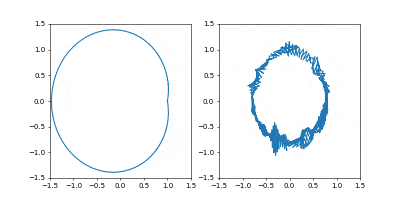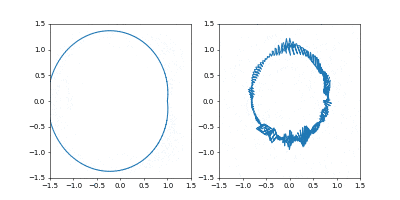
- GradientDecent
まず、Adamの時と同じ学習率 $0.05$ にすると発散しました。
動画1周が250イテレーションくらい。
学習率を $0.01$にすると発散はしませんでしたが、非常に収束が遅くなりました。
動画一周で1000イテレーション。フレームレートはAdamのものと同じです。
- おまけ
AdamでTime_all = 10.0としてみました。
1000イテレーションでは若干収束には届きませんでしたが、1周にかかる時間を増やしたのに合わせて先ほどの軌跡よりも原点から遠くに行って、速度も小さくなっているのがわかると思います。
余談
今回は経路の最初と最後を固定しました。
もしここも動くようにすると、運動エネルギーを小さく、位置エネルギーを大きくすれば作用も小さくなりますが、これは今回の系では無限遠で静止というのになってしまいそうですね。
まあ動かないまでもある程度の束縛(一周する=最初と最後の位置が一緒である)とかを課したもとでの最小化とかも考えられますが、今回はこの辺にしておきます。
野望
経路積分