【第一弾】小売売上予測でProphet vs LightGBMを戦わせてみた話

はじめに

本記事は Neural Group Advent Calendar 2025 10 日目の記事です。

普段は業務でデータ分析をしていますが、今回は「需要予測モデル」にフォーカスして、小売売上の予測に挑戦してみます。

小売の現場では、「来月の売上ってどれくらい？」という相談を受けることが多いです。しかし、売上には季節性・キャンペーン・曜日など多くの要因が絡むため、簡単に答えることはできません。

そこで本記事では、代表的な時系列予測手法 Prophet と LightGBM を使い、以下の流れで予測を行います。

1. 小売特有のクセを含んだダミーデータの生成
2. 前処理とEDAでデータの特徴を把握
3. Prophetによるベースライン予測
4. LightGBM＋ラグ特徴量によるモデル構築
5. 精度評価とモデル比較

それでは、順番に見ていきましょう。

コード

本記事のサンプルコードは GitHub リポジトリ にて公開しています。
動かす場合の環境構築手順も README に記載していますので、そちらを参照してください。

1. 小売特有のクセを含んだダミーデータの生成

まず、リアルなダミーデータを作ります。今回は アパレル店舗 の日次売上を想定して生成します。
※以下はあくまでサンプルです。実際の売上とは異なりますが、アパレル業界でよく見られる季節性やイベントの動きを示す例としてご覧ください。

• 初売り（1月）：福袋に群がる人々
• 新生活（3-4月）：引越し・入学シーズン
• GW：行楽ついでにショッピング
• 夏のボーナスセール：財布の紐が緩む時期
• ブラックフライデー：最近日本でも定着
• クリスマス商戦：プレゼント需要
• 年末年始：「今年頑張った自分へのご褒美」という魔法の言葉

これらを数式で表現してみます。

def generate_retail_sales_data(
    start_date: str = "2022-01-01",
    end_date: str = "2025-11-30",
    base_sales: float = 1000000
) -> pd.DataFrame:
    """小売店の日次売上データを生成"""

    dates = pd.date_range(start=start_date, end=end_date, freq='D')
    n_days = len(dates)

    # 1. 緩やかな成長トレンド（期間終了時に+10%）
    trend = np.linspace(0, 0.1, n_days)

    # 2. 年間季節性
    day_of_year = np.array([d.timetuple().tm_yday for d in dates])
    seasonal_yearly = (
        0.15 * np.sin(2 * np.pi * (day_of_year - 30) / 365)   # 春のピーク
        + 0.20 * np.sin(2 * np.pi * (day_of_year - 200) / 365)  # 夏セール
        + 0.15 * np.sin(2 * np.pi * (day_of_year - 340) / 365)  # 年末商戦
    )

    # 3. 週次季節性
    weekly_pattern = {
        0: -0.15,  # 月曜：みんなお疲れ
        1: -0.08,  # 火曜
        ...
        5: 0.25,   # 土曜：かき入れ時！
        6: 0.20,   # 日曜
    }

    # 4. イベント効果
    for i, date in enumerate(dates):
        if date.month == 1 and date.day <= 3:
            event_effects[i] = 0.8  # 初売り：爆売れ
        elif date.month == 12 and 20 <= date.day <= 25:
            event_effects[i] = 0.55  # クリスマス
        # ... GW、夏セール、ブラックフライデー等

    # 5. ノイズ
    noise = np.random.normal(0, 0.08, n_days)

    # 合成
    multiplier = 1 + trend + seasonal_yearly + seasonal_weekly + event_effects + noise
    sales = base_sales * multiplier

    return df

これで約1,430日分（2022/1/1 - 2025/11/30）のデータが生成されます。

ポイント: 実務では「なんでこのデータになってるの？」と聞かれることが多いです。ダミーデータでも根拠を持って作ることで、後の分析の説明がしやすくなります。

2. 前処理とEDAでデータの特徴を把握

データをそのままモデルに渡す前に、まずは内容を把握しましょう。特徴や傾向を理解しておくことで、後の分析やモデル設計がスムーズになります。

前処理としては欠損値の確認や日付・イベントからの特徴量作成などを行っていますが、本記事では詳細は割愛します。
必要に応じて、GitHub リポジトリのコードをご参照ください。

2.1 基本統計量・分布

def basic_statistics(df: pd.DataFrame, save_path: str = "figures/") -> None:
    """基本統計量の表示とヒストグラム"""
    print("📈 売上の基本統計量")
    stats = df['sales'].describe()
    print(f"\n{stats}")

    # パーセンタイル
    print(f"\n📊 パーセンタイル:")
    for p in [10, 25, 50, 75, 90, 95, 99]:
        val = df['sales'].quantile(p / 100)
        print(f"   {p}%: ¥{val:,.0f}")

結果のイメージ：

📈 売上の基本統計量
count    1.430000e+03
mean     1.175815e+06
std      2.400453e+05
min      6.112240e+05
25%      9.946942e+05
50%      1.154090e+06
75%      1.321340e+06
max      2.138889e+06
Name: sales, dtype: float64

📊 パーセンタイル:
   10%: ¥898,978
   25%: ¥994,694
   50%: ¥1,154,090
   75%: ¥1,321,340
   90%: ¥1,495,090
   95%: ¥1,622,712
   99%: ¥1,842,915

def plot_distribution(df: pd.DataFrame, save_path: str = "figures/") -> None:
    """分布の分析"""
    fig, axes = plt.subplots(2, 2, figsize=(12, 10))

    # 1. ヒストグラム
    ax1 = axes[0, 0]
    ax1.hist(df['sales'], bins=50, edgecolor='white', alpha=0.7, color='steelblue')
    ax1.axvline(df['sales'].mean(), color='red', linestyle='--', linewidth=2, label=f'平均: ¥{df["sales"].mean():,.0f}')
    ax1.axvline(df['sales'].median(), color='orange', linestyle='--', linewidth=2, label=f'中央値: ¥{df["sales"].median():,.0f}')
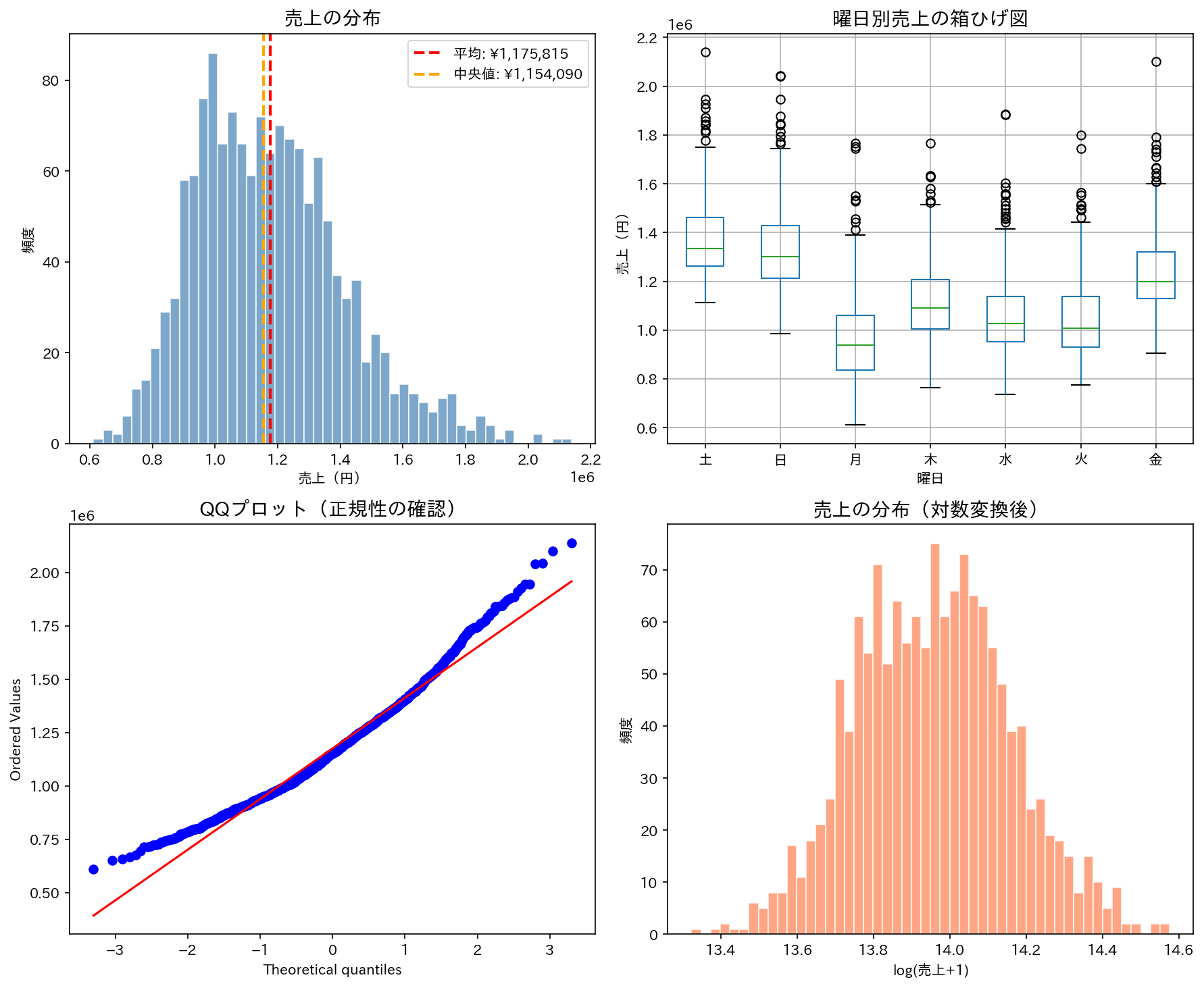
    ax1.set_title('売上の分布', fontsize=14, fontweight='bold')
    ax1.set_xlabel('売上（円）')
    ax1.set_ylabel('頻度')
    ax1.legend()

    # 2. 箱ひげ図（曜日別）
    ax2 = axes[0, 1]
    dow_names = ['月', '火', '水', '木', '金', '土', '日']
    df['dow_name'] = df['day_of_week'].map(dict(enumerate(dow_names)))
    df.boxplot(column='sales', by='dow_name', ax=ax2,
               positions=[0, 1, 2, 3, 4, 5, 6])
    ax2.set_title('曜日別売上の箱ひげ図', fontsize=14, fontweight='bold')
    ax2.set_xlabel('曜日')
    ax2.set_ylabel('売上（円）')
    plt.suptitle('')  # 自動タイトルを削除

    # 3. QQプロット（正規性の確認）
    ax3 = axes[1, 0]
    from scipy import stats
    stats.probplot(df['sales'], dist="norm", plot=ax3)
    ax3.set_title('QQプロット（正規性の確認）', fontsize=14, fontweight='bold')

    # 4. 対数変換後のヒストグラム
    ax4 = axes[1, 1]
    log_sales = np.log1p(df['sales'])
    ax4.hist(log_sales, bins=50, edgecolor='white', alpha=0.7, color='coral')
    ax4.set_title('売上の分布（対数変換後）', fontsize=14, fontweight='bold')
    ax4.set_xlabel('log(売上+1)')
    ax4.set_ylabel('頻度')

    plt.tight_layout()
    plt.savefig(f"{save_path}03_distribution.png", dpi=150, bbox_inches='tight')
    plt.close()

統計量だけでなくヒストグラムも見ておくと、売上の分布感や極端な値の影響を直感的に把握できます。
これが分かっていると、後のモデル作りがぐっとスムーズになります。

2.2 時系列プロット

def plot_time_series(df: pd.DataFrame, save_path: str = "figures/") -> None:
    """時系列プロット"""
    fig, axes = plt.subplots(3, 1, figsize=(14, 10))

    # 1. 日次売上の推移
    ax1 = axes[0]
    ax1.plot(df['date'], df['sales'], linewidth=0.8, alpha=0.7)
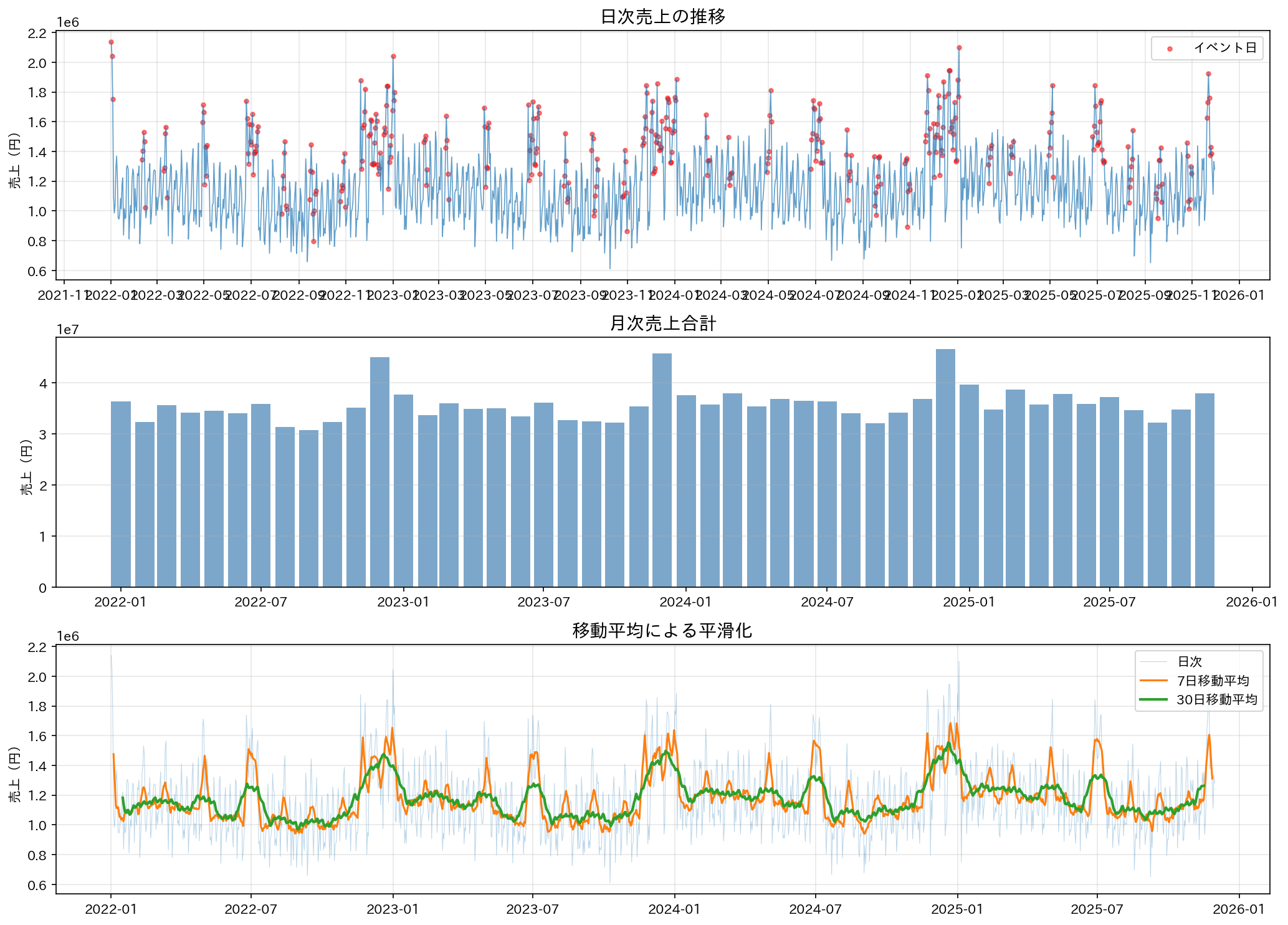
    ax1.set_title('日次売上の推移', fontsize=14, fontweight='bold')
    ax1.set_ylabel('売上（円）')
    ax1.xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))
    ax1.xaxis.set_major_locator(mdates.MonthLocator(interval=2))
    ax1.grid(True, alpha=0.3)

    # イベント期間をハイライト
    event_df = df[df['has_event'] == 1]
    ax1.scatter(event_df['date'], event_df['sales'], c='red', s=10, alpha=0.5, label='イベント日')
    ax1.legend()

    # 2. 月次売上（集計）
    ax2 = axes[1]
    monthly = df.groupby(df['date'].dt.to_period('M'))['sales'].sum()
    monthly.index = monthly.index.to_timestamp()
    ax2.bar(monthly.index, monthly.values, width=25, alpha=0.7, color='steelblue')
    ax2.set_title('月次売上合計', fontsize=14, fontweight='bold')
    ax2.set_ylabel('売上（円）')
    ax2.xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))
    ax2.grid(True, alpha=0.3, axis='y')

    # 3. 7日移動平均
    ax3 = axes[2]
    df['sales_ma7'] = df['sales'].rolling(window=7, center=True).mean()
    df['sales_ma30'] = df['sales'].rolling(window=30, center=True).mean()
    ax3.plot(df['date'], df['sales'], alpha=0.3, linewidth=0.5, label='日次')
    ax3.plot(df['date'], df['sales_ma7'], linewidth=1.5, label='7日移動平均')
    ax3.plot(df['date'], df['sales_ma30'], linewidth=2, label='30日移動平均')
    ax3.set_title('移動平均による平滑化', fontsize=14, fontweight='bold')
    ax3.set_ylabel('売上（円）')
    ax3.legend()
    ax3.grid(True, alpha=0.3)

    plt.tight_layout()
    plt.savefig(f"{save_path}01_time_series.png", dpi=150, bbox_inches='tight')
    plt.close()

発見したこと:

• 明確な年間トレンドがある（右肩上がり）
• 周期的な上下がある（週次・月次の季節性）
• 赤い点がイベント日 → 明らかに売上が高い

2.3 季節性の分析

def plot_seasonality(df: pd.DataFrame, save_path: str = "figures/") -> None:
    """季節性の分析"""
    fig, axes = plt.subplots(2, 2, figsize=(14, 10))

    # 1. 曜日別売上
    ax1 = axes[0, 0]
    dow_names = ['月', '火', '水', '木', '金', '土', '日']
    dow_sales = df.groupby('day_of_week')['sales'].mean()
    colors = ['#ff6b6b' if i >= 5 else '#4dabf7' for i in range(7)]
    ax1.bar(dow_names, dow_sales.values, color=colors)
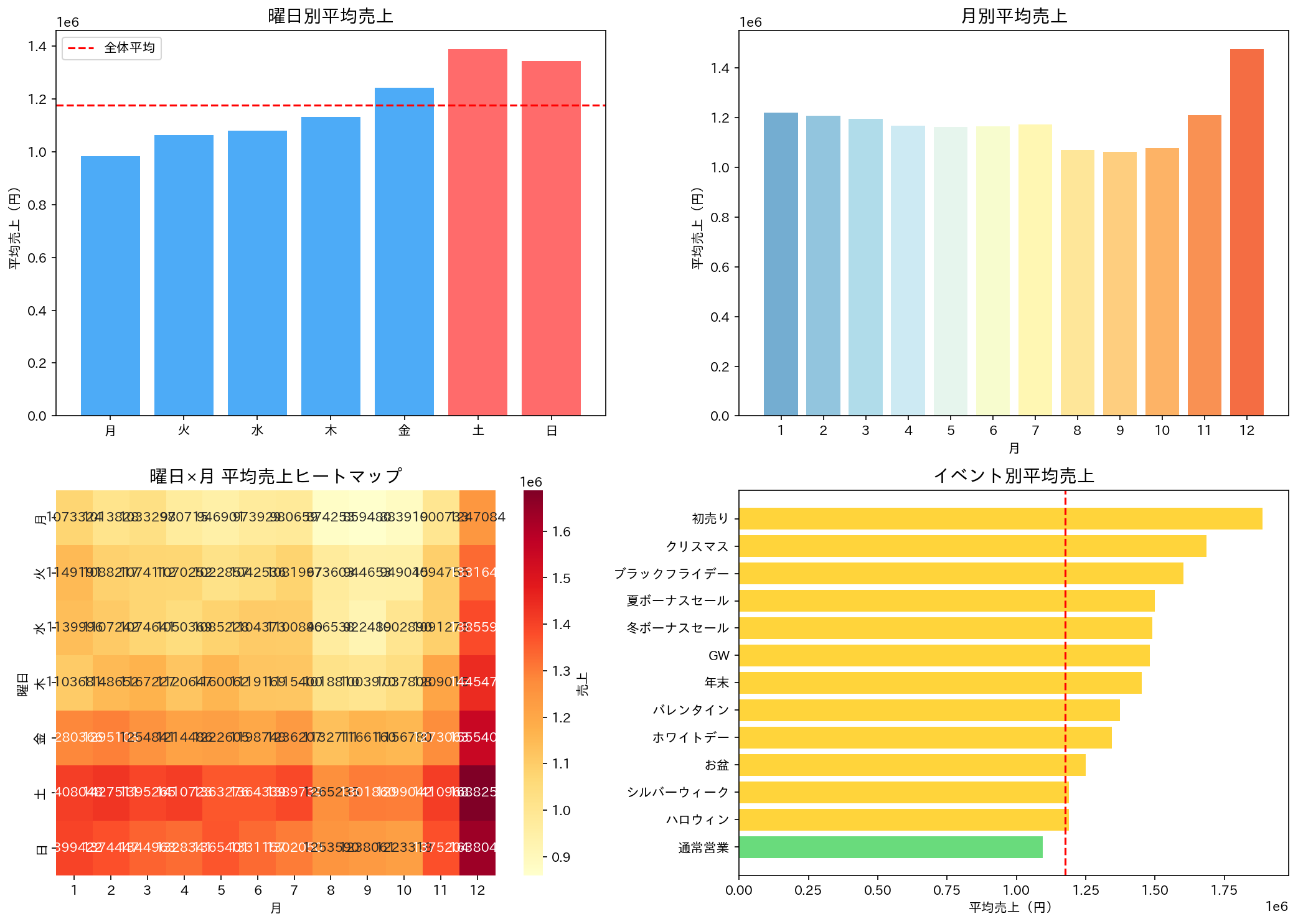
    ax1.set_title('曜日別平均売上', fontsize=14, fontweight='bold')
    ax1.set_ylabel('平均売上（円）')
    ax1.axhline(y=df['sales'].mean(), color='red', linestyle='--', label='全体平均')
    ax1.legend()

    # 2. 月別売上
    ax2 = axes[0, 1]
    month_sales = df.groupby('month')['sales'].mean()
    colors = plt.cm.RdYlBu_r(np.linspace(0.2, 0.8, 12))
    ax2.bar(range(1, 13), month_sales.values, color=colors)
    ax2.set_title('月別平均売上', fontsize=14, fontweight='bold')
    ax2.set_xlabel('月')
    ax2.set_ylabel('平均売上（円）')
    ax2.set_xticks(range(1, 13))

    # 3. 曜日×月のヒートマップ
    ax3 = axes[1, 0]
    pivot = df.pivot_table(values='sales', index='day_of_week', columns='month', aggfunc='mean')
    pivot.index = dow_names
    sns.heatmap(pivot, annot=True, fmt='.0f', cmap='YlOrRd', ax=ax3, cbar_kws={'label': '売上'})
    ax3.set_title('曜日×月 平均売上ヒートマップ', fontsize=14, fontweight='bold')
    ax3.set_xlabel('月')
    ax3.set_ylabel('曜日')

    # 4. イベント別売上
    ax4 = axes[1, 1]
    event_sales = df.groupby('event')['sales'].mean().sort_values(ascending=True)
    colors = ['#69db7c' if e == '通常営業' else '#ffd43b' for e in event_sales.index]
    ax4.barh(event_sales.index, event_sales.values, color=colors)
    ax4.set_title('イベント別平均売上', fontsize=14, fontweight='bold')
    ax4.set_xlabel('平均売上（円）')
    ax4.axvline(x=df['sales'].mean(), color='red', linestyle='--', label='全体平均')

    plt.tight_layout()
    plt.savefig(f"{save_path}02_seasonality.png", dpi=150, bbox_inches='tight')
    plt.close()

発見したこと:

• 土日は平日より**+20-25%**売上が高い
• 12月がピーク（セール時期）
• 8, 9, 10月が低い（閑散期）
• イベント開催時の売り上げが高い

ポイント: 曜日×月のヒートマップを作ると、「土曜日の12月」が最強だと分かります。逆に「月曜日の8,9,10月」は...頑張れ。

2.4 定常性の確認

時系列予測では「定常性」が重要です。ADF検定で確認します。

from statsmodels.tsa.stattools import adfuller

result = adfuller(df['sales'].dropna())
print(f"ADF統計量: {result[0]:.4f}")
print(f"p値: {result[1]:.4f}")

ADF統計量: -6.1401
p値: 0.0000

✅ p < 0.05: データは定常であると判断できます

p値が0.05未満なら定常、そうでなければ差分を取るなどの処理が必要です。

2.5 EDAの結果まとめ

【データ概要】
・期間: 2022-01-01 〜 2025-11-30
・レコード数: 1,430 件

【売上統計】
・平均売上: ¥1,175,815
・中央値: ¥1,154,090
・標準偏差: ¥240,045
・変動係数: 20.42%

【季節性の特徴】
・最も売れる曜日: 土曜日
・最も売れる月: 12月
・週末効果: +24.2%

【イベント効果】
・イベント日の売上増加率: +30.9%
・最も売れるイベント: 初売り

3. Prophetによるベースライン予測

3.1 Prophetとは

Prophetは、Facebook が開発した時系列予測ライブラリです。特徴は以下の通りです：

• 簡単: 日付と数値の列さえあれば、複雑な前処理なしで予測が可能
• 解釈しやすい: トレンド、季節性（年次・週次）、イベント効果を分解して可視化できる
• ロバスト: 欠損値や一部の異常値（アウトライア）に強く、比較的安定した予測が可能

小売業界のように「休日」や「セールなどのイベント」が売上に大きく影響するビジネスでは、Prophet を使うとその影響をモデルに反映しやすくなります。

3.2 データ準備

Prophet はデータフレームに ds（日付） と y（予測対象） のカラムがあることを期待します。
元のデータフレームから必要な列を抽出し、カラム名を変更して準備します。

prophet_df = df[['date', 'sales']].copy()
prophet_df.columns = ['ds', 'y']

これで Prophet に渡す準備は完了です。

3.3 カスタム休日の設定

ここが Prophet の強みの一つです。イベント情報を指定することで、売上の急増や減少をモデルに反映させられます。

def create_japanese_holidays() -> pd.DataFrame:
    """日本の小売に関連するイベントを定義"""
    holidays = []

    for year in [2022, 2023, 2024, 2025]:
        # 初売り
        for day in range(1, 4):
            holidays.append({
                'holiday': '初売り',
                'ds': f'{year}-01-0{day}',
                'lower_window': 0,  # 当日のみ
                'upper_window': 0,
            })

        # GW、夏ボーナス、ブラックフライデー、クリスマス...
        # （以下略）

    return pd.DataFrame(holidays)

ポイント: lower_window と upper_window で、イベントの「影響範囲」を調整できます。例えば、クリスマスの前日から影響がある場合は lower_window=-1 とします。

3.4 モデル学習

model = Prophet(
    growth='linear',                    # 線形トレンド
    seasonality_mode='multiplicative',  # 乗法的季節性（売上は比率で変動する）
    yearly_seasonality=True,
    weekly_seasonality=True,
    holidays=holidays,
    changepoint_prior_scale=0.05,       # トレンド変化点の柔軟性
    seasonality_prior_scale=10,         # 季節性の強さ
)

# 日本の祝日を追加
model.add_country_holidays(country_name='JP')

# 月次の季節性を追加
model.add_seasonality(name='monthly', period=30.5, fourier_order=5)

model.fit(train_df)

ポイント: seasonality_mode='multiplicative' は特に重要です。
売上のように「元の値に対して比率で変動するデータ」には乗法的モデルが適しています。
一方、気温のように「絶対値で変動するデータ」には加法的（additive）を選ぶのが適切です。

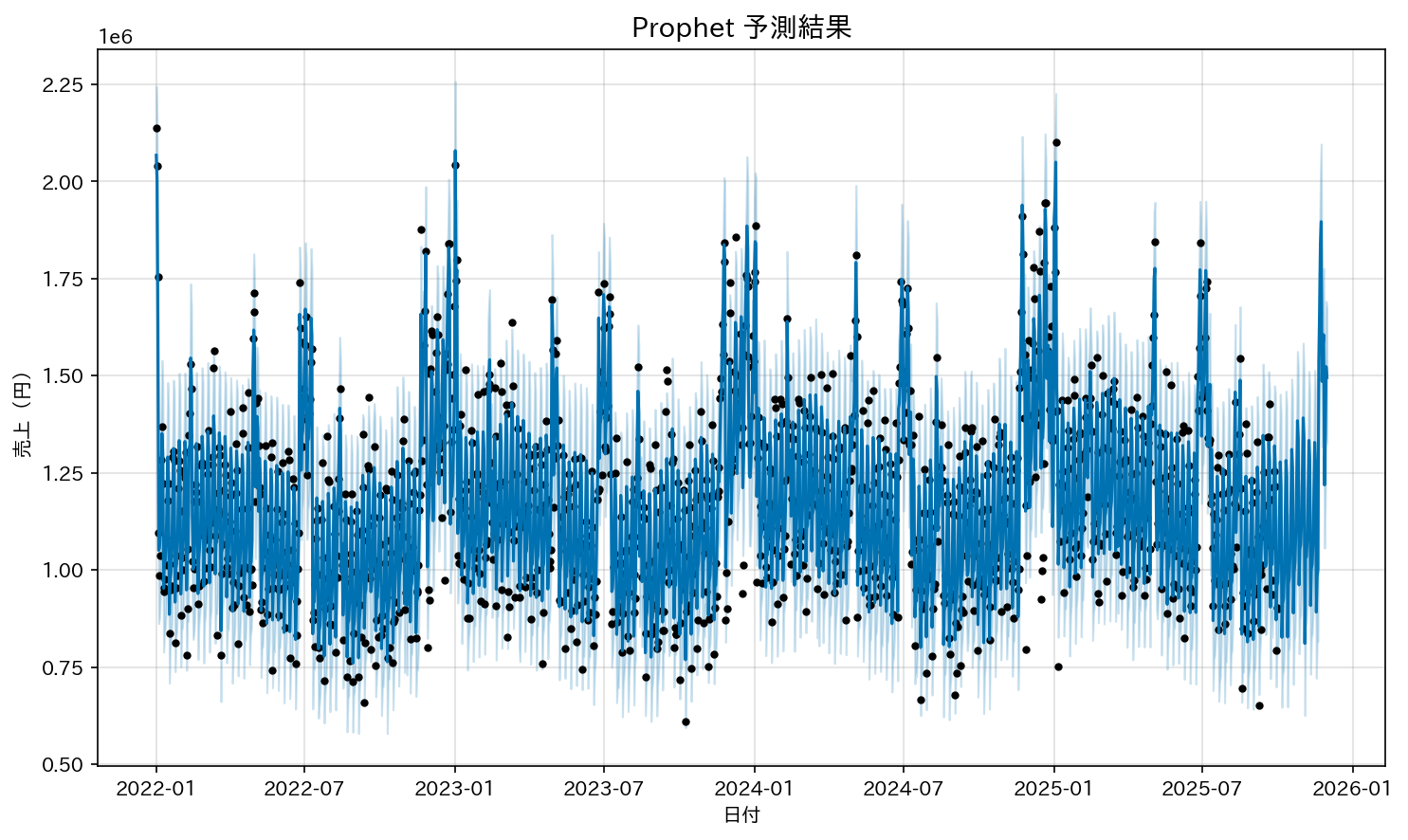
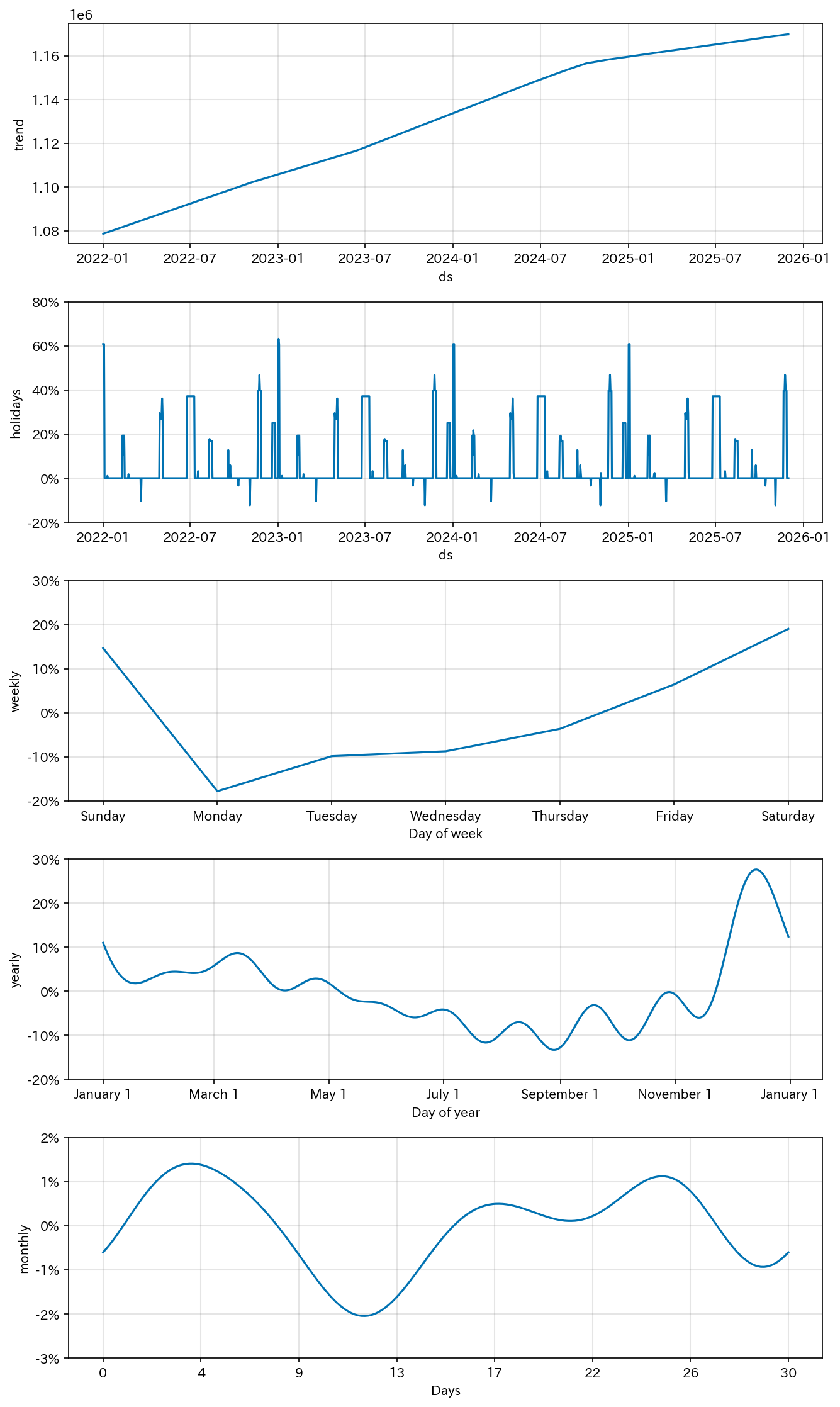
3.5 結果の可視化

予測結果と実績

成分分解

分解された成分:

• trend: 緩やかな右肩上がり
• weekly: 土日に上昇
• monthly: 5,15,25付近に波がある(給与関連?)
• yearly: 12月にピーク
• holidays: 各イベントの効果

これがProphetの強み。「なぜその予測になったか」を説明できます。

4. LightGBM + ラグ特徴量 - データリークとの戦い

4.1 時系列でGBDTモデルを使う際の最大の罠

データリーク です。

時系列データで GBDT モデルを使うときに、一番気をつけたいのが データリーク です。

普通の機械学習ならデータをシャッフルして train/test に分けますが、時系列ではそれは NG。
なぜかというと、未来の情報を使って過去を予測してしまうことになってしまうからです。

# これはダメ！
from sklearn.model_selection import train_test_split
X_train, X_test = train_test_split(df, shuffle=True)  # ← shuffle=True がNG

以下のように時間の流れを保ったまま分割します。

# 時間順に分割
split_idx = len(df) - 60  # 最後の60日をテストに
train_df = df.iloc[:split_idx]
test_df = df.iloc[split_idx:]

4.2 ラグ特徴量の作成

ラグ特徴量とは、過去のデータを特徴量として使う手法です。

def create_lag_features(
    df: pd.DataFrame,
    target_col: str = 'sales',
    lag_days: List[int] =　[1, 2, 3, 4, 5, 6, 7, 14, 21, 28]
) -> pd.DataFrame:
    df = df.copy()

    for lag in lag_days:
        df[f'lag_{lag}'] = df[target_col].shift(lag)
        print(f"   - lag_{lag}: {lag}日前の売上")

    return df

ポイント: shift(1) は「1日前の値」を持ってきます。つまり、予測時点で既に知っている値しか使っていません。
ただし、予測対象が未来に進むほど、実際の過去値は存在せず、モデルはラグ特徴量として 予測値を使うことになる 場合があります。
そのため、長期予測では精度が下がりやすいことに注意が必要です。

4.3 ローリング特徴量の罠

ここで多くの人がハマるポイントです。

# これはデータリーク！
df['rolling_mean_7'] = df['sales'].rolling(window=7).mean()

このやり方だと 当日の情報、つまり本来まだ知らない値を使ってしまうことになり、データリークにつながります。

正しくは、当日を除外してから計算することです。

# shift(1)で当日を除外してからrolling
shifted = df['sales'].shift(1)
df['rolling_mean_7'] = shifted.rolling(window=7, min_periods=1).mean()

ポイント: ローリング特徴量は過去の情報だけを使うことが重要です。
未来の値を含めてしまうと、モデルは「実際には使えない情報」で学習してしまい、見かけ上の精度は良くても実務では使えなくなります。

4.4 モデル学習

params = {
    'objective': 'regression',
    'metric': 'rmse',
    'num_leaves': 31,
    'learning_rate': 0.05,
    'feature_fraction': 0.8,
    'bagging_fraction': 0.8,
    'n_estimators': 500,
    'early_stopping_rounds': 50,
}

model = lgb.LGBMRegressor(**params)
model.fit(X_train, y_train, eval_set=[(X_val, y_val)])

ポイント:
feature_fraction や bagging_fraction で過学習を防げます。
early_stopping_rounds は学習が頭打ちになったら自動で終了してくれる便利機能です。
ハイパーパラメータは Optuna などで自動チューニングするとさらに精度を上げられますが、この記事では割愛しています。

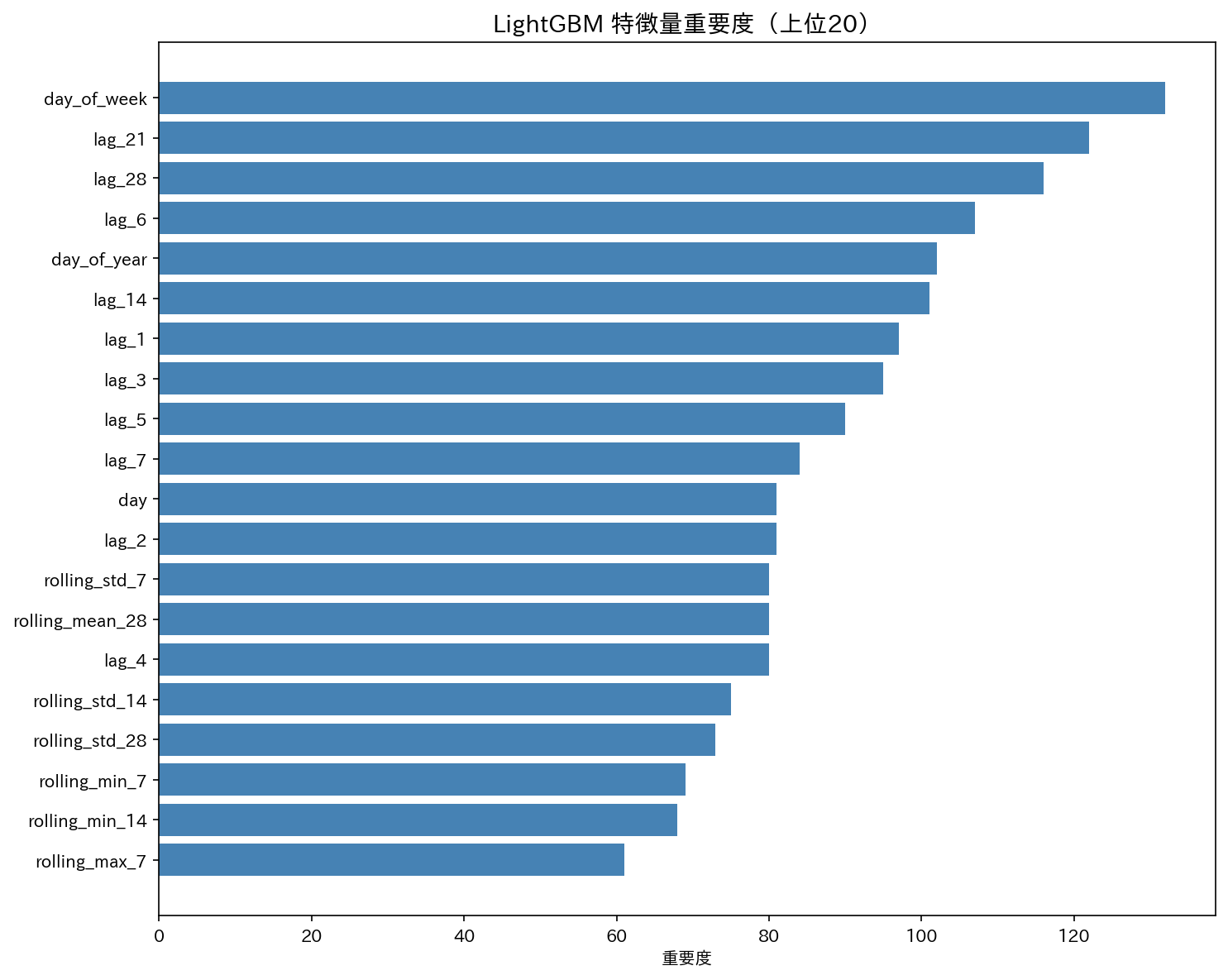
4.5 特徴量重要度

発見したこと

• 曜日（day_of_week）が最も重要
  → 週末や平日で売上が大きく変わる小売業の特性が反映されている
• lag_21, lag_28, lag_14 など、数週間前の売上が有効
  → 過去の売上パターンが短期的だけでなく、中期的にも予測に役立っている

ポイント: 特徴量重要度は「どの情報が予測に使われているか」を把握するのに便利ですが、必ずしも因果関係を示すわけではありません。
つまり「曜日が重要＝曜日を操作すれば売上が変わる」という意味ではないことに注意です。

5. 精度評価 & モデル比較

5.1 評価指標の解説

指標	意味	良い値	補足
RMSE	二乗平均平方根誤差。大きな誤差に敏感	低いほど良い	外れ値の影響を受けやすいので注意
MAE	平均絶対誤差。解釈しやすい	低いほど良い	単位が元のデータと同じなので直感的にわかる
MAPE	平均絶対パーセント誤差。スケールに依存しない	低いほど良い	予測値や実測値が0に近いと大きくぶれるため、閾値設定が必要
R²	決定係数。1に近いほど良い	高いほど良い	1に近いほどモデルがデータをよく説明しているが、過学習には注意。平均値を取るより悪いとマイナスになる

def calculate_metrics(y_true: np.ndarray, y_pred: np.ndarray) -> dict[str, float]:
    """評価指標を計算"""
    return {
        'RMSE': root_mean_squared_error(y_true, y_pred),
        'MAE': mean_absolute_error(y_true, y_pred),
        'MAPE': mean_absolute_percentage_error(y_true, y_pred),
        'R2': r2_score(y_true, y_pred)
    }

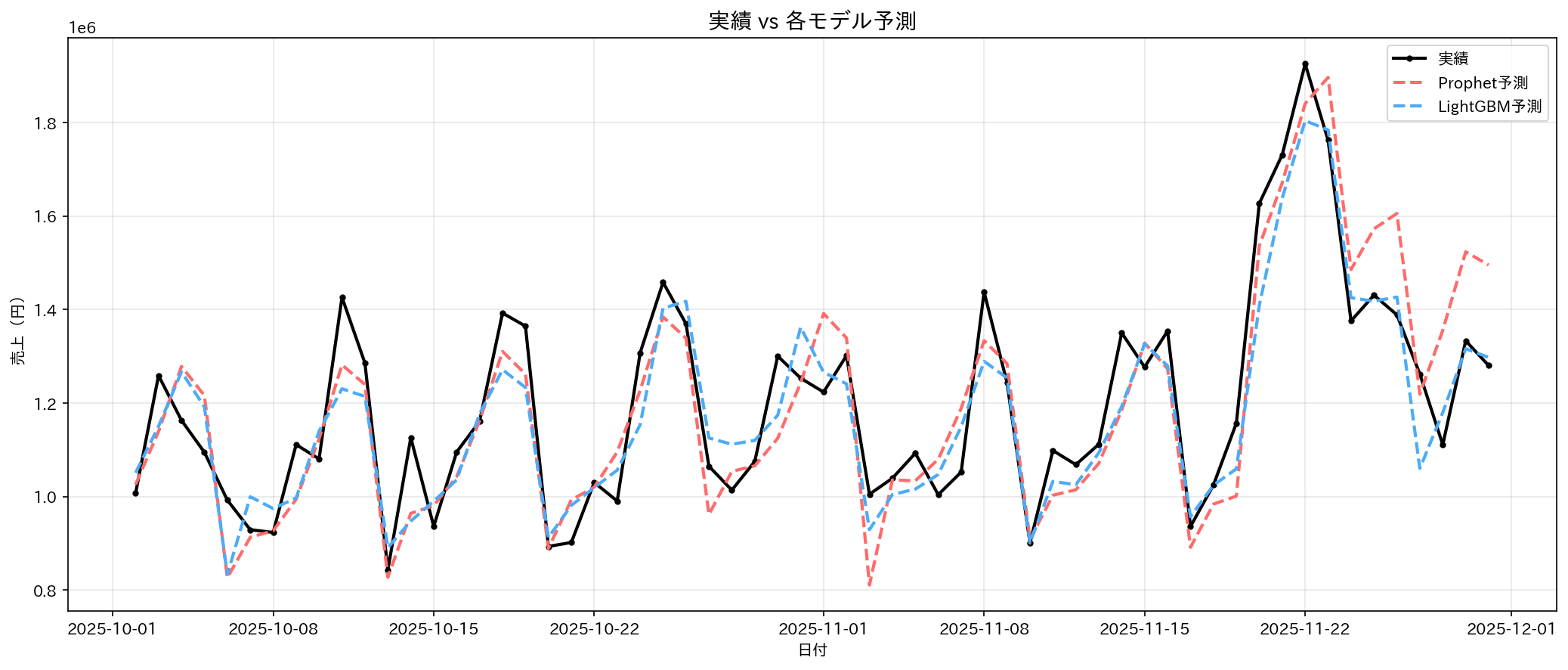
5.2 結果比較

モデル	RMSE	MAE	MAPE	R²
Prophet	¥106,410	¥86,547	7.16%	0.7732
LightGBM	¥91,766	¥75,506	6.26%	0.8313

5.3 考察

LightGBMの勝因:

• ラグ特徴量が効いた（直近の売上傾向を捉えられた）
• 柔軟な特徴量エンジニアリングが可能

Prophetの強み:

• 日付と数値データがあればモデリング可能
• 成分分解で解釈しやすい
• イベント効果の扱いが得意

どちらも強みがあります。予測の目的や精度・解釈の重視度によって使い分けが大事

6. 実務で気をつけるポイント

6.1 データリークの見つけ方

もし精度が異常に良い（R² > 0.95）場合は、要注意です。
実務のデータでは、ここまできれいに予測できることはほとんどありません。

チェック方法：

1. 特徴量重要度で「lag_0」や「当日のデータ」がトップにいないか
2. テストデータが学習データより過去になっていないか
3. ローリング計算で当日を含めていないか

ポイント: 予測精度が異常に高い場合、多くは「未来の情報を使ってしまっている」ケースです。疑ってかかりましょう。

6.2 季節性の変化

2020年、世界は一変しました。
コロナ禍によってEC需要は急増する一方で、実店舗は大打撃を受けました。

この経験から分かるのは、 「過去のパターンがそのまま通用しないことがある」 ということです。
特に季節性を前提にした予測モデルでは、例外的なイベントによって大きく外れることがあります。

変化した季節性を考慮するための工夫点：

• 最近のデータに重みを置く
  過去のデータよりも、直近のトレンドを優先して学習させる。
• 外部変数を追加する
  季節性以外の影響をモデルに組み込む。
• モデルを頻繁に更新する
  新しいデータが入るたびにモデルを更新して、変化に追従させる。
• 学習期間を調整する
  あまり古いデータまで使うとノイズになる場合があり、学習に利用する期間を適切に設定することが大事。

ポイント：過去の傾向に固執せず、「今の状況に即した柔軟な予測」が重要です。

6.3 予測区間を活用する

点予測（「来月の売上は1億円です」）だけでなく、区間予測（「1億円±1500万円」）も示すと、より現実的な判断ができます。

区間予測は「この範囲に売上が収まる可能性が高い」という目安です。
※95%信頼区間は『同じ条件で何度も予測を繰り返したら、そのうち95%の区間に真の平均が入る』範囲、とイメージするとわかりやすいです。

Prophetなら yhat_lower と yhat_upper が自動で出力されます。

forecast = model.predict(future)
print(f"予測: {forecast['yhat'].iloc[0]:,.0f}")
print(f"95%区間: {forecast['yhat_lower'].iloc[0]:,.0f} 〜 {forecast['yhat_upper'].iloc[0]:,.0f}")

6.4 未知のイベントへの対応

「来年、うちの会社が創業50周年で大セールやるんだけど…」

こういう過去にないイベントは、モデルは当然学習していません。そのまま予測すると、売上を大きく過小評価してしまう可能性があります。

対策：

• 類似イベントの効果を参考にする
  過去に似た規模のキャンペーンがあれば、その売上増加効果を参考にできます。
• 手動で効果を上乗せする
  モデル予測に人間の知見で調整を加えるのも現実的です。
• シナリオ分析を行う
  楽観・中立・悲観の3パターンで予測しておくと、リスクを含めた意思決定が可能です。

ポイント：未知のイベントはモデルだけでは予測できません。人間の知見やシナリオ設計を組み合わせることが重要です。

まとめ

今回は、小売売上の時系列予測を Prophet と LightGBM で実装しました。

前処理から精度評価まで一連のデータ分析の流れを通して、

• モデルごとの特徴
• データの傾向
• 季節性や未知イベントへの対応方法

などを理解することができました。

モデルをどう活用するかは、ドメイン知識を持った人間の判断が不可欠です。
予測はあくまで意思決定のサポートツールとして使うのがポイントです。

--

参考文献

公式ドキュメント

• Prophet公式ドキュメント
• LightGBM公式ドキュメント
• scikit-learn 評価指標

※本記事のコード・文章は一部 LLM を活用しています。