はじめに
因果推論を行う手法の1つとして、線形回帰が挙げられます。今回は、その線形回帰の拡張とも言えるリッジ回帰(Ridge回帰)やラッソ回帰(Lasso回帰)を用いて因果効果を推定してみるとどうなるのか、Pythonによるシミュレーションと共にまとめました。内容に誤り等ございましたら、ぜひご指摘いただけますと幸いです。
回帰分析を用いた因果推論については下記の記事をご参照いただけますと幸いです。
https://zenn.dev/s1ok69oo/articles/f0b91f19da2812
結論
リッジ回帰やラッソ回帰を用いると、うまく因果効果を推定することができません。
これは、リッジ回帰やラッソ回帰を行うことで、線形回帰(線形回帰モデルをOLS推定)による推定値よりも汎化誤差が小さくなる一方で、不偏性と呼ばれる因果効果をバイアスなく推定するために必要な性質が失われてしまうからです。
通常の線形回帰における最小二乗法(OLS)では、下記の損失関数を最小化するパラメータを求めます。
\sum_i(y_i - \hat{y_i})^2 \tag{1}
これによって得られた推定量が(一定の仮定のもとでは)バイアスのない推定量、すなわち、不偏推定量となります。
一方で、リッジ回帰では
\sum_i(y_i - \hat{y_i})^2 + \frac{1}{2} \lambda \sum_k \beta^2_k \tag{2}
を、ラッソ回帰では
\sum_i(y_i - \hat{y_i})^2 + \lambda \sum_k |\beta_k| \tag{3}
を損失関数とし、これらを最小化するパラメータを求めます。
リッジ回帰の損失関数(2)もラッソ回帰の損失関数(3)も、線形回帰の損失関数(1)に正則化項が足された形となっています。そのため、$\lambda \neq 0$の場合、損失関数を最小化するパラメータの値は、(1)で求められる不偏推定量とは異なってしまう(推定量にバイアスが生じてしまう)のです。
OLS推定については、下記の記事もご参照いただけますと幸いです。
https://qiita.com/s1ok69oo/items/965ccbd76df3a1628fec
Pythonによるシミュレーション
線形回帰、リッジ回帰、ラッソ回帰を用いて因果効果を推定してみます。
こちらの記事を参照し、とある大学の経済学部生120人を対象に計量経済学の特別講義(以下、特講)を開催し、その効果を推定するという設定を考えます。このとき、手元には
- 学習意欲
- 理系出身ダミー
- 特講受講ダミー
- 試験の得点
のデータがあり、特講の効果が20点、すなわち、特講を受講することで試験の得点が平均的に20点上がる、とします。
このとき、線形回帰やリッジ回帰・ラッソ回帰を用いて特講の効果(=20)を推定してみます。
機械学習タスクではしばしばパラメータのチューニングに焦点が当てられますが、今回はパラメータのチューニング等は行いません。
データの生成
Pythonで自作データを生成します。
# 必要なライブラリをインポート
import numpy as np
import pandas as pd
# シードの設定
np.random.seed(0)
# データのサイズ
size = 120
# 学習意欲を表す変数X1(交絡因子)
X1 = np.random.uniform(0, 1, size)
# 理系出身ダミーX2(交絡因子)
X2 = np.random.choice([0, 1], p=[0.5, 0.5], size=size)
# 特講受講ダミーT(処置変数)
T_noise = np.random.uniform(0, 0.2, size)
T_threshold = 0.6*X1 + 0.2*X2 + T_noise
T = np.where(T_threshold>=0.5, 1, 0)
# 試験の得点Y
Y_noise = np.random.normal(0, 15, size)
Y = np.clip(40*X1 + 20*X2 + 20*T + Y_noise, 0, 100).astype("int")
# データフレームに格納し、5つだけ出力
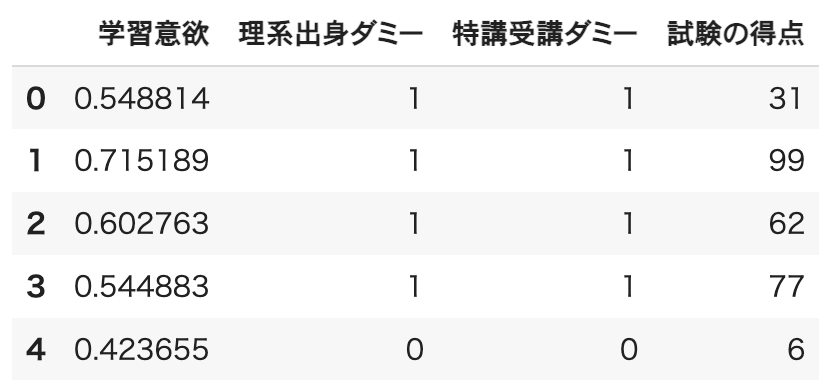
df = pd.DataFrame({"学習意欲": X1, "理系出身ダミー": X2, "特講受講ダミー": T, "試験の得点": Y})
df.head()
線形回帰による推定
線形回帰を用いて推定します。
# 必要なライブラリのインポート
from sklearn.linear_model import LinearRegression
# 説明変数
X = df[["学習意欲", "理系出身ダミー", "特講受講ダミー"]]
# 被説明変数
y = df["試験の得点"]
# モデルの設定(OLS:最小二乗法を指定)
reg_lr = LinearRegression().fit(X, y)
# 結果の詳細を表示
reg_lr.coef_[2]
(出力結果)
18.895409049029986
特講の効果は20であるため、それなりによく推定できているようです。
リッジ回帰による推定
リッジ回帰を用いて推定します。
# 必要なライブラリのインポート
from sklearn.linear_model import Ridge
# 説明変数
X = df[["学習意欲", "理系出身ダミー", "特講受講ダミー"]]
# 被説明変数
y = df["試験の得点"]
# モデルの設定(OLS:最小二乗法を指定)
reg_ridge = Ridge().fit(X, y)
# 結果の詳細を表示
reg_ridge.coef_[2]
(出力結果)
22.14323714116598
若干ではありますが、線形回帰の方がバイアスなく推定できているようです。
ラッソ回帰による推定
ラッソ回帰を用いて推定します。
# 必要なライブラリのインポート
from sklearn.linear_model import Lasso
# 説明変数
X = df[["学習意欲", "理系出身ダミー", "特講受講ダミー"]]
# 被説明変数
y = df["試験の得点"]
# モデルの設定(OLS:最小二乗法を指定)
reg_lasso = Lasso().fit(X, y)
# 結果の詳細を表示
reg_lasso.coef_[2]
(出力結果)
27.78978079808095
こちらはかなり推定値にバイアスが生じているようです。
線形回帰モデルは説明変数が増えると過学習してしまう傾向にありますが、この過学習を抑えられることがリッジ回帰やラッソ回帰を用いる利点になります。そのため、そもそも今回のように説明変数が少ないテーマでリッジ回帰やラッソ回帰を用いること自体があまり適切ではなかったかもしれません。
おまけ(Meta-Learnerによる比較)
近年では、機械学習と因果推論を掛け合わせたアプローチも研究されており、その1つにMeta-Learnerと呼ばれる手法があります。そのMeta-Learnerを用いて、機械学習モデルに線形回帰・リッジ回帰・ラッソ回帰の各々を利用した場合の効果の推定値を確認してみます。
Meta-LearnerはCATEを推定する際にも有効であり、非線形の効果を捉える点が魅力の1つです。そのため、機械学習モデルに線形回帰を使うことはあまりない印象です。Meta-Learnerについては下記の記事もご参照いただけますと幸いです。
https://zenn.dev/s1ok69oo/articles/1eeebe75842a50
T-Learner
Meta-Learnerの手法の1つである、T-Learnerを用いて効果を推定します。
T-Learnerのイメージは下記の通りです。
- 処置が行われた(特攻を受講した)グループのデータを用いて、処置が行われた場合の予測モデル$M_1$を作成
- 処置が行われていない(特攻を受講していない)グループのデータを用いて、処置が行われていない場合の予測モデル$M_0$を作成
- 2つの予測モデル$M_1, M_0$を用いて、$M_1(X=x)-M_0(X=x)$として効果を推定
この2つの予測モデル$M_1, M_0$に、線形回帰・リッジ回帰・ラッソ回帰を利用してみます。この場合「線形回帰よりもリッジ回帰やラッソ回帰の方が予測精度が高い場合には、リッジ回帰やラッソ回帰の方が効果をバイアスなく推定できるのではないか?」という思惑です。
こちらはあくまでも仮説です。もし詳しい方がいらっしゃいましたら、コメントいただけますと幸いです。
「線形回帰よりもリッジ回帰やラッソ回帰の方が予測精度が高い場合には、リッジ回帰やラッソ回帰の方が効果をバイアスなく推定できるのではないか?」
T-Learner×線形回帰
# 必要なライブラリのインポート
from econml.metalearners import TLearner
# 説明変数
x = df[["学習意欲", "理系出身ダミー"]]
# 被説明変数
Y = df["試験の得点"]
# 処置変数
T = df["特講受講ダミー"]
# モデルの構築
reg_lr = LinearRegression()
T_learner = TLearner(models=reg_lr)
T_learner.fit(Y, T, X=x)
# 平均的な効果を出力
tau = T_learner.effect(x)
tau.mean()
(出力結果)
17.90413176363971
本来の効果は20であるため、推定値に少しバイアスがあるようです。
T-Learner×リッジ回帰
# 必要なライブラリのインポート
from econml.metalearners import TLearner
# 説明変数
x = df[["学習意欲", "理系出身ダミー"]]
# 被説明変数
Y = df["試験の得点"]
# 処置変数
T = df["特講受講ダミー"]
# モデルの構築
reg_ridge = Ridge()
T_learner = TLearner(models=reg_ridge)
T_learner.fit(Y, T, X=x)
# 平均的な効果を出力
tau = T_learner.effect(x)
tau.mean()
(出力結果)
27.505411986681352
T-Learner×線形回帰よりも推定値のバイアスが大きくなりました。
T-Learner×ラッソ回帰
# 必要なライブラリのインポート
from econml.metalearners import TLearner
# 説明変数
x = df[["学習意欲", "理系出身ダミー"]]
# 被説明変数
Y = df["試験の得点"]
# 処置変数
T = df["特講受講ダミー"]
# モデルの構築
reg_lasso = Lasso()
T_learner = TLearner(models=reg_lasso)
T_learner.fit(Y, T, X=x)
# 平均的な効果を出力
tau = T_learner.effect(x)
tau.mean()
(出力結果)
41.53565595483376
こちらもリッジ回帰と同様に、T-Learner×線形回帰よりも推定値のバイアスが大きくなりました。
補足
今回のケースでは(少しモデルが異なってしまいますが)訓練データとテストデータに分割し、汎化誤差を計算してみても下記の通りであったため、当初の思惑であった「線形回帰よりもリッジ回帰やラッソ回帰の方が予測精度が高い場合には、リッジ回帰やラッソ回帰の方が効果をバイアスなく推定できるのではないか?」という仮説は検証できなかったようです。
# 必要なライブラリのインポート
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# モデルの構築
reg_lr = LinearRegression().fit(X_train, y_train)
reg_ridge = Ridge().fit(X_train, y_train)
reg_lasso = Lasso().fit(X_train, y_train)
# 予測
y_pred_lr = reg_lr.predict(X_test)
y_pred_ridge = reg_ridge.predict(X_test)
y_pred_lasso = reg_lasso.predict(X_test)
# 汎化誤差の計算
mse_lr = mean_squared_error(y_test, y_pred_lr)
mse_ridge = mean_squared_error(y_test, y_pred_ridge)
mse_lasso = mean_squared_error(y_test, y_pred_lasso)
# 汎化誤差の出力
print(f"線形回帰の汎化誤差: {mse_lr}")
print(f"リッジ回帰の汎化誤差: {mse_ridge}")
print(f"ラッソ回帰の汎化誤差: {mse_lasso}")
(出力結果)
線形回帰の汎化誤差: 123.66865922818248
リッジ回帰の汎化誤差: 123.44640473443128
ラッソ回帰の汎化誤差: 142.78430938017732
おわりに
最後まで読んでいただきありがとうございました。
zennにて「Python×データ分析」をメインテーマに記事を執筆しているので、ご一読いただけますと幸いです。
また、過去にLTや勉強会で発表した資料が下記リンクにてまとめてありますので、こちらもぜひご一読くださいませ。
参考文献
Web上の資料は2023年3月8日時点のものです。