はじめに
データ分析の現場で特に断りなく"回帰分析"と表現する場合は、線形モデルを仮定して回帰直線を求める線形回帰を指していることが多いと思います。そして「回帰分析をしてください」と言われると、とりあえず「RやPythonのパッケージを利用して、最小二乗法(以下、OLS: Ordinary Learst Squares)で推定値を求める」というケースが多い印象です。
しかし、「なぜOLSを使うのか?」「本当に最小二乗推定量(以下、OLS推定量)が"良い"推定値なのか?」と聞かれると、言葉に詰まるというシーンも少なくないかと思います。
そこで今回は、
- OLS推定量の特性
- OLSのアンチパターンと代表的な対処方法
についてまとめました。
内容について誤り等ございましたら、コメントにてご指摘いただけますと幸いです。
OLS推定量の特性
単回帰モデルをベースに、OLSの仕組みやOLS推定量を用いる上で必要な仮定や押さえておくべき性質についてご紹介します。
OLSの仕組み
直感的な理解のために、以下のようなモデルを考えます。
$$Y_i = \beta_0 + \beta_1 X_i + u_i \tag{a}$$
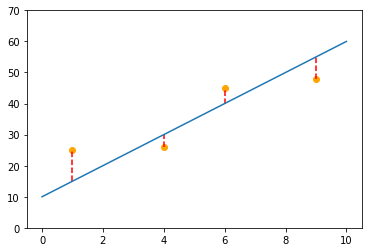
(a)式を図で表すとこのようになります。
OLSでは、直線と各プロットまでの縦方向の距離(赤の破線部: 誤差$u_i$)の総和が最小になるように回帰直線を引くことを考えます。「誤差が小さい=よく推定できている」という考え方は直感的にも納得しやすいかと思います。
ただし、誤差$u_i$の総和をそのまま考えてしまうと、$\sum_i |u_i|$と絶対値を含んだ式を考える必要があり何かと面倒です。そのため、「誤差$u_i$の二乗和を最小にする問題を解くことで、誤差$u_i$の総和を最小とするパラメータ$\beta_0, \beta_1$を推定する」というアプローチがOLSの考え方になります。
「誤差$u_i$の二乗和を最小にする問題」は
\sum_i {u_i}^2=\sum_i \{Y_i - (\beta_0 + \beta_1 X_i) \}^2
を$\beta_0, \beta_1$で偏微分したものがゼロになるような条件を求めればよく、$\bar{X}, \bar{Y}$を$X,Y$の標本平均として
$$\hat{\beta_1} = \frac{\sum_i{(X_i - \bar{X})(Y_i - \bar{Y})}}{\sum_i{(X_i - \bar{X})^2}}, \ \hat{\beta_0} = \bar{Y} - \hat{\beta_1}\bar{X}$$
と表され、OLSによって推定されたパラメータや標準誤差はOLS推定量と呼ばれます。
OLSが用いられる理由
単回帰モデルが次の3つの仮定を満たすとき、OLS推定量は「望ましい」性質(後述)を持つことが知られています。
単回帰モデルの仮定
- データ$(Y_i, X_i)$は独立で同一な分布に従い(i.i.d)、かつ次の関係を満たす。$$Y_i = \beta_0 + \beta_1 X_i + u_i$$
- 説明変数で条件づけた誤差項の期待値は0である$$E(u_i|X_i)=0$$
- $X_i$と$u_i$の4次モーメントが有限である$$0 < E(X^4_i)<\infty, \ 0 < E(u^4_i)<\infty$$
(1)の仮定は、$(X_1, Y_1), ..., (X_n, Y_n)$が同一の母集団から無作為標本されていれば満たされるものです。このとき、誤差項間は相関を持たず、$$Cov(u_i, u_j)=0 \ (i \neq j) \tag{b}$$が成り立ちます。
(2)の仮定は、外生性と呼ばれ、$X_i$以外の$Y_i$の決定要因(すなわち、誤差項$u_i$)は、OLS推定量の不偏性や一致性(後述)を持つために重要な仮定になります。(2)の仮定の代わりに、$X_i$と$u_i$が無相関、すなわち、$$Cov(X_i, u_i) = 0 \tag{c}$$あるいは、$$X_i \ と \ u_i \ は独立 \tag{d}$$という仮定がなされる場合もあり、(d)式が正しければ(2)式が成り立ち、(2)式が正しければ(c)式が成り立つということが知られています。
(3)の仮定は、漸近正規性を示すために必要になるものですが、直感的には「正規近似ができないほど頻繁に異常値を取らないことを保証する仮定」という理解で良いと思います。
重回帰モデルの場合は、以下のような仮定を満たすときにOLS推定量は「望ましい」性質を持つことが知られています。
- i.i.d: $(Y_i, X_{1i}, ..., X_{ki})$は独立同一分布に従う
- 外生性: $E(u_i|X_{1i}, ..., X_{ki})=0$が成り立つ
- 異常値を取らない: $(X_{1i}, ..., X_{ki}, u_i)$は4次までのモーメントを持つ
- 多重共線性がない: 任意の$\ \sum_j a^2_j = 1 \ $となる$\ a_0, ..., a_k \ $について、$E[(a_0 + a_1 X_{1i} + ... + a_k X_{ki})^2] > 0$が成り立つ
OLS推定量が持つ3つの「望ましい」性質
- 不偏性: 推定量の期待値が真の値に等しいという性質で、推定量に誤差があっても平均すれば真の値になることを意味します。$$E(\hat{\beta_1}) = \beta_1$$
- 一致性: サンプルサイズを大きくすれば推定量がある値に収束するという性質です。一致性がないと、サンプルサイズをいくら増やしても推定量が収束せず、推定結果が信頼できかねるものとなってしまいます。$$\hat{\beta_1} \xrightarrow{p} \beta_1$$
- 漸近正規性: サンプルサイズが大きいとき、そのサンプルから構成されるある確率変数が近似的に正規分布を従うという性質です。漸近正規性自体は、直接的に推定量の良し悪しに関わる性質ではありませんが、係数に関する仮設検定や区間推定を行う際に非常に重要な性質となっています。$$\sqrt{n}(\hat{\beta_1} - \beta_1) \xrightarrow{d} N \Big( 0, \frac{Var[(X_i - E[X_i])u_i]}{Var[X_i]^2} \Big)$$
これだけでも十分に魅力的な推定量ではありますが、さらに「均一分散」と呼ばれる仮定を置くことによって、OLS推定量はBLUEと呼ばれる「最も適切な推定量」になることが知られています。
均一分散とは
誤差項の分散が説明変数の値と関係なく一定の値$\ \sigma^2 $である、すなわち、$X_i$における$u_i$の条件付き分散が$\sigma^2$であるとき「均一分散である」といい、$$Var(u_i|X_i) = E(u^2_i|X_i) = \sigma^2$$が成り立ちます。逆に、$Var(u_i|X_i) \ $が$X_i$に依存する($X_i$の関数として表される)とき「不均一分散である」といいます。
均一分散が成り立たない(不均一分散)のケースを直感的に理解できる例としては「所得の多寡」の「消費支出」の関係が挙げられます。例えば、年間の所得が300万円の世帯であれば、年間の消費支出額は0~300万円の範囲で散らばるはずです。それに対して年間の所得が1,000万円の世帯であれば、年間の消費支出額は0~1,000万円の範囲で散らばると考えられます。この場合、所得が年300万円の世帯と年1,000万円の世帯の分散が同じとは考えづらく、均一分散が成り立っていないと考えるのが自然です。
BLUEとは
BLUEとは「Best Linear Unbiased Estimator」の略で、最良線形不偏推定量とも呼ばれます。BLUEには4つの特性があります。
- 線形性: 線形モデルの推定量であることを意味します。
- 不偏性: 推定量の期待値が真の値に等しいという性質で、推定量に誤差があっても平均すれば真の値になることを意味します。
- 効率性: 推定量の分散が最小であることを意味し、有効性とも呼ばれます。
- 一致性: サンプルサイズを大きくすれば推定量がある値に収束するという性質です。一致性がないと、サンプルサイズをいくら増やしても推定量が収束せず、推定結果が信頼できかねるものとなってしまいます。
単回帰モデル(あるいは、重回帰モデル)の仮定に加えて、均一分散が成り立つとき、OLS推定量がBLUEになるという性質を「ガウス=マルコフの定理」と言います。
OLSのアンチパターンと代表的な対処方法
OLS推定量は、ときにBLUE(最もベストな推定量)になると説明しましたが、現実的にはBLUEとなるケースは多くありません。そこでOLS推定量がBLUEとならないケースを本記事における「OLSのアンチパターン」として紹介させていただきます。
均一分散が成立しないケース(不均一分散)
均一分散とは、$X_i$における$u_i$の条件付き分散が一定の値$\sigma^2$である、すなわち、$$Var(u_i|X_i) = E(u^2_i|X_i) = \sigma^2$$が成り立つという性質でした。均一分散が成立しないケースとして、先ほど紹介した「所得の多寡」と「消費支出」の関係の他に、平均値データを取り扱うというケースが挙げられます。
例えば、都道府県別の平均的な消費支出のバラツキを考える際には、世帯単位の消費の分散を$\sigma^2$、世帯数を$N_i$とおくと、都道府県別の消費の平均の分散は$\frac{\sigma^2}{N_i}$と表されます。これは世帯数$N_i$が大きいほど、平均の分散が小さくなる性質を表しており、世帯数$N_i$が都道府県別で異なると、均一分散が成り立たないことを示しています。
均一分散が成り立たない場合、OLS推定量の効率性がなくなってしまいます。このようなケースでは次の2つの対処法が挙げられます。
対処法1: 不均一分散に対して頑健な標準誤差
OLSを用いて推定量の標準誤差を算出する際に、不均一分散が生じている可能性を考慮した「不均一分散に対して頑健な標準誤差」を利用するという方法です。不均一分散に対して頑健な標準誤差はいくつか考案されていますが、中でも代表的なものがホワイトの標準誤差で、下記のように表されます。
$$SE(\hat{\beta_0}) = \sqrt{\frac{\hat{V_0}}{N}}, \ SE(\hat{\beta_1}) = \sqrt{\frac{\hat{V_1}}{N}}$$ただし、
H_i = 1 - \Big( \frac{\bar{X}}{\frac{1}{N}\sum_j X^2_j} \Big)X_i,
\ \hat{V_0} = \frac{\frac{1}{N} \sum_i \hat{H_i}^2 \hat{u_i}^2}{ \Big( \frac{1}{N}\sum_i \hat{H_i}^2 \Big)^2},
\ \hat{V_1} = \frac{\frac{1}{N} \sum_i(X_i - \bar{X})^2 \hat{u_i}^2}{\Big\{ \frac{1}{N} \sum_i(X_i - \bar{X})^2 \Big\}^2 }
推定式自体は少し複雑ですが、多くの統計ソフトでオプションを指定するだけで簡単に利用することができるため、頻繁に用いられるイメージです。
対処法2: 一般化最小二乗法
先ほどの都道府県別平均値データのように、不均一分散の構造が分かっている場合、一般化最小二乗法(以下、GLS: Generalized Least Square)という手法を用いてバイアスを除去した推定が可能となるケースがあります。
GLSとは、被説明変数$Y_i$と説明変数$X_i$を何らかの形に変換した$Y'$と$X'$をOLSで推定する方法です。
先ほどの例では、都道府県別の消費の平均の分散は$\frac{\sigma^2}{N_i}$と表されていました。そのため、元の推定式の両辺に$\sqrt{N_i}$をかけることによって、分散の分母$N_i$を消してあげます。元の推定式を$$Y_i = \beta_0 + \beta_1 X_i + u_i$$とすると、両辺に$\sqrt{N_i}$をかけて$$\sqrt{N_i}Y_i = \beta_0 \sqrt{N_i} + \beta_1 \sqrt{N_i} X_i + \sqrt{N_i} u_i$$とし、$\sqrt{N_i}Y_i, \sqrt{N_i} X_i$を$Y', X'$と変換して$\beta_1$についてOLS推定します。
上記の例は、GLSの特殊形であり、加重最小二乗法(WLS: Weighted Least Square)と呼ばれています。
仮定(1)が成立しないケース
仮定(1)とは、データ$(Y_i, X_i)$は独立で同一な分布に従い(i.i.d)、かつ次の関係を満たす、すなわち、$$Y_i = \beta_0 + \beta_1 X_i + u_i$$というものでした。
しかし、時系列データやパネルデータでは「独立」という仮定を満たさないことが多いです。例えば、家計の消費支出には慣性効果というものがあり、一度消費支出を大きくしてしまうと翌年も消費水準が大きくなったまま変えられないorもっと大きくしてしまうと言われています。
仮定(1)が成立しない場合もOLS推定量の効率性がなくなってしまいます。このようなケースについて、次の2つの対処法をご紹介します。
対処法1: コクラン・オーカット法
推定したいパラメータは単回帰モデル$$Y_t = \beta_0 + \beta_1 X_t + u_t \tag{e}$$の$\beta_1$であるとし、このとき誤差項$u_i$は$$u_t = \rho u_{t-1} + v_t \tag{f}$$と表されるとします。ここで$\rho$は自己相関係数を表し、$-1 < \rho < 1$を満たすと仮定します。ここで(f)式を用いると(e)式は$$Y_t - \rho Y_{t-1} = (1 - \rho)\beta_0 +\beta_1 (X_t - \rho X_{t-1}) + v_t \tag{g}$$と変換することができます。
ただし、$\rho$は未知であるため、まずは(e)式をOLS推定し、その残差を用いて自己回帰モデル(f)式をOLS推定することで$\hat{\rho}$を求める必要があります。そして、最後に(g)式の$\rho$を$\hat{\rho}$に置き換えて、$\beta_1$をOLS推定します。
対処法2: 変量効果モデル
パネルデータを用いた推定式は、以下のように経済主体iと時点tの2つの添字を明示するのが一般的です。$$Y_{it} = \beta_0 + \beta_1 X_{it} + u_{it}$$ここで、誤差項$u_{it}$を時間によって変わらない経済主体に固有な要素$F_i$(固有効果)と、それ以外の要素$v_{it}$に分解します。$$Y_{it} = \beta_0 + \beta_1 X_{it} + (F_i + v_{it}) \tag{h}$$この際、固有効果$F_i$と説明変数$X_{it}$が独立であるとき、(h)式は変量効果モデルと言われます。変量効果モデルでは、固有効果$F_i$によって常に大きな誤差を持つため、この誤差間の相関の構造をあらかじめ考慮し、GLS推定を行います。
仮定(2)が成立しないケース
仮定(2)とは、説明変数で条件づけた誤差項の期待値は0である、すなわち、$$E(u_i|X_i)=0$$というものでした。こちらの仮定が満たされるには少なくとも説明変数$X_i$は誤差項$u_i$と無相関でなければいけないことが知られています。逆に言うと、説明変数$X_i$と誤差項$u_i$の間に相関があれば、仮定(2)は成立しません。
このようなケースで有名なもの欠落変数があるケースが考えられます。欠落変数とは、本来ならば説明変数に含まれるべき変数、具体的には「被説明変数の決定要因のうち、他の説明変数と相関がある変数」のことを指します。欠落変数$M_i$があると、説明変数$X_i$と誤差項$u_i$に相関が生じてしまい、推定量が真の値から外れてしまいます(欠落変数バイアス)。
説明変数$X_i$と誤差項$u_i$に相関が生まれるメカニズムとしては、欠落変数$M_i$は被説明変数$Y_i$の決定要因の1つなので、$$Y_i = \beta_0 + \beta_1 X_i+ \beta_2 M_i + v_i$$と表されます。このとき、変数$M_i$を説明変数に含めずOLS推定してしまうと、表面的にはモデルを$$Y_i = \beta_0 + \beta_1 X_i + u_i$$と置いていることになります。しかし、実態としては含めなかった変数$M_i$は誤差項$u_i(= \beta_2 M_i + v_i)$の中に含まれています。そのため、説明変数$X_i$と欠落変数$M_i$に相関があると、結果として説明変数$X_i$と誤差項$u_i$にも相関が生じてしまうのです。
他にも、説明変数$X_i$が外生変数ではなく内生変数である場合にも、説明変数$X_i$と誤差項$u_i$の間に相関が生じてしまいます(定義です)。
$X_i$が内生変数の場合、逆の因果が生じている($Y_i$によって$X_i$が説明される)ケースや同時決定(説明変数と被説明変数がお互いに影響し合っている)ケースが考えられます。
仮定(2)が成立しない場合、OLS推定量が一致性を満たさなくなってしまうため、推定上の問題としては深刻です。各々のケースについて、次のような対処法があります。
欠落変数に対する対処法: 固定効果モデル
固定効果モデルでは、変量効果モデルと同様に$$Y_{it} = \beta_0 + \beta_1 X_{it} + u_{it}$$ここで、誤差項$u_{it}$を時間によって変わらない経済主体に固有な要素$F_i$(固有効果)と、それ以外の要素$v_{it}$に分解します。$$Y_{it} = \beta_0 + \beta_1 X_{it} + (F_i + v_{it})$$変量効果モデルと違う点は、固有効果$F_i$と説明変数$X_{it}$に相関があることを想定する点です。
欠落変数$M_i$が存在している場合には、固有効果$F_i$を欠落変数$M_i$に見立てて推定するというイメージです。
固定効果モデルによる推定では、期間平均値との差分を考えます。$$Y_{it} = \beta_1 X_{it} + F_i + v_{it}$$という式($\beta_0$も固有効果$F_i$に含めてしまっています)から、期間平均値$$\bar{Y_i} = \beta_1 \bar{X_i} + F_i + \bar{v_i}$$の差をとると$$Y_{it} - \bar{Y_i} = \beta_1 (X_{it} - \bar{X_i}) + (F_i - F_i) + (v_{it} - \bar{v_i})$$すなわち$$\tilde{Y_{it}} = \beta_1 \tilde{X_{it}} + \tilde{v_{it}}$$と表すことができます。このように差分をとることで固有効果$F_i$を除去し、最後に$\tilde{Y_{it}}, \tilde{X_{it}}$を用いた推定式をOLSで推定します。
内生変数に対する対処法: 操作変数法
内生変数が存在する(かもしれない)場合にも適切な操作変数を用いることによって一致性のある推定量を求めることができます。内生変数と操作変数がともにひとつずつの場合、適切な操作変数$Z_i$の条件は
- 説明変数$X_i$に影響を与える: $Cov(Z_i, X_i) \neq 0$
- 被説明変数$Y_i$からの影響は直接受けない: $Cov(Z_i, u_i)=0$
となります。上記を満たす操作変数$Z_i$を利用することで、$$\hat{\beta_1} = \frac{\sum_i (Z_i - \bar{Z})(Y_i - \bar{Y})}{\sum_i (Z_i - \bar{Z})(X_i - \bar{X})}$$と推定することができます。
おわりに
最後まで読んでいただきありがとうございました。
zennにて「Python×データ分析」をメインテーマに記事を執筆しているので、ご一読いただけますと幸いです。
また、過去にLTや勉強会で発表した資料が下記リンクにてまとめてありますので、こちらもぜひご一読くださいませ。
参考文献
- 久保川(2017)「現代数理統計学の基礎」共立出版
- 末石(2015)「計量経済学」日本評論社
- 田中(2019)「計量経済学のための数学」日本評論社
- 東京大学教養学部統計学教室(1991)「統計学入門」東京大学出版会
- 西山他(2019)「計量経済学」有斐閣
- 山本(2015)「実証分析のための計量経済学」中央経済社