関係演算アルゴリズムとコスト
前回 -> https://qiita.com/s0t00524/items/a4f57f7568f2784464a0
この記事は大学の期末試験勉強のために作成したものです。間違い等は悪しからず。
関係データベース演算の種類
- 入力演算
- 選択(Selection)
- 射影([Delta] Projection)
- 集約(Aggregation)
- 整列(Order-By)
- 重複除去(Duplication Elimination)
- グループ化(Group-By)
- 結合(Join)
- 準結合(Semi-Join)
- 集合積(Intersection)
- 集合差(Difference)
- 集合和(Union)
- 直積(Cartesian Product)
- 商(Division)
演算のコスト見積もり
比較回数(CPUコスト)とディスクI/Oによって見積もる。また以下の議論では、関係代数Rのサイズを以下で定義する。
- Rのタプル数:$\{R\}$
- Rのディスクページ数:$|R|$
各選択演算とコストの見積もり
GRACEハッシュ結合とそのコスト
分散フェーズと結合フェーズの各フェーズで独立のハッシュ関数を使用。合計で2個使う。
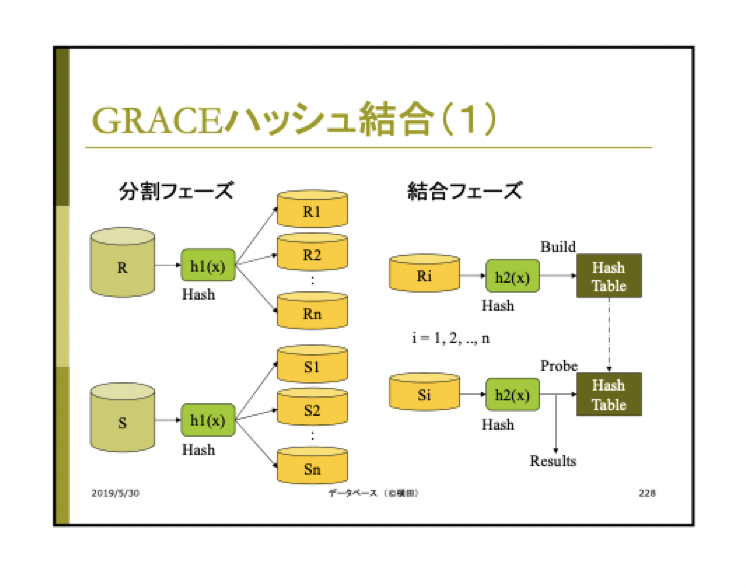
-
ハッシュ適用回数:$2(\{R\} + \{S\})$
- 各フェーズで$\{R\} + \{S\}$
-
比較回数:$\sum\{S_i\} = (\{S\}/n) \times n = \{S\}$
-
ディスクI/O回数:$3(|R|+|S|)$
ハイブリッドハッシュ結合

- 比較回数とハッシュ適用回数:GRACEと同じ
- ディスクI/O回数:$3(|R|+|S|) - 2(|R|+|S|)/L = (3 - 2|M|/|R|) \times (|R|+|S|)$
メモリ不足の場合の三種類のハッシュ結合のコストを以下にまとめる。

割り算
割り算($R_a[X] \div R_b[Y]$)に対するアルゴリズムを考える。
直接法
ソートを利用する場合
$R_a$の$X$をマイナー、$X_c$をメジャーでソートし、$R_b$も$X$でソートする。このとき、$X_c$が変わる毎に$X$を付き合わせて最後まで一致すれば商に追加。

ハッシュを利用した場合
$R_b$に対応したハッシュテーブル$H_1$と商の候補のハッシュテーブル$H_2$に$R_b$に対応したbitを用意する。すなわち、$R_a$をハッシュし$H_1$のエントリを調べ、$H_2$のbitを立てる。

間接法
集約演算を用いる。すなわち、$R_a$をGroup-Byし、$R_b$と同じCountか調べる。あらかじめR_aをR_bでSemi-Joinしておくことが必要。

準結合(Semi-Join)
準結合とは、リレーションRとSの自然結合結果から、Sにのみ存在する属性を射影演算にて除去する演算である。
<参考>
https://www.slideshare.net/shoheiyokoyamaac/04-27443570
等結合の結果が一方の関係のみ。このとき基本的なコストは等結合と同じであり、集合演算や、分散データベース等で転送データを絞り込む時に用いられる。
集合積
全ての属性に対する等結合または準結合
集合和
2つの関係の結合後の重複除去。または、一方の関係と集合差との結合で表される。
集合差
全ての属性に対して準結合の結果の補集合タプルを選択(Anti-Semi-Join)。コストは等結合と同じ。