関係演算アルゴリズムとコスト
この記事は大学の期末試験勉強のために作成したものです。間違い等は悪しからず。
関係データベース演算の種類
- 入力演算
- 選択(Selection)
- 射影([Delta] Projection)
- 集約(Aggregation)
- 整列(Order-By)
- 重複除去(Duplication Elimination)
- グループ化(Group-By)
- 結合(Join)
- 準結合(Semi-Join)
- 集合積(Intersection)
- 集合差(Difference)
- 集合和(Union)
- 直積(Cartesian Product)
- 商(Division)
演算のコスト見積もり
比較回数(CPUコスト)とディスクI/Oによって見積もる。また以下の議論では、関係代数Rのサイズを以下で定義する。
- Rのタプル数:$\{R\}$
- Rのディスクページ数:$|R|$
各選択演算とコストの見積もり
選択演算(Selection)のコスト
SELECT * FROM ~ ;
データベースにIndexがない場合
- 比較回数:$\{R\}$(Rのタプル数に等しい)
- ディスクI/O回数:$|R|$(Rのディスクページ分だけI/O)
データベースにIndexがある場合
- B木ベースのIndexの場合
- 比較回数、I/O回数共に、$\log_F\{R\}+1$
- ハッシュIndexの場合
- 比較回数、I/O回数共に、定数回($O(1)$)
射影演算(Projection)のコスト
SELECT [DISTINCT] query1, query2 FROM ~ ;
今、重複除去(Delta)を行わないとする。
Indexの効果は無いので、全スキャンを行う。すなわち
- タプルアクセス:$\{R\}$(Rのタプル数に等しい)
- ディスクI/O回数:$|R|$(Rのディスクページ分だけI/O)
集約演算(Aggregation)
SELECT COUNT( * ) FROM ~ ;
他にもSUM()やAVE()など。
Indexの効果は無いので、全スキャンを行う。すなわち
- 比較回数:$\{R\}$(Rのタプル数に等しい)
- ディスクI/O回数:$|R|$(Rのディスクページ分だけI/O)
整列演算(Order-By)
データがCPUメモリ上に乗る場合は、一般のソートアルゴリズムを用いる。

<参考>
https://postd.cc/how-does-a-rdb-work-1/#Merge_Sort
データがCPUメモリ上に乗らない場合は、外部ソートを用いる。このとき、ディスクアクセスを前提とするとクイックソートは適さない。なぜならば、最初に論理キーで分割するため、サイズが一定でないからである。そこでマージソート、特に2-wayマージソートを用いる。(2-wayマージした各段をディスクに格納)
重複除去(Duplication Elimination)のコスト
ソートを利用した場合
-
比較の回数:$\{R\}(\log \{R\} + 1)$
- ソート(マージソート)をする:$\{R\} \log \{R\}$
- (成立したデータに対し)比較:$\{R\}$
-
ディスクI/O:$|R|(2\log |R| + 1)$
- 各段での読み出し:$2|R| \log |R|$
- 結果の格納:$|R|$
ハッシュを利用した場合
同じハッシュバケット(ハッシュテーブルにおける各スロットのこと。衝突が起きやすいハッシュテーブルでは各スロットが単一レコードでなくレコードの集合に対応していることが多いためこう呼ばれる)の中で同じ値を除去すればよい。
- 比較回数:$\{R\}$
- ディスクI/O:$|R|$
グループ化演算(Group-by)のコスト
SELECT query1, Sum(query2)
FROM "foo"
GROUP BY "bar
入れ子ループ(ネステッド・ループ)を用いる場合
query1を固定してグループに対応する全てのものを探索するので、組み合わせ演算と等価。( $ {}_R \mathrm{C} _2$ )
-
比較回数:$ \frac{ \{R\} (\{R\} - 1)}{2} $
- ( $ {}_R \mathrm{C} _2$ )
-
ディスクI/O:$\frac {|R|(|R|+1) }{2} $
- 最後にディスクに結果を書き込む。
ソートを用いる場合
重複除去のソートの場合と同じ。
-
比較の回数:$\{R\}(\log \{R\} + 1)$
- ソート(マージソート)をする:$\{R\} \log \{R\}$
- (成立したデータに対し)比較:$\{R\}$
-
ディスクI/O:$|R|(2\log |R| + 1)$
- 各段での読み出し:$2|R| \log |R|$
- 結果の格納:$|R|$
ハッシュを用いる場合
- 比較回数:$\{R\}$
- ディスクI/O:$|R|$
結合演算(Join)のコスト
SELECT *
FROM DB1, DB2
WHERE DB1.hoge = DB2.huga;
入れ子ループの場合
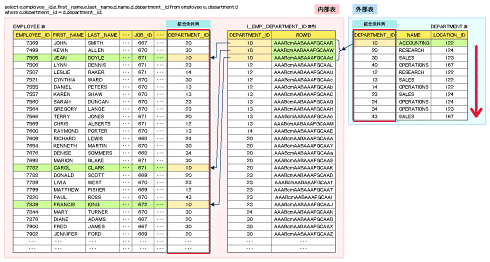
- 比較回数:$\{R\} \times \{S\}$
- ディスクI/O:$|R| \times |S|$
ソートマージ結合を用いる場合
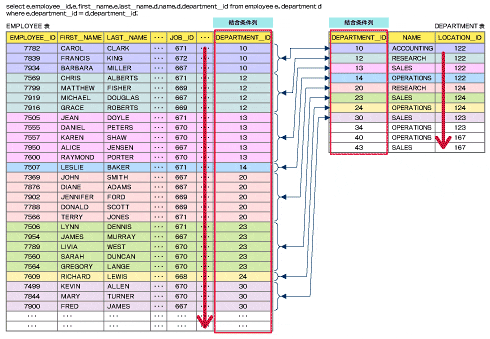
2つのデータベースをそれぞれソートし、この2つをマージする。
-
比較回数:$\{R\}(\log \{R\} + 1) \times \{S\}(\log \{S\} + 1)$
-
ディスクI/O:$|R|(2\log |R| + 1) + |S|(2\log |S| + 1)$
ハッシュ結合を用いる場合
等結合(=)のみ可能で、両方の関係のタプルに同じハッシュ関数を適用することで実現。
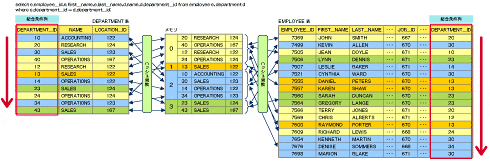
RとSの全タプルが計算メモリに乗る場合...
- レコード数の少ない表(図3ではDEPARTMENT表)の結合条件列(DEPARTMENT_ID列)をハッシュ関数にかけ、メモリ上にハッシュ・テーブルを作成する。 -> BUILD
- もう一方の表(図3ではEMPLOYEE表)の結合条件列(DEPARTMENT_ID列)をハッシュ関数にかけ、結合できるかをハッシュ・テーブルで確認する。 -> PROBE
- ハッシュ値が等しいレコードを結合して結果を返す。
ハッシュテーブルのバケット数を$n$として、
- ハッシュ関数の適用の回数:$\{R\} + \{S\}$
- 比較の回数:$\{R\}/n \times \{S\}/n \times n$
RとSの全タプルが計算メモリに乗らない場合...
- 単純ハッシュ結合
- GRACEハッシュ結合
- ハイブリッド結合
ハッシュテーブルに使えるメモリ量を$|M|$、タプルサイズについて$|R| > |S|$、また属性値は均等に分散していると仮定する。
単純ハッシュ結合とそのコスト
ハッシュテーブルに入りきらない部分をディスクに格納し、これをオーバーフロー分がなくなるまで繰り返す。この時の繰り返しの回数$L$は平均で$L = |R|/|M|$
比較回数
この時の計算コストは、ハッシュ適用回数と比較回数にて決まる。
ハッシュ適用1回目
- ハッシュ適用回数:$\{R\} + \{S\}$
- 比較回数:$\{S\}/L$
ハッシュ適用i回目
- ハッシュ適用回数:$\{R\} - (i-1)\times \{R\}/L + \{S\} - (i-1)\times \{S\}/L$
- 比較回数:$\{S\}/L$
全体として
上式の$i = 1, ... , L$の和を取ればよいので、
- ハッシュ適用回数:$(|R|+|M|) \times (\{R\} + \{S\}) / (2|M|) $
- 比較回数:$\{S\}$
ディスクI/O
1回目
- 読み出し:$(|R|+|S|)$回
- 書き込み:$(|R|-|M| + |S| - |S|/L)回
2回目以降i回目
- 読み出し:$((|R|+|S|) - (i-1) \times (|R|+|S|)/L$回
- 書き込み:$((|R|+|S|) - i \times (|R| + |S|)/L$回
全体として
上式の$i = 1, ... , L$の和を取ればよいので、$|R|(|R|+|S|)/|M|$
参考
https://postd.cc/how-does-a-rdb-work-1/#Merge_Sort
https://www.atmarkit.co.jp/ait/articles/0408/25/news101.html