はじめに
千葉大学大/Nospareの米倉です.今まで赤池情報量規準(AIC),ベイジアン情報量規準(BIC)等について解説してきました.そこで今回はそもそも情報量規準とは何かについて4つの分類に基づき解説していきたいと思います.
モデル選択
情報量規準とは一言でいうとモデルを選択する際に使われる,モデルの良し悪しの指標のことです.統計的分析をする際,何かしらの統計モデルを構築してパラメータを推定し,予測なり仮説検定なりを行います.この時,複数の候補となるモデルの中からどのモデルを使うべきかを知る必要があるのですが,情報量規準はどのようなモデルを選ぶべきかを我々に教えてくれます.基本的には情報量規準を計算して,その値が最小のものを「良い」統計モデルとして採用します.
KLタイプorエビデンスタイプ
情報量規準はモデルの良し悪しを測る尺度と言うことを述べましたが,ではどうやってそれを測るのでしょうか.これは大きく分けて,カルバックライブラー情報量を用いる方法とエビデンス(周辺尤度)を用いる方法の2つにまず分類できます.
今,$p_\star(y_{0:n})$を「真」の分布とし,$\hat p_\theta(y_{0:n})$を分析者が用いる予測モデルの尤度としましょう.ここでいう予測モデルとは統計モデルのパラメータを何らかの方法で推定し,それを統計モデルに挿入したものを指します.この時,それらのカルバックライブラー情報量は$$KL:=\int p_\star(y_{0:n})\log p_\star(y_{0:n})dy_{0:n}-\int p_\star(y_{0:n})\log \hat p_\theta(y_{0:n})dy_{0:n}$$と定義されます.$KL=0$のとき$p_\star(y_{0:n})=\hat p_\theta(y_{0:n})$が成立するので,この値が小さいほど良いモデルだと言えそうです.ここで第一項は統計モデルに依存しない項(分析者が出来ることは何もない)なので無視をし,第二項$R(\theta):=\int p_\star(y_{0:n})\log \hat p_\theta(y_{0:n})dy_{0:n}$のみに着目します.そうすると,カルバックライブラー情報量を最小化することと,第二項を最大化することが等しくなることが分かります.よって,この第二項を上手く推定できればその大小を比較してモデル選択に利用できます.このようにカルバックライブラー情報量に基づいて構成される情報量規準を,KLタイプと呼ぶことにします.具体的には後程紹介するAIC,DIC,WAICがKLタイプです.
一方,統計学では「エビデンス」ともよばれる周辺尤度を最大化するモデルを選ぶことも推奨されています.パラメタ$\theta$に対して事前分布$p(\theta)$と尤度関数$p_{\theta}(y_{0:n})$を分析者が設定します.この時$$m(y_{0:n})=\int p_{\theta}(y_{0:n})p(\theta)d\theta$$のことをエビデンス(周辺尤度)と呼びます.エビデンスを用いる実用上の問題として.パラメータに対しての積分をする必要があるので,解析的な表現を得られないことが多々あります.BICやWIBCはエビデンスの近似・推定量となっており,最大の値を持つモデルを選ぶことが推奨されます.実用上は,KLタイプと整合的にするために,マイナスをかけたものを情報量規準として採用するので,最小の値を持つモデルを選ぶことがになります.エビデンスの推定を目的とする情報量規準をエビデンスタイプと呼ぶことにします.
この様に推定しようとしているものがカルバックライブラー情報量かエビデンスかで,情報量規準は先ず分類ができます.
頻度論orベイズ
次の分類の仕方は,予測モデル$\hat p_\theta(y_{0:n})$の構成方法です.頻度論的発想では,最もポピュラーの方法は統計モデルのパラメータ$\theta$は最尤推定し,その最尤推定値$\hat\theta$を$ p_\theta(y_{0:n})$に代入した$p_\hat\theta(y_{0:n})$を予測モデルとして用いる方法です.このタイプの予測モデルを用いた情報量規準を頻度論タイプと呼ぶことにします.AICとBICが頻度論タイプにあたります.
一方,ベイズ推定では事後分布$\Pi(\theta\mid y_{0:n})$に基づき推論を行います.例えば事後平均$\int\theta\Pi(\theta\mid y_{0:n})d\theta$を用いてパラメタを推定したり,この様に何か事後平均を用いて予測モデルを構築した時の情報量規準をベイズタイプと呼ぶことにします.DIC, WAIC, WBICがベイズタイプに分類できます.
この様に,情報量規準は用いる予測モデルが頻度論的かベイズ的かでも分類が出来ます.
AIC
AICは$\theta$の推定量として,最尤推定量を用いてそれを基に予測モデル$p_{\hat\theta}(y_{0:n})$を構築します.またこのままだと$R(\theta)$の推定量として,バイアスをもってしまいます.$$AIC:=-2\log p_{\hat \theta}(y_{0:n})+2d$$と定めると,$n$を大きくしたときに$R(\theta)$のバイアスが無い推定量になることが示せます.ここで$d$はパラメータの数です.これを赤池情報量規準(AIC)といいます.なのでAICはKL-頻度論タイプの情報量規準です.
BIC
BICは予測モデルとして,AICと同様に$p_{\hat\theta}(y_{0:n})$を用います.なのでベイズ的な情報量規準ではないです.これをエビデンスの定義式に代入して,ラプラス近似を最尤推定値周りで行うと,エビデンスの推定量として$$BIC:=-2\log p_{\hat \theta}(y_{0:n})+d\log n$$を得ることが出来ます.これをベイジアン情報量規準(BIC)と呼びます.BICはエビデンス-頻度論タイプの情報量規準です.
DIC
DICは予測モデルとして対数尤度の事後平均$\int \log p_\theta(y_{0:n})\Pi(\theta\mid y_{0:n})d\theta$を採用します.この時DICは$E_{\Pi}[R(\theta)]$の最大化を行い,AICの時と同様にバイアスの除去したものとして,$$DIC:=-2\int \log p_{\theta}(y_{0:n})\Pi(\theta|y_{0:n})d\theta+p_{DIC}$$がを推定量として採用します.$p_{DIC}$はバイアス補正項で,詳しくはこの記事を参照して下さい.以上より,DICはKL-ベイズタイプの情報量規準です.
WAIC
WAICでは予測モデルとして,$\sum_i^{n}\log \int p(y_{i}|\theta)\Pi(\theta|y_{i})d\theta$を採用します.この時AICと同じように$R(\theta)$の推定を目指すのですが,AICが$R(\theta)$のよい推定量になるためにはいくつかの条件があります.典型的なのが,予測モデルが正規分布を用いてある意味で近似できるための条件です.いくつかの統計モデルではこの条件を満たさないため,AICは$R(\theta)$の良い推定量にはなりません.しかし$$WAIC:=-\sum_i^{n}\log \int p(y_{i}|\theta)\Pi(\theta|y_{i})d\theta+2\sum_{i}^{n}Var_{\Pi(\theta|y_{i})}[\log p(y_{i}|\theta)]$$はその様な条件でも$R(\theta)$の良い推定量となることが示せ,これを広く使える情報量規準(WAIC)と呼びます.ここで$Var_{\Pi(\theta|y_{i})}[A]$はAの事後分散です.以上より,WAICはKL-ベイズタイプの情報量規準とできるので,WAICとDICは同じ分類となります.
WBIC
BICはエビデンスのラプラス近似として求められますが,WAICの時と同様にそれが可能になるためには,例えば統計モデルが正規分布で近似出来る必要があり,考えているモデル次第ではそれが出来ないことがあります.WBICではまず逆温度と呼ばれる数列$1=\phi_0>\phi_1,...,>\phi_n$を用いて,それでパラメタライズされた事後分布$\Pi(\theta|y_{0:n})^{\phi_n}$を考えます.この時$\log m(y_{0:n})=\frac{\int \log p_{\theta}(y_{0:n})p_{\theta}(y_{0:n})^{\phi_n^\star}p(\theta)d\theta}{\int p_{\theta}(y_{0:n})^{\phi_n^\star}p(\theta)d\theta}$となる最適な逆温度の列$\phi_n^\star$が,ラプラス近似が用いられない条件でも存在することを示すことが出来ます.具体的には$\phi_n=1/\log n$とすると,$n$を十分に大きくすると$\phi_n^\star$と同等になることが示せます.そこで広く使えるベイジアン情報量規準(WBIC)は$$WBIC:=\frac{\int \log p_{\theta}(y_{0:n})p_{\theta}(y_{0:n})^{1/\log n}p(\theta)d\theta}{\int p_{\theta}(y_{0:n})^{1/\log n}p(\theta)d\theta}$$と定義され,これはラプラス近似が用いられない時にでもエビデンスの良い推定量となります.弱点としてはBICと違い積分項が存在するため,数値的に求めるのが実用上大変なことが多いところです.以上より,WBICはエビデンス-ベイズタイプの情報量規準です.
分類のまとめ
どの予測モデルで何を推定しようとするのかで,情報量規準は計4通りの分類が出来ることを見てきました.以下は4分類のまとめの図です.
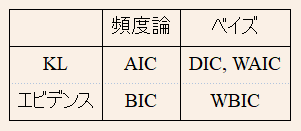
KLタイプとエビデンスタイプの特徴
一般的に,KLタイプの情報量でモデルを選択すると,minimax最適性という予測誤差の最悪の値を最小化する性質があります.つまり予測の意味で,最悪のケースを防ぐことが出来るのである意味で保守的なモデル選択が可能です.,例えばAICでは様々なモデルでこの性質を持っていることが示されています.一方でエビデンスタイプの情報量規準でモデルを選択すると考えている統計モデルに「真の」モデルが含まれている時に,真のモデルを確率1で選択できる性質があります.また含まれていない時でも,ある意味で正しいモデルを選択することができます.例えばBICでは様々なモデルでこの性質を持っていることが示されています.興味深いことに一般的にこの二つの性質を同時にもつ情報量規準を構築することは出来ず,トレードオフの関係にあります.
この様に情報量規準は推定するターゲットと推定方法で区別することが出来て,またその性質は推定ターゲットにより決定されます.
おわりに
今回の内容に関連する共同研究・各種お問い合わせにつきましては,お気軽に米倉までご連絡ください.また,株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospare までお問い合わせください.
