こんにちは、(株)日立製作所 Lumada Data Science Lab. の中川です。普段は人工知能を制御に適用する研究に従事しています。近年、機械学習が注目される中、機械学習理論および機械学習を使った技術開発環境は急速に進歩すると共に、多くの方がデータサイエンスに関わるようになってきました。すでにデータサイエンスに携わっている方や、これからデータサイエンスに関わってみようと思っている方の中で、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから基本的な内容で記事を書きます。今回は、「線形単回帰における区間推定・検定と線形重回帰における区間推定・検定の差違」および「正規分布、線形単回帰、線形重回帰の関係の俯瞰」についてご紹介します。
1. はじめに
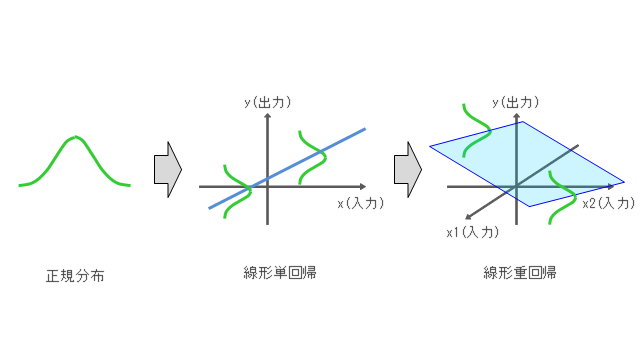
”正規分布”と”線形回帰”という言葉を聞いたとき、両者の関連性が思い浮かぶでしょうか。また、”線形単回帰”と”線形重回帰”の相違点について、はいかがでしょうか。統計学においては、データ(標本)を用いて線形回帰(単回帰、重回帰に関わらず)を求めるとき、一般にデータの分布は正規分布であることを仮定しています。データから求めた線形回帰の信頼性・妥当性を評価するとき、正規分布における区間推定・検定の考え方を適用します。「線形単回帰における区間推定・検定」と「線形重回帰における区間推定・検定」を比べることで、両者の差を説明したいと思います。
2.「線形単回帰における区間推定・検定」
2-1. 線形単回帰の信頼区間の区間推定
(1)式は、線形単回帰における母回帰($y_k$の真値)の信頼区間の区間推定を示す式です。
$$
\begin{align}
&\hat{y}_k-(t(\phi,\alpha){\cdot}s{\cdot}\sqrt{h_{{kk}}}){;}{\leqq}{;}y_{k}{;}{\leqq}{;}\hat{y}_k-(t(\phi,\alpha){\cdot}s{\cdot}\sqrt{h_{{kk}}}){\quad}・・・・(1)\
&{\quad}\hat{y}_k=\hat{a}・x_k+\hat{b}\
&{\quad}x_k:信頼区間を評価したいy_kに対応するxの値\
&{\quad}t(\phi,\alpha):自由度\phi, 信頼区間を指す値\alphaから決まるt分布の値\
&{\quad}1-\alpha:信頼係数\
&{\quad}s^2:分散\
&{\quad}h_{kk}=1/n+{(x_k-\bar{x})^2/\Sigma_{i=1}^{n}(x_i-\bar{x})(x_i-\bar{x})}:てこ比\
\end{align}
$$
(1)式で表される線形単回帰の区間推定の式は、正規分布の区間推定を線形単回帰に拡張したもので、(1)式で示される区間に$y$(ノイズを除去した後の真の$y$の値)が100・(1-$\alpha$)%の確率で収まることを指します。このように、(1)式を使えば、100・(1-$\alpha$)%の信頼区間を定量的に求めることができ、線形単回帰の信頼度を定量的に表すことができます。
2-2. 線形単回帰の回帰係数の検定
線形単回帰の検定で一般的なのは、回帰係数$a$の値が0であるか否か検定することです。$a$=0のとき、$y$は$x$に対して相関を持たないことになり、線形単回帰を用いることの妥当性がなくなります。(2)式は、線形単回帰における回帰係数$a$の検定の考え方を示した式です。(2)式において、$a$=0として検定を行います。
$$
\begin{align}
&{\quad}a-(t(\phi,\alpha){\cdot}s{\cdot}\sqrt{\frac{1}{S_{xx}}}{;}){;}\leqq{;}\hat{a}{;}\leqq{;}a+(t(\phi,\alpha){\cdot}s{\cdot}\sqrt{\frac{1}{S_{xx}}}{;}){\quad}・・・(2)\
\mspace{1cm}\
&{\quad}S_{xx}=\sum_{i=1}^{n}(x_i-\bar{x})(x_i-\bar{x})\
\end{align}
$$
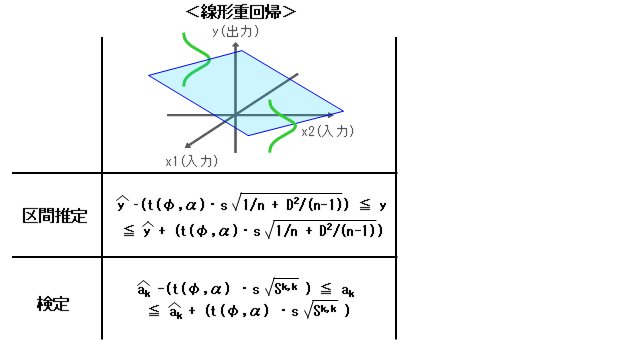
3.「線形重回帰における区間推定・検定」
3-1. 線形重回帰の信頼区間の区間推定
(3)式は、線形重回帰における母回帰($y_k$の真値)の信頼区間の区間推定を示す式です。
$$
\begin{align}
&\hat{y}_k-(t(\phi,\alpha){\cdot}s{\cdot}\sqrt{H_{kk}{;}}){;}{\leqq}{;}y_{k}{;}{\leqq}{;}\hat{y}_k+(t(\phi,\alpha){\cdot}s{\cdot}\sqrt{H_{kk}}{;}){\quad}・・・・(3)\
&{\quad}\hat{y}_k=\hat{a}_1・x_{1,k}+\hat{a}_2・x_{2,k}+・・・+\hat{a}_m・x_{m,k}+\hat{b}\
&{\quad}x_{i,k}:信頼区間を評価したいy_kに対応するxの値\
&{\quad}{\quad}{\quad}i=1,2,・・・,m\
&{\quad}{\quad}{\quad}k=1,2,・・・,n\
&{\quad}t(\phi,\alpha):自由度\phi,信頼区間を指す値\alphaから決まるt分布の値\
&{\quad}1-\alpha:信頼係数\
&{\quad}s^2:分散\
&{\quad}H_{kk}=\frac{1}{n}+\frac{D^{2}_k}{(n-1)}\
&{\quad}D^{2}_k=(n-1)\sum_{i=1}^{m}\sum_{j=1}^{m}(x_{i,k}-\bar{x}_i)(x_{j,k}-\bar{x}_j)S^{i,j}:マハラノビス距離の2乗\
&{\quad}S^{i,j};xの分散共分散行列の逆行列の(i,j)成分\
\end{align}
$$
(3)式で表される線形重回帰の区間推定の式は、(1)式で示しました線形単回帰の区間推定を拡張したものです。(3)式を使えば、100・(1-$\alpha$)%の信頼区間を定量的に求めることができ、線形重回帰の信頼度を定量的に表すことができます。(1)式と(3)式を比較しますと、(1)式における$h_{kk}$が、(3)式では、$H_{kk}$となっています。において$m$=1のとき、$H_{kk}$=$h_{kk}$となり、両者は等価です。なお、(3)式においては、自由度$φ$=$n$ - $m$となります。
3-2. 線形重回帰の回帰係数の検定
線形重回帰の検定で一般的なのは、線形単回帰と同じく、回帰係数$a_i$の値が0であるか否か検定することです。$a_i$=0のとき、$y$は$x$に対して相関を持たないことになり、線形単回帰を用いることの妥当性がなくなります。(4)式は、線形単回帰における回帰係数$a_i$の検定の考え方を示した式です。(4)式において、$a_i$=0として検定を行います。
$$
\begin{align}
&a_i-(t(\phi,\alpha){\cdot}s{\cdot}\sqrt{S^{i,i}}\hspace{0.12cm}){;}\leqq{;}\hat{a}_i{;}\leqq{;}a_i+(t(\phi,\alpha){\cdot}s{\cdot}\sqrt{S^{i,i}}\hspace{0.12cm}){\quad}・・・(4)\
\mspace{1cm}\
&i=1,2,・・・,m\
\end{align}
$$
(2)式と(4)式を比較しますと、(2)式における$1/S_{xx}$は、(4)式では$S^{i,i}$となっています。$S^{i,i}$において$m$=1のとき、$S^{i,i}$ = $1/S_{xx}$となり、両者は等価です。
3-3. 線形重回帰における予測区間の区間推定
参考までに、線形重回帰における予測区間の区間推定についても、紹介しておきます。(5)式と(6)式は、それぞれ線形単回帰の予測区間の区間推定の式と線形重回帰の予測区間の区間推定の式です。
$$
\begin{align}
&\hat{y}_k-(t(\phi,\alpha){\cdot}s{\cdot}\sqrt{h_{kk}+1}{;}){;}{\leqq}{;}y_{k}{;}{\leqq}{;}\hat{y}_k+(t(\phi,\alpha){\cdot}s{\cdot}\sqrt{h_{kk}+1}{;}){\quad}・・・・(5)\
\mspace{1cm}\
&\hat{y}_k-(t(\phi,\alpha){\cdot}s{\cdot}\sqrt{H_{kk}+1}{;}){;}{\leqq}{;}y_{k}{;}{\leqq}{;}\hat{y}_k+(t(\phi,\alpha){\cdot}s{\cdot}\sqrt{H_{kk}+1}{;}){\quad}・・・・(6)\
\end{align}
$$
(5)式と(6)式を比較しますと、(5)式における$h_{kk}$が、(6)式では、$H_{kk}$となっています。$H_{kk}$において$m$=1のとき、$H_{kk}$=$h_{kk}$となり、両者は等価です。また、(4)式と(6)式を比較すると、(6)式では、$\sqrt{H_{kk}}$の部分が、$\sqrt{H_{kk}+1}$となっており、観測時のノイズが考慮されていることがわかります。
4.「正規分布、線形単回帰、線形重回帰の関係の俯瞰」
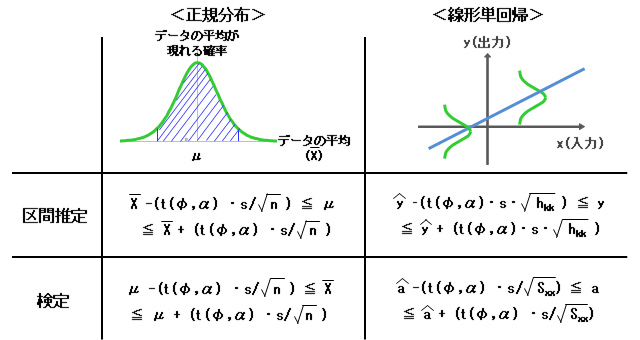
下表に、正規分布、線形単回帰および線形重回帰それぞれにおける区間推定と検定の式を示します。3者の相違点および関係性がご理解頂けるのではないかと思います。
5. おわりに
今回は、「線形単回帰における区間推定・検定と線形重回帰における区間推定・検定の差違」および「正規分布、線形単回帰、線形重回帰の関係の俯瞰」についてご紹介しました。正規分布における区間推定・検定の考え方が線形単回帰および線形重回帰の区間推定・検定に拡張適用されていることがおわかり頂けたとしたら幸いです。正規分布を仮定している理論・方法は、いろいろあります。また、世の中の正規分布になっている現象もあります。正規分布を仮定している理論・方法、正規分布となっている現象を探してみるのも、さらに知見が広がって、おもしろいかもしれません。
今回も、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから記事を書かせて頂きました。より詳しく知りたいという方は、参考文献などをご参考頂ければと思います。
参考文献
東京大学教養学部学部統計学教室編:統計学入門
永田靖:入門統計解析法
永田靖,棟近雅彦:多変量解析法入門