こんにちは、(株)日立製作所 Lumada Data Science Lab. の中川です。普段は人工知能を制御に適用する研究に従事しています。近年、機械学習が注目される中、機械学習理論および機械学習を使った技術開発環境は急速に進歩すると共に、多くの方がデータサイエンスに関わるようになってきました。すでにデータサイエンスに携わっている方や、これからデータサイエンスに関わってみようと思っている方の中で、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから基本的な内容で記事を書きます。今回は、ロジスティック回帰の検定をご紹介すると共に、線形重回帰の検定と比較することで、両者の比較を行います。
1. はじめに
ロジスティック回帰は、目的変数を確率で扱う場合に適用する線形モデルです。線形回帰は目的変数は、-$\infty$から$+\infty$までの値を取りえますが、ロジスティック回帰では、目的変数は0~1の値となります。以下の内容で御説明致します。
・ロジスティック回帰のおさらい
・正規分布と$\chi^2$分布を用いた検定
・ロジスティック回帰における代表的な検定
・線形重回帰における検定との比較
2. ロジスティック回帰のおさらい
(1)式は、ロジスティック回帰の式を示しています。
$$
\hat{y}=\frac{1}{1+exp(-(\hat{a}_1x_1+\hat{a}_2x_2+\cdots+\hat{a}_nx_n+\hat{b}))}\hspace{0.5cm}・・・(1)\
$$
もともとロジスティック回帰は、ある疾患の発生確率$p(=y)$を求めるための式から得られました。(1)式における各項の意味は下記です。
$y$:ある事象(疾患)の発生確率
$\hat{b}$:ベースオッズの対数
$\hat{a}_k$:オッズ比の対数
$x_k$:ある事象(疾患)を発生させる(リスク)要因の有無、カテゴリーなど
オッズ:ある事象の起こりやすさを示す。
(ある事象が起こる確率(回数))/(ある事象が起こらない確率(回数))
オッズ比:ある条件1でのオッズに対する異なる条件2でのオッズの比
$\hat{b}$と$\hat{a}_k$の値を最尤推定法を用いて決定します。統計学においては、標本データあるいは標本データを統計処理した結果の有意性を検証するための方法として検定というものがあります。ロジスティック回帰においても、データから値を決定した対数オッズ比($\hat{a}_k$)の有意性を検証する検定があります。以下、ご紹介します。
3. 正規分布とカイ二乗分布を用いた検定
3-1. 正規分布を用いた検定
まず、正規分布を用いた検定をおさらいします。(2)式は、正規分布における標本データの平均$\bar{X}$の検定の考え方を示した式です。
$$
\begin{array}
-&-1.96 \leqq \frac{\bar{X}-\mu}{\sigma} \leqq 1.96\hspace{0.4cm}・・・(2)\
&\mspace{1cm}\
&\hspace{1cm}\bar{X}:標本平均(データから求める平均)\hspace{2.5cm}\
&\hspace{1cm}\sigma^2:分散(データから求める分散)\
&\hspace{1cm}\mu:母平均(真の平均)\
\end{array}
$$
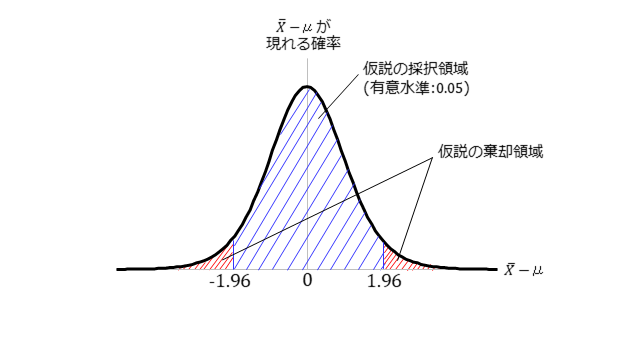
母平均$μ$に仮定した値(例えば0)を入れて、標本データから得た標本平均$\bar{X}$が(2)式に当てはまるか否かを確かめます。当てはまれば、仮定した母平均$\mu$の値に妥当性があるとして採択します。当てはまなければ、仮定した母平均$\mu$の値に妥当性がないとして棄却します。(2)式中の1.96は、採択範囲(棄却範囲)を規定している値で事前に決めます。1.96は、95%の範囲を採択範囲(5%を棄却範囲)とするという意味で、採択範囲に応じて値を変えます。採択する仮説を帰無仮説と呼び、棄却する仮説を対立仮説と呼びます。本例では、「母平均$\mu=0$である」が帰無仮説であり、「母平均$\mu{\neq}0$である」が対立仮説です。
(2)式は、真の値(真の平均$\mu$)と真の分散($\sigma^2$)からなっており、いわば、中央値と許容範囲から成り立っている式であることがわかります。正規分布における検定とは、仮定する真の値を中央値とし、仮定した真の値に対して実際に観測される値がばらつく許容範囲を分散の近似値で決めていると言えます。下図は、正規分布における検定の考え方を簡単に示しています。
本例では、標本平均を対象とした検定を示しましたが、正規分布する統計量であれば、正規分布を用いた検定を適用できます。
3-2. カイ二乗分布とカイ二乗分布を用いた検定
3-2-1. カイ二乗分布
次に、$\chi^2$(カイ二乗)分布をおさらいします。$\chi^2$分布は、下記のように定義されます。
$$
\begin{array}
,&\chi^2は、自由度nの\chi^2分布である。\
,&\chi^2={z_1}^2+{z_2}^2+\cdots+{z_n}^2\hspace{0.4cm}・・・(3)\
,&ここに、z_k(k=1,2,・・・,n)は、それぞれ独立な標準正規分布の確率変数である。\
\end{array}
$$
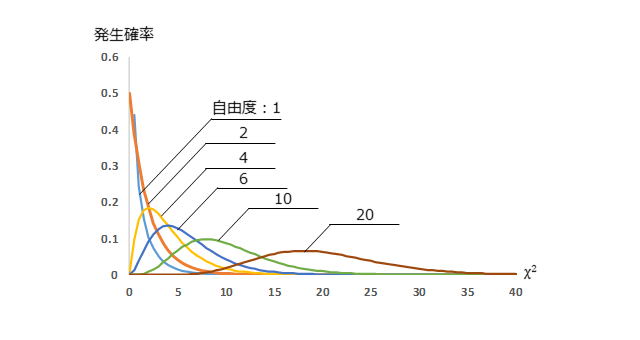
下図は、$\chi^2$分布の例を示しています。自由度に応じて、分布が変わります。
$k=1$のとき、${z_1}^2$は標準正規分布の確率変数の2乗と等価で、いわば標準正規分布と自由度1の$\chi^2$分布は表裏一体と言えます。
3-2-2. カイ二乗分布を用いた検定
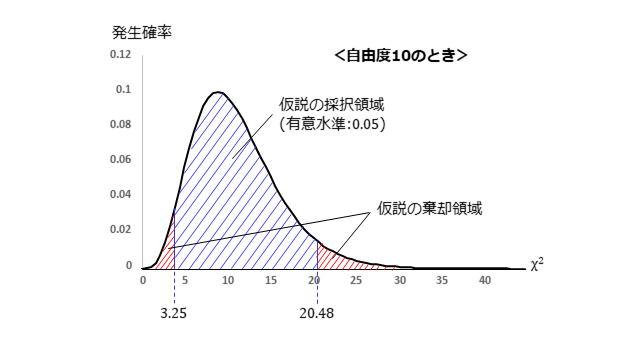
$\chi^2$分布を用いた検定をおさらいします。下図は、自由度10のときの$\chi^2$分布における検定の考え方を簡単に示しています。正規分布における検定と考え方は同じですが、$\chi^2$分布は正値しかとりません。正規分布における検定と同じく、$\chi^2$分布する統計量であれば、$\chi^2$分布を用いた検定を適用できます。
4. ロジスティック回帰における代表的な検定
4-1. ロジスティック回帰における検定の考え方
前章で、正規分布する統計量であれば正規分布を用いた検定を適用でき、$\chi^2$分布する統計量であれば$\chi^2$分布を用いた検定を適用できることをおさらいしました。ロジスティック回帰における検定は、オッズ比の対数($\hat{a}_k$)を対象に行います。$k$番目の対数オッズ比($\hat{a}_k$)に意味があるか、すなわち、$k$番目の対数オッズ比($\hat{a}_k$)は、ある事象の発生確率を予測するロジスティック回帰式において、必要なパラメータであるかを確かめます。具体的には、$k$番目の対数オッズ比($\hat{a}_k$)を0($\hat{a}_k$は必要ない)という仮説を立てて、標本データから得られた$\hat{a}_k$の値あるいは$\hat{a}_k$を基にした統計量が前章でご紹介した正規分布もしくは$\chi^2$分布の仮説の採択領域にあるか否かを確かめます。これは、線形回帰の回帰係数の検定と同じ考え方です。ロジスティック回帰の代表的な検定方法として、Wald検定、尤度比検定、スコア検定の3つがあります。以下、3つの検定方法を簡単にご紹介します。
4-2. Wald検定
Wald検定は、Wald統計量を用いて正規分布もしくは$\chi^2$分布で検定を行います。Wald統計量は(4)式で表され、漸近的に標準正規分布することが知られています。
$$
\begin{array}
,&\frac{\hat{a}_k}{SE}\hspace{0.4cm}・・・(4)\hspace{2.5cm}\
\mspace{1cm}\
,&SE:標準誤差\
\end{array}
$$
(4)式から、$a_k=0$を仮説としたときの正規分布における検定(有意水準0.05)を表す式は(5)式となります。
$$
-1.96\leqq\frac{\hat{a}_k}{SE}\leqq1.96\hspace{0.4cm}・・・(5)\
$$
$\hat{a}_k$が(5)式を満たすとき、仮説は妥当性があるとして採択します。
前章で紹介しましたように、標準正規分布の2乗は、自由度1の$\chi^2$分布と一致しますので、$a_k=0$を仮説としたときの$\chi^2$分布における検定(有意水準0.05)を表す式は(6)式となります。$\hat{a}_k$が(6)式を満たすとき、仮説は妥当性があるとして採択します。
$$
\Bigl(\frac{\hat{a}_k}{SE}\Bigl)^2;\leqq3.84\hspace{0.4cm}・・・(6)\
$$
(5)式と(6)式は、いずれも、対数オッズ比($\hat{a}_k$)を一つずつ検定するものです。一方で、(3)式より複数の対数オッズ比($\hat{a}_k$)を同時に検定できることがわかります。複数(r個)の対数オッズ比($\hat{a}_{n-r+1},\hat{a}_{n-r+2},$$\cdots,\hat{a}_n$)を同時に検定する式(有意水準0.05)は(7)式となります。
$$
\begin{array}
,&\chi^2_L(\phi,0.05)\leqq\theta^T{V^{-1}}\theta\leqq\chi^2_H(\phi,0.05)\hspace{0.4cm}・・・(7)\
&\mspace{1cm}\
&\hspace{1cm}\theta=[,\hat{a}_1, \hat{a}_2,\cdots,\hat{a}_{n-r+1}(=0),\hat{a}_{n-r+2}(=0),\cdots,\hat{a}_n(=0),]\
&\hspace{1cm}V:\hat{a}_kの分散共分散行列\
&\hspace{1cm}\chi^2_L(\phi,0.05):自由度\phi、有意水準0.05のときの\chi^2分布の下側値\
&\hspace{1cm}\chi^2_H(\phi,0.05):自由度\phi、有意水準0.05のときの\chi^2分布の上側値\
&\hspace{1cm}\phi:自由度(=r)\
\end{array}
$$
(7)式は、 $\hat{a}_k$がすべて独立でないとき、独立でない要因間の影響(共分散)を考慮した式になっています。$\hat{a}_k$がすべて独立の時、分散共分散行列$V$は、対角成分が分散、それ以外の成分(共分散)は0となります。
4-3. 尤度比検定
尤度比検定は、対数尤度比を用いて$\chi^2$分布で検定を行います。対数尤度比は(8)式で表され、漸近的に自由度$r$の$\chi^2$分布となります。
$$
\begin{array}
,G&=-2log;\Bigl(,\frac{L_1}{L_0},\Bigl)\hspace{0.4cm}・・・(8)\
,&\mspace{1cm}\
,&L_0:n個の変数全部を含めたモデルの尤度\
,&L_1:r個の変数を除いたモデルの尤度\
\end{array}
$$
帰無仮説を「$a_{n-r+1} = a_{n-r+2} = \cdots = a_n = 0$」としますと、複数の対数オッズ比($\hat{a}_k$)を同時に検定(有意水準0.05)する式は(9)式となります。
$$
G;\leqq3.84\hspace{0.4cm}・・・(9)\
$$
$\hat{a}_k$が(9)式を満たすとき、仮説は妥当性があるとして採択します。$\hat{a}_k$を一つずつ検定したいときは、(8)式において$r=1$とすればよいです。
4-4. スコア検定
スコア検定は、スコア統計量を用いて正規分布もしくは$\chi^2$分布で検定を行います。スコア統計量は(10)式で表され、漸近的に正規分布となります。
$$
\begin{array}
,&\left. \left.\frac{\partial{L}}{\partial\theta}\right|_{\theta=\theta_0^k} \middle/ SE \right.\hspace{0.4cm}・・・(10)\
\mspace{1cm}\
,&\hspace{0.5cm}L:パラメータが\thetaの(1)式で表されるロジスティック回帰の対数尤度\
\end{array}
$$
$$
\begin{array}
,&\hspace{1cm}\theta:[\hat{b},\hat{a}_1,\hat{a}_2,\cdots,\hat{a}_n]\
,&\hspace{1cm}\theta_0^k:\thetaにおいて、\hat{a}_k=0,で、それ以外のパラメータは最尤推定値\
,&\hspace{1cm}SE:標準誤差\
\end{array}
$$
(10)式から、$a_k=0$を仮説としたときの正規分布における検定(有意水準0.05)を表す式は(11)式となります。
$$
-1.96\leqq,\Bigl( \left. \left.\frac{\partial{L}}{\partial\theta}\right|_{\theta=\theta_0^k} \middle/ SE ,\right. \Bigl) ,\leqq1.96\hspace{0.4cm}・・・(11)\
$$
また、前述のWald検定における(5)式→(6)式→(7)式の変換と同様に、スコア統計量においても、$\chi^2$検定により、複数のスコア統計量($\left. \left.\frac{\partial{L}}{\partial\theta}\right|_{\theta=\theta_0^k} \right.$)を同時に検定することもできます。$a_k=0$を仮説としたときの$\chi^2$分布における検定(有意水準0.05)を表す式は(12)式となります。$\left. \left.\frac{\partial{L}}{\partial\theta}\right|_{\theta=\theta_0^k} \right.$が(12)式を満たすとき、仮説は妥当性があるとして採択します。
$$
\Bigl( \left. \left.\frac{\partial{L}}{\partial\theta}\right|_{\theta=\theta_0^k} \middle/ SE ,\right. \Bigl)^2 ,\leqq,3.84\hspace{0.4cm}・・・(12)\
$$
同様に、複数(r個)のスコア統計量($\left. \left.\frac{\partial{L}}{\partial\theta}\right|_{\theta=\theta_0^{n-r+1}} \right.,\left. \left.\frac{\partial{L}}{\partial\theta}\right|_{\theta=\theta_0^{n-r+2}} \right.,\cdots,\left. \left.\frac{\partial{L}}{\partial\theta}\right|_{\theta=\theta_0^{n}} \right.$)を同時に検定する式(有意水準0.05)は(13)式となります。
$$
\begin{array}
,&\chi^2_L(\phi,0.05)\leqq D^T{V^{-1}}D \leqq\chi^2_H(\phi,0.05)\hspace{0.4cm}・・・(13)\
\mspace{1cm}\
,&;;D=\Bigl[,0,\cdots,0,\left. \left.\frac{\partial{L}}{\partial\theta}\right|_{\theta=\theta_0^{n-r+1}}\right.,,\left. \left.\frac{\partial{L}}{\partial\theta}\right|_{\theta=\theta_0^{n-r+2}}\right.,,\cdots,\left. \left.\frac{\partial{L}}{\partial\theta}\right|_{\theta=\theta_0^n}\right.,\Bigl]\
,&;;V:\left. \left.\frac{\partial{L}}{\partial\theta}\right|_{\theta=\theta_0^k} \right.の分散共分散行列\
,&;;\chi^2_L(\phi,0.05):自由度\phi、有意水準0.05のときの\chi^2分布の下側値\
,&;;\chi^2_H(\phi,0.05):自由度\phi、有意水準0.05のときの\chi^2分布の上側値\
,&;;\phi:自由度(=r)\
\end{array}
$$
4-5. 3つの検定の関係
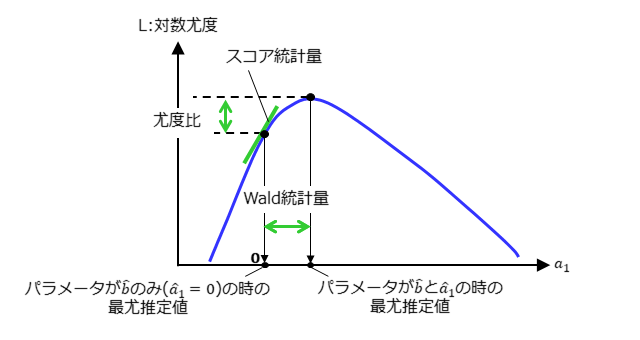
Wald検定、尤度比検定、スコア検定の3つの検定法の位置付けは、よく下図で表されます。ロジスティック回帰のパラメータが、$[,\hat{b},,\hat{a}_1,]$で、$\hat{a}_1=0$を帰無仮説とした検定を行う時を例に示しています。
いずれも、$\hat{a}_1$が0の時と$\hat{a}_1$が最尤推定値の時との差違を評価していることがわかります。Wald統計量は対数オッズ比($\hat{a}_1$)を直接用いて評価していますが、尤度比とスコア統計量は対数尤度関数に関する情報を用いた統計量となっています。いずれの統計量もロジスティック回帰のパラメータ値は最尤推定法で決定することを利用しています。また、Wald統計量と尤度比は、「パラメータが$\hat{b}$と$\hat{a}_1$の時の最尤推定値あるいは尤度」を用いていますが、スコア統計量では「パラメータが$\hat{b}$と$\hat{a}_1$の時のスコア統計量」は0で不変ですので必要ありません。
5. 線形重回帰における検定との比較
線形重回帰との検定の比較をしてみます。線形重回帰式を(14)式に示します。
$$
\hat{y}=\hat{a}_1x_1+\hat{a}_2x_2+\cdots+\hat{a}_nx_n\hspace{1.7cm}・・・(14)\
$$
線形重回帰の検定で一般的なのは、回帰係数$\hat{a}_k$の値が0とすることが妥当か否かを検定することです。$\hat{a}_k$=0のとき、$y$は$x$に対して相関を持たないことになり、線形重回帰を用いることの妥当性がなくなります。(15)式は、線形重回帰における回帰係数$\hat{a}_k$の検定の考え方を示した式です。
$$
-t(\phi,0.05)\leqq \frac{\hat{a}_k}{s・\sqrt{S^{k,k}}} \leqq t(\phi,0.05)\hspace{0.3cm}・・・(15)\
\begin{array}
,&k=1,2,・・・,n\
,&t(\phi,0.05):自由度\phi, 有意水準0.05のときのt分布の値\
,&s^2:yの分散\
,&S^{i,j};xの分散共分散行列の逆行列の(i,j)成分\
\end{array}
$$
Wald検定の(4)式と比較しますと、各パラメータの対応がわかるのではないでしょうか。また、正規分布(t分布)を前提に検定していますので数式の形がよく似ていることがわかります。
6. 補足
線形回帰においては、回帰式($\hat{y}$)の信頼区間の区間推定がありますが、ロジスティック回帰には、それに相当するものはありません。ロジスティック回帰を、正規分布を一般に仮定しないからです。(1)式は、(16)式のように変形できますが、このとき、左辺(目的変数)は、$\hat{y}$が確率を扱うので正規分布には必ずしもなりません。
$$
log(\frac{\hat{y}}{1-\hat{y}})=\hat{a}_1x_1+\hat{a}_2x_2+・・・+\hat{a}_nx_n+\hat{b}\hspace{0.5cm}・・・(16)\
$$
このように、線形式で表すことができて、目的変数の推定値(あるいは残差)に正規分布を仮定しないものを一般化線形モデルと呼びます。一方で、線形回帰など目的変数の推定値(あるいは残差)に正規分布を仮定する場合を一般線形モデルと呼びます。
7. おわりに
今回は、ロジスティック回帰における検定と線形重回帰との関係をおさらいしました。ロジスティック回帰の検定においても、正規分布もしくは$\chi^2$分布の考え方がベースになっていることをご紹介しました。また、同じく正規分布をベースとした線形重回帰における検定との比較もして、ロジスティック回帰の検定と形が良く似ていることを示しました。ロジスティック回帰は、もともとは、ある疾患の発生確率を求めるために創出されたものですが、線形回帰と近いところもあり、両者の相違点が少しはおわかり頂けたら幸いです。
今回も、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから記事を書かせて頂きました。より詳しく知りたいという方は、参考文献などをご参考頂ければと思います。
参考文献
丹後俊郎、山岡和枝、高木晴良:新版ロジスティック回帰分析 SASを利用した統計解析の実際
鶴田陽和:すべての医療系学生・研究者に贈る 独習統計学応用編24講 分割表・回帰分析・ロジスティック回帰