こんにちは、(株)日立製作所 Lumada Data Science Lab. の中川です。普段は人工知能を制御に適用する研究に従事しています。近年、機械学習が注目される中、機械学習理論および機械学習を使った技術開発環境は急速に進歩すると共に、多くの方がデータサイエンスに関わるようになってきました。すでにデータサイエンスに携わっている方や、これからデータサイエンスに関わってみようと思っている方の中で、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから基本的な内容で記事を書きます。今回は、線形単回帰の精度(信頼度)の評価方法についてご紹介します。
プロローグ
あるとき、うちの部署にデータ分析を学びにきている実習生が、線形単回帰の精度を交差検証(CV:Cross Validation)を使って、決定係数を基に、評価しようとしていました。
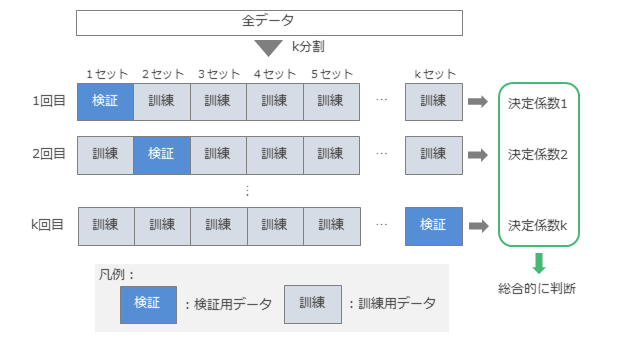
交差検証(CV)のイメージ:
k-分割交差検証:
1回目の評価を次の手順で行います。データをk個のセットに分割します。1セット目からk-1セット目までのk-1セット分のデータで線形単回帰の式を求めます。求めた線形単回帰と残りのkセット目の1セットのデータを使って決定係数の値を求め、その値が1に近いほど、線形単回帰がこの1セットのデータを説明できていると評価します。次に、1セット目と3セット目からkセット目からなるk-1セット分のデータで線形単回帰の式を求め、残りの2セット目のデータを使って、決定係数の値を求め、線形単回帰の説明度合いを評価します。以下、これを繰り返し、各決定係数の値から当該データを線形単回帰で説明する場合の汎化性が高いと推測します。
私:なぜCVをしているのかな?
実習生:えっ…精度評価といったらCVなんじゃないでしょうか。
私:CVもいいけど、他にも、統計学で扱う推定でも精度評価はできるんですよ。ただし、条件はつくけど。
実習生:どういうことでしょうか。
線形単回帰とは
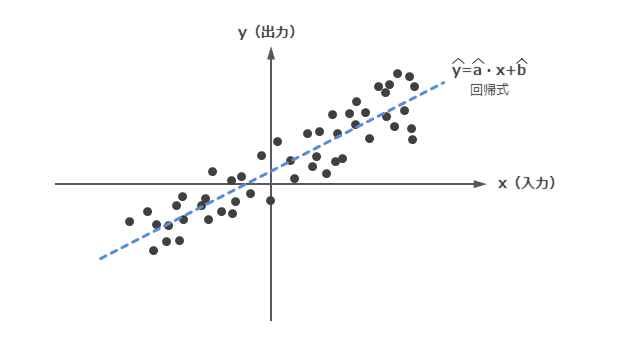
あらためて、線形単回帰のおさらいを簡単にします。
線形単回帰とは、x軸とy軸の平面上に分布している点(データ)に対して、もっとも当てはまるように直線を引くものです。具体的には、直線の傾き(a)と切片(b)は、直線と点(データ)のy軸方向の誤差の二乗和が最小となるように決めます。直線からy軸方向へのデータの分散が最小となるように、aとbの値を決めると言い換えることもできます。
上記の方法で決めたこの直線(回帰式)はどの程度、信頼できるものなのでしょうか。上述しましたように、決定係数は、その値が1に近いほど、検証に用いたデータを線形単回帰が説明できていると判断はできます。しかし、決定係数の値から直接、線形単回帰の信頼性を解釈するのは、難しいと感じたことはないでしょうか。機械学習全般に言えることですが、データを使って、機械学習(ここでは直線)のパラメータ値(ここでは傾き(a)と切片)を決めたとき、その機械学習は、(可能であれば)将来に渡ってどの程度信頼できるものなのかを、理論的かつ定量的に確認しておくことは、サービスや製品の信頼性を担保する観点で重要と考えています。そこで、交差検証を用いた決定係数の評価に加えて、同じく統計学で扱う推定について、あらためて紹介したいと思います。
精度評価の方法を考える
統計学で扱う推定で線形単回帰の信頼度を評価するための条件を述べます。
信頼度を評価するための条件条件:
-
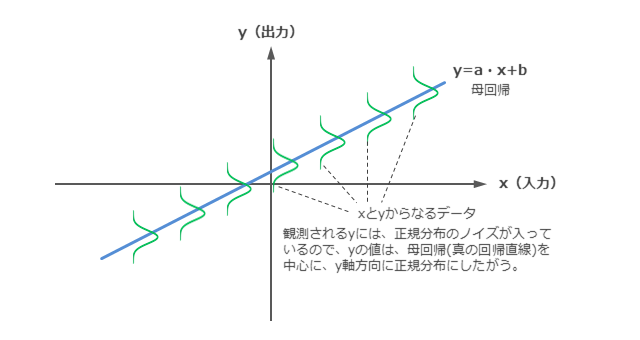
「x」と「yからノイズを除去した値(yの真値)」の関係が線形であること。
-
yに入っているノイズが正規分布であること。
-
ノイズの分散も任意のxで同じであること。
-
xには、ノイズが入っていないこと。
現実的には、厳しい条件かもしれませんが、この条件を満たせば、正規分布における区間推定の手法が使えるようになり、線形単回帰の信頼度を定量的に評価できるようになります。
統計学で扱う推定(区間推定):
線形単回帰の信頼度を評価する方法として、区間推定があります。区間推定の式は、次の(1)式で与えられます。
$\hspace{0.5cm}\hat{y}_k-(t(φ,α)・\sqrt{s^2/h _{kk}}) ≦y≦ \hat{y} _k+(t(φ,α)・\sqrt{s^2/h _{kk}}) ・・・(1)$
$\hspace{1cm}\hat{y} _k= \hat {a}・x _k+\hat {b} $
$\hspace{1cm}x_k:信頼区間を評価したいy_kに対応するxの値$
$\hspace{1cm}t(φ,α):自由度φ, 信頼区間を指す値αから決まるt分布の値$
$\hspace{1cm}1-α:信頼係数$
$\hspace{1cm}s^2:分散$
$\hspace{1cm}h_{kk}=1/n+{(x_k-\bar{x})^2/Σ(x_i-\bar{x})(x_i-\bar{x})}:てこ比$
(1)式で表される線形単回帰の区間推定の式は、正規分布の区間推定を線形単回帰に拡張したもので、(1)式で示される区間にy(ノイズを除去した後の真のyの値)が100・(1-α)%の確率で収まることを指します。このように、(1)式を使えば、100・(1-α)%の信頼区間を定量的に求めることができ、線形単回帰の信頼度を定量的に表すことができます。(1)式の導出、意味については、今回は省略致しますが、ご興味のある方は、ご質問頂いても良いですし、あるいは、参考文献などを参照して頂くのも良いかと思います。
長所・短所を考える
交差検証による決定係数値で線形単回帰の信頼度を評価する場合と、今回紹介した統計的推定で評価する場合の長所・短所を表にまとめてみました。
| 方法 | 交差検証(CV) | 統計学で扱う推定 |
|---|---|---|
| 長所 | ノイズの分布が正規分布でなくても 精度評価ができる。 |
線形単回帰を使って予測する前に、ど の程度、信頼できるか定量的に把握で きる。 |
| 短所 | ノイズの分布が不明なので、保有し ているデータ内でしか性能が保証で きない。 |
ノイズの分布が正規分布、任意のxに 対して分散が等しい、の条件がある。 |
なお、プロローグでは、決定係数値の評価に交差検証を用いていますが、決定係数の評価に交差検証は、必ずしも必要ではありません。また、決定係数値の評価と今回紹介しました推定の両方を用いて、線形単回帰の評価を行うことも、線形単回帰の信頼性を評価するのに有効です。
まとめ
機械学習においては学習したモデルの精度評価に、交差検証を用いて決定係数で評価することがあるかと思いますが、線形単回帰の精度・信頼度の評価方法として、今回紹介した方法もあることを知っておくと、適用対象に応じて、より適切な評価方法を選ぶことができるのではないでしょうか。いろいろな理論・方法を知っておくとデータサイエンティストとしての幅も広がるかと思います。正規分布を仮定している理論・方法は、いろいろあります。また、世の中の正規分布になっている現象もあります。正規分布を仮定している理論・方法、正規分布となっている現象を探してみるのも、さらに知見が広がって、おもしろいかもしれません。今回は、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから記事を書かせて頂きました。より詳しく知りたいという方は、参考文献などをご参考頂ければと思います。
参考文献
東京大学教養学部学部統計学教室編,統計学入門
永田靖著,入門統計解析法