こんにちは、(株)日立製作所 Lumada Data Science Lab. の中川です。普段は人工知能を制御に適用する研究に従事しています。近年、機械学習が注目される中、機械学習理論および機械学習を使った技術開発環境は急速に進歩すると共に、多くの方がデータサイエンスに関わるようになってきました。すでにデータサイエンスに携わっている方や、これからデータサイエンスに関わってみようと思っている方の中で、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから基本的な内容で記事を書きます。今回は、フーリエ解析のおさらいをします。
1. はじめに
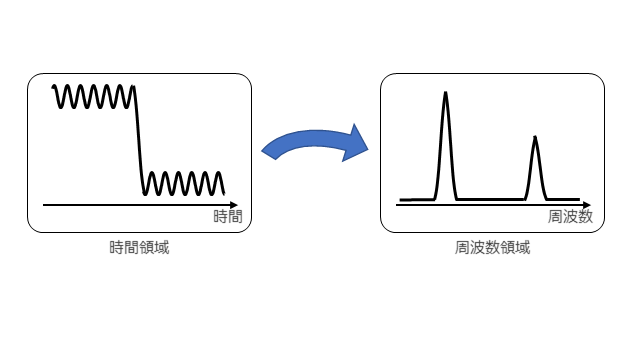
時間領域(時系列波形)では、とらえにくい特徴でも周波数領域に移してみると、みえてくる特徴があります。フーリエ解析は、時間領域の情報を情報量を落とさずに、周波数領域に移して解析する手法です。以下の順で、フーリエ解析のおさらいをします。
・フーリエ級数:三角関数を用いた表現
・フーリエ級数:複素数を用いた表現
・フーリエ変換と離散フーリエ変換
2. フーリエ級数:三角関数を用いた表現
(1)~(3)式は、三角関数を用いたフーリエ級数の式を示しています。
$$
\begin{align}
f(t)&=\frac{a_0}{2}+\sum_{n=1}^{\infty}(a_ncos(n\omega_0t)+b_nsin(n\omega_0t)){\quad}・・・(1)\
a_n&=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)cos(n\omega_0t)dt\hspace{3.55cm}・・・(2)\
b_n&=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)sin(n\omega_0t)dt\hspace{3.3cm}・・・\hspace{0.2cm}(3)\
\omega_0&=\frac{2\pi}{T}:基準周波数
\end{align}
$$
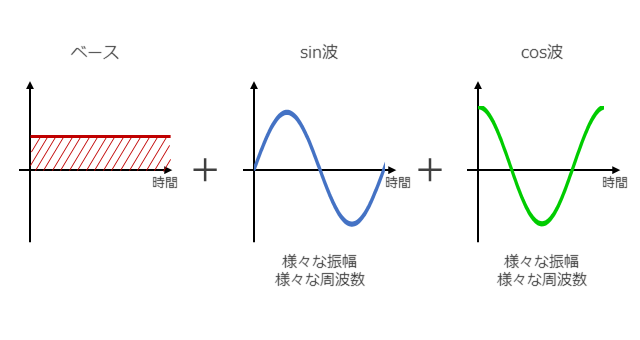
(1)式から、関数$f(t)$は、定数項と$cos$関数の項と$sin$関数の項に分解できることがわかります。下図は、三角関数を用いたフーリエ級数による分解のイメージを示しています。定数項は、ベースの部分(0Hzの部分と言っても良いかもしれません)を表現しています。$cos$関数の部分は、$a_n$が$cos$波の様々な振幅を表現し、$n$が$cos$波の様々な周期を表現します。同様に、$sin$関数の部分は、$b_n$が$sin$波の様々な振幅を表現し、$n$が$sin$波の様々な周期を表現します。この組み合わせで、周期$T$の任意の時系列波形が表現できます。
3. フーリエ級数:複素数を用いた表現
(4)式と(5)式は、複素数を用いたフーリエ級数の式を示しています。
$$
\begin{align}
f(t)&=\sum_{n=-\infty}^{\infty}c_{n}e\hspace{0.05cm}^{in\omega_0t}\hspace{4cm}・・・(4)\
c_n&=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)\hspace{0.05
cm}e\hspace{0.05cm}^{-in\omega_0t}dt\hspace{0.05cm}\hspace{2.39cm}・・・(5)\
\end{align}
$$
複素数を用いると(1)式で示した3つの項を一つにまとめられます。(6)式は、オイラーの公式と言われる式で、複素数を用いることで$cos$関数と$sin$関数を$exp$関数にまとめられることがわかります。
$$
e^{in\omega_0t}=cos(n\omega_0t)+i・sin(n\omega_0t)\hspace{1.2cm}・・・(6)
$$
また、$c_n$と($a_n$, $b_n$)の関係は、(7)式と(8)式となります。同じく、$a_n$と$b_n$を$c_n(c_{-n})$にまとめられています。
$$
\begin{align}
c_n&=\frac{1}{2}(a_n-ib_n)\hspace{3.8cm}・・・(7)\
c_{-n}&=\frac{1}{2}(a_n+ib_n)\hspace{3.8cm}・・・(8)\
\end{align}
$$
(4)式は、(1)式に(6)式を代入することで得られますが、逆に(4)式を以下のように変形してみます。
$$
\begin{align}
f(t)&=c_0+\sum_{n=1}^{\infty}c_{n}e\hspace{0.05cm}^{in\omega_0t}+\sum_{n=-1}^{-\infty}c_{n}e\hspace{0.05cm}^{in\omega_0t}\hspace{1cm}・・・\hspace{0.2cm}(9)\
&=c_0+\sum_{n=1}^{\infty}c_{n}e\hspace{0.05cm}^{in\omega_0t}+\sum_{n=1}^{\infty}c_{-n}e\hspace{0.05cm}^{-in\omega_0t}\hspace{10.4cm}\
&=\frac{a_0}{2}+\sum_{n=1}^{\infty}\frac{1}{2}(a_n-ib_n)(cos(n\omega_0t)+i・sin(n\omega_0t))\
&\hspace{1.3cm}+\sum_{n=1}^{\infty}\frac{1}{2}(a_n+ib_n)(cos(n\omega_0t)-i・sin(n\omega_0t))\hspace{5.3cm}\
&\hspace{3cm}・\
&\hspace{3cm}・\
&\hspace{3cm}・\
&=\frac{a_0}{2}+\sum_{n=1}^{\infty}\frac{1}{2}{(a_ncos(n\omega_0t)+b_nsin(n\omega_0t))-i(b_ncos(n\omega_0t)-a_nsin(n\omega_0t))}\hspace{0.8cm}\
&\hspace{1.3cm}+\sum_{n=1}^{\infty}\frac{1}{2}{(a_ncos(n\omega_0t)+b_nsin(n\omega_0t))+i(b_ncos(n\omega_0t)-a_nsin(n\omega_0t))}\
&\hspace{13cm}・・・\hspace{0.2cm}(10)\
\end{align}
$$
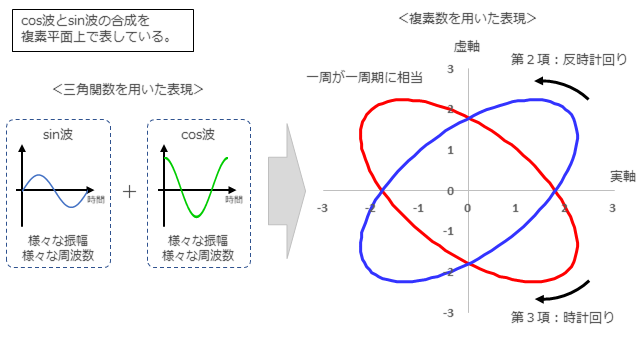
(10)式の第2項の実部と第3項の実部が足されて残り、第2項の虚部と第3項の虚部は足されて打ち消されて、(1)式が得られることがわかります。下図は、複素数を用いたフーリエ級数のイメージを示しています。(10)式の第2項の値と第3項の値は、複素平面上の楕円上を反時計回りと時計回りに回ることで、虚部を相殺し、実部だけが残ります。反時計回りは正の周波数であり、時計回りは負の周波数とも言えます。なお、楕円の形は、$a_n,b_n$の値に応じて変わります。
なお、(9)式における$c_0$は、(5)式より$f(t)$を$-(T/2)$から$T/2$まで積分して$T$で割った値、すなわち、$f(t)$の平均値で、(1)式における$a_0/2$に等しくなります。この値は、実数なので、上図では、実軸上の点となります。各周波数の数だけ、原点を中心とする反時計回りと時計回りの一対の楕円が存在し、$f(t)$は、その一対の楕円とベース部分の点の合成というイメージを持つとわかりやすいかもしれません。
4. フーリエ変換と離散フーリエ変換
4-1. フーリエ変換
前章で述べましたフーリエ級数は、時間領域の周期関数$f(t)$を三角関数もしくは複素数を用いて表しました。フーリエ変換とは、時間領域の関数($f(t)$)を周波数領域の関数($F(\omega)$)に変換するものです。(5)式において$\omega_0$の値を$-\infty$から$\infty$まで連続の値として拡張したときの$c_n$の値を求める、と考えるとわかりやすいかもしれません。$F(\omega)$は(11)式で与えられます。(11)式にありますように、複素平面上の単位円周上に沿って、$f(t)$を積分した結果です。単位円一周が一周期($2\pi/ω$)に相当します。$ω$の値に応じて、単位円を周回する回数が変わることがわかります。
$$
F(\omega)=\int_{-\infty}^{\infty}f(t)\hspace{0.05
cm}e\hspace{0.05cm}^{-i\omega{t}}dt{\quad}・・・(11)\
$$
また、(11)式は、$f(t)$と$e^{-i{\omega}t}$の内積を計算しているとも解釈できます。(6)式で示しましたように、$e^{-i{\omega}t}$は、$cos({\omega}t)$と$sin({\omega}t)$に分解できますので、(11)式は、$f(t)$と$cos({\omega}t)$の内積、$f(t)$と$sin({\omega}t)$の内積をそれぞれ求めていると言えます。この演算は、三角関数の直交性から、$cos({\omega}t)$成分(複素平面上の実軸成分に相当)と$sin({\omega}t)$成分(複素平面上の虚軸成分に相当)を抽出していると言えます。
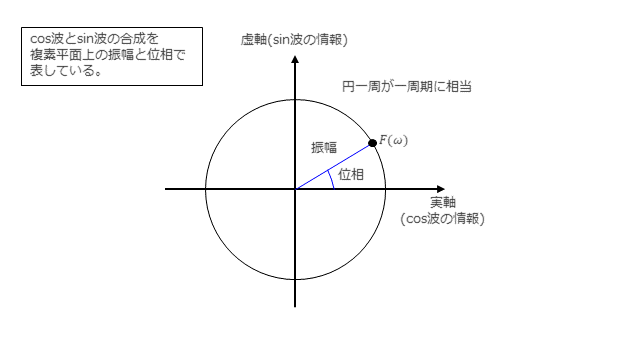
下図は、フーリエ変換した結果($F(\omega)$)のイメージを示しています。$F(\omega)$は複素数で、複素平面上の円周上の値となり、$\omega$における振幅(|$F(\omega)$|)と位相(${\angle}F(\omega)$)を表します。
前章で説明しましたように、複素数を用いたフーリエ級数では、反時計回り(正の周波数)と時計回り(負の周波数)の1組の周波数で表しましたので、フーリエ級数に当てはめれば($f(t)$がフーリエ級数で表されるとき)、$\omega$における振幅(|$F(\omega)$|)は(12a)式および(12b)式となり、位相(${\angle}F(\omega)$)は、(13a)式および(13b)式となります。
$$
\begin{align}
|F(\omega)|&=\frac{1}{2}\sqrt{a_n^2+b_n^2}\hspace{2.35cm}・・・(12a)\
|F(-\omega)|&=\frac{1}{2}\sqrt{a_n^2+(-b_n)^2}\hspace{1.35cm}・・・(12b)\
\angle|F(\omega)|&=\tan^{-1}(\frac{b_n}{a_n})\hspace{2.6cm}・・・(13a)\
\angle|F(-\omega)|&=\tan^{-1}(\frac{-b_n}{a_n})\hspace{2.25cm}・・・(13b)\
\end{align}
$$
なお、(11)式は、(4)式に(5)式を代入して、$T$→$\infty$とすることで得られます。(11)式において、$T$→$\infty$としていますので、$f(t)$は、有限の周期を持つ関数すなわち周期関数である必要はありません。
4-2. 離散フーリエ変換
離散フーリエ変換とは、値がとびとびになっているときに用いるフーリエ変換です。考え方は、フーリエ変換と同じですが、実データは一般に離散値ですので、実データにフーリエ変換を適用する場合は、離散フーリエ変換を用いることになります。(14)式は、離散フーリエ変換の式です。
$$
\begin{align}
F(n)&=\frac{1}{N}\sum_{j=0}^{N-1}f(j)\hspace{0.05cm}e\hspace{0.05cm}^{-i2\pi{n\frac{j}{N}}}\hspace{2.1cm}・・・(14)\
n&:0,1,・・・,N\hspace{0.5cm}周波数番号\
j&:0,1,・・・,N\hspace{0.5cm}データ番号\
\end{align}
$$
前節で(5)式において$\omega_0$の値を$-\infty$から$\infty$まで連続の値として拡張したときの$c_n$の値を求めることが、フーリエ変換と紹介しましたが、離散フーリエ変換では、(5)式の$\omega_0t$を離散値である$2{\pi}j/N$に置き換えて、関数$f$の値の個数が無限から有限($N$個)とすることで得られます。なお、円一周が一周期に相当することは、フーリエ変換と同じです。(14)式において$n$の値に応じて、単位円を周回する回数が変わることがわかります。$F(n)$は複素数で、複素平面上の円周上の値となり、周波数番号$n$における振幅(|$F(n)$|)と位相(${\angle}F(n)$)を表します。なお、$F(n)$は、高々、データ数しか得られませんが、反時計回り(正の周波数)と時計回り(負の周波数)の1組の周波数で表しますので、実質的に得られる$F(n)$は、(データ数/2)もしくは(データ数/2-1)となります。
5. おわりに
今回は、フーリエ解析のおさらいをしました。できるだけ、直感的に理解できるように数式と図をリンクさせて説明することを心がけました。フーリエ解析のイメージがうまくつかめたという方がいらっしゃれば幸いです。冒頭でも述べましたが、一般に時間領域と周波数領域は表裏一体の関係にあります。フーリエ解析(特にフーリエ変換)は、時間領域では、とらえにくい特徴を周波数領域に移すことで、みえやすくするあるいは扱いやすくする手法とも言えます。フーリエ解析を使ったことがない方がいらっしゃれば、機会がありましたら、ぜひ使ってみて下さい。
今回も、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから記事を書かせて頂きました。より詳しく知りたいという方は、参考文献などをご参考頂ければと思います。
参考文献
大石進一:フーリエ解析
金谷健一:これなら分かる応用数学教室
トランスナショナル カレッジ オブ レックス:フーリエの冒険