1. はじめに
みなさんはじめまして!
競技プログラミングにハマっている Ryusuke と申します。
本日は @kanten4205 さんが作成した 競プロアドベントカレンダー2021 にて競技プログラミングの記事を書くことになったので、投稿しました。
Python, AtCoder, 始めたばかり
この 3 つのいずれかに該当する方は 絶対に 読んでください!!
この記事を読んでいただければ必ず何かを得られると思います!
1-1. 自己紹介
まずは私の自己紹介をしたいと思います。
所属:公立はこだて未来大学システム情報科学部 B3
趣味:競技プログラミング、バスケットボール、ピアノ、競技数学
AtCoder:https://atcoder.jp/users/ryusuke_h
Twitter:https://twitter.com/ryusuke__h
GitHub:https://github.com/ryusuke920
はてなブログ:https://ryusuke920.hatenablog.jp
OMC:https://onlinemathcontest.com/users/ryusuke_920
Qiita:https://qiita.com/ryusuke920
ざっくりとこんな感じです。
特にTwitterには365日浮上していますので、良ければフォローよろしくお願いします^^
1-2. 本記事の内容について
今回は競技プログラミングを始めたばかりという人向けに記事を書くことにしました。
最近、Twitterをしていると毎週のように競技プログラミングを始めた方から、コードに対する質問が来たり、何から始めれば良いですか、という質問をいただきます。
個人的には競技プログラミングはここ数年で急激に様々なコンテンツが増えたため、始めやすくなっていると思っていたのですが、かえってわからない方も多いみたいです。
なので、そんな方向けに今回は記事を書いていますので、ぜひ初心者の方や始めたばかりの方は読んでみてください。
2. 競技プログラミング
競技プログラミングは、出題された課題を解決するプログラムをいかに速く正確に記述出来るかを競うプログラミングコンテストです。
主な参加者はエンジニアはもちろんのこと、数学やパズルが好きだったり得意な方にもオススメです。
私の周りでは中高生で参加している学生さんもたくさんいます。
一般的には出題された問題の正解数が多い人が勝ち、同率の場合はいかに早く解けたかで順位が決まります。
実際に、文章で説明してもわかりづらいと思うので個人的にオススメの YouTube 動画を載せておきます。
こちらの動画は今年3月にテレ東BIZさんにてアップされた動画であり、初心者で競技プログラミングを始めた方が実際にコンテストに出て問題を解くという動画です。
競技プログラミングについての説明も詳しくされているので興味のある方はぜひ見てみて下さい。
3. AtCoder
続いては AtCoder についての紹介です。
AtCoder とは、日本で最大級の競技プログラミングサイトです。
3-1. AtCoder について
詳細については AtCoder 株式会社代表取締役社長の 高橋直大 さんが下記のように説明しているので引用します。
AtCoderは、プログラミングのコンテストを開催している企業です。「もの作りのアイデアを競う」だとか、「製品を作る」という部分から少し乖離した、「複雑な処理を正しく記述する」だったり、「計算時間のかかる処理を、数学的/情報科学的にスマートに処理する」だったりを競うコンテストになります。多くの人が参加できるようにするため、専門分野に対する知識等は出題されず、ベースとなるアルゴリズムに関する問題が出題されます。コンテストは毎週開催され、10000人ほどが同時に参加しております。
採点は完全に機械的に行われ、想定通りの答えが出力されていれば正解となります。人間の好みに左右されることがない、確かな評価となります。
このようなコンテストであるため、エンジニアに必要な、全ての能力が測定できるわけではありません。必要な項目は、以下の資料(AtCoderの営業資料の一部)をご確認ください。
以上が AtCoder についての引用になります。
アカウントを登録すると、すぐにコンテストに参加できるので未登録の方はぜひ登録してみて下さい。
3-2. AtCoder の色・レートについて
AtCoder はレートごとに色がついています。
色についての評価は以下のようになります。
こちらについても上記の chokudai さんのブログを要約しています。
| レート | 色 | 実力 |
|---|---|---|
| Rating - 399 | 灰 | 1回参加するだけでなれるので実力の保証は全くない |
| 400 - 799 | 茶 | AtCoder 内だとあまり高くはないが一般的には十分なレベル |
| 800 - 1199 | 緑 | 学生ならかなり優秀 / エンジニアとしてもある程度の安心感がある |
| 1200 - 1599 | 水 | 半数以上のIT企業において、アルゴリズム能力についてはカンスト |
| 1600 - 1999 | 青 | アルゴリズム力はカンストしており、一部企業においては持て余してしまう |
| 2000 - 2399 | 黄 | 研究職・研究開発などや、高度なアルゴリズムを要求される開発現場で重宝される |
| 2400 - 2799 | 橙 | 検索サービスなどの滅茶苦茶アルゴリズムが大切な会社・研究開発でないとアルゴリズム力を活かせない |
| 2800 - | 赤 | 化け物しかいない / chokudai社長はここです |
銅王冠・銀王冠・金王冠といったランクも赤の上にありますが、今回は説明を省略します。
この表だけを見ると、真ん中くらいが水・青に見えてしまい、灰・茶・緑だと強くないと思われがちですが、茶の紹介でもあるように、 AtCoder 内では低いだけで一般的には十分すごく、通用すると思います。
私自身は緑の真ん中くらいをうろついています。
レートを上げていくことはとても大変な道ですが、勉強を重ねてレートが上がったときはとても嬉しいです。
AtCoder について紹介し終えたところで今回のタイトルにもある通り、 Python で始めた方向けに次章では標準入出力を紹介します。
競技プログラミングを行う上で標準入出力は必須知識であり、躓きやすいポイントです。しっかりと確認していきましょう。
4. Pythonの標準入出力について
競技プログラミングを始めるにあたって、ほぼ全ての問題は入力を受け取ってそれに対する出力をするのが一般的なので、まずは Python における標準入出力の説明をします。
4-1. 1行1列の入力を受け取る場合
入力
$N$ (文字列もしくは数字)
コード
# 文字列を受け取る場合
S = input()
# 整数を受け取る場合
N = int(input())
# 小数を受け取る場合
F = float(input())
input()で入力を受け取ると、str型として入力を受け取ることができます。
さらに、整数で受け取りたい場合は int(input()) で受け取ります。
1行1列の入力場合は大半がこの2つで済みますが、場合によっては 小数で受け取りたい場合もあります。
その際には float(input()) とすることで入力を受け取ることができます。
4-2. 1行複数列の入力を受け取る場合
2つの入力
$A \quad B$ (2つの文字列)
3つの入力
$X \quad Y \quad Z$ (3つの整数)
3つの入力
$H \quad M \quad S$ (3つの小数)
と言った場合の入力を行いたい場合
コード
# 文字列を受け取る場合
A, B = input().split()
# 整数を受け取る場合
X, Y, Z = map(int, input().split())
# 小数を受け取る場合
H, M, S = map(float, input().split())
全ての入力の受け取りに出てくる.split()は()の中に文字を入れることでその文字区切りで入力を受け取ります。
何も設定していない今回のような場合はデフォルトで空白扱いになるので、A B と言ったように空白区切りで入力を受け取りたい場合に関しては.split()が必要なことを覚えておきましょう。
4-3. 1行の配列を受け取る場合
入力
$ A_1 \quad A_2 \quad A_3 \quad ... \quad A_N $
コード
# 文字列を受け取る場合
A = input().split()
# 整数列を受け取る場合
A = list(map(int, input().split()))
# 小数列を受け取る場合
A = list(map(float, input().split()))
list型として、 【4-2. 1行複数列の入力を受け取る場合】 で紹介したコードを list()で囲むことで入力を受け取ることが可能となります。
4-4. 複数行複数列の入力を受け取る場合
入力
$ A_{1,1} \quad A_{1,2} \quad A_{1,3} \quad ... \quad A_{1,N} $
$ A_{2,1} \quad A_{2,2} \quad A_{2,3} \quad ... \quad A_{2,N} $
...
$ A_{N,1} \quad A_{N,2} \quad A_{N,3} \quad ... \quad A_{N,N} $
# 複数行の文字列を受け取る場合
A = [input().split() for _ in range(N)]
# 複数行の整数列を受け取る場合
A = [list(map(int, input().split())) for _ in range(N)]
# 複数行の小数列を受け取る場合
A = [list(map(float, input().split())) for _ in range(N)]
ここが少し難しいポイントかもしれません。
上記の3つの受け取り方のコードはいずれも内包表記と呼ばれる書き方をしています。
これは、全体のリストの中に N 回 for 文を回したものを受け取ったものを入れています。
Python ではこの内包表記をよく使うので必ず覚えておきましょう。
標準入出力の説明は以上になります。
この後は実際にABCの過去問を用いてどのように問題を解いていくのか解説してきたいと思います。
5. ABCの解説
AtCoderと標準入出力を教えた所で実際に直近のABCの問題を解説します。
まずはじめに、AtCoder に存在するコンテストの種類について説明します。
知らないと思っていたのと違う、と思ってしまうこともよくあるのでこの際に知っておきましょう。
5-1. AtCoderのコンテストの種類
そもそもAtCoderには大きく分けて現在 4 種類のコンテストが存在しています。
| コンテスト名 | レート対象 |
|---|---|
| ABC (AtCoder Beginner Contest) | 0 - 1999 |
| ARC (AtCoder Regular Contest ) | 0 - 2799 |
| AGC (AtCoder Grand Contest) | 1200 - inf |
| AHC (AtCoder Heuristic Contest) | 全ユーザー |
それぞれのコンテストについて下記で詳しく説明していきます。
5-1-1. ABC(AtCoder Beginner Contest)
まずはABCについてです。
こちらは先ほどから何回か出てきていますが、AtCoderにおいて最も初心者向けのコンテストとなっています。
参加するために必要なレート制限もなく、問題は A 〜 H までの 8 問構成となっています。
なので、 AtCoder に登録を終えて実際にコンテストに出たいと言う方はまずはこの ABC に参加するのが良いと思います。
直近だと M-SOLUTIONS プロコンオープン2021(AtCoder Beginner Contest 232) が明後日開催されるのでぜひ参加してみて下さい!
最近のコンテストはスポンサーが多く、ABCの前にスポンサー名が入っていることはよくあります。有名になってきてる証拠ですかね?嬉しいです!!
今章ではこちらの初心者向けのコンテストの A 〜 C の 3 問を後ほど解説します。
最近までは A 〜 F までの 6 問構成でしたが、問題数が少なく1問1問に差があるなどということからABC212以降 8 問構成になりました。
5-1-2. ARC(AtCoder Regular Contest)
続いてはARCです。
こちらは、ABCよりも難易度が上がっているコンテストとなります。レート制限こそはありませんが始めたての方だと1問も解けないと言うことはよくある話なので、まずはABCで慣れてから出場するのをオススメします。
最近のARCの傾向としては数学問題が出ているイメージが個人的には強いです。ですので、数学が好きな方やパズルが好きな方は出場してみるのもオススメです!
5-1-3. AGC(AtCoder Grand Contest)
続いてはAGCです。
このコンテストは、最も難易度の高いコンテストとなっています。レート制限も 1200 -となっており、とても難しい問題となっています。
自分も rated でこのコンテストに出るのがずっと夢なので来年までには叶えたいです。
初心者の方は、1問解けるか解けないかレベルの問題です。
参考までに、直近で開催された AGC の1問目を紹介しておきます。
この問題は難易度がいわゆる水 diffとなっております。
これは水のレート帯の方が2人に1人解けるかどうかというレベルということを表しています。
難しい!!
特別アルゴリズムが必要というわけではなく、どちらかというと数学・パズル寄りの問題になっていますので、興味のある方は挑戦してみて下さい!
5-1-4. AHC(AtCoder Heuristic Contest)
最後に紹介するのは、AHCというコンテストです。
これはいわゆるマラソン型と呼ばれるコンテストで、AtCoderにて新たに定期的に開催されるプログラミングコンテストです。
ABC / ARC / AGC などのアルゴリズムコンテストと異なり、最適解を出すのが難しい問題に対し、出来るだけ良い解を作成するコンテストとなります。
開催期間も ABC / ARC / AGC などは高々2,3時間程度ですが、こちらは1週間や1ヶ月などとかなり長期のコンテストとなっています。
問題文もとても複雑でいかに点数を伸ばせるかがポイントです。また、 ABC / ARC / AGC のレートとは異なり、新しいヒューリスティック部門用のレートが付与されています。
レートの評価形式もアルゴリズムコンテストとは異なり、成績が悪くても下がることはありません。一番良い成績でレートが伸びていくのでベストパフォーマンスが評価される形式となっています。
アルゴリズムコンテストは苦手だが、このマラソン型のコンテストは好き・得意という方はよくいます。
興味のある方はまずは過去問を解いてみましょう!
第1回のAHCの問題を以下に貼っておきます。
5-2. ABC-A 解説
まずは直近5回の ABC-A 問題を解説したいと思います。
これが AtCoder 上で最も簡単な問題になります。
頑張って理解して行きましょう!
ABC231-A - Water Pressure
はじめに解説する問題は今週に行われた A 問題です。
これは水深を入力として受け取り、そこでの水圧を出力する問題です。
水深 $x[m]$ の場所では $ \frac{x}{100} [MPa]$になるので、受け取った値を 100 で割ることで答える事ができます。
Python で出力を行う際には print() で可能です。
d = int(input())
print(d / 100)
ABC230-A - AtCoder Quiz 3
条件分岐は if 文で行う事ができるので覚えましょう。
ただこの問題のややこしい所は、3桁での出力をしなければならないので、答えが2桁以下の際には 0 で埋める必要があります。
この方法については色々ありますが、今回はフォーマット済み文字列リテラルによる出力の行い方を記述します。
フォーマット済み文字列リテラルについてはこちらの記事が参考になりますので知らない方は一読してみてください。
https://docs.python.org/ja/3.8/tutorial/inputoutput.html#tut-f-strings
こちらを使用し、 :0n とすると、n桁表記に満たない場合は0で補ってくれます。
今回の場合は3桁表記の指定なので、 :03 としましょう。
n = int(input())
if n >= 42:
print(f"AGC{n + 1:03}")
else:
print(f"AGC{n:03}")
ABC229-A - First Grid
続いての問題は探索問題です。
まず、入力として $2 \times 2$ のマス目が与えられます。
#上のみを動く事ができ、与えられた入力に関してどの2つの黒マス同士も行き来できるかどうかを判定する問題です。
これは競技プログラミングに慣れていない方は中々戸惑うのではないでしょうか?
今回の解くポイントは入力が高々4マスしかないことです。
さらに制約で2マス以上に # が入っていることが保証されています。
まずは簡単な全てが # の場合を考えてみましょう。このときは言うまでもなく行き来できるので Yes になります。
続いて3つが # のときを考えてみましょう。
考えられる候補は以下の4通りです。
. # $\qquad$ # . $\qquad$ # # $\qquad$ # #
# # $\qquad$ # # $\qquad$ # . $\qquad$ . #
これは全ていけることがわかります。
迷った場合にはこのように具体例を考えるとイメージがつくことが多々あります。
では最後に2つのみが # の場合を考えてみましょう。
ここまでの考え方を踏まえて、上下もしくは左右に2つある場合は問題なく行き来できることがわかってきたと思います。
なので行き来できないパターンは以下の対角に位置している2パターンのみである事がわかります。
# . $\qquad$ . #
. # $\qquad$ # .
したがって、答えの大半が Yes なので、 Noのときだけ if 文で場合分けを行いましょう。
サンプルコードは以下のようになります。
s1 = input()
s2 = input()
if (s1 == ".#" and s2 == "#.") or (s1 == "#." and s2 == ".#"):
print("No")
else:
print("Yes")
ABC228-A - On and Off
これもまたクセのある問題です。
ここ最近のABC-Aはとても難しく感じますね...
電気をつけている時間帯かどうかを判定する問題です。
この問題の何が厄介かというと、入力 $S, T$ に対して、大小関係が与えられてないことです。
つまり $S > T$ の場合も入力としては十分に考えられると言うことです。
まずは簡単な $S < T$ を考えてみましょう。
これは少し考えれば見えてきますよね。
$S \leqq X < T$ であれば答えは Yes になります。
では $S > T$ の場合はどのようになるでしょうか。
簡単に考えるポイントは大小関係が逆のときは逆で考えると言うことです。
どう言うことかというと、$S > T$だった場合でも、 $S < T$ として入れ替えて考えます。
そしてこの状態で上記の考え方と同じように if 文で判定を行います。
すると、答えも逆になるので Yes のときに No , No のときに Yes とすることで正解する事ができます。
サンプルコードは以下のようになります。
s, t, x = map(int, input().split())
if s < t:
print("Yes") if s <=x < t else print("No")
else:
s, t = t, s
print("No") if s <= x < t else print("Yes")
ABC227-A - Last Card
これは本当に難しく感じたA問題です。
先ほども言いましたが、最近の A 問題は個人的にとても難しく感じます...
$K$ 枚のトランプが最終的に誰に配られるのかと言う問題です。
for 文で1枚ずつ誰に配っていくのかを考えていく方法がシンプルではないですが、安全だと思います。
シンプルに実装するのも重要ですが、確実にバグらせないコードを書くことも競技プログラミングにおいてはとても重要です。
割り切れる際には 0 番目の人は存在せずに n番目の人になる点だけ注意しましょう。
サンプルコードは以下のようになります。
n, k, a = map(int, input().split())
ans = []
for i in range(a, a + k):
if i % n == 0:
ans = n
else:
ans = i % n
print(ans)
今は for 文でぶん回して正解するコードを紹介しましたが、数学的に以下のように解くこともできるのでよければ参考にしてください。
n, k, a = map(int,input().split())
ans = (a + k - 1) % n
if ans == 0:
print(n)
else:
print(ans)
5-3. ABC-B 解説
ここからはB問題の解説です。
A -> Bにかけて増えることは、 for 文がとても必要になってきたりします。
他にも問題文自体がややこしくなっていくことがあります。
しっかりと 5 問おさえていきましょう。
ABC231-B - Election
1 問目は投票数の一番多い人の名前を出力する問題です。
これは現実的にもとても必要な場面はよくありそうですし良問ですね。
このように、〇〇が△票のような実装に対しては、 Python 標準ライブラリである collections の Counter クラスを使うと、出現回数が多い順に要素を取得できます。
詳しい利用方法についてはこちらの記事を参照ください。
https://note.nkmk.me/python-collections-counter/
今回はこの Counter を使用することで、投票数を調べることができます。
AtCoder ではこのような場面が頻出なので必ず抑えておきましょう。
from collections import Counter
n = int(input())
s = [input() for _ in range(n)]
cnt = Counter(s).most_common()
print(cnt[0][0])
ABC230-B - Triple Metre
この問題は、ぱっと見すごく悩んでしまいますよね。しかし、競プロは迷ったときにまず考えるべきことは全探索です!!
部分文字列かを判断するためには単純に oxx を $10^5$ 個繋げた際に s が入っているかどうかを考えれば良いですね。
部分文字列が入っているかどうかの判定は if文の in を使えば良いですね。
サンプルコードは下記のようになります。
s = input()
if s in "oxx" * 10 ** 5:
print("Yes")
else:
print("No")
ABC229-B - Hard Calculation
続いては桁上がりに関する問題ですね。
桁上がりは 2 数を足して 10 以上になれば起こります。
なので、2 数を逆から見ていき、 10 以上になれば No を出力してコードを終了させます。
このような際には、 zip を使用します。
zip は二つのものを同時に見ていくことができ、長さが違う場合には短い方の長さ分だけループします。
桁上がりの判断は2つないとまず不可能なので、今回には最適なものとなっています。
サンプルコードは以下のようになります。
a, b = input().split()
a = list(a[::-1])
b = list(b[::-1])
for i, j in zip(a, b):
if int(i) + int(j) >= 10:
print("Hard")
exit()
print("Easy")
ABC228-B - Takahashi's Secret
続いての4問目は個人的にはこの B 問題 5 つのうち最難関だと思う問題です。
これは、 flag と呼ばれる OK か NGか、プログラミングだと True か False かの2択の bool型の配列を使用すると便利です。
まず、与えられる入力 x は友達なので flag[x - 1] = True とします。
そして、0-indexedで考えて、 x - 1 番目の人と友達である人を順に辿って行きます。
見ていく先が False である場合は、そこは初めて友達であることが判明しているので問題ありませんが、すでに True となっている場合には無限ループをしてしまいますので break しましょう。
少し実装が大変ですが、重要な単元ですのでしっかりと学習しましょう。
n, x = map(int, input().split())
a = list(map(int, input().split()))
# 友達であるかを判断する配列
flag = [False] * n
# Xは友達
flag[x - 1] = True
while True:
if not flag[a[x - 1] - 1]:
flag[a[x - 1] - 1] = True
x = a[x - 1]
else:
break
print(flag.count(1))
ABC227-B - KEYENCE building
こちらは数学問題ですね。
1つずつその面積が存在するかを試してしまうと、最悪で$20 * 1000 * 1000$となってしまい、 Python だとすyこし怖いです。
なので計算量を減らしてみましょう。
$4ab \leqq 4ab + 3a + 3b \leqq 1000$
$4b \leqq 4ab \leqq 1000$
$b \leqq 250$
同様に $a\leqq 250$ までで良いことがわかります(対称性より)。
したがって、計算量が定数倍落ちた上で余裕を持って判定ができるようになりました。
サンプルコードは以下のようになります。
def area(a: int, b: int) -> int:
return 4 * a * b + 3 * a + 3 * b
n = int(input())
s = list(map(int, input().split()))
ans = 0
for i in s:
bool = False
for a in range(1, 251):
for b in range(1, 251):
if area(a, b) == i:
bool = True
if bool:
ans += 1
print(n - ans)
5-4. ABC-C 解説
ここからはいよいよC問題の解説です。
ABC-C は、初心者の壁とよく言われており実際に難しい問題が多いです。
ここをすらすらと解くことができれば初心者は脱出と言えます!!
頑張って解いていきましょう。
ABC231-C - Counting 2
1 問目はこちらの問題です。
問題文がとてもシンプルで読みやすいですね。
クエリが Q 個与えられ、各クエリに対して身長が $x_j$ 以上の生徒は何人かを答える問題です。
毎回 N 人全てに対して答えを探索していると計算量が O(NQ) になり、 TLE となってしまいます。
そこで各クエリに対して高速に答える必要があります。
ここで登場するのが二分探索です。
配列 A をあらかじめソートしておく事により、 Python の bisect が使用できます。
bisect を用いて k がソートされた配列 A に対して何番目に来るのかわかります。
これは計算量が O(logN) なため、とても高速に動きます。
したがって、この問題は各クエリに対して O(logN) なため、O(NlogN) で十分高速に解くことができます。
サンプルコードは以下のようになります。
from bisect import bisect_left
n, q = map(int, input().split())
a = sorted(list(map(int, input().split())))
for _ in range(q):
t = bisect_left(a, int(input()))
print(n - t)
ABC230-C - X drawing
この問題はとにかく問題文がややこしいです。
私自身理解するだけで30分弱かかってしまいました。(これは少し盛っています...)
このような問題文がややこしい際に行うべきことはとりあえず実験をしてみるということです。
なので今回は試しに入力例1について考えてみましょう。
【入力例】
$5 \quad 3 \quad 2$
$1 \quad 5 \quad 1 \quad 5$
【出力例】
$...\#.$
$\#.\#..$
$.\#...$
$\#.\#..$
$...\#.$
ん?たまたまかはわかりませんが、塗られてる部分がX型になってますね。何か性質があるのでしょうか?
なぜこの出力が出来上がるのかをまずは考えてみましょう。
黒く塗る条件は2つあります。
-
$max(1 - A, 1 - B) \leqq k \leqq min(N - A, N - B)$をみたす全ての整数 $k$ について $(A + k, B + k)$ を黒く塗る。
-
$max(1 - A, B - N) \leqq k \leqq min(N - A, B - 1)$をみたす全ての整数 $k$ について $(A + k, B - k)$ を黒く塗る。
しっかりと条件を眺めると、見えてくることがあります。
ある値 k が1つ目の条件の満たしているとき、その k の座標対して、 $(A, B)$だけ平行移動した点が黒く塗られることがわかります。
例えば条件1について、 $1 \leqq k \leqq 5$ が満たしており、 $A = 3, B = 6$ だとします。
このとき塗られる点は、$(4, 7), (5, 8), (6, 9), (7, 10), (8, 11), (9, 12)$の6つです。
これは実際にプロットしてみればわかりますが、右斜め下に塗られて行きます。
そして条件2についても同じようにやってみると、これは左斜め下に塗られていくことがわかります。
なので答えは X のような図形の部分的な場所を出力すれば良いです。
黒く塗る部分について、$(A, B)$だけ平行移動してることに気をつけましょう。
n, a, b = map(int, input().split())
p, q, r, s = map(int, input().split())
# 初期状態は全て . にする
ans = [["."] * (s - r + 1) for _ in range(q - p + 1)]
# 1つ目の条件について探索する
for i in range(p, q + 1):
for j in range(r, s + 1):
dx = i - a # x座標の増加量
dy = j - b # y座標の増加量
if dx == dy: # x座標の増加量 = y座標の増加量 の場合に条件を満たす
if max(1 - a, 1 - b) <= dx <= min(n - a, n - b):
ans[i - p][j - r] = "#" # -p, -r は (p, r)スタートのために並行移動する
# 2つ目の条件について探索する
for i in range(p, q + 1):
for j in range(r, s + 1):
dx = i - a # x座標の増加量
dy = j - b # y座標の増加量
if dx == -dy: # x座標の増加量 = -y座標の増加量 の場合に条件を満たす
if max(1 - a, b - n) <= dx <= min(n - a, b - 1):
ans[i - p][j - r] = "#" # -p, -r は (p, r)スタートのために並行移動する
for i in ans:
print(*i, sep="")
ABC229-C - Cheese
続いての問題は載せられるチーズの最大量の問題です。
この問題はちょっと読解が難しいですね。
問題の優しいポイントは、与えられる入力が全て $1[g]$ あたりの美味しさであるということです。
なので、単純に美味しさが高いものからソートしていって大きいものから $W[g]$ とっていけば良いことがわかります。
これは貪欲法と呼ばれるアルゴリズムの1つで、その場その場で最善のものを選択すると必然的にそれが解になるというものです。
貪欲法は全てのアルゴリズムを考える上での基礎だと思っているので常に発想としては思い浮かべるようにしましょう。
n, w = map(int, input().split())
a = [list(map(int, input().split())) for _ in range(n)]
# 全て1[g]あたりの美味しさは同じなので美味しさが大きい順にソートする
a.sort(reverse=True, key=lambda x: x[0])
now = 0 # 既に乗せたチーズの量
ans = 0
for i in range(n):
if now >= w: break
if now + a[i][1] <= w: # これから乗せるチーズを考慮しても w[g] を超えない場合
now += a[i][1]
ans += a[i][0] * a[i][1]
else: # 超えてしまう場合は超えないようにピッタリ食べる
ans += a[i][0] * (w - now)
break
print(ans)
ABC228-C - Final Day
この問題は4日目で自分だけが最高得点である300点、自分以外の全員が0点を取った際の場合が自分の順位が一番上がる状況です。
なので、あらかじめ、3日間の合計点数に基づく順位表を作成し、その k 位の人の点数を抑えておきます。
そして N 人に対してそれぞれ300点を加算した際に k 位の人の点数よりも高ければ Yes そうでなければ答えは No となります。
このようにあらかじめ前処理をしておくことで問題の見通しが良くなることはとても良くあるので抑えておきましょう!
n, k = map(int, input().split())
p = [list(map(int, input().split())) for _ in range(n)]
# N人の3日間の合計を降順に格納する配列
a = sorted([sum(p[i]) for i in range(n)], reverse=True)
for i in range(n):
# i番目の人が300点を取って、K番目の人よりも高い場合
if sum(p[i]) + 300 >= a[k - 1]:
print("Yes")
else:
print("No")
ABC227-C - ABC conjecture
問題解説の最後は数学問題です!!
なぜ直近5回まで解説したかというと、ここまでガッツリとした数学問題が出題されていなかったからです。
最初の方でもお話ししたように、AtCoder では数学問題がよく出題されます。ですのでこのような問題になれるようにして行きましょう!
問題文はシンプルです。
入力 N に対して、$A \leqq B \leqq C$ かつ $ABC \leqq N$ であるような正の整数の組 $(A,B,C)$ の個数を求めるという問題です。
数学問題で特に重要なのが制約です。
制約の大きさによってどこまで計算量を減らす必要があるのか変わってきます。
今回の場合は $1 \leqq N \leqq 10^{11}$なので O(N) などの解法では TLE してしまいます。
そこで思いつくのが O($\sqrt{N}$)などですが、今回は文字が3つ動くので少し難しそうです。
ここで大事なのは不等式から範囲を絞るということです。
$A^3 \leqq ABC \leqq N$
$A^3 \leqq N$
$A \leqq N^{\frac{1}{3}}$
とわかるので、探索する A の範囲は $N^{\frac{1}{3}}$ までで良いことがわかります。
次に B の範囲を絞っていきます。
$BC \leqq \frac{N}{A}$
$B×B \leqq BC \leqq \frac{N}{A}$
$B^2 \leqq \frac{N}{A}$
$B \leqq \sqrt{\frac{N}{A}}$
したがって、探索する B の範囲は $\sqrt{\frac{N}{A}}$までで良いことがわかります。
ここまで、範囲が絞れたらあとは条件を満たす$ C \leqq \sqrt{\frac{N}{AB}}$を満たす C の個数を求めれば良いです!
サンプルコードは以下のようになります。
n = int(input())
ans = 0
for a in range(1, int(n ** (1 / 3)) + 10):
for b in range(a, int((n / a) ** 0.5) + 10):
ans += max(0, int(n // (a * b)) - b + 1)
print(ans)
また、こちらの問題については、以下の記事で私が以前に詳しく解説しているので気になる方は見てみて下さい。
6. 初心者にオススメの勉強サイト
僕自身も Twitter をしていると、最近はよく DM で競技プログラミングを始めたばかりの方から、「何を最初に行えば良いですか?」, 「どうやって勉強されてきましたか?」などと言った質問をよくいただきます。
なので今章では、競技プログラミングを始めたばかりの方にオススメの勉強方法について紹介したいと思います。
6-1. AtCoder Problems
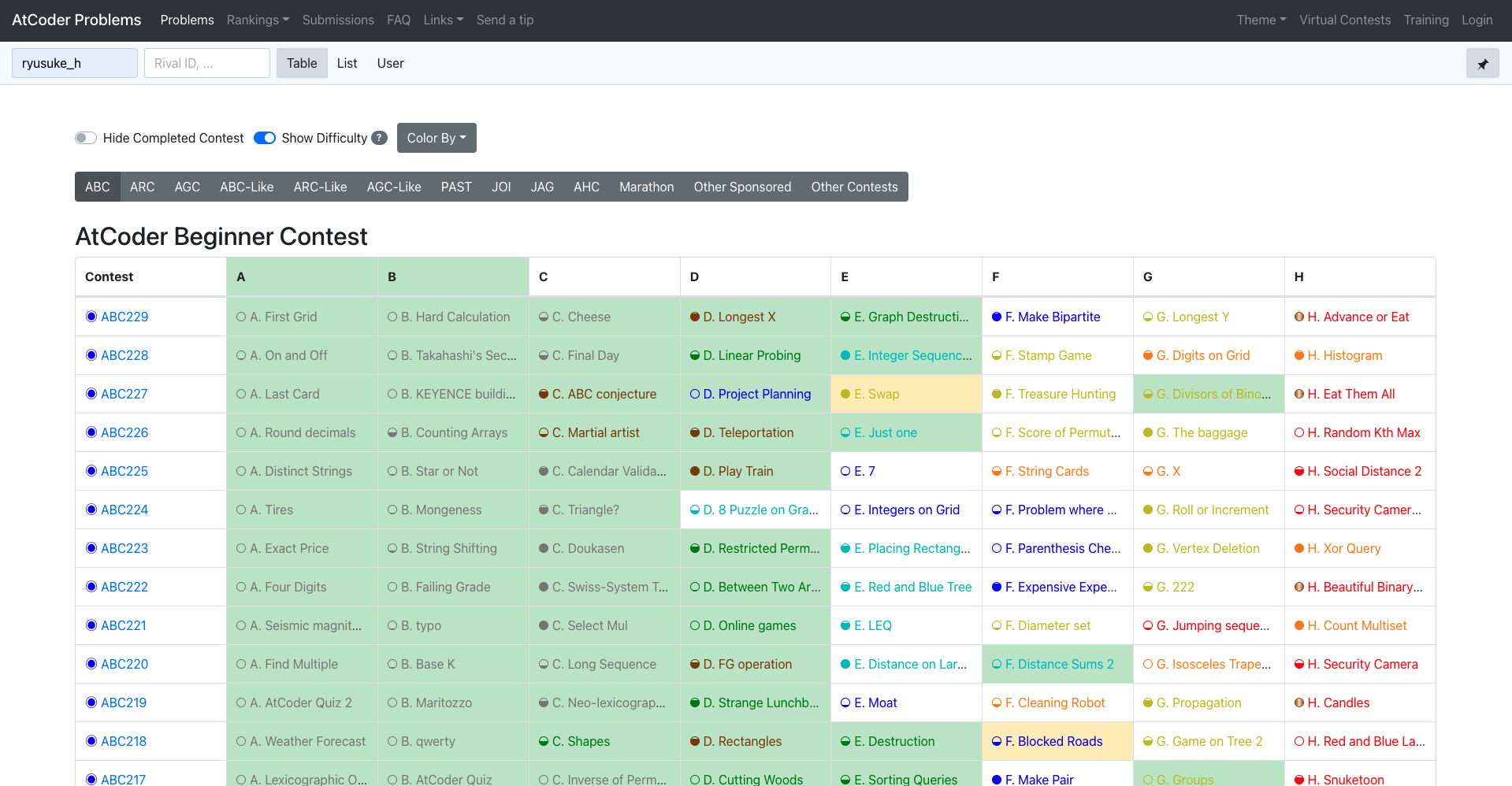
一番のオススメは AtCoderProblems です。
ある程度競技プログラミングを行なっている方ならほぼ全員が使用していると思われるツールです。
ここでは過去のコンテストで出題された問題を解き直したり、 JOI(Japanese Olympiad in Informatics) で出題された問題などを解くことができます。やはり過去問を解くことは何よりも大事なことなので必ず使用することをオススメします。
まず、左上の User ID に AtCoder の ID を入れると、自分がどの問題を解いているのか、確認することができます。
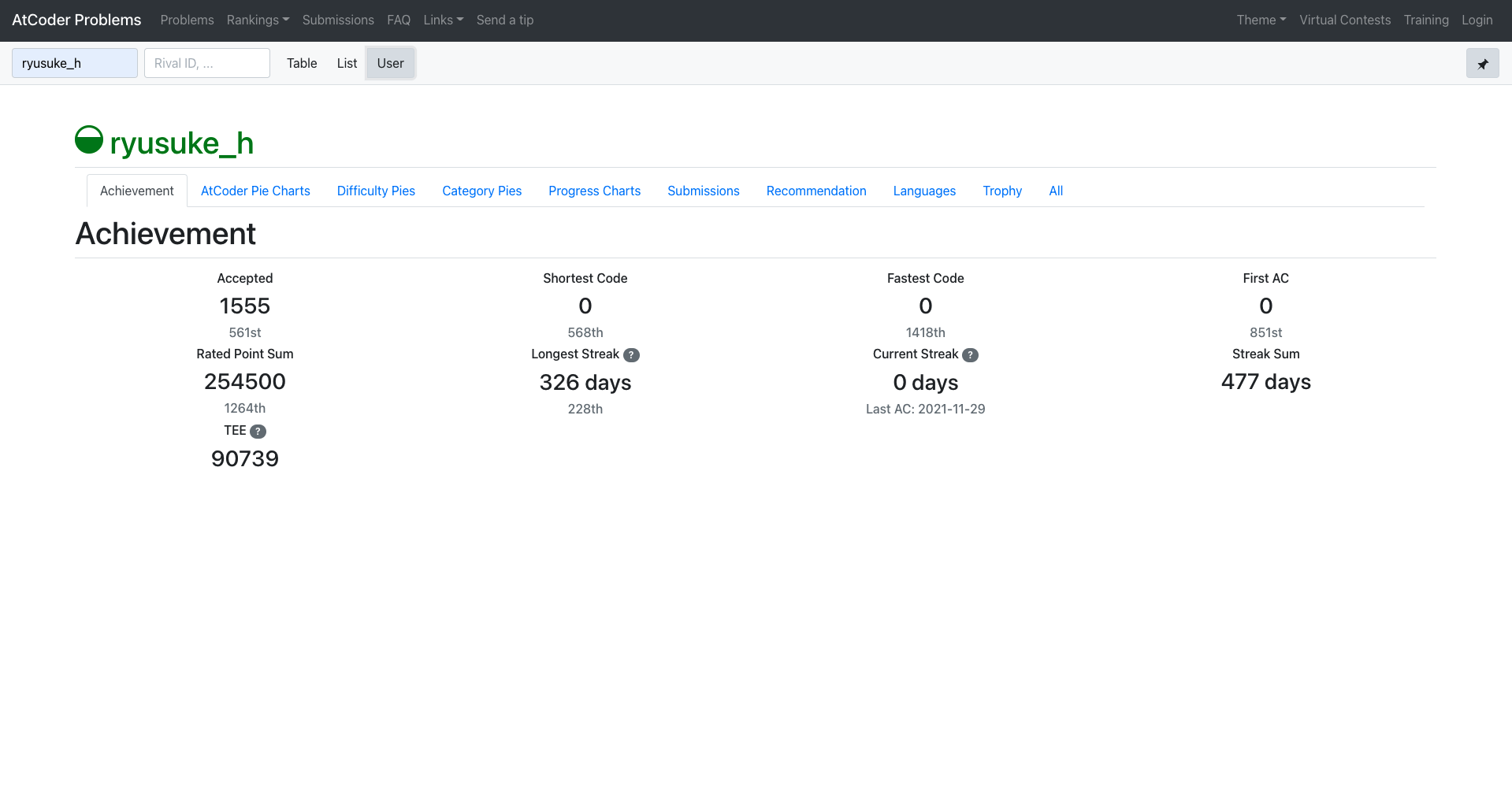
User の所をクリックすると、自分の功績を見ることができます。
これを見るだけで、ユーザーランキングや何問解いてきたのか確認できるため、モチベーションの維持にも繋がります。
僕も普段精進をしているときは必ず開いています。ぜひ使用してみて下さい。
6-2. アルゴ式
続いては アルゴ式 です。
アルゴ式は最近公開されたサイトで、現在は Beta版となっています。プログラミングよりも最初の段階である算数のレベルの問題から始まり、プログラミングの文法が学べるのはもちろん、応用的な問題も公開されているのでとても勉強になります。
また、解説が C++, Python で書かれているため、この2つを勉強している方には特にオススメのサイトとなっています。
さらに、毎日問題が更新されているため、解いていて飽きることがありません。
まずはログインしてみましょう。
6-3. 競プロ典型90問
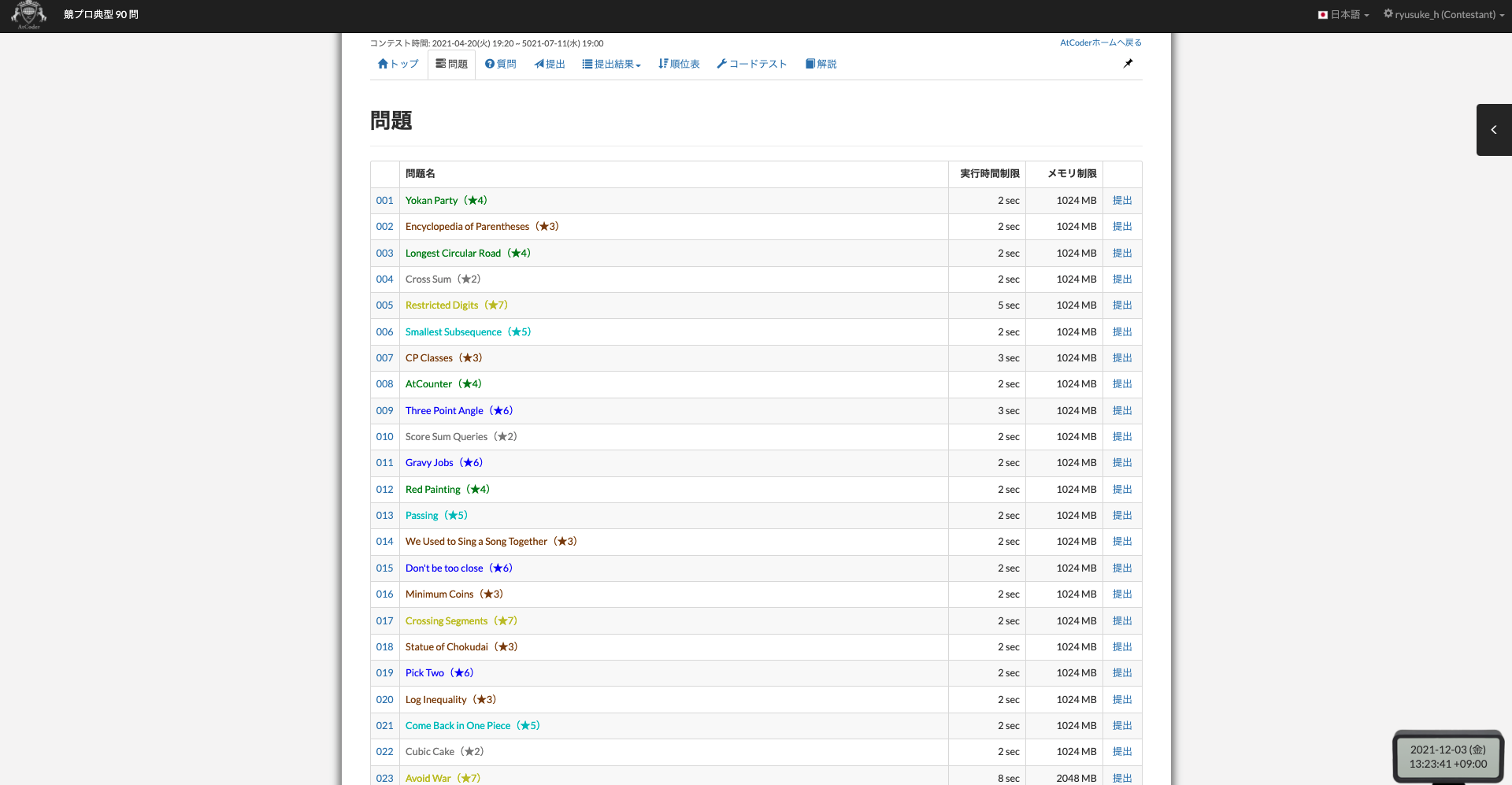
続いては 競プロ典型90問 です。
こちらは @e869120 さんが作成したものであり、競技プログラミングでよく出題されるアルゴリズムや数学の問題などを90問にピックアップして作られたコンテンツとなっています。
難易度が ☆2 〜 ☆7 まであり、簡単なアルゴリズムの問題からとても難しいレベルの問題までが厳選されてあるのでコスパは最大級だと思います。
なお、1, 2, ... 89, 90 と番号順に解いていくと、簡単な問題と難しい問題がバラバラに出題されているので、難易度の低いものから解いていくのがオススメです。
なお、競プロ典型90問の Python による解答を僕の GitHub に上げているので、 Python を使われている方は良ければ参考にしてみて下さい。
6-4. レッドコーダーが教える、競プロ・AtCoder上達のガイドライン【中級編:目指せ水色コーダー!】
最後は 分野別 初中級者が解くべき過去問精選 100 問 です。
ここ最近で競技プログラミングを始められた方に関してはこの "分野別 初中級者が解くべき過去問精選 100 問" (以下、省略して精選 100 問) を知らない方も多いのではないでしょうか?
こちらは [#6-3. 競プロ典型90問](#6-3. 競プロ典型90問) と同じ @e869120 さんが作成した問題100問です。
典型90問よりも、基礎的で必ず必要になるアルゴリズムを分野別で紹介されているので、勉強したいアルゴリズムの理解を一気に深めることができます。
解くと必ず力の付く問題ばかりですのでかなりオススメです!!
7. AtCoder を行う上でおすすめのWebツール
普段精進をする際でも便利で役に立つWebツールというものはたくさんあります。
中でも個人的にお気に入りのものを紹介したいと思います。
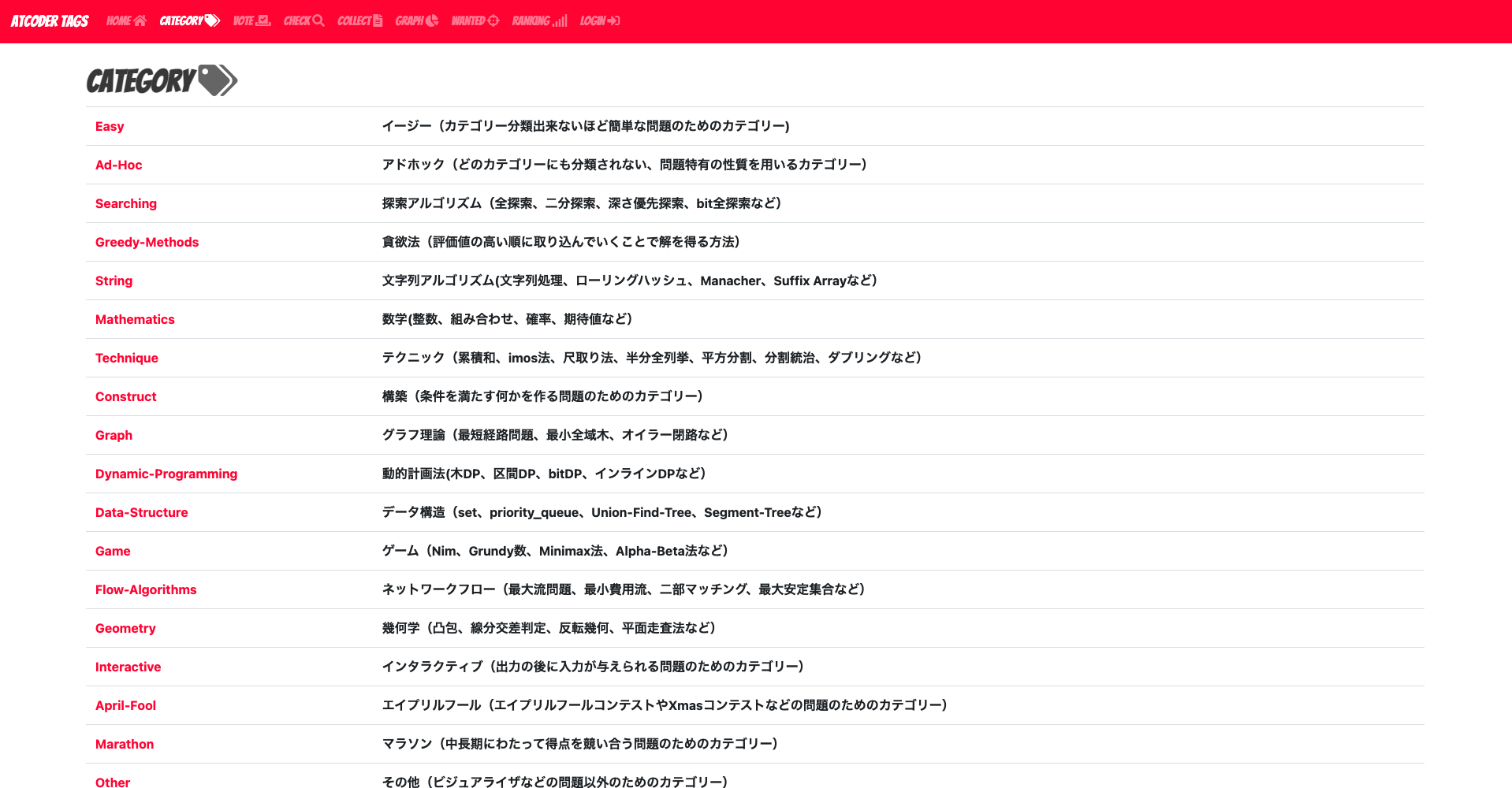
7-1. AtCoder Tags
最初にオススメするWebツールは AtCoder Tagsです。
特にこのサイト内にあるカテゴリ欄は特定のアルゴリズムを勉強したい際などにとても参考になるサイトです。
あるアルゴリズムを勉強した後に、「もう少し類題を解きたい!」などとなった際に、このカテゴリから検索をすると類題が大量に出てきます。
さらに知識をつけたい、理解を深めたいなどと思った際にはぜひ使用してみてください。
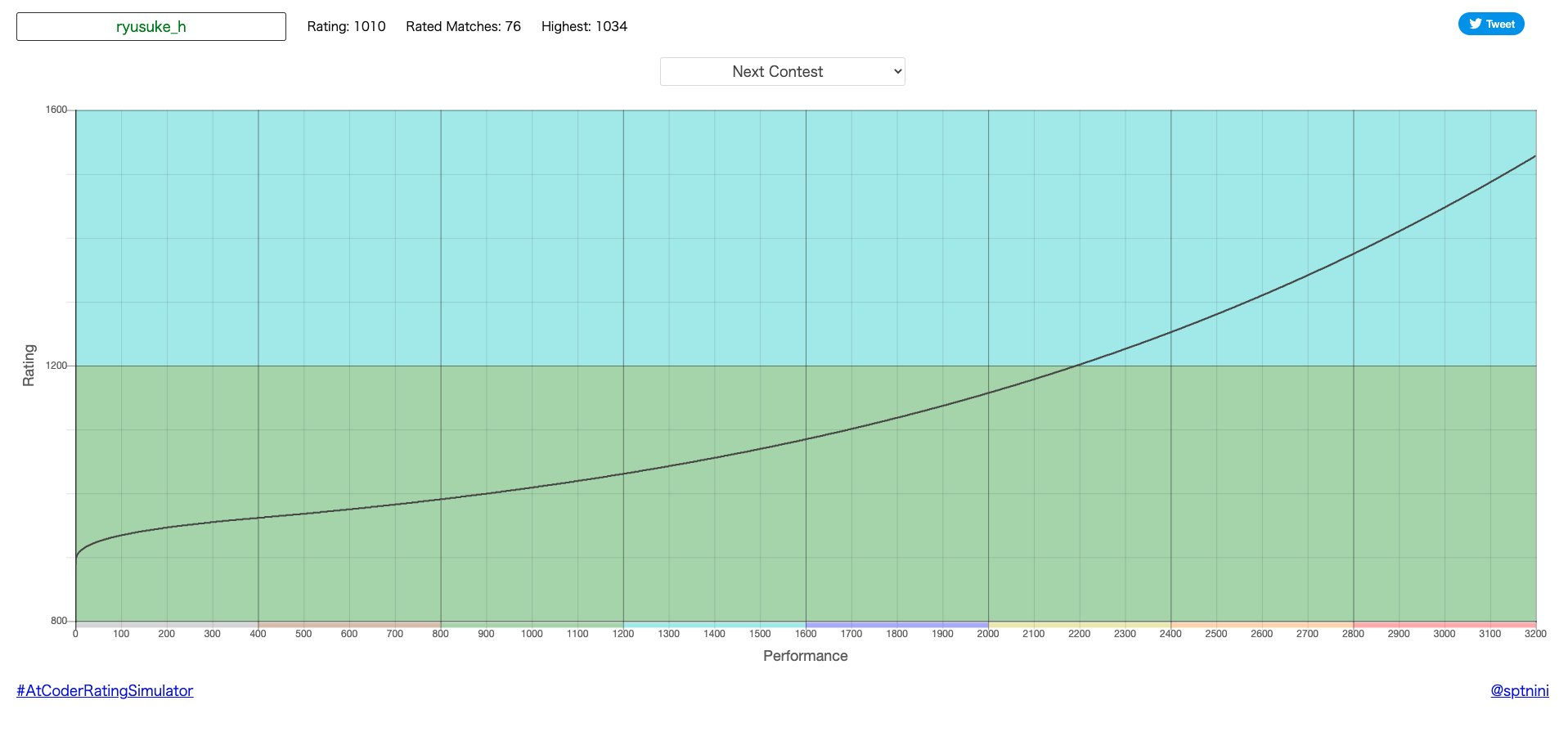
7-2. AtCoder Rating Simulator
AtCoder Rating Simulator は、自分が〇回どれほどのパフォーマンスを取ると、どれくらいのレートに行けるのかが一目でわかります!
目指しているレートや色がある方にとってはモチベーションの維持につながります!!!
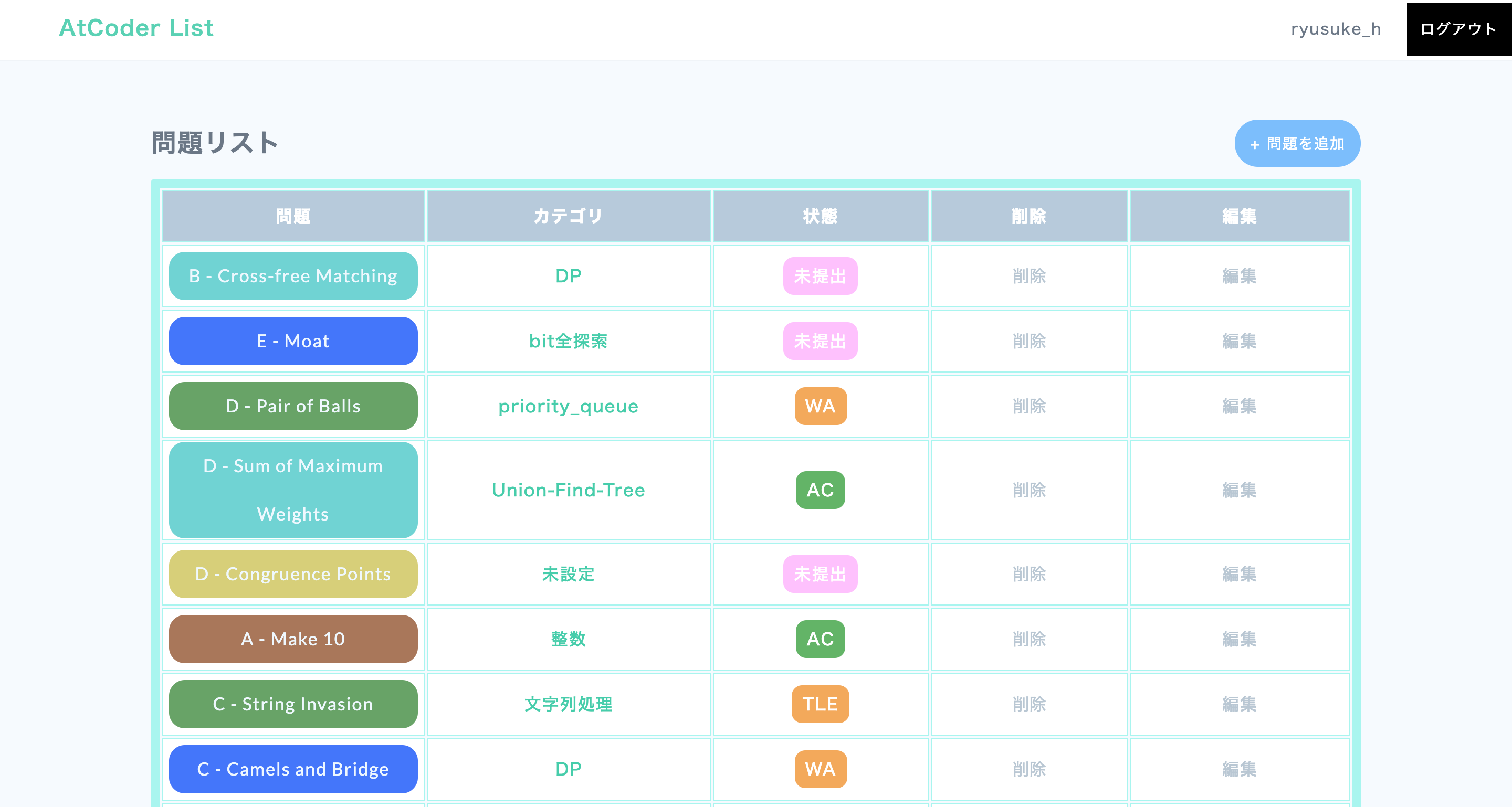
7-3. AtCoder List
最後は AtCoder List です。
これは2ヶ月ほど前に私が作成したWebアプリです。
競技プログラミングをしていると、「解きたい問題が増えすぎる」、「解きたいけど時間がない!」、などと言った場面がたくさんあります。
そのような際に自分で問題を保管して溜めておけるのがこの AtCoder List です。
自分で作って言うのもアレですが、とても見やすくできたと思います。
ぜひ使ってみて下さい!!
ソースコードも GitHub にて公開しています。
8. 便利な拡張機能
競技プログラミングは正確さや実装能力も当然要求されますが、解くまでのスピードというのもとても大事な要素の1つです。
そこで、AtCoder のコンテスト中に入れておくと良い拡張機能について紹介します。
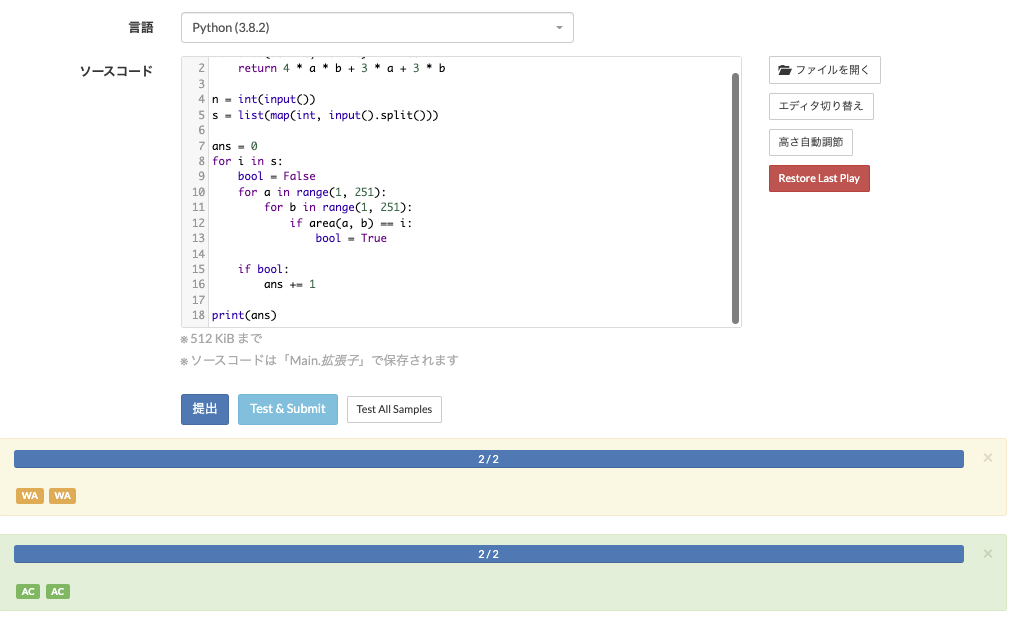
8-1. AtCoder Easy Test
一番初めに紹介する拡張機能は AtCoder Easy Test です。
問題を解いている最中に入力例を何度もコピーして出力が合っているかどうかを判断するのはとても大変です...
そんなときに大活躍するのがこちらの拡張機能です。
ボタンひとつでペーストしたコードに対して入力例に対する出力が合っているかどうかを判断してくれます。
これだけで AC するまでの時間が大きく変わります!!
必ず入れておくことをオススメします。
8-2. AtCoderPerformanceColorizer
次に紹介するのが AtCoderPerformanceColorizer です。
自分のレートの推移を色付きで見ることができます。
なくても問題は何もないのですが、モチベーションややる気の維持につながります。
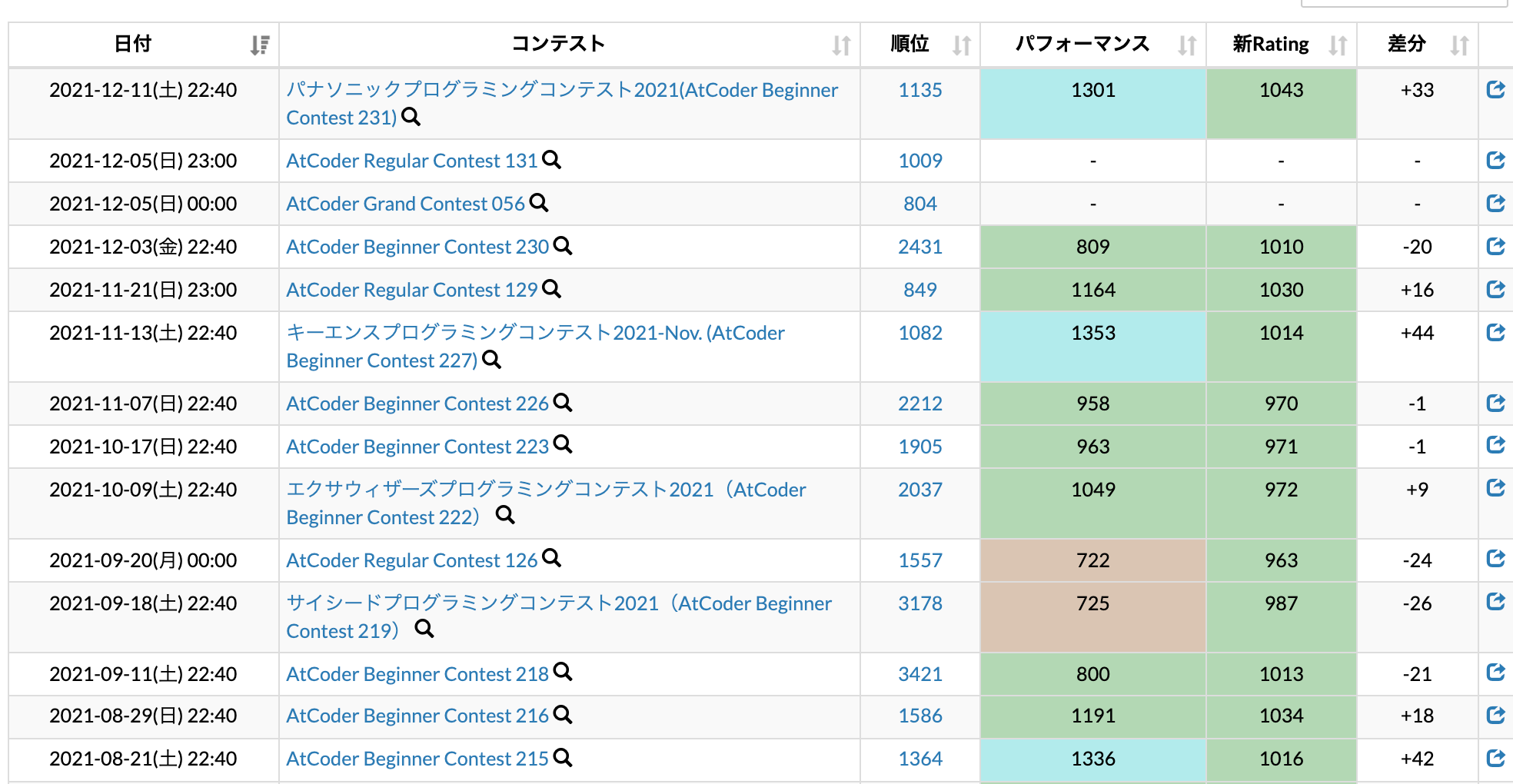
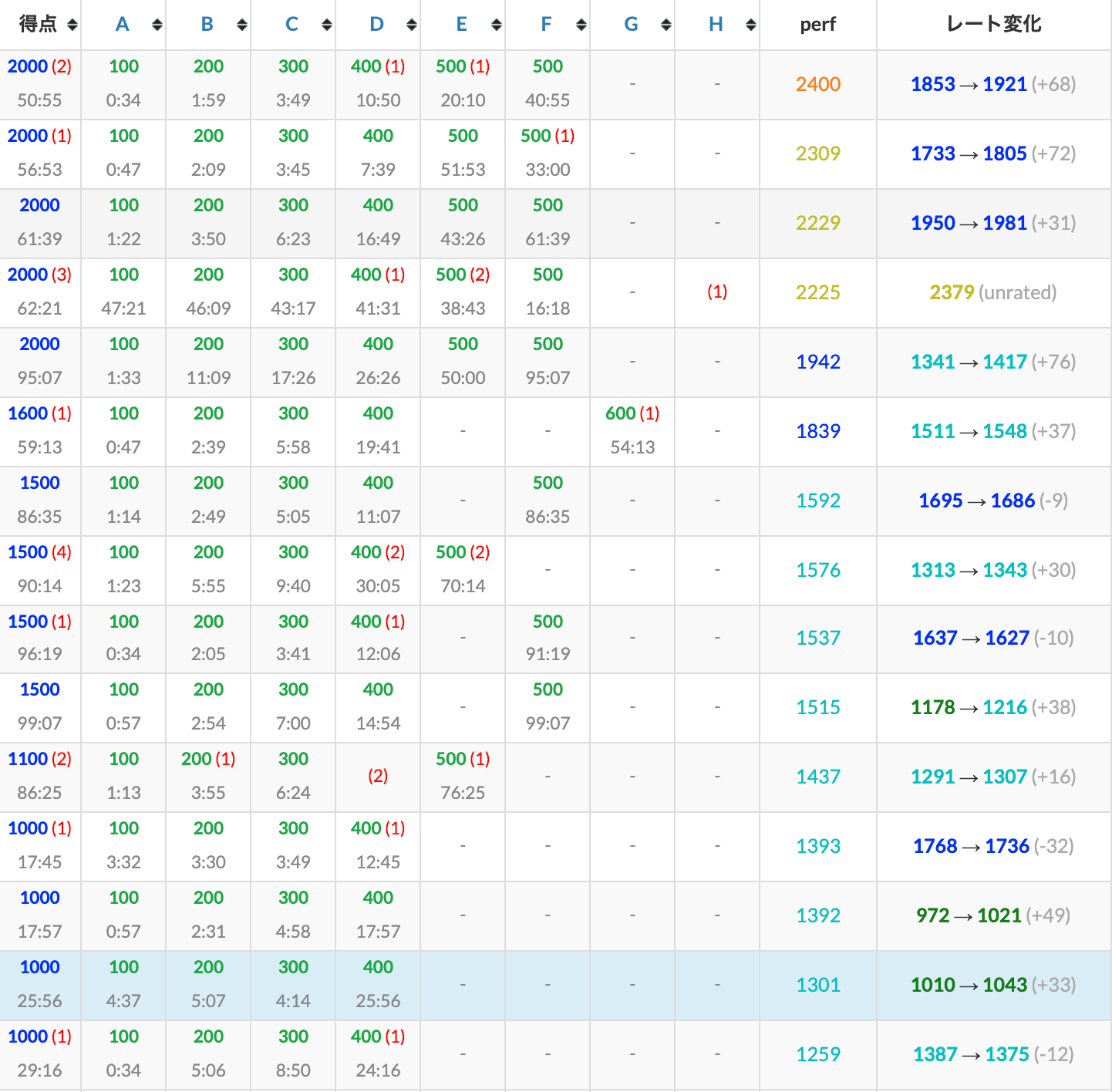
【AtCoderPerformanceColorizer 導入前の成績】
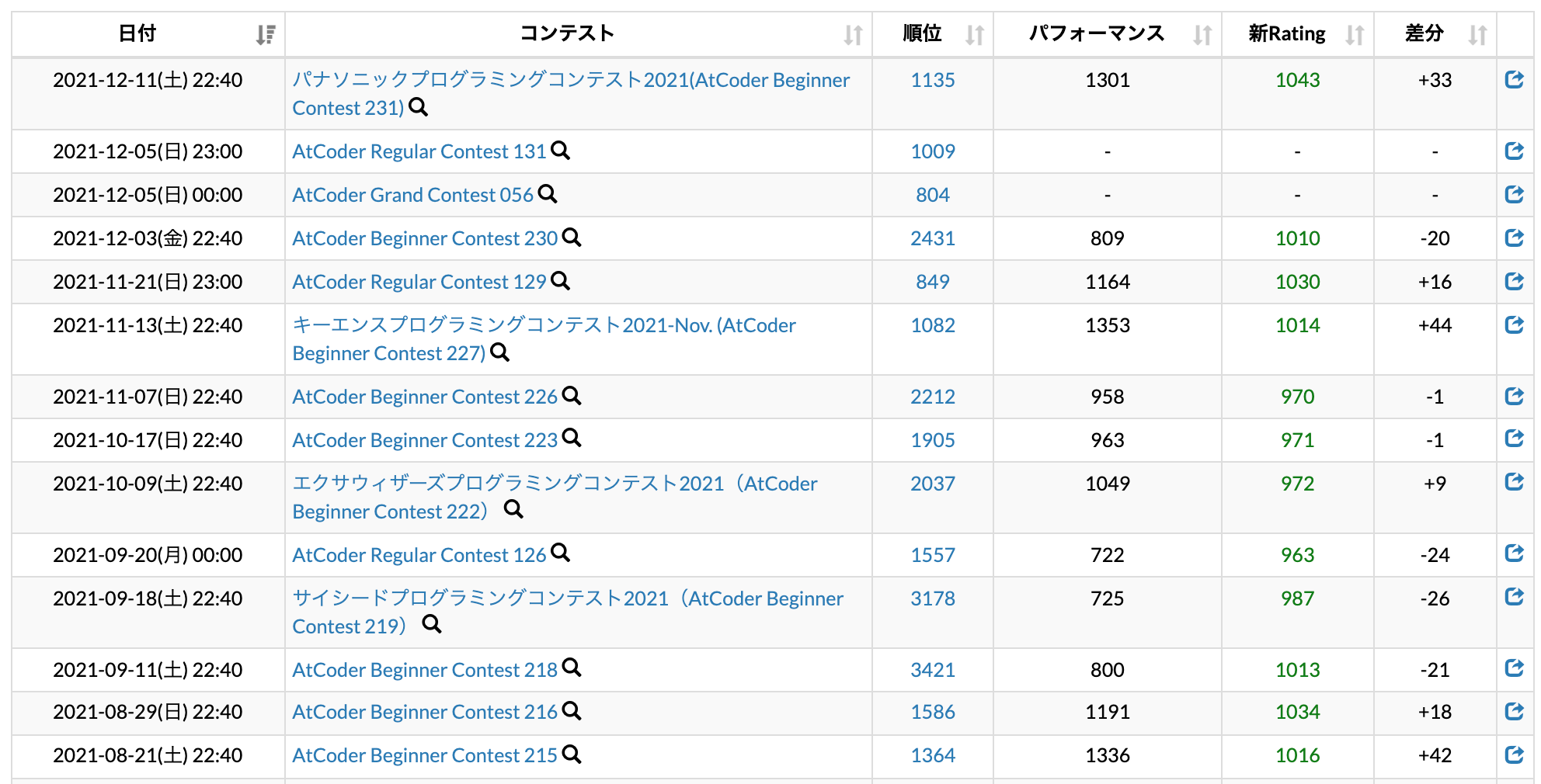
【AtCoderPerformanceColorizer 導入後の成績】
8-3. ac-predictor
3つ目は、 ac-predictor です。
これはコンテスト中に自分が今どの立ち位置にいて、このままコンテストが終了すると、何位くらいになり、パフォーマンスはどれくらい出るのか可視化してくれます。
「最後の結果発表まで待ちきれない!」という方はぜひ入れてみることをオススメします。
9. ライブラリを自分で作成する
あるアルゴリズムを完璧に理解しても、それを毎回書いていると時間がかかってしまう、と言うケースがよくあります。
ググればすぐに出てくるものもありますが、人のコードほど信用できないものはないので最初はなんでも自分で作ってみることをオススメします。
そしてそれを保存しておくと、次回以降使いまわすことができます。
いくつか例を載せておきます。
AtCoder を始めたばかりの方はなんのことかわからないと思うのでここは飛ばしていただいて問題ないです。
9-1. Union-Find
初めて学習するアルゴリズムが Union-Find という方はよく聞きます。
class UnionFind:
def __init__(self, n):
self.n = n
self.p = [-1] * n
def leader(self, a):
while self.p[a] >= 0:
a = self.p[a]
return a
def merge(self, a, b):
x = self.leader(a)
y = self.leader(b)
if x == y: return x
if self.p[x] > self.p[y]:
x, y = y, x
self.p[x] += self.p[y]
self.p[y] = x
return x
def same(self, a, b): return self.leader(a) == self.leader(b)
def size(self, a): return -self.p[self.leader(a)]
9-2. ワーシャルフロイド法
主に緑を超えてくると要求されやすくなってくるアルゴリズムです。
def warshall_floyd(d):
for k in range(n):
for i in range(n):
for j in range(n):
d[i][j] = min(d[i][j], d[i][k] + d[k][j])
return d
INF = 10 ** 20
n, m = map(int,input().split()) # 頂点数・辺の数
d = [[INF] * n for _ in range(n)] # 隣接行列の初期化
# 自分自身へのコストは0
for i in range(n):
d[i][i] = 0
# 与えられた距離の初期化
for i in range(m):
x, y, r = map(int,input().split())
d[x - 1][y - 1] = r
d[y - 1][x - 1] = r
# sからtへの最短距離を求める
dist = warshall_floyd(d)
9-3. トポロジカルソート
要求レベルは高いわけではないのですが、自分はつい最近まで知らなかったのでライブラリ化しました。
from collections import defaultdict
from heapq import heappop, heappush
n, m = map(int,input().split())
g = [[] for _ in range(n)]
d = defaultdict(int) # d[i] := 頂点iに入ってくる辺の個数
for _ in range(m):
a, b = map(int,input().split())
g[a - 1].append(b - 1)
d[b - 1] += 1
q = []
# スタート地点を決める
for i in range(n):
if d[i] == 0:
heappush(q, i)
ans = []
l = 0 # 答えの長さ
while l < n:
if len(q) == 0:
exit(print(-1))
v = heappop(q)
ans.append(v + 1)
l += 1
for i in g[v]:
d[i] -= 1
if d[i] == 0:
heappush(q, i)
print(*ans)
これ以外にも数十個ライブラリを自分は保存しています。
下記リンクにまとまっているのでよければ参考にしてみてください。
10. 最後に
まずはじめにここまで記事を読んでくださりありがとうございました。
Qiita に投稿すること自体が初めてだったので少し緊張しながら書いてましたが、なんとかアドカレの期日には間に合ってよかったです。
AtCoder を始めたばかりの頃は自分自身もよくわからなくて途方に暮れていた時期があったので1人でも多くの方に役に立てばと思います。
伝えたいことはほぼ全て伝えきれたと思います!
最後まで読んでくださりありがとうございました!