はじめに
明治大学 総合数理学部Advent Calender 2017の9日目の記事。僕の担当は9日目にして4回目。今日で一応Network関連の連載は終わり。(次から何やるか考えないと、、、)
目標
Network上の反応拡散方程式を定義して、その性質を見る。
前提知識
- 線形代数
- 微積分
- 微分方程式
- 力学系の基礎
- Scale Free Network(12/1の僕の記事)
- Network上のLaplacian(12/3の僕の記事)
- Network上の拡散方程式(12/6の僕の記事)
「普通の」反応拡散方程式
ざっくりとしか紹介しないが、所謂「普通の」反応拡散方程式とは、拡散現象と反応(化学反応とか捕食・被食関係とか)が普通の空間で行われている現象についてを表すモデル。2変数のモデルであれば適当な初期条件と境界条件の元で次の通りの式にて一般的に表される。
\begin{align}
\begin{cases}
\dfrac{\partial u}{\partial t} = f(u, v) + D_u\Delta u\\
\dfrac{\partial v}{\partial t} = g(u, v) + D_v\Delta v
\end{cases}
\end{align}
$D_u$と$D_v$はそれぞれ$u$と$v$に関する拡散係数で、$f$と$g$は反応を表す項である。式を眺めても、もちろん面白いかもしれないが、それ以上にもっと面白いのはこれのSimulationである。例えば、解糖系(詳しくは紹介しない)を表すGray-Scottモデルという反応拡散系を空間2次元でSimulationすると、下のような模様が出る。

反応拡散系とはこういう面白いパターンが出るもの、という認識で概ね間違いない。もっと気になったら「動物 模様 反応拡散」とかでググったら、きっともっと面白いパターンが見れると思う。
Network上の反応拡散方程式の定義
それでは、Network上でも反応拡散方程式がどう定義できるか見ていこう。これは前回のNetwork上の拡散方程式についてわかっていれば、簡単な話である。次の2つの事柄を考えれば良い。
- Node上に2種類の「何か」$X$と$Y$があって、Edgeを介して隣のNodeに拡散する。
- Node上でそれら2種類が何らかのルールに従って反応する。
1番についてはそのまま前回の話。2番はNetworkで共通のルールがあったときにそれらの反応を微分方程式に起こせるので、上で紹介した「普通の」反応拡散方程式の出てきた$f(X, Y)$と$g(X, Y)$を使えば良いだけ。
そうすると、次の感じのNetwork上の2変数反応拡散方程式が定義できる。$$\frac{d\boldsymbol{X}}{dt} = \boldsymbol{F}(\boldsymbol{X}, \boldsymbol{Y}) + D_X L\boldsymbol{X}$$ $$\frac{d\boldsymbol{Y}}{dt} = \boldsymbol{G}(\boldsymbol{X}, \boldsymbol{Y}) + D_Y L\boldsymbol{Y}$$ここで、$L$はLaplacian行列、$D_X$と$D_Y$はそれぞれの拡散係数、$$\boldsymbol{X} = (X_1, \cdots, X_N)^T$$ $$\boldsymbol{Y} = (Y_1, \cdots, Y_N)^T$$ $$\boldsymbol{F}(\boldsymbol{X}, \boldsymbol{Y}) = (f(X_1, Y_1), \cdots, f(X_N, Y_N))^T$$ $$\boldsymbol{G}(\boldsymbol{X}, \boldsymbol{Y}) = (g(X_1, Y_1), \cdots, g(X_N, Y_N))^T$$である。
$X$と$Y$がそれぞれ独立して拡散しているのと、Network共通のルール($f$と$g$により表現される)で各Nodeの上で他のNodeとは独立して反応が起きていることが表せている。
Network上の反応拡散方程式の性質
本節はガッツリ数学です。アレルギーをお持ちの方は飛ばすことをおすすめします。
一様解
Network上の反応拡散方程式には特殊な解、一様解があることを紹介する。端的にいうと、全てのNodeにおいて同じ値を取る解のことである。直感的には、Laplacian行列には拡散の効果、すなわち周りとの一様化をはかる効果があるので、既に一様になった状態ならば、拡散の影響は見た目には無いに等しくなる、ということである。ただ、ここでは反応についても考えねばならないので、Network上の反応拡散方程式では、反応項だけを取り出した、次の2変数常微分方程式の解を全Nodeが持っていれば、ちゃんとそれが一様な解となってくれる。つまり、全Nodeが
$$\frac{dX}{dt} = f(X, Y)$$ $$\frac{dY}{dt} = g(X, Y)$$の解$(\bar{X}, \bar{Y})$の値を取れば、それは上のNetwork上の反応拡散方程式の解にもなっているということである。ここで、特に$(\bar{X}, \bar{Y})$が先程の反応だけの2変数常微分方程式の平衡点であるようならば、一様な定常解と呼ぶ。
一様解の安定性
拡散というものは一様化する働きがある、といったが、反応拡散系ではしばしばこの拡散によって、安定なものが不安定になることがある。この不安定化によって、反応拡散系ではパターンを形成することがAlan Turingによって示された。Network上の反応拡散方程式でも同じようにこの不安定化が起きることが示せる。
まずは、一様な定常解を考え、そこにちょっとした揺らぎを加える。この揺らぎが時間とともに増大するようなら、定常解は不安定する。なので、揺らぎを$x(t) = (x_1, \cdots, x_n), y(t) = (y_1, \cdots, y_n)$として、$$X_i(t) = \bar{X} + x_i$$ $$Y_i(t) = \bar{Y} + y_i$$とする。この揺らぎをLaplacian行列の固有ベクトル$\phi^{[1]}, \cdots, \phi^{[N]}$で展開すると、展開係数を$p_\alpha(t), q_\alpha(t)$として、$$x_i(t) = \sum_{\alpha = 1}^Np_\alpha(t) \phi_i^{[\alpha]}, \quad y_i(t) = \sum_{\alpha = 1}^Nq_\alpha(t) \phi_i^{[\alpha]}$$と表せる。この展開係数$p_\alpha(t)$と$q_\alpha(t)$が時間とともに増大するようなら、一様解は不安定化すると言える。
この揺らぎを元の反応拡散方程式に代入して、$(\bar{X}, \bar{Y})$周りで線形化(力学系の話)すると、各$\alpha$について次のような微分方程式を得る。
\frac{d}{dt}
\left(
\begin{matrix}
p_\alpha \\ q_\alpha
\end{matrix}
\right)=
\left(
\begin{matrix}
f_X + D_X \Lambda^{[\alpha]} & f_Y \\
g_X & g_Y + D_Y \Lambda_{[\alpha]}
\end{matrix}
\right)
\left(
\begin{matrix}
p_\alpha \\ q_\alpha
\end{matrix}
\right)
ここで、$f_X, f_Y, g_X, g_Y$は$f(X, Y)$と$g(X, Y)$を$(\bar{X}, \bar{Y})$周りでTaylor展開したときの一次の項の係数であり、$\Lambda^{[\alpha]}$はLaplacian行列の$\alpha$番目に大きい固有値である。
(問: この常微分方程式を導け。)
これは簡単な2変数の線形微分方程式なので、安定性はこの2×2の係数行列の固有値を調べればよいことが分かる。(Hartman-Grobmanの定理(力学系の話)によれば、この係数行列の固有値の実部が全て0でなければ、この行列の固有値を調べることは、線形化する前の状態の安定性を調べることと同値である。)具体的には、この固有値が一つでも実部が正なものがあれば、$p_\alpha(t)$と$q_\alpha(t)$は時間と共に発達する。
実際にこの固有値は$$\lambda_\pm^{[\alpha]} = \frac{1}{2}(f_X + g_Y + (D_X + D_Y))\Lambda^{[\alpha]} \pm \sqrt[]{4f_Yg_X + (f_X - g_Y + (D_X - D_Y)\Lambda^{[\alpha]})^2}$$により与えられる。
(問: この固有値を導け。)
以上より、$\alpha = 1, \cdots, N$の内どれかにおいて、$\lambda_\pm^{[\alpha]}$の実部が正になるようなことがあったら、揺らぎは発達し、一様な定常解は不安定化する。これは実際のLaplacian行列の固有値に影響を受けるところが大きい。
こうして一様な解が不安定化することをTuring不安定性と呼ぶ。
Simulation
実際に$f$と$g$において、次のような三村-Murrayモデルという捕食と被食を表すモデルを使ってNetwork上の反応拡散方程式をSimulationしていこう。$$f(X, Y) = \left(\frac{1}{9}(35 + 16X -X^2) - Y \right)X$$ $$g(X, Y) = -\left(\left(1 + \frac{2}{5} Y\right) - X\right)Y$$
この時、この反応だけを考えた2変数常微分方程式の安定な平衡点は(5, 10)なので、初期状態として、全てのNodeが(5, 10)となるような一様な状態を考える。ここにちょっとした揺らぎを加えることで、パターンができるかどうかを見ていく。
揺らぎの発展を調べるために$D_X = 0.06, D_Y = 1.8$として前節で定義した$\lambda_\pm^{[\alpha]}$の実部をプロットしてみると、下のようになる。横軸を実際のLaplacian行列の固有値、縦軸を$\lambda_\pm^{[\alpha]}$としている。
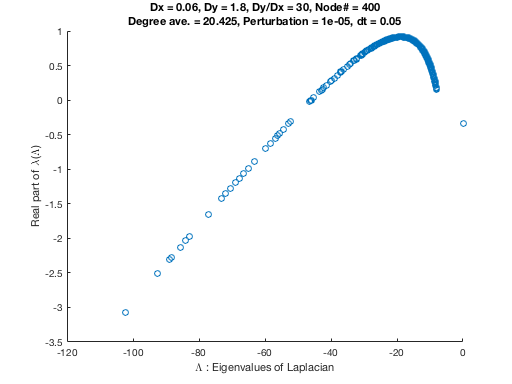
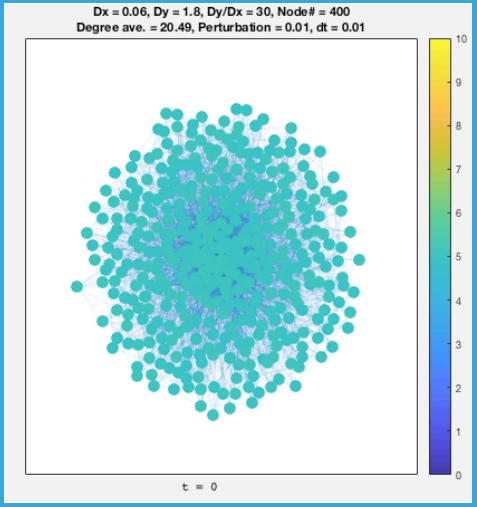
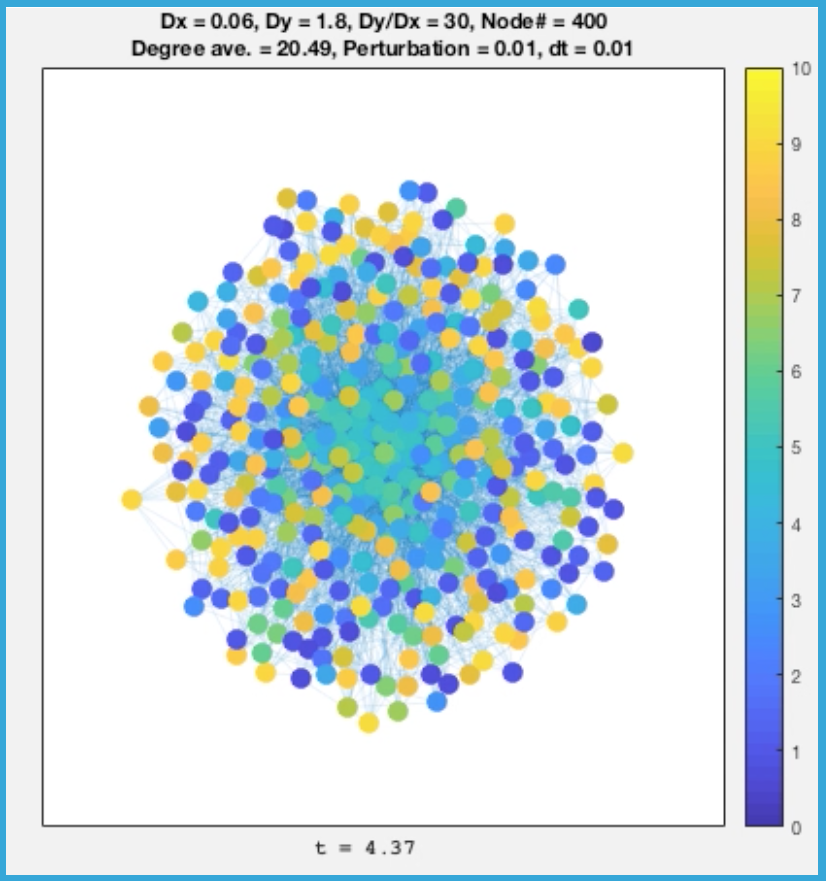
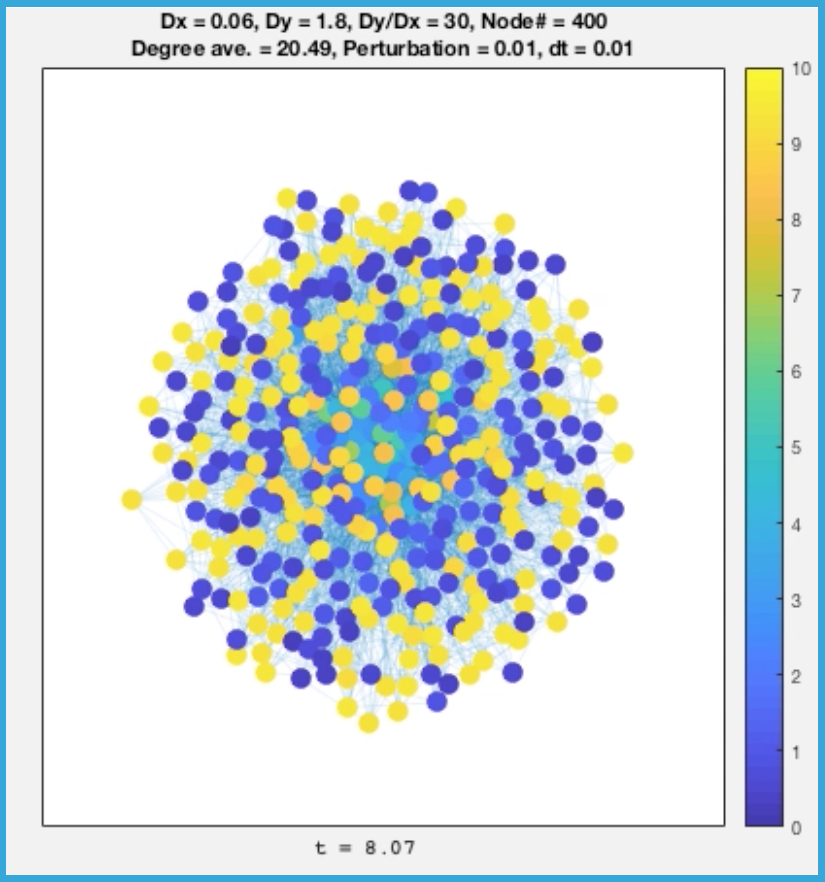
がっつり0を超えるような$\lambda_\pm^{[\alpha]}$があることがわかる。つまりこの条件下でSimulateすると、一様な定常解に加えた揺らぎは時間とともに発達してパターンを成すことがわかる。では、実験してみると、400個のNodeを持つScale Freee Network上で行うと
こんな感じで理論どおりパターンができる。
以下にSimulationを載せる。なお、4次のRunge-KuttaでSimulationした。
startSize = 2;
m = 11;
N = 400;
DyoDx = 30.0;
Dx = 0.06;
Dy = DyoDx * Dx;
dt = 0.01;
epsilon = 0;
randWidth = 0.01;
graph = scalefreenetwork(startSize, m, N);
x = 5 * ones(N, 1) + (rand(N, 1) - 0.5 * ones(N, 1)) * randWidth;
y = 10 * ones(N, 1) + (rand(N, 1)- 0.5 * ones(N, 1)) * randWidth;
colormap(jet);
for t = 0 : 1000
prevX = x;
[x, y] = nextXYRK(x, y, dt, L, Dx, Dy);
plot(graph, 'LineWidth', 0.2, 'EdgeAlpha', 0.1, 'MarkerSize', 10, ...
'NodeCData', x, 'Layout', 'force');
xticks([]);
yticks([]);
time = strcat("t = ", string(t * dt), " 1");
time = extractBefore(time, 12);
xlabel(time, 'FontName', 'FixedWidth', 'FontWeight', 'Bold');
title({data1; data2});
caxis([0, 10]);
colorbar
if (diff < epsilon & t > 200)
break;
end
pause(0.00001);
end
% this calculates next (x, y) with Runge-Kutta
function [nextX, nextY] = nextXYRK(x, y, dt, L, Dx, Dy)
k1x = f(x, y) + Dx * L * x;
k1y = g(x, y) + Dy * L * y;
k2x = f(x + dt / 2 * k1x, y + dt / 2 * k1y) +...
Dx * L * (x + dt / 2 * k1x);
k2y = f(x + dt / 2 * k1x, y + dt / 2 * k1y) +...
Dy * L * (y + dt / 2 * k1y);
k3x = f(x + dt / 2 * k2x, y + dt / 2 * k2y) +...
Dx * L * (x + dt / 2 * k2x);
k3y = f(x + dt / 2 * k2x, y + dt / 2 * k2y) +...
Dy * L * (y + dt / 2 * k2y);
k4x = f(x + dt * k3x, y + dt * k3y) +...
Dx * L * (x + dt * k3x);
k4y = f(x + dt * k3x, y + dt * k3y) +...
Dy * L * (y + dt * k3y);
nextX = x + dt / 6 * (k1x + 2 * k2x + 2 * k3x + k4x);
nextY = y + dt / 6 * (k1y + 2 * k2y + 2 * k3y + k4y);
end
function res = f(x, y)
c = 35 * ones(size(x, 1), 1);
res = x .* (1 / 9 * (c + 16 * x - x.^2) - y);
end
function res = g(x, y)
c = ones(size(x, 1), 1);
res = -((c + 2 / 5 * y) - x) .* y;
end
結論
Network上の反応拡散方程式を定義し、その性質を見た。