はじめに
明治大学総合数理学部 Advent Calenderの3日目の記事です。3日目にしてまた初日と同じ人です。それもそのはず、かなり突発的に始まった企画なので(11月30日の午前1時頃発足)参加者を全然確保できない。いっそ開き直ってNetwork関連のことを連載していこうかという次第です。技術的なお話かどうかは保証できません。
目標
Network上のLaplacianの性質を見ていくツアー。Scale Free Network号に乗って紹介していく。
(注) NetworkとGraphは同じ意で使います。
前提知識
- 微積分
- 線形代数
- 前回の話
Laplacian
数学をかじったことあるなら誰でも触れるであろうLaplacian。初めて出会うのはきっとベクトル解析の講義だと思う。普通の2次元の直交座標系ならば$\Delta$をLaplacianとして、$$\Delta = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y ^2}$$って感じで定義される。これを極座標系で考えたり、球面座標系で考えると変数変換したりしてめんどくさい式変形を駆使して、それぞれの座標系に対応したLaplacianを導出する、っていうのは理工系でも理系でも一度は通る道、なはず。
こんなのどこで使うんだって気持ちになるが、威力を発揮するのは偏微分方程式を習ったとき。拡散方程式なるものが次のように定義される。$$\frac{\partial u}{\partial t} = D \Delta u$$なんだかシンプルな式だけど、これ一つで色んな現象が表せる。匂いの拡散、熱の伝播、エネルギーが伝わるetc...
これらに共通することは**「時間と共に何かが拡散」**するということ。この拡散を表現する役目を担っているのがLaplacianなのである。
GraphのLaplacian
上で定義したLaplacianは3次元空間上の拡散現象を表すわけだが、この「空間」というものは我々の周りにはもっと色んな種類のものがある。それがNetworkである。例えばインターネット上でコンピュータウイルスが伝播する状況だったり、飛行機で人が色んな国に行ったり来たりして拡散していく状況だったりと、上の所謂普通の拡散方程式では表現できないものは沢山ある。だからNetwork上のLaplacianを定義してNetwork上の拡散方程式を定義しようじゃないか、というお話なのである。
次のようなちっちゃい無向Graph(エッジに向きや重みがない)を具体例にとって考えよう。
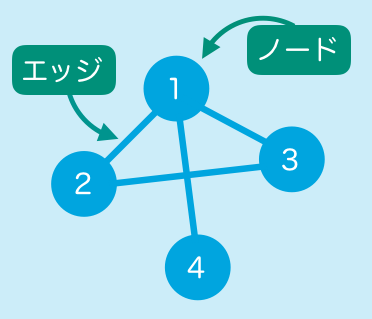
これには隣接行列というものが定義される。
A = \left(\begin{matrix}
0 & 1 & 1 & 1 \\
1 & 0 & 1 & 0 \\
1 & 1 & 0 & 0 \\
1 & 0 & 0 & 0
\end{matrix}\right)
って具合で、あるノード$i$からあるノード$j$に向かってエッジが出ていれば隣接行列の$i$行$j$列成分を1として、出ていなければ0とする簡単なお仕事。
また、次数というものも定義される。これはあるノードからどれだけエッジが出ているかを数える。$$k_1 = 3, k_2 = 2, k_3 = 2, k_4 = 1$$という感じ。もしこの数がノードのラベルに対して降順じゃなかったら、降順になるようにノードのラベルを付け替える。(この例ではその必要はない)これを対角成分に並べた行列
K = \left(\begin{matrix}
3 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{matrix}\right)
とする。
以上のことを使って、GraphのLaplacianが次のように定義できる。
L = A - K = \left(\begin{matrix}
0 & 1 & 1 & 1 \\
1 & 0 & 1 & 0 \\
1 & 1 & 0 & 0 \\
1 & 0 & 0 & 0
\end{matrix}\right) -
\left(\begin{matrix}
3 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{matrix}\right) =
\left(\begin{matrix}
-3 & 1 & 1 & 1 \\
1 & -2 & 1 & 0 \\
1 & 1 & -2 & 0 \\
1 & 0 & 0 & -1
\end{matrix}\right)
(文献によっては$L = K - A$としているところもあります。)
要するにGraph上のLaplacianは
- どのノード同士がつながっているか
- そのノードがどれくらいのノードとつながっているか
の情報を含んでいる。
これがどうしてLaplacianと呼ばれるかは次の機会に見るとして、このLaplacian行列の性質を見ていこう。
無向GraphのLaplacianの性質
ここでは線形代数の知識をフル活用して無向GraphのLaplacian行列の性質を見ていく。カンニングできるようにさっきの具体例を下に置いておく。どこかの誰かが言っていた。「例示は理解の試金石」
L =
\left(\begin{matrix}
-3 & 1 & 1 & 1 \\
1 & -2 & 1 & 0 \\
1 & 1 & -2 & 0 \\
1 & 0 & 0 & -1
\end{matrix}\right)
ざっと列挙する。
- Laplacian行列は実対称行列
- つまりは固有値が全て実数
- つまりは固有ベクトルが全部正規直交するように取れる
- Laplacian行列は半負定値行列
- つまりは1と合わせて、固有値は全て0以下
- Laplacian行列は非正則
- これは全部の行を足すと全部0になることからわかる
- Laplacian行列の固有値はGraphの連結成分だけ0がある
- 少なくとも1つ0固有値があるのは3からわかる
こんな感じ。これらの中で自明でないのは2番と4番。**証明は読者の演習とする。**この言葉は数学書では随所に見られて、著者がサボったか、本当に読者のことを思っているかのどちらかである。
Graph Laplacianの固有値と固有ベクトル
上の性質の中で一番面白いのは固有値と固有ベクトルのお話。ノード数1000のScale Free NetworkのLaplacianを取ってきて、その固有値を降順に並べてプロットしてみるとこんな感じになる。縦軸が固有値で、横軸が降順に並べた時の固有値の番号。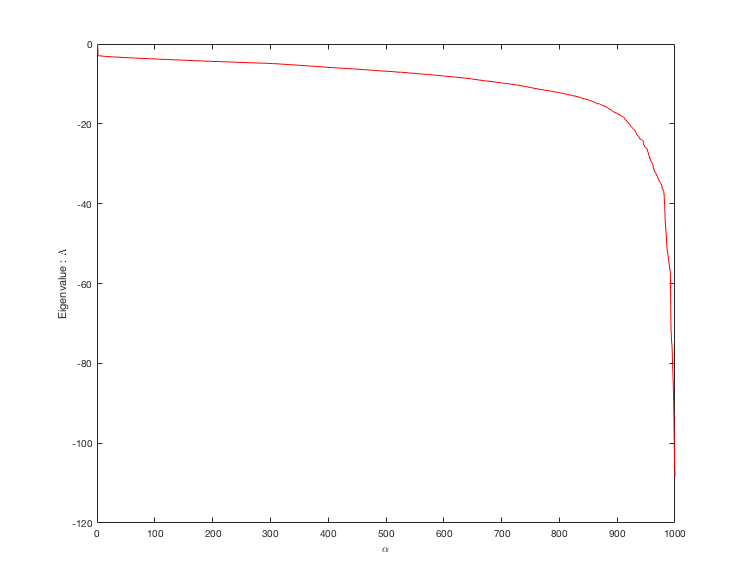
これを見ると、だいたい900くらいからがくっと落ちているのがわかる。これはパラメータを変えても大体ここらへんでがくっと落ちる。
もっと面白いのは固有ベクトル。降順に並べた固有値のうち、25, 250, 500, 750, 975番目に対応する固有ベクトルを取ってきて、この成分を横に並べて見てみたのが下の図。
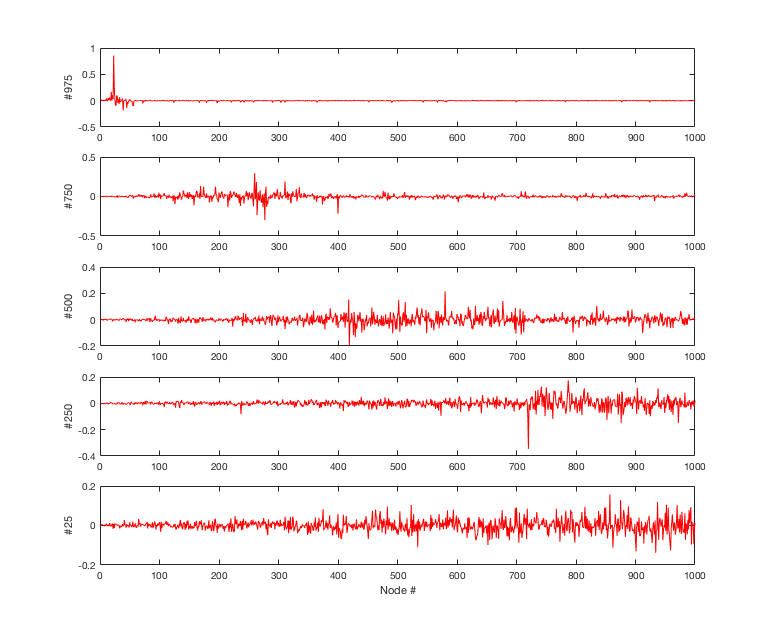
なんだか各固有ベクトルにおいて成分が局在している様子が見える。
未解決問題
固有ベクトルの局在性は数学的には未解決問題である。実際に実験してみれば、ああそうだねとなるが、数学ではそれは何も意味しない。きちんとした数学的な論理を使って証明しないと、数学的に正しいとはいえないのである。じゃあ何が難しいのかと言われると、数学には固有ベクトルを扱えるような理論がまだ確立されていないのである。固有値を研究するなら関数解析の一分野でもあるスペクトル理論を使えば良いのだが、固有ベクトルともなると何とも。一応、摂動論という理論を使って証明は試みられたが、失敗に終わったようである。なんとかGraphの連続極限を取って、作用素としてみなし、その固有関数を見れば行けそうな気がするが、それも果たしてどうなのかはわからない。
結論
Network上のLaplacianを定義してその性質を見た。