Strawberry Fieldsで光量子計算をする(その7) 測定・フィードフォワード型量子計算

$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$

前置き

量子計算を行う物理系として、
光は常温でも量子状態を取り出すことができてかつ長距離伝送に比較的適しているという嬉しい性質があるのですが、常に問題になるのが「(量子的なレベルで)非線形な操作が難しい」ことです。

ただ非線形と言うとあまりに一般的でなんのこっちゃともなりますが、どシンプルに言うと例えば「入力された光の光子数が1個だったら何もしない、2個だったら位相を反転する」操作を実現するために必要な性質です。

上の例なら光の強度によって位相の回転度合いが変わる物質が必要で、それ自体は"非線形"光学結晶など普通に存在します。
問題はその度合いで、そうした強い"非線形性"を実現することが光による量子計算における大きな課題だったりします。

…という課題と、非線形性をどうクリアするかに対する1つの有望なアプローチがこちらの文献に良い感じでまとまっています。
キーワードは大きく2つで
- 測定型量子計算
- クラスター状態
とのこと。

測定・フィードフォワード型量子計算は入力光と補助ビットに対する適切なゲート操作と測定、および測定値のフィードフォワードによって実現します。こちらのCV量子テレポーテーションもそれにあたると思います。
重要なのは、
- 適切な補助ビットを用意することでテレポーテーションだけでなく非ガウスゲートを含むユニタリ変換が可能
- 補助ビットの生成は確率的でもターゲットのqumodeに対するゲート操作は決定論的に行える
という点です。
要するに、適切な状態の補助ビットを確率的にでも用意できれば、原理的には決定論的なユニバーサル量子ゲートができます。
(こちらの2章-Bより)

今回は測定・フィードフォワード型量子計算の簡単な例を少し詳しくやります。

測定・フィードフォワード型量子計算

まずはこちらのCV量子テレポーテーションを直交位相状態を計算することで追っていきます。
(慎重に計算していますが、もし誤りに気づいたら指摘頂けるととても助かります)

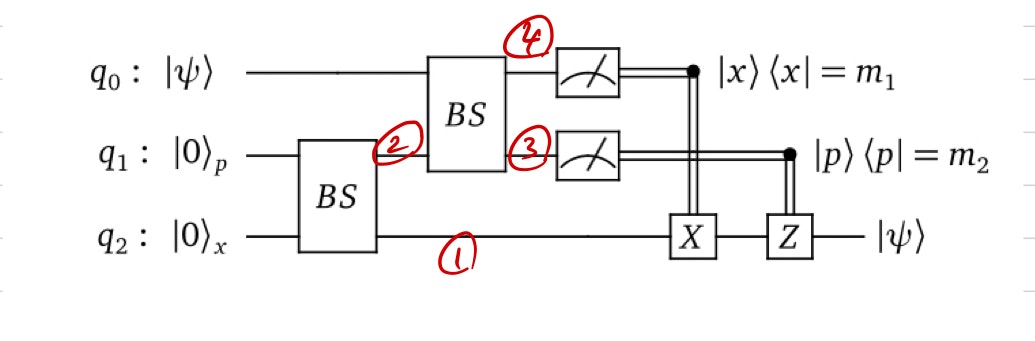
量子回路はこうでした。
(https://strawberryfields.readthedocs.io/en/latest/algorithms/teleportation.html)

…手書きが汚くて申し訳ないです。

$q_0$, $q_1$, $q_2$の直交位相状態をそれぞれ$\hat{x_0}$, $\hat{p_0}$, $\hat{x_1}$, $\hat{p_1}$, $\hat{x_2}$, $\hat{p_2}$とします。
$q_1$, $q_2$はそれぞれスクイーズド状態のため、さらに以下のように書けます。
上付きの$vac$は真空場状態を表します。

\hat{x_1} = \hat{x_{1}^{vac}}e^r \\
\hat{p_1} = \hat{p_{1}^{vac}}e^{-r} \\
\hat{x_2} = \hat{x_{2}^{vac}}e^{-r} \\
\hat{p_2} = \hat{p_{2}^{vac}}e^{r}

①, ②, ③, ④の状態をそれぞれ上付き添字(1)~(4)で表すと、以下のようになります。

\hat{x^{(1)}} = \frac{1}{\sqrt{2}}(\hat{x_2}+\hat{x_1}) = \frac{1}{\sqrt{2}}(\hat{x_{2}^{vac}}e^{-r} + \hat{x_{1}^{vac}}e^r) \\

\hat{p^{(1)}} = \frac{1}{\sqrt{2}}(\hat{p_2}+\hat{p_1}) = \frac{1}{\sqrt{2}}(\hat{p_{2}^{vac}}e^{r} + \hat{p_{1}^{vac}}e^{-r}) \\

\hat{x^{(2)}} = \frac{1}{\sqrt{2}}(\hat{x_2}-\hat{x_1}) = \frac{1}{\sqrt{2}}(\hat{x_{2}^{vac}}e^{-r} - \hat{x_{1}^{vac}}e^r) \\

\hat{p^{(2)}} = \frac{1}{\sqrt{2}}(\hat{p_2}-\hat{p_1}) = \frac{1}{\sqrt{2}}(\hat{p_{2}^{vac}}e^{r} - \hat{p_{1}^{vac}}e^{-r}) \\

\hat{x^{(3)}} = \frac{1}{\sqrt{2}}(\hat{x_0}-\hat{x^{(2)}}) = \frac{1}{\sqrt{2}} \hat{x_{0}} - \frac{1}{2}\hat{x_{2}^{vac}}e^{-r} + \frac{1}{2}\hat{x_{1}^{vac}}e^{r} \\

\hat{p^{(3)}} = \frac{1}{\sqrt{2}}(\hat{p_0}-\hat{p^{(2)}}) = \frac{1}{\sqrt{2}} \hat{p_{0}} - \frac{1}{2}\hat{p_{2}^{vac}}e^{r} + \frac{1}{2}\hat{p_{1}^{vac}}e^{-r} \\

\hat{x^{(4)}} = \frac{1}{\sqrt{2}}(\hat{x_0} + \hat{x^{(2)}}) = \frac{1}{\sqrt{2}} \hat{x_{0}} + \frac{1}{2}\hat{x_{2}^{vac}}e^{-r} - \frac{1}{2}\hat{x_{1}^{vac}}e^{r} \\

\hat{p^{(4)}} = \frac{1}{\sqrt{2}}(\hat{p_0} + \hat{p^{(2)}}) = \frac{1}{\sqrt{2}} \hat{p_{0}} + \frac{1}{2}\hat{p_{2}^{vac}}e^{r} - \frac{1}{2}\hat{p_{1}^{vac}}e^{-r} \\

最後に③の運動量状態と④の位置状態を測定し、$\sqrt{2}$のファクターをかけて①に対してdisplacement操作を行えば、スクイージングパラメータ$r$を無限に大きい極限で出力は$q_0 (\hat{x_{0}}, \hat{p_{0}})$に無限に近づきます。

\hat{x^{(1)}} + \sqrt{2}\hat{x^{(4)}} = \hat{x_{0}} + \sqrt{2}\hat{x_{2}^{vac}}e^{-r} \to \hat{x_{0}} \\
\hat{p^{(1)}} + \sqrt{2}\hat{p^{(3)}} = \hat{p_{0}} + \sqrt{2}\hat{p_{1}^{vac}}e^{-r} \to \hat{p_{0}}

これならまだ簡単ですね。
strawberry fieldsでの実行はこちらで行っているので省略します。

もうひとつ、入力光に対しスクイーズを行う測定・フィードフォワード型スクイージングゲートを勉強してみます。
任意の入力光に対するスクイージングゲートはこの手の量子計算スキームで頻出する割に実装が難しいそうですが、この方法は比較的リーズナブルそうです。

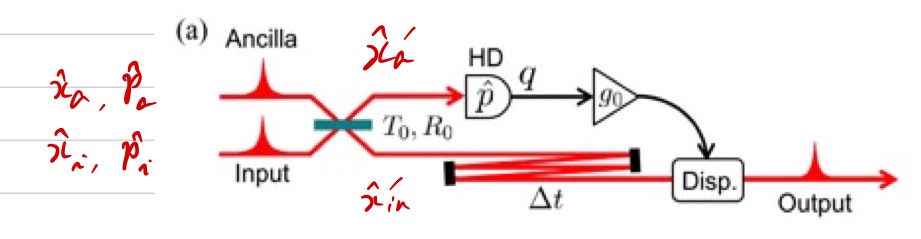
量子回路はテレポーテーションよりシンプルです。
(元の図は https://arxiv.org/abs/1706.06312 より)

$T_0$, $R_0$はビームスプリッタの透過率、反射率で$T_0+R_0=1$です。
$g_0$はフィードフォワード時のゲインで、以下の式でも示すように$g_0 = \sqrt{T_0 / R_0}$とします。
計算は先程のCV量子テレポーテーションと同様に行います。

\hat{x_a'} = \sqrt{T_0} \hat{x_{in}} - \sqrt{R_0} \hat{x_{a}} \\
\hat{p_a'} = \sqrt{T_0} \hat{p_{in}} - \sqrt{R_0} \hat{p_{a}} \\
\hat{x_{in}'} = \sqrt{R_0} \hat{x_{in}} + \sqrt{T_0} \hat{x_{a}} = \sqrt{R_0} \hat{x_{in}} + \sqrt{T_0} \hat{x_{a}^{vac}} e^{-r} \to \sqrt{R_0} \hat{x_{in}} \\
\hat{p_{in}'} = \sqrt{R_0} \hat{p_{in}} + \sqrt{T_0} \hat{p_{a}} =  \sqrt{R_0} \hat{p_{in}} + \sqrt{T_0} \hat{p_{a}^{vac}}e^r \\

$\hat{p_{in}'}$に対し、$\hat{p_a'}$の測定結果をもとにdisplacementを行います。

\begin{align}
\hat{p_{in}''} &= \hat{p_{in}'} + g_0 \hat{p_a'} \\
&= \sqrt{R_0} \hat{p_{in}} + \sqrt{T_0} \hat{p_{a}} + \sqrt{\frac{T_0}{R_0}}(\sqrt{T_0} \hat{p_{in}} - \sqrt{R_0} \hat{p_{a}}) \\
&= \frac{1}{\sqrt{R_0}} \hat{p_{in}}
\end{align}

結果として、この量子回路の出力は$\hat{x_{in}'}$, $\hat{p_{in}''}$です。
以上からわかるように、
- スクイージングレベルはビームスプリッタの反射率によって決まります
- Ancillaのスクイージングレベルを上げると、Output $\hat{x_{in}'}$と入力$\hat{x_{in}}$の誤差を無限に小さくできます
- $0 < R_0 < 1$なので$\hat{x}$方向にスクイーズされます
　(単純な変更で$\hat{p}$方向も実現可能だと思います)

最後にstrawberry fieldでの実装例です。
$\sqrt{R_0}=\frac{1}{2}$としています。

import strawberryfields as sf
from strawberryfields.ops import *
from strawberryfields.utils import scale
from numpy import pi, sqrt
import matplotlib.pyplot as plt
import numpy as np

eng, q = sf.Engine(2)

x_ini = 1
p_ini = 1
r = 3
R0 = 1/4
T0 = 1 - R0
theta = np.arccos(np.sqrt(R0))
g0 = np.sqrt(T0/R0)

with eng:
    # prepare the initial states
    Coherent(x_ini/2 + p_ini/2 * 1j) | q[0]  # input (arbite)
    Sgate(r) | q[1] # Ancilla (position squeezed if r>0)

    # apply the gates
    BSgate(theta, 0) | (q[0], q[1])  # a 50-50 beamsplitter

    # perform the homodyne measurements
    MeasureP | q[1]

    # displacement gates conditioned on the measurements
    Zgate(scale(q[1], g0)) | q[0]

state = eng.run('gaussian')
mu, cov = state.reduced_gaussian([0])
x = np.arange(-3*x_ini-5, 3*x_ini+5, 0.1)
p = np.arange(-3*p_ini-5, 3*p_ini+5, 0.1)
W = state.wigner(0, x, p)
X, P = np.meshgrid(x, p)
plt.contourf(X, P, W)

print(mu)
print(cov)

[実行結果]

[0.5        1.99380578]
[[2.51859057e-01 4.53595607e-17]
 [4.53595607e-17 3.97047465e+00]]

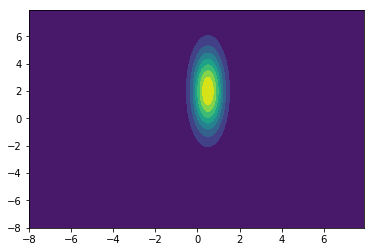
ウィグナー関数のプロットを見ると、ちゃんとスクイージング出来てますね。

$\sqrt{R_0}=\frac{1}{2}$に対し直交位相座標が2のファクターで、分散が$2^2=4$のファクターで変化しているので妥当そうです。

余談なのですが、

Coherent(x_ini/2 + p_ini/2 * 1j)

の仕様に少しはまりました。
上のようにファクター1/2をかけて入力を与えないと測定値の平均が($\hat{x}, \hat{p}$)=(x_ini, p_ini)となりません。
つまり内部でファクター2がかかっているようです。意図まではわかりませんでした。
(https://strawberryfields.readthedocs.io/en/latest/conventions/states.html#coherent-state の"Coherent State"を見ると確かにそうなってるっぽい)

まとめ

測定・フィードフォワード型量子計算の概要と簡単な例の計算、strawberry fieldsによるハンズオンをすることができました。
この基本的な流れを抑えて、より複雑なゲート操作も頭に入れていきたいですね。

以上、最後までありがとうございました。

参考にした文献

• Akira Furusawa, Peter van Loock, "Quantum Teleportation and Entanglement: A Hybrid Approach to Optical Quantum Information Processing", WILEY
• https://arxiv.org/abs/1706.06312
• https://strawberryfields.readthedocs.io/en/latest/algorithms/teleportation.html
• https://aip.scitation.org/doi/10.1063/1.5100160