$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
今回は量子テレポーテーションです。
{$\ket{0},\ket{1}$}基底の離散量子テレポーテーションと同様に、連続量状態についても量子テレポーテーションが可能です。
今回も公式のドキュメントから図など引用していきます。
(気のせいか公式ドキュメントのコンテンツが増えてるような気がして、このペースだと紹介より早く増えていくんじゃ...と思ったのでさくっといきます。)
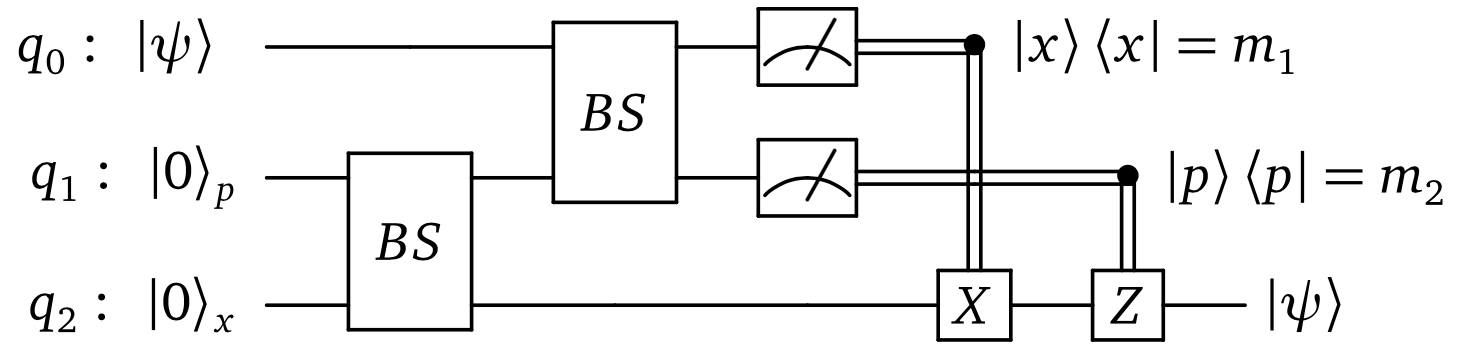
$q_0$がテレポートさせたい状態です。
最初にそれぞれ運動量方向、位置方向に強くスクイーズさせた$q_1$, $q_2$を用意します。
次に、BS(Beam Splitter)で$q_1$, $q_2$をエンタングルさせてからAliceとBobで分け合います。
次にAliceは手元の$q_1$と$q_0$をエンタングルさせた後にそれぞれの$\hat{x}, \hat{p}$について測定し、Bobは古典チャンネルで受け取った測定結果をもとに手元の$q_2$にXゲート、Zゲートを作用させます。
その結果、$q_2$に$q_0$の状態がコピーされます。
コードで見てみましょう。
公式のサンプルコードと大体一緒です。jupyter notebookで作っています。
ただし、
- テレポーテーションがどの程度正確に行われているかチェックするため、本来は不要な4つ目のqumodeを1つ目のqumodesと全く同じ状態で用意しています
- $q_1$と$q_2$のスクイージングレベルを変数にしています
import strawberryfields as sf
from strawberryfields.ops import *
from strawberryfields.utils import scale
from numpy import pi, sqrt
import matplotlib.pyplot as plt
eng_g, q_g = sf.Engine(4)
r = 2 #squeeze Level
x_ini = 1
p_ini = 0.5
with eng_g:
# prepare the initial states
Coherent(x_ini + p_ini * 1j) | q_g[0] # This is the state we will teleport
Sgate(-r) | q_g[1] # momentum squeezed
Sgate(r) | q_g[2] # position squeezed
Coherent(x_ini + p_ini * 1j) | q_g[3] # Same state as q[0] for check
# apply the gates
BSgate(pi/4, 0) | (q_g[1], q_g[2]) # a 50-50 beamsplitter
BSgate(pi/4, 0) | (q_g[0], q_g[1]) # a 50-50 beamsplitter
# perform the homodyne measurements
MeasureX | q_g[0]
MeasureP | q_g[1]
# displacement gates conditioned on the measurements
Xgate(scale(q_g[0], sqrt(2))) | q_g[2]
Zgate(scale(q_g[1], sqrt(2))) | q_g[2]
state_g = eng_g.run('gaussian')
print("telepoted state's mean of x and p")
print(state_g.means()[2], state_g.means()[6])
print("original state's mean of x and p")
print(state_g.means()[3], state_g.means()[7])
x = np.arange(-5, 5, 0.1)
p = np.arange(-5, 5, 0.1)
W_g = state_g.wigner(2, x, p)
X, P = np.meshgrid(x, p)
plt.contourf(X, P, W_g)
後半部、state_g.means()に演算実行後の各qumodesのWigner関数における$\hat{x}, \hat{p}$の平均値が格納されます。
(Wigner関数におけるGaussianも、平均と分散でパラメタライズされる点で古典確率分布のGaussianと同じです)
ここでは最初にAliceの手元にあった状態と同一の状態(q[0])と、Bobの手元にテレポーテーションされた状態q[2]について書き出し、比較可能にしています。
最後に、q[2]をプロットしています。見慣れたGaussianっぽい見た目をしています。
:プロット出力例
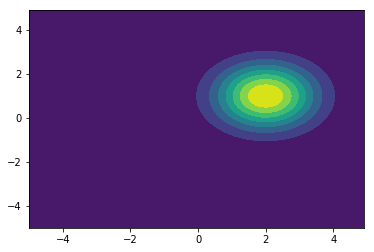
q[3]をプロットする場合は以下のコードを追加で実行してください。
大体同じような分布形状になります。
x1 = np.arange(-5, 5, 0.1)
p1 = np.arange(-5, 5, 0.1)
W_ini = state_g.wigner(3, x1, p1)
X1, P1 = np.meshgrid(x1, p1)
plt.contourf(X1, P1, W_ini)
q[0]とq[2]の比較は、例えば以下のように出力されると思います。
telepoted state's mean of x and p
2.271047597290189 1.2010071386881478
original state's mean of x and p
2.0 1.0
少しずれていますが、これはq[0]とq[1]の測定値がばらつくためです。
初期状態として用意したスクイーズド状態のスクイージングレベルが有限のため、測定値にも一定のばらつきが生じます。
ばらつきの範囲内で、テレポート後の値は実行の都度変化します。
どの程度の精度が必要かはさておき、試しに9行目でr=10にしてスクイージングレベルを上げてみましょう。
telepoted state's mean of x and p
1.9999909715888862 1.0003976026910095
original state's mean of x and p
2.0 1.0
相当精度が良くなりましたね。
r=2で18dB程度のスクイージングに相当すると、チュートリアルに記載があります。
($e^{-r}$でスケールされるので大体そんなものでしょう)
2014年の某F研究室のD論によると、当時実験的には9dBでトップレベルですので、r=2は相当頑張ってる値だと私は推測しています。正確な所は詳しくないですが...。
どの道、現実に無限のスクイーズレベルを達成するには無限のエネルギーが必要なためどこか良い塩梅で近似するのです。
まとめ
量子テレポーテーションができました。コードで実行してみるとあっさりです。
ただ、量子テレポーテーションは要素技術であってまだ実社会の課題に役立ちそうな気がしてきません。
先は長いです。生き急いでいきましょう。