$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
趣旨
量子アルゴリズムって、割と基本的なものでも数式を追っていくと頭痛くなるほど難しくて、私は正直理解できてるのかよくわからなくなるんですよね。
あれだけAPIが充実した機械学習界隈でも代表的なアルゴリズムを一度は自分で書くべきと言われてるのだから、量子アルゴリズムもかくあるべきなのではないでしょうかと。
GUIはお手軽で楽しいですが、自分で実装したコードが狙い通りの出力をする快感には敵いません。
というわけで、ふわっと量子フーリエ変換のnumpy実装にトライしました。
ほぼ確実に車輪の再発明ですけど、参考になればと思います。
素人実装な部分は大目に見てください...。
数式
まずは https://whyitsso.net/physics/quantum_mechanics/QFT.html から抜粋させて頂きながら、量子フーリエ変換の数式を確認していきます。
入力n-qubit列$\ket{x}$が以下のように与えられるとしましょう。
$\ket{x} = \sum^{N-1}_{j=0} x_j \ket{j}$
$(N = 2^n)$
ここで$\ket{x}, \ket{j}$はqubit列で表される2進数の10進表記で考えます。
どういうことかと言うと、例えば $\ket{j}$が2-qubits状態 $\ket{10}$の場合、$\ket{j} = \ket{2}$と書くものとします。
もう少し書くと、
$$
\begin{align}
\sum^{3}_{j=0} x_j \ket{j} &= x_0 \ket{0}+x_1 \ket{1}+x_2 \ket{2}+x_3 \ket{3} \\
&= x_0 \ket{00}+x_1 \ket{01}+x_2 \ket{10}+x_3 \ket{11}
\end{align}
$$
という感じです。
ここで各状態ベクトル $x_j \ket{j}$が離散フーリエ変換の入力データ点の1つとみなせるため、離散フーリエ変換の定式を用いて以下のように式展開できます。
(元々フーリエ変換が関数ベクトルの変換だったと考えると、量子フーリエ変換は量子状態ベクトルの変換をフーリエ変換と同じ作法で行っていると思えば良いと考えています)
\begin{align}
\ket{y} &= \sum^{N-1}_{k=0} y_k \ket{k} \\\
&= \sum^{N-1}_{k=0} [\frac{1}{\sqrt{N}} \sum^{N-1}_{j=0} \exp(i \frac{2\pi kj}{N})\ x_j] \ket{k}\\
&=\sum^{N-1}_{j=0}x_j\ [\frac{1}{\sqrt{N}} \sum^{N-1}_{k=0} \exp{(i\frac{2\pi kj}{N})}\ \ket{k} ]
\end{align}
ここでは変換後の状態ベクトル$\ket{y}$の係数$y_k$に、離散フーリエ変換の定式
$y_{k} = \frac{1}{\sqrt{N}} \sum^{N-1}_{j=0} \exp (i \frac{2 \pi kj}{N}) x_j$
を代入しました。
すると、入力qubit列 $\ket{x} = \sum^{N-1}_{j=0} x_j \ket{j}$ の各$\ket{j}$について次のような変換が成り立つことがわかります。
$\ket{j}\ \to \frac{1}{\sqrt{N}} \sum^{N-1}_{k=0} \exp{(i\frac{2\pi kj}{N})}\ \ket{k} \tag{1}$
これで、量子状態ベクトルに対してのフーリエ変換が定式化できました。
この変換ですが、実は次式のように書き換えることができます。
$$
\begin{align}
\ket{j} &\to \frac{1}{\sqrt{2^n}}(|0>+e^{i2\pi 0.j_0}|1>)(|0>+e^{i2\pi 0.j_1 j_0}|1>)\cdots (|0>+e^{i2\pi 0.j_{n-1} j_{n-2} \cdots j_0}|1>) \tag{2}
\end{align}
$$
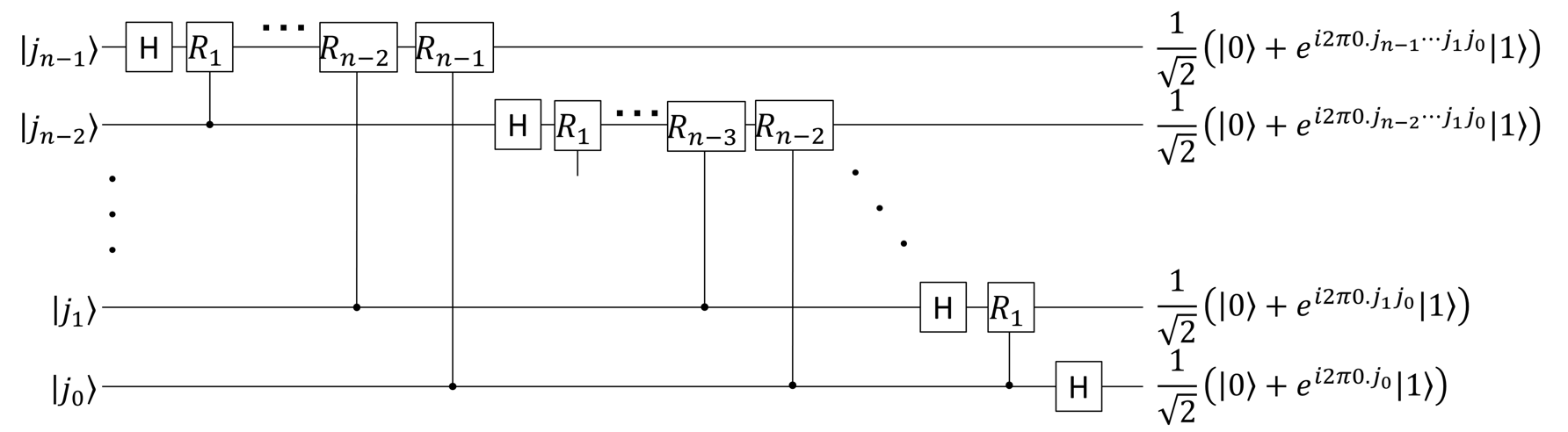
すると、下図のような量子ゲート回路で実装が可能なようです。
(https://whyitsso.net/physics/quantum_mechanics/QFT.html より引用)
$H$ゲートはアダマールゲート
H=
\begin{pmatrix}
1 & 1 \\
1 & -1
\end{pmatrix}
$R_k$ゲートは下記のような量子ゲートです。
R_k =
\begin{pmatrix}
1 & 0 \\
0 & e^{i \pi/2^{k}}
\end{pmatrix}
bit数が増えても$H$ゲートと$R_k$ゲートを使った繰り返し処理で一般化できる形になっていますね。
実装
今回は式$(1)$と式$(2)$でそれぞれ量子フーリエ変換の出力を確認します。
(当然一致するはずです)
式(1)は解析的な計算、式(2)は量子ゲート回路を模倣した計算、と考えています。
まずは式(1)の実装です(jupyter notebookで確認)。
入力状態は$\ket{10}$をリスト[1, 0]として与えています。
import numpy as np
def binToInt(inputState):
out = 0
for i in range(len(inputState)):
out += inputState[-1-i]* 2**i
return out
def QFT_calc(inputState):
j = binToInt(inputState)
N = 2 ** len(inputState)
calc = []
for i in range(N):
calc.append(1/np.sqrt(N) * np.exp(1j * 2*np.pi *i*j / N))
return calc
inputState = [1,0]
calc = QFT_calc(inputState)
print(np.round(calc,3))
以下のような出力になりました。
これくらいなら手計算でも簡単に確認できますね。
[ 0.5+0.j -0.5+0.j 0.5-0.j -0.5+0.j]
次に式(2)の実装です。
少し長いですが、本体は最下部の"QFT"関数です。
import numpy as np
class Qbits:
def __init__(self, initial):
self.states = []
for i in range(len(initial)):
if initial[i]==1:# |1>
self.states.append(np.array([0+0j,1+0j]))
else:
self.states.append(np.array([1+0j,0+0j]))
def tensorProd(self, a, b):
dim_a = len(a)
dim_b = len(b)
k = np.zeros(dim_a*dim_b) + 0j
ite = 0
for i in range(dim_a):
for j in range(dim_b):
k[ite] = a[i]*b[j]
ite += 1
return k
def outputTensorProduct(self):
out = self.states[0]
for i in range(1, len(self.states)):
out = self.tensorProd(out, self.states[i])
return out
def Hadamard(self, i):
H = np.array([[1,1],[1,-1]]) / np.sqrt(2)
self.states[i] = np.dot(H, self.states[i])
def C_Hadamard(self, c, i):
if self.states[c] == np.array([1,0]):
self.Hadamard(i)
def Rphase(self, i, k):
R = np.array([[1,0],[0,np.exp(1j * np.pi / (2**k))]]) + 0j
self.states[i] = np.dot(R, self.states[i])
def C_Rphase(self, c, i, k):
if self.states[c][1] == 1+0j:
self.Rphase(i, k)
def flipState(self):
self.states.reverse()
def QFT(initial):
A = Qbits(initial = initial)
N = len(initial)
for i in range(N):
for j in range(i):
A.C_Rphase(i, j, i-j)
A.Hadamard(i)
A.flipState()
return A.outputTensorProduct()
inputState = [1,0]
a = QFT(initial = inputState)
print(np.round(a,3))
先程のコードと同じ入力状態を与えているため、出力も同じとなるはずです。
[ 0.5+0.j -0.5+0.j 0.5+0.j -0.5+0.j]
inputStateは"0"または"1"のみを要素にもつリストであれば動くはずです。
例えばもっと長いqubit列を用意して、両実装の比較をすると
inputState = [1,0,1,0]
calc = QFT_calc(inputState)
print(np.round(calc,3))
a = QFT(initial = inputState)
print(np.round(a,3))
出力は以下のように等しくなります。
[ 0.25 +0.j -0.177-0.177j 0. +0.25j 0.177-0.177j -0.25 +0.j
0.177+0.177j -0. -0.25j -0.177+0.177j 0.25 -0.j -0.177-0.177j
-0. +0.25j 0.177-0.177j -0.25 +0.j 0.177+0.177j -0. -0.25j
-0.177+0.177j]
[ 0.25 +0.j -0.177-0.177j 0. +0.25j 0.177-0.177j -0.25 +0.j
0.177+0.177j -0. -0.25j -0.177+0.177j 0.25 +0.j -0.177-0.177j
0. +0.25j 0.177-0.177j -0.25 +0.j 0.177+0.177j -0. -0.25j
-0.177+0.177j]
計算誤差など考慮できていないため、状態列を長くしたらボロが出るかもしれないです。
複素数の扱いも、もっと良い方法がありそうですけどとりあえず気にしない。
2通りの計算方法で検算しているので合っている...はず...。
まとめ
量子フーリエ変換をnumpyのみで実装できたと思います。
個人的には数式を読んで分かったと思っていても、実装して出力結果を突きつけられると理解が曖昧な部分があぶり出されたりして良かったです。
量子フーリエ変換はShor's Algorithmなどで重要な役割を果たすのでぜひ理解しておきたいですよね。
以上、読んで頂きありがとうございました。
参考にしたもの
- https://whyitsso.net/physics/quantum_mechanics/QFT.html
- "量子情報科学入門", 石坂 智 他, 共立出版