はじめに
下記論文のSelf-Organizing State Space Model(自己組織化型状態空間モデル)をPython実装してみました。粒子フィルタのシステムノイズ/観測ノイズに非ガウス性ノイズを仮定することで、ハイパーパラメータを自分で最適化していきます。
超パラメータの探索は結構面倒なので、勝手に最適化してくれるこいつは結構便利です。(次は超々パラメータの探索が問題になりますが…)
参考:自己組織化型状態空間モデルを用いた運動軌跡のフィルタリング
こここうした方がいいよとか間違ってね?とかあったら気軽にコメントください。
あと、よくわかんないから教えてとかでも歓迎します。
2016/12/14 修正
- ソースがごちゃごちゃしていたのを書き直し
- numpyをforで回すと遅いらしいので、リサンプリングをcythonで書き直してみた(あまり変わらず)
- cupyで動かそうとしたが、案の定うまくインストールできず無事死亡
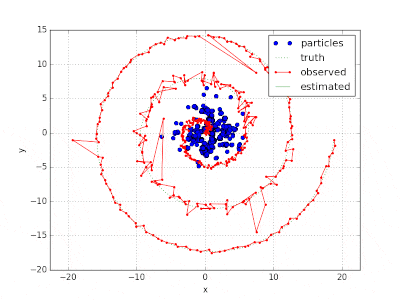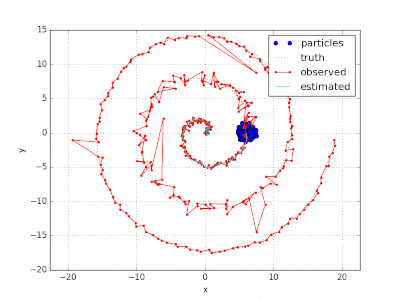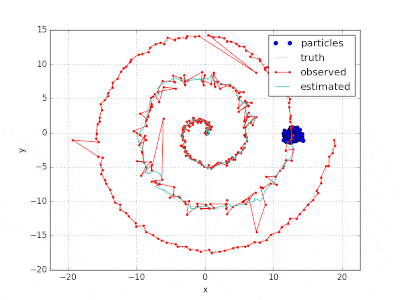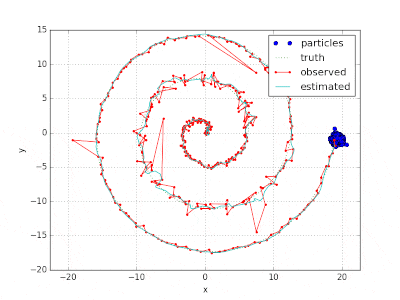
通常の粒子フィルタとの比較
どちらも、途中で雑音の分散を大きくしています。
- 通常の粒子フィルタの方は、分散が小さい領域ではうまく追従しているように見えますが、分散が大きいエリアで暴れます。
- 自己組織化型の方は、分散が大きい領域で多少粒子の広がりが大きくなり、誤差に寛容になっているようです。
粒子フィルタのPython実装 - Qiita で実装したもの
今回のもの
ソースコード
概要
- particle_selforganized.py
- test_particle_selforganized.py
注意 ユーティリティ関数とかは下記と同じです。
粒子フィルタのPython実装 - Qiita
- utils.py
- resample.pyx
粒子フィルタ本体
particle_selforganized.py
# !/usr/bin/env python
# -*- coding: utf-8 -*-
"""自己組織化型粒子フィルタのpython実装
"""
import pyximport
pyximport.install()
import resample
import numpy as xp
# import cupy as xp
def _rand_cauchy(gma):
nr, nc = gma.shape
uni = xp.random.rand(nr, nc)
return xp.arctan(uni/gma) /xp.pi + 1./2.
def _rand_normal(sgm, shape):
return xp.random.normal(0, sgm, shape)
def _logpdf_cauchy(gma, x):
y = xp.log(gma/xp.pi) -xp.log(x**2. + gma**2.)
return xp.sum(y, axis=0)
def _normalize(w):
return w / xp.sum(w)
class ParticleFilterSelfOrganized(object):
_sgm = 0.001
def __init__(self, f, h, pars_init, pars_hpt_init, pars_hpo_init):
self._f = f
self._h = h
_, num = pars_init.shape
self._num = num
self._w = _normalize(xp.ones(num))
self._pars = pars_init
self._pars_hpt = pars_hpt_init
self._pars_hpo = pars_hpo_init
def update(self, y):
self._update_pars()
self._update_weights(y)
self._resample()
def _update_pars(self):
self._pars = self._f(self._pars) + _rand_cauchy(xp.exp(self._pars_hpt/2.))
self._pars_hpt = self._pars_hpt + _rand_normal(self._sgm, self._pars_hpt.shape)
self._pars_hpo = self._pars_hpo + _rand_normal(self._sgm, self._pars_hpo.shape)
def _update_weights(self, y):
Y = y.reshape(y.size,1) * xp.ones(self._num)
pars_hpo = xp.exp(self._pars_hpo/2.)
loglh = _logpdf_cauchy( pars_hpo, xp.absolute(Y - self._h(self._pars)) )
self._w = _normalize( xp.exp( xp.log(self._w) + loglh ) )
def _resample(self):
wcum = xp.r_[0, xp.cumsum(self._w)]
num = self._num
idxs = resample.resample(num, wcum)
# start = 0
# idxs = num*[0]
# for i, n in enumerate( sorted(xp.random.rand(num)) ):
# for j in range(start, num):
# if n <= wcum[j+1]:
# idxs[i] = start = j
# break
self._pars = self._pars[:,idxs]
self._pars_hpt = self._pars_hpt[:,idxs]
self._pars_hpo = self._pars_hpo[:,idxs]
self._w = _normalize(self._w[idxs])
def estimate(self):
return xp.sum(self._pars * self._w, axis=1)
def particles(self):
return self._pars
粒子フィルタ利用側のサンプル
test_particle_selforganized.py
# !/usr/bin/env python
# -*- coding: utf-8 -*-
"""particle_selforganized.pyの利用サンプル
"""
import particle_selforganized as par
import utils
import numpy as xp
# import cupy as xp
# パラメータ設定 --------------------
num = 5000 # 粒子数
v_noise = 0.05
# 初期粒子
mins = -5. * xp.ones(4)
maxs = +5. * xp.ones(4)
pars_init = utils.rand_uniform(mins, maxs, num)
pars_hpt_init = xp.random.normal(0, 0.01, pars_init.shape)
pars_hpo_init = xp.random.normal(0, 0.01, (2,num))
# ---------------------------------
dataset = utils.load_data("testdata")
# dataset = utils.generate_data("testdata")
# 状態モデルの生成 (2次階差モデル)
A = xp.kron(xp.eye(2), xp.array([[2, -1], [1, 0]]))
f_trans = lambda X: A.dot(X)
# 観測モデルの生成 (直接観測モデル)
B = xp.kron(xp.eye(2), xp.array([1, 0]))
f_obs = lambda X: B.dot(X)
# 初期プロット
lines = utils.init_plot_particle(dataset, pars_init)
# 粒子フィルタの生成
pf = par.ParticleFilterSelfOrganized(
f_trans, f_obs, pars_init, pars_hpt_init, pars_hpo_init)
x_est = xp.zeros(dataset.x.shape)
for i, y in enumerate(dataset.y):
pf.update(y)
state = pf.estimate()
x_est[i,:] = f_obs(state)
# データのプロット
pars = pf.particles()
utils.plot_each_particle(lines, x_est, pars, i)
# utils.save_as_gif_particle(dataset, pars_init, pf, "particle_selforganized.gif")