粒子フィルタのPython実装

はじめに

ありがちなやつですが、作成したので置いておきます。
気が向いたら解説を追加します。

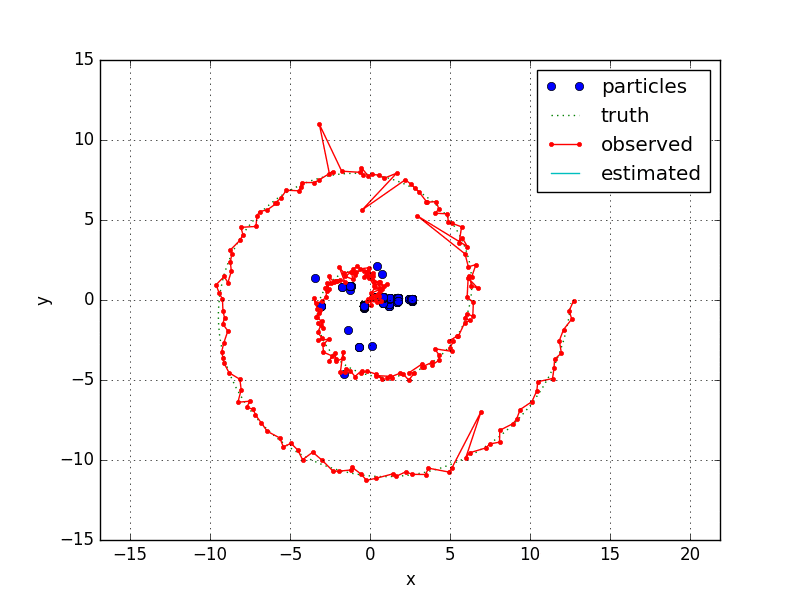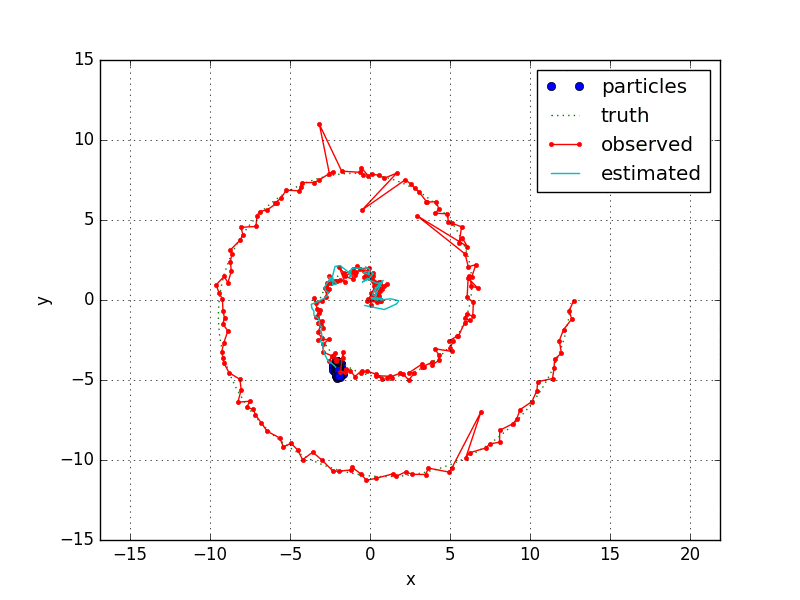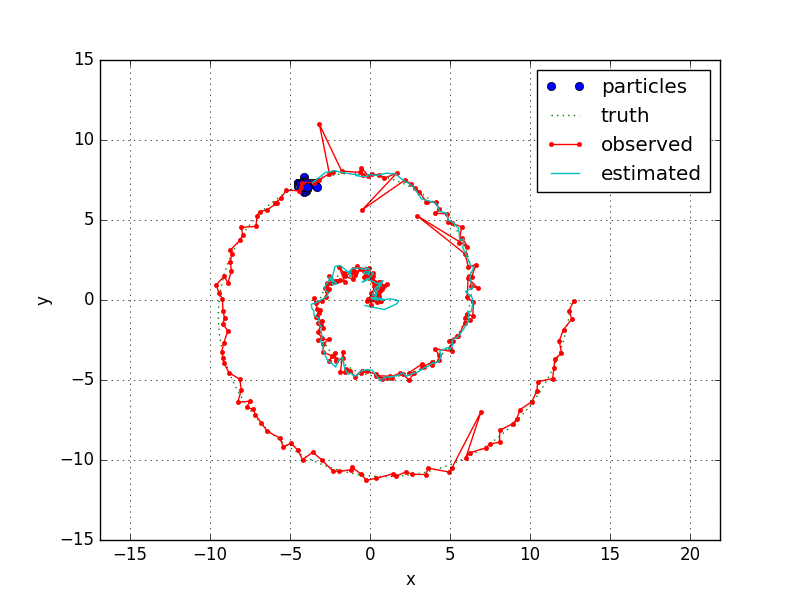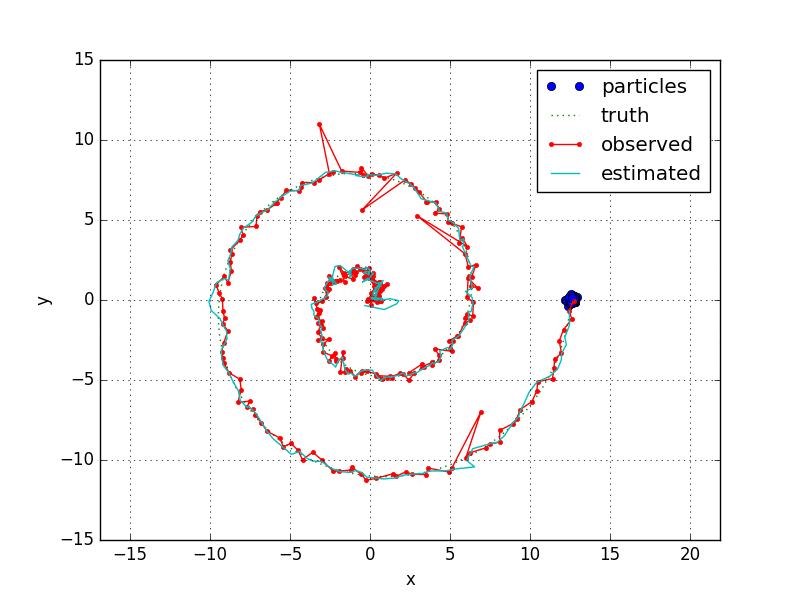
• はじめロックするまでは変なところをウロウロしてます。
• 何点かわざと外れ値を入れていますが、きちんとフィルタリングしているようです。

こここうした方がいいよとか間違ってね？とかあったら気軽にコメントください。
あと、よくわかんないから教えてとかでも歓迎します。

2016/12/14 修正

• ソースがごちゃごちゃしていたのを書き直し。割りとスッキリかけた気がする
• numpyをforで回すと遅いらしいので、リサンプリングをcythonで書き直してみた（あまり変わらず）
• cupyで動かそうとしたが、案の定うまくインストールできず無事死亡（そもそもNVIDIA製のGPUじゃなくてCUDAが動かなかったみたいです。残念）
• カルマンフィルタをおまけで追加

ソース概要

粒子フィルタ

• particle.py
• test_particle.py
• resample.pyx
• utils.py

カルマンフィルタ（おまけ）

• kalman.py
• test_kalman.py

ソースコード

粒子フィルタ本体

• 重み更新時の尤度計算は、対数尤度の和をとってからexpに戻してます。これは、指数の積とったときにオーバーフローが起きるのを防ぐため。
• リサンプリングは、まずインデックスのリストidxsを生成して、pars[:, idxs]とかで一気に撒き直してます。

particle.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-

"""粒子フィルタのpython実装
"""

import pyximport
pyximport.install()
import resample
import numpy as xp
# import cupy as xp


class GaussianNoiseModel(object):
    """多次元ガウス分布
    """

    def __init__(self, Cov):
        """コンストラクタ

        @param ndarray(n,n) Cov : 分散共分散行列
        """
        self._Cov = Cov

    def generate(self, num):
        """ノイズの生成

        @param  int num : 粒子数
        @return ndarray(n,num) : 雑音行列
        """
        n, _ = self._Cov.shape
        return xp.random.multivariate_normal(xp.zeros(n), self._Cov, num).T

    def logpdf(self, X):
        """対数確率密度関数

        @param  ndarray(n,num) X
        @param  int num : 粒子数
        @return ndarray(num) : 対数確率密度
        """
        Cov = self._Cov
        k, _ = Cov.shape
        det_Cov = xp.linalg.det(Cov)
        Cov_inv = xp.linalg.inv(Cov)
        coefs = xp.array([ x.dot(Cov_inv).dot(x.T) for x in X.T ])
        return -k*xp.log(2.*xp.pi)/2. -xp.log(det_Cov)/2. -coefs/2.


class CauchyNoiseModel(object):
    """多次元独立コーシー分布

    各変数に独立を仮定した多次元コーシー分布
    """

    def __init__(self, gma):
        """コンストラクタ

        @param ndarray(n) gma : 尺度母数
        """
        self._gma = gma

    def generate(self, num):
        gma = self._gma
        uni = xp.random.rand(gma.size, num)
        Gma = gma.reshape(gma.size,1) * xp.ones(num)
        return xp.arctan(uni / Gma) /xp.pi + 1./2.

    def logpdf(self, X):
        _, num = X.shape
        gma = self._gma
        Gma = gma.reshape(gma.size,1) * xp.ones(num)
        return xp.sum(xp.log(Gma/xp.pi) - xp.log(X**2 + Gma**2), axis=0)


def _normalize(w):
    """重みの正規化

    @param  ndarray(num) w : 各粒子の重み
    @return ndarray(num) : 各粒子の正規化された重み
    """
    return w / xp.sum(w)


class ParticleFilter(object):
    """Particle Filter (粒子フィルタ)
    """

    def __init__(self, f, g, h, t_noise, o_noise, pars_init):
        """コンストラクタ

        @param ndarray(nx,num) function( ndarray(nx,num) ) f : 状態遷移関数
        @param ndarray(nx,num) function( ndarray(nu,num) ) g : 入力伝搬関数
        @param ndarray(ny,num) function( ndarray(nx,num) ) h : 観測関数
        @param NoiseModel t_noise : システムノイズモデル
        @param NoiseModel o_noise : 観測ノイズモデル
        @param ndarray(nx,num)  pars_init : 粒子の初期値
        """
        self._f = f
        self._g = g
        self._h = h

        self._t_noise = t_noise
        self._o_noise = o_noise

        _, num = pars_init.shape
        self._num = num
        self._w = _normalize(xp.ones(num))
        self._pars = pars_init

    def update(self, y, u):
        """フィルタ更新

        @param ndarray(ny) y : nでの観測ベクトル
        @param ndarray(nu) u : nでの入力ベクトル
        """
        self._update_pars(u)
        self._update_weights(y)
        self._resample()

    def _update_pars(self, u):
        """状態遷移モデルに沿って粒子を更新

        - 状態方程式
            x_n = f(x_n-1) + g(u_n-1) + w
        - 状態ベクトル x_n
        - 入力ベクトル u_n
        - 状態遷移関数 f(x)
        - 入力伝搬関数 g(u)
        - システムノイズ w

        @param  ndarray(nu) u : n-1での入力ベクトル (u_n-1)
        """
        U = u.reshape(u.size,1) * xp.ones(self._num)
        self._pars = self._f(self._pars) + self._g(U) + self._t_noise.generate(self._num)

    def _update_weights(self, y):
        """観測モデルに沿って尤度を計算

        - 観測方程式
            y_n = h(x_n) + v
        - 状態ベクトル x_n
        - 観測ベクトル y_n
        - 観測関数 h(x)
        - 観測ノイズ v

        @param  ndarray(ny) y : nでの観測ベクトル (y_n)
        """
        Y = y.reshape(y.size,1) * xp.ones(self._num)
        loglh = self._o_noise.logpdf( xp.absolute(Y - self._h(self._pars)) )
        self._w = _normalize( xp.exp( xp.log(self._w) + loglh ) )

    def _resample(self):
        """リサンプリング
        """
        wcum = xp.cumsum(self._w)
        num = self._num

        # idxs = [ i for n in xp.sort(xp.random.rand(num))
        #     for i in range(num) if n <= wcum[i] ]

        # start = 0
        # idxs = [ 0 for i in xrange(num) ]
        # for i, n in enumerate( xp.sort(xp.random.rand(num)) ):
        #     for j in range(start, num):
        #         if n <= wcum[j]:
        #             idxs[i] = start = j
        #             break
        idxs = resample.resample(num, wcum)

        self._pars = self._pars[:,idxs]
        self._w = _normalize(self._w[idxs])

    def estimate(self):
        """状態推定

        @return ndarray(nx) : 状態ベクトルの推定値
        """
        return xp.sum(self._pars * self._w, axis=1)

    def particles(self):
        """粒子

        @return ndarray(nx,num)
        """
        return self._pars

リサンプリングはCythonで

ここはちょっと工夫しました。以下のようにすれば、２重のループになっていますが、ほぼ１重ループ分の処理で済みます。ループ回数が粒子数の２乗でなく1乗に比例するので、粒子数を大きくしていったときに速度に大きく差が出ます。

• $[0, 1]$の一様乱数$n_i$を生成して昇順にソートしておく
• 乱数$n_i$を取る
  • 累積重み$w_j$を取る
    • 乱数$n_i$が取った累積重み$w_j$より大きい場合は、次の重み$w_{j+1}$に移る
    • 小さい場合は、そのインデックス$j$を採用 -> 次の乱数$n_{i+1}$に移る
    • ことのき、次の乱数$n_{i+1}$は、$w_{j-1}<n_i<n_{i+1}$なので、$w_j$との比較から始めれば良い

resample.pyx

# -*- coding: utf-8 -*-
#cython: boundscheck=False
#cython: wraparound=False

import numpy as xp
cimport numpy as xp
cimport cython

ctypedef xp.float64_t DOUBLE_t
ctypedef xp.int_t INT_t

def resample(int num, xp.ndarray[DOUBLE_t, ndim=1] wcum):
    cdef int start, i, j, length
    cdef double n

    start = 0
    cdef xp.ndarray[INT_t, ndim=1] idxs = xp.zeros(num).astype(xp.int)
    cdef xp.ndarray[DOUBLE_t, ndim=1] rand = xp.sort(xp.random.rand(num))
    length = rand.size

    for i in xrange(length):
        for j in xrange(start, num):
            if rand[i] <= wcum[j]:
                idxs[i] = start = j
                break

    return idxs

resample_setup.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-
#filename_setup.py
from distutils.core import setup
from distutils.extension import Extension
from Cython.Distutils import build_ext as build_pyx
import numpy

setup(
    name = 'resample',
    ext_modules = [Extension('resample', ['resample.pyx'])],
    cmdclass = { 'build_ext': build_pyx },
    include_dirs = [numpy.get_include()],
)

$ cython -a resample.pyx # コンパイル
$ python resample_setup.py build_ext --inplace # ビルド

Cythonよくわかってないせいか、あんまり早くなりませんでした。
（詳しい方コメントいただけるとありがたいです）

利用プログラムサンプル

システムノイズ、観測ノイズを多次元の独立コーシー分布とした場合。はずれ値耐性がつく。
参考：自己組織化型状態空間モデルを用いた運動軌跡のフィルタリング

py.test_particle.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-

"""particle.pyの利用サンプル
"""

import particle as par
import utils
import numpy as xp
# import cupy as xp


# パラメータ設定 --------------------
num = 3000  # 粒子数
v_sys = 0.01  # システムノイズの共分散
v_obs = 0.1  # 観測ノイズの共分散
v_noise = 0.05

# 初期粒子
mins = -5. * xp.ones(4)
maxs = +5. * xp.ones(4)
pars_init = utils.rand_uniform(mins, maxs, num)
# ---------------------------------

dataset = utils.load_data("testdata")
# dataset = utils.generate_data("testdata")

# 状態モデルの生成 (2次階差モデル)
A = xp.kron(xp.eye(2), xp.array([[2, -1], [1, 0]]))
f = lambda X: A.dot(X)  # 状態遷移関数の定義
B = xp.zeros(1)
g = lambda U: B.dot(U)

C = xp.ones(4) * v_sys
sysn_model = par.CauchyNoiseModel(C)

# 観測モデルの生成 (直接観測モデル)
D = xp.kron(xp.eye(2), xp.array([1, 0]))
h = lambda X: D.dot(X)  # 観測関数の定義

E = xp.ones(2) * v_obs
obsn_model = par.CauchyNoiseModel(E)

# 初期プロット
lines = utils.init_plot_particle(dataset, pars_init)

# 粒子フィルタの生成
pf = par.ParticleFilter(
    f, g, h, sysn_model, obsn_model, pars_init)

x_est = xp.zeros(dataset.x.shape)
for i, y in enumerate(dataset.y):
    pf.update(y, xp.zeros(1))
    state = pf.estimate()
    x_est[i,:] = h(state)

    # データのプロット
    pars = pf.particles()
    utils.plot_each_particle(lines, x_est, pars, i)

# utils.save_as_gif_particle(dataset, pars_init, pf, "particle_selforganized.gif")

プロットとかutility系

utiils.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-


import matplotlib.animation as animation
import matplotlib.pyplot as plt
from collections import namedtuple
import numpy as xp
# import cupy as xp


Dataset = namedtuple("Dataset", ["t", "x", "y"])


def load_data(dirname):
    t = xp.loadtxt(dirname + "/t.txt")
    x = xp.loadtxt(dirname + "/x.txt")
    y = xp.loadtxt(dirname + "/y.txt")
    dataset = Dataset(t=t, x=x, y=y)
    return dataset


def save_data(dirname, dataset):
    xp.savetxt(dirname + "/t.txt", dataset.t)
    xp.savetxt(dirname + "/x.txt", dataset.x)
    xp.savetxt(dirname + "/y.txt", dataset.y)


def generate_data(dirname):
    # truth
    t = xp.arange(0, 6*xp.pi, 0.05)
    x = xp.c_[t*xp.cos(t), t*xp.sin(t)]

    # noise
    nr, nc = x.shape
    idx = xp.random.randint(nr/2, nr, 5)
    n = xp.random.normal(0., xp.sqrt(v_noise), x.shape)
    n[nr/3:2*nr/3,:] = xp.random.normal(0., xp.sqrt(v_noise*10), (2*nr/3-nr/3,nc))
    n[idx,:] += xp.random.normal(0., xp.sqrt(v_noise)*20, (5,nc))

    # observation
    y = x + n
    x_est = xp.zeros(x.shape)
    Dataset = namedtuple("Dataset", ["t", "x", "y"])
    dataset = Dataset(t=t, x=x, y=y)

    save_data(dirname, dataset)
    return dataset


def init_plot_particle(dataset, pars):
    fig, ax = plt.subplots(1, 1)
    ax.hold(True)
    ax.axis("equal")
    lines = []
    lines.append( ax.plot(pars[0,:], pars[2,:], "o") )
    lines.append( ax.plot(dataset.x.T[0], dataset.x.T[1], ":"))
    lines.append( ax.plot(dataset.y.T[0], dataset.y.T[1], ".-"))
    lines.append( ax.plot([0], [0]) )
    plt.legend(["particles", "truth", "observed", "estimated"])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.grid(True)
    return lines


def plot_each_particle(lines, x_est, pars, i):
    lines[0][0].set_data(pars[0,:], pars[2,:])
    lines[3][0].set_data(x_est.T[0][:i], x_est.T[1][:i])
    plt.pause(1e-5)


def save_as_gif_particle(dataset, pars_init, pf, filename):
    x_est = xp.zeros(dataset.x.shape)
    lines = init_plot_particle(dataset, pars_init, x_est)

    def draw(i):
        pf.update(dataset.y[i])
        state = pf.estimate()
        x_est[i,:] = [state[0], state[2]]

        # データのプロット
        pars = pf.particles()
        plot_each_particle(lines, x_est, pars, i)

    ny, _ = dataset.y.shape
    ani = animation.FuncAnimation(fig, draw, ny, blit=False, interval=100, repeat=False)
    ani.save(filename, writer="imagemagick")


def init_plot_kalman(dataset):
    fig, ax = plt.subplots(1, 1)
    ax.hold(True)
    ax.axis("equal")
    lines = []
    lines.append( ax.plot(dataset.x.T[0], dataset.x.T[1], ":"))
    lines.append( ax.plot(dataset.y.T[0], dataset.y.T[1], ".-"))
    lines.append( ax.plot([0], [0]) )
    plt.legend(["truth", "observed", "estimated"])
    plt.xlabel("x")
    plt.ylabel("y")
    plt.grid(True)
    return lines


def plot_each_kalman(lines, x_est, i):
    lines[2][0].set_data(x_est.T[0][:i], x_est.T[1][:i])
    plt.pause(1e-5)


def save_as_gif_kalman(dataset, kf, filename):
    x_est = xp.zeros(dataset.x.shape)
    lines = init_plot_kalman(dataset, x_est)

    def draw(i):
        kf.update(dataset.y[i])
        state = pf.estimate()
        x_est[i,:] = [state[0], state[2]]

        # データのプロット
        plot_each_kalman(lines, x_est, i)

    ny, _ = dataset.y.shape
    ani = animation.FuncAnimation(fig, draw, ny, blit=False, interval=100, repeat=False)
    ani.save(filename, writer="imagemagick")


def rand_uniform(mins, maxs, num):
    """初期粒子の生成用

    @param  ndarray(nx) mins : 粒子の各最小値
    @param  ndarray(nx) maxs : 粒子の各最大値
    @param  int num : 粒子数
    @return ndarray(nx,num)  : 初期粒子
    """
    nx = mins.size
    return (mins.reshape(nx, 1) * xp.ones(num)
        + (maxs - mins).reshape(nx, 1) * xp.random.rand(nx, num))

おまけ

カルマンフィルタ本体

kalman.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-

"""カルマンフィルタのpython実装
"""

import numpy as xp
# import cupy as xp


class KalmanFilter(object):

    def __init__(self, F, H, Q, R, x_init, P_init):
        self._x = x_init.reshape(-1,1)
        self._P = P_init

        self._update_x    = lambda x     : F.dot(x)
        self._update_P    = lambda P     : Q + F.dot(P).dot(F.T)
        self._error       = lambda x,y   : y - H.dot(x)
        self._cov_P       = lambda P     : R + H.dot(P).dot(H.T)
        self._kalman_gain = lambda P,S   : P.dot(H.T).dot(xp.linalg.inv(S))
        self._estimate_x  = lambda x,K,e : x + K.dot(e)
        self._estimate_P  = lambda P,K   : (xp.eye(*P.shape)-K.dot(H)).dot(P)

    def update(self, y):
        # 予測
        x_predicted = self._update_x(self._x)
        P_predicted = self._update_P(self._P)

        # パラメータ計算
        e = self._error(x_predicted, y.reshape(-1,1))
        S = self._cov_P(P_predicted)
        K = self._kalman_gain(P_predicted, S)

        # 更新
        self._x = self._estimate_x(x_predicted, K, e)
        self._P = self._estimate_P(P_predicted, K)

    def estimate(self):
        return self._x

利用プログラムサンプル

test_kalman.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-

"""kalman.pyの利用サンプル
"""

import kalman
import utils
import numpy as xp
# import cupy as xp


# パラメータ設定 --------------------
var_Q = 0.01
var_R = 1

x_init = xp.zeros(4)
P_init = xp.ones(4)
# ---------------------------------

dataset = utils.load_data("testdata")
# dataset = utils.generate_data("testdata")

# 状態モデルの生成 (2次階差モデル)
F = xp.kron(xp.eye(2), xp.array([[2, -1], [1, 0]]))
Q = var_Q * xp.eye(4)

# 観測モデルの生成 (直接観測モデル)
H = xp.kron(xp.eye(2), xp.array([1, 0]))
R = var_R * xp.eye(2)

# 初期プロット
lines = utils.init_plot_kalman(dataset)

kf = kalman.KalmanFilter(F, H, Q, R, x_init, P_init)

x_est = xp.zeros(dataset.x.shape)
for i, y in enumerate(dataset.y):
    kf.update(y)
    state = kf.estimate()
    x_est[i,:] = H.dot(state.reshape(-1,1)).T

    # データのプロット
    utils.plot_each_kalman(lines, x_est, i)

# utils.save_as_gif_kalman(dataset, kf, "kalman.gif")