はじめに
Tensorflow probability(以降、TFPという)はTensorflow 1.12から公式サポートにされることになった確率的プログラミングのモジュールです。これを使うことでtensorflow上でMCMCを用いたモデル化が可能となり、より多彩なモデリングができそうな予感がします。
私自身は、またベイズ推計そのものが研究中ということもあり、Stanをベースにモデリングをしています。とはいえ、せっかくtensorflowを使えるのだから触っておいて損はないだろうということで、最近、ネットで参考になるコードを読むという取り組みを始めました。
ところが、これがなかなかの歯ごたえです。そもそもベイズ推定はニューラルネットワークよりも必要とされる数学的知識の幅が広いためハードル高めです。それに加えて先行している方々のコードを見るとこれまで使ってきたニューラルネットワーク(CNN含む)とは似つかない部分が多く別世界のようです。
そこで本論は、ニューラルネットワークの実装経験があり、次のステップとしてTFPを考えている人に向けてこれまで調べてきたことをもとに実装の解説をしようと思います。解説には、ニューラルネットワークをベースモデルとして実装し、これを発射台に改造を加えながらMCMCへと移行していきます。こうすることで、これまでに理解してきたニューラルネットワークとMCMCの実装上の相違点やニューラルネットワークにおけるコスト関数がMCMCでは何に当たるのかなどが感覚的に理解できるようにしたいと思います。
また、適宜、stanのコードも加えます。これによりstanとの相違もつかめるようにしたいと思います。
環境について
本論は以下の環境で実装しています。
OS:windows10
puthon: 3.7.6
tensorflow 1.15.0
tensorflow-probability: 0.8.0
pystan:2.19
tensorflowはすでに2.0系が公開されていますが、当方はフォローしていないため、少し古いバージョンとなっています。2系になって1系とかなりAPIの仕様が変更になったようなので、適宜修正ください。
また、tfpもtensorflowのバージョン依存するため、バージョン古めです。公式HPによると開発途上なのでAPI仕様がいろいろ変わるということなので、本論記載のコードがそのまま稼働するわけではないことを了解願います。
単回帰
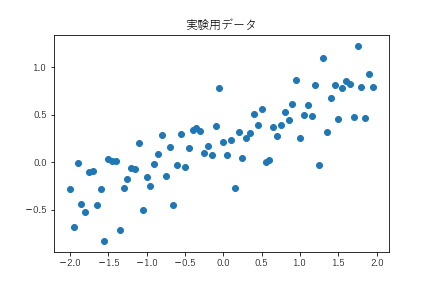
問題の設定は以下とします。
X_train = np.arange(-2,2,0.05)
Y_train = X_train * 0.3 +0.2 + stats.norm.rvs(loc=0,scale=0.25,size=len(X_train),random_state=1234)
X_train = X_train.reshape(-1,1)
Y_train = Y_train.reshape(-1,1)
最小二乗法
ニューラルネットで最小二乗法によるモデル化を図ります。これがベースラインとなり、以後、このコードを改良していきます。
features = tf.placeholder(dtype=tf.float32,shape=[None,1])
target = tf.placeholder(dtype=tf.float32,shape=[None,1])
weight = tf.Variable(tf.truncated_normal([1,1]))
bias = tf.Variable(tf.zeros([1]))
def linear_regression(features) :
linear_predictor = tf.matmul(features,weight) + bias
return linear_predictor
p = linear_regression(features)
cost = tf.reduce_mean((p-target)**2)
train = tf.train.AdamOptimizer().minimize(cost)
| パラメータ | 値 |
|---|---|
| weight | 0.3047776 |
| bias | 0.2144405 |
推計結果は上記となりました。
最尤推計
上記からMCMCに向けて改良するのですが、少しジャンプが激しいので一度最尤推計をはさみたいと思います。
最尤推計とは何かですが、実装の違いに着目して解説します。最尤推計が最小二乗法と違う点はコスト関数にあります。最小二乗法の場合、コストは予測値と観測値の差異を用います。これは予測値と観測値の差異はモデルの性能に問題があるため生じているというとらえ方をしていることによるものです。
一方、最尤推計の場合、予測値と観測値の差異をモデルの性能の問題とはみなさず、偶発的な要因によって生じる誤差ととらえます。その上でこの誤差が何らかの確率分布に従って発生すると考えます。この確率分布はモデル構築者が任意に決定できるのですが、ここでは正規分布に従うものとしておきます。つまり、観測値は、本来、予測値(weight × feature + bias)が出現するはずであるが、予測値を平均とした正規分布にしたがってランダムに出力されると考えます。この誤差を発生させるメカニズムを確率分布(ここでは正規分布)を使って定義することで、観測値がこの正規分布から出現する可能性を計算することができます。これを尤度といいます。尤度は、予測値と観測値が近似すれば大きくなります。また、予測値と観測値が多少異なっても標準偏差が大きくなると尤度は大きくなります。よってこの尤度をコスト関数として定義することで、予測値を決定するweight・bias、誤差のバラつきを決定する標準偏差をoptimizerによって最適化すれば必要なモデルパラメータが手に入ることになります。
それでは実際のコードの解説をします。
features = tf.placeholder(dtype=tf.float32,shape=[None,1])
target = tf.placeholder(dtype=tf.float32,shape=[None,1])
weight = tf.Variable(tf.truncated_normal([1,1]))
bias = tf.Variable(tf.zeros([1]))
sigma = tf.Variable(tf.ones([1]))
def linear_regression(features) :
mu = tf.matmul(features,weight) + bias
return tfp.edward2.Normal(loc=mu, scale=sigma,name='observed')
p = linear_regression(features)
log_joint = tfp.edward2.make_log_joint_fn(linear_regression)
cost = -log_joint(features,observed=target)
train = tf.train.AdamOptimizer().minimize(cost)
まず、学習対象の変数としてsigmaを追加しています。先に述べたとおり、最尤推定は予測値と観測値の差異は正規分布に従って決定されます。正規分布には平均と標準偏差がパラメータとして必要となります。平均はwightとbiasによって計算されるものなので標準偏差をsigmaとして定義する必要があります。
次にlinear_regression()を改修します。先に述べたとおり、最尤推定のモデルの出力値は予測値に誤差を加えたものなので。これを実装します。具体的にはtfp.edward2.Normal()を用いています。tfp.edward2の直下には様々な確率分布が実装されているので、誤差を発生される統計分布に分布に応じてNormalやPoissonなどを用います。
続いて尤度の計算とそのコスト化を実装します。まず、定義したモデル(linear_regression)から尤度の計算する関数を生成する関数をlog_jointとして定義します。このlog_jointはモデルの引数であるfeatureとその計算結果と観測値であるtargetを引数として与えることで尤度が計算されるます。尤度は上に凸の関数なので、optimaizerを適用するためにマイナス記号を付けて正負を反転させています。
学習結果は以下となりました。
| パラメータ | 真値 | 最小二乗法 | 最尤推定 |
|---|---|---|---|
| weight | 0.30 | 0.3047776 | 0.30411524 |
| bias | 0.20 | 0.2144405 | 0.21442308 |
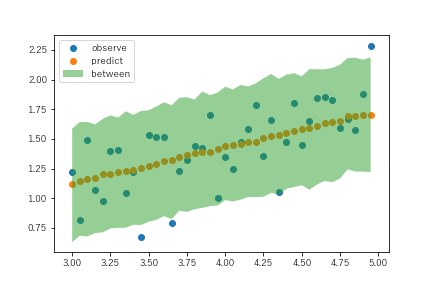
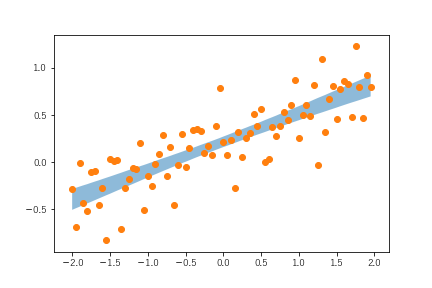
単にパラメータを推計するだけであれば最小二乗法ベースも最尤推計ベースも大差ありません。最尤推計ベースの場合、予測値の取りうる範囲を推計することができます。実装のlinear_regressionは最後に正規分布に従った誤差を加えています。よって学習後のモデルを使って予測をすると、実行するたびに結果が異なります。そこで、予測を1000回実施し、同じfeatureが1000個入手されたときに観測されうるtargetを1000個計算します。
もともと、linear_regressionの戻り値はreturn tfp.edward2.Normal(loc=mu, scale=sigma,name='observed')として定義されているように戻り値の平均はモデルの計算結果(mu)そのものなので、1000個の平均は予測結果そのものに近似します。加えて1000個の計算結果は正規分布に近似したものになるので、これを活用することで、観測値の取りうる範囲を推計することができます。
実装と結果を以下に示します。
X_test = np.arange(3,5,0.05)
Y_test = X_test * 0.3 +0.2 + stats.norm.rvs(loc=0,scale=0.25,size=len(X_test),random_state=1234)
X_test = X_test.reshape(-1,1)
Y_test = Y_test.reshape(-1,1)
predict_df = pd.DataFrame([])
for i in range(1000) :
tmp = pd.DataFrame(sess.run(p,feed_dict={features:X_test}),columns=[i])
predict_df = pd.concat([predict_df,tmp],axis=1)
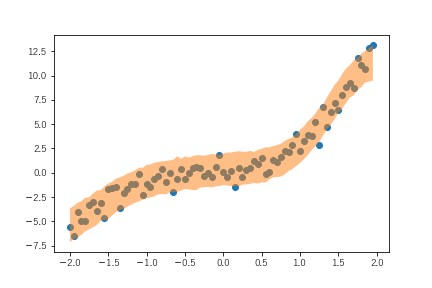
plt.scatter(X_test,Y_test,label='')
plt.scatter(X_test,predict_df.mean(axis=1))
Between = stats.mstats.mquantiles(predict_df,axis=1,prob=[0.025,0.975])
plt.fill_between(x=X_test.flatten(),y1=Between[:,0],y2=Between[:,1],alpha=0.5)
plt.show()
betweenが予測結果の観測される範囲です。ただし、これはあくまでも1000回の試行の結果より上下の2.5%分をカットしたものなので、統計でいうところの区間推計とは異なります。とはいえ、テストデータについても予測結果と観測値の乖離は偶発的な要因によって説明できることが、観測値の大部分が推計範囲に収まっていることからわかります。別の言い方をすると、この範囲推計から外れたテストデータの観測値が多いようであれば、モデルの見直しなどを考えたほうがいいということになります。
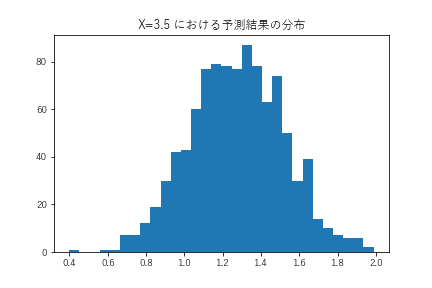
また、特定のインプット一組に対する予測結果は以下のような分布を描きます。
この分布を活用することで、最悪の予測結果の見積もることができます。例えば、商品の販売数を予測し、これをもとに発注数を判断するようなタスクの場合、この分布から最悪時の販売数を前提に発注数を決定することで売れ残りがないようにするという判断もできれば、最良時の販売数を前提に売り逃しがないようにするという判断もできるようになります。
MCMC
最終段階のMCMCに移行します。MCMCも範疇でいえば、最尤推定になるので先の最尤推計のコードをさらに改修していきます。MCMCはベイズ推定がベースになります。このベイズ推定ですが目標は推定対象であるパラメータの分布そのものを推定することにあります。MCMCはそのための計算アルゴリズムであり、そのアルゴリズムを使うために適宜必要なコードの改修を行っていると考えれば全体の理解がわかりやすくなります。
features = tf.placeholder(tf.float32,shape=([None,1]))
target = tf.placeholder(tf.float32,shape=([None,1]))
def linear_regression(features):
weight = tfp.edward2.Normal(loc=tf.zeros([1,1]), scale=100., name="weight")
bias = tfp.edward2.Normal(loc=tf.zeros([1]), scale=100., name="bias")
scale = tfp.edward2.HalfNormal(1, name="scale")
mu = tf.matmul(features,weight) + bias
outcomes = tfp.edward2.Normal(
loc=mu,
scale=scale,
name="outcomes")
return outcomes
log_joint = tfp.edward2.make_log_joint_fn(linear_regression)
def target_log_prob_fn(weight, bias, scale):
return log_joint(features=features,
weight=weight,
bias=bias,
scale=scale,
outcomes=target)
weight_init = tf.get_variable('weight',shape=[1,1])
bias_init = tf.get_variable('bias',shape=[1])
scale_init = tf.get_variable('scale',shape=[1])[0]
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
num_leapfrog_steps=3,
step_size=tf.Variable(0.01),
step_size_update_fn=tfp.mcmc.make_simple_step_size_update_policy(1))
[
[weight, bias, scale],
kernel_results,
] = tfp.mcmc.sample_chain(
num_results=3000,
num_burnin_steps=800,
current_state=[weight_init, bias_init, scale_init],
parallel_iterations=500,
kernel=hmc)
weight_trans = tf.reshape(weight,([1,tf.shape(weight)[0]]))
bias_trans = tf.reshape(bias,([1,tf.shape(bias)[0]]))
p1 = tf.matmul(features,weight_trans)+bias_trans
まず予測対象の変数としての定義をしていません。MCMCは値を予測するというよりも分布を推計するものなので、tf.Variableを使って定義しません。その代わりという言い方は変なのですが、予測対象のパラメータはlinear_regressionのなかで定義します。この際、学習結果をモデルに反映する必要があるので、変数名を定義することで関数の外部からその変数にアクセスできようにします。
尤度の計算ですが、make_log_joint_fnを使って関数にした上でさらにtarget_log_prob_fnという名称でラップしています。こうすることで、weight・bias・sigmaが学習によって更新された結果を使って尤度を計算することを繰り返し行えるようにしています。繰り返し計算には、初期条件の設定が必要です。そこで、linear_regression内で定義した変数にアクセスしてedward2を使ってランダムに生成した変数を取り出して初期値とします。
次にoptimizerに相当するコードを記述します。MCMCの場合、サンプリングと呼ばれる方法論を使用する必要があるので、それを実装する必要があります。サンプリング法には、メトロポリスヘイスティング・ハミルトニアンモンテカルロ法などがあります。ここではハミルトニアンモンテカルロ法を用いています。なお、stanでは標準的に実装されているNUTSUはTFPの場合は最新バージョンでサポートされるようになったようです。
引数のうち必須のものは、target_log_prob_fn,num_leapfrog_steps,step_sizeの3つです。target_log_probは尤度関数の名称、leapfrog_stepsとstep_sizeはoptimizerの学習率あたりに相当するものだと思うのですがまだ理解できていません。設定しているパラメータも参考にしたコードの丸写しです。なお、step_sizeは学習の都度変更されるものにしています。定数でも実行は可能ですが、試した範囲ではコードのようにしたほうがうまくいく印象です。この引数を可変としたため、step_size_update_fnおを指定しています。
最後にニューラルネットでいうiterationに相当するコードを実装します。ニューラルネットの場合、iterationはモデルの外側で実装するイメージでしたが、MCMCの場合はモデルに近い位置づけのようでtensorflow内に実装します。num_resultsがiterationの回数に相当します。num_burnin_stepsはiterationのうち、サンプリングに必要としないステップ数を意味します。MCMCも初期値を出発点に学習されていくので、学習の初期のころは収束していません。この収束前の計算結果を破棄するための引数ということになります。current_stateは初期設定値です。指定の順序は重要で尤度関数の引数の順番と一致させる必要があります。
以上で実装は終わりで、あとはsess.runによって実行するだけです。実行時のiterationは不要ですので注意しましょう。ただし、stanの場合、chain数といった一連の学習処理を複数回実行する引数の指定が可能です。先のsample_chainにはこのchain数に相当するものがないので、この段階で指定してもいいように思います。
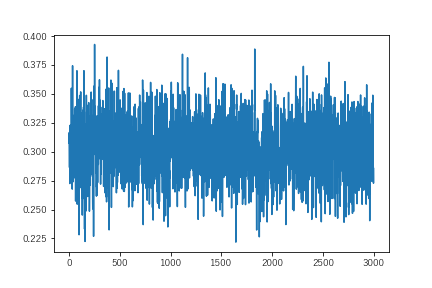
まず、weightの学習結果を確認してみます。
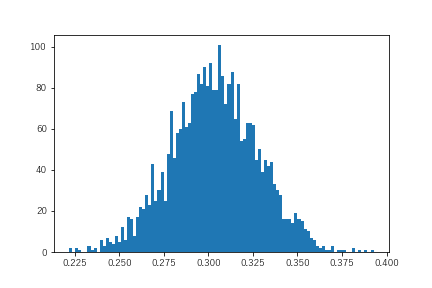
真値を中心に前後しておりうまく学習しています。各値はweightの取りうる値なのでヒストグラムで可視化してみます。
これがweightの取りうる分布ということになります。これを使ってweightの取りうる範囲の推計や平均を計算することでweightの推計値を得ることができます。同様の処理はbiasについても行うことができます。よって、このweightとbiasの組み合わせ(3000回)が得られているので、これを使うことでパラメータのゆらぎを考慮した予測値の取りうる範囲推計も可能です。
実はこのあたりの処理がweight_trans以降の部分なので、この結果を取り出したいと思います。
あくまでの試行の範囲内という条件付きですが、この範囲内がパラメータのゆらぎを考慮した範囲推計ということになります。いいかえると、この範囲内に収まる観測値はパラメータの推計誤差で説明されるものということになります。ニューラルネットなどの際、交差検証を行いますが、この範囲推計がそれに近いものと考えるといいと思います。
重回帰
重回帰への拡張そのものはそれほど難しいものではありません。MCMCのコードを以下に示します。
def linear_regression(features):
weight = tfp.edward2.Normal(loc=tf.zeros([2,1]), scale=100., name="weight")
bias = tfp.edward2.Normal(loc=tf.zeros([1]), scale=100., name="bias")
scale = tfp.edward2.HalfNormal(1, name="scale")
mu = tf.matmul(features,weight) + bias
outcomes = tfp.edward2.Normal(
loc=mu,
scale=scale,
name="outcomes")
return outcomes
log_joint = tfp.edward2.make_log_joint_fn(linear_regression)
features = tf.placeholder(tf.float32,shape=([None,2]))
target = tf.placeholder(tf.float32,shape=([None,1]))
def target_log_prob_fn(weight, bias, scale):
return log_joint(features=features,
weight=weight,
bias=bias,
scale=scale,
outcomes=target)
weight_init = tf.get_variable('weight',shape=[2,1])
bias_init = tf.get_variable('bias',shape=[1])
scale_init = tf.get_variable('scale',shape=[1])[0]
log_prob = target_log_prob_fn(weight_init,bias_init,scale_init)
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
num_leapfrog_steps=3,
step_size=tf.Variable(0.01),
step_size_update_fn=tfp.mcmc.make_simple_step_size_update_policy(1))
[
[weight, bias, scale],
kernel_results,
] = tfp.mcmc.sample_chain(
num_results=3000,
num_burnin_steps=800,
current_state=[weight_init, bias_init, scale_init],
parallel_iterations=500,
kernel=hmc)
先のモデルとの大きな相違点はlinear_regressionのweightの形状です。その結果、初期値を取り出すコードが変更になっています。学習結果のパラメータの動きは収束傾向を示すので、これで学習できることと言っていいでしょう。
隠れ層のあるニューラルネットワーク
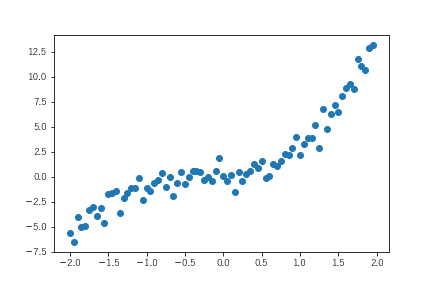
次の段階としてニューラルネットワークを実装します。問題の設定は以下とします。
データは3次関数から生成していますが、分析者はそのことがわからないという設定です。モデルが高次関数であることがわからないのでニューラルネットワークで表現します。
ニューラルネットワーク
コードは以下です。隠れ層を1つ加えたモデルとしています。なお、隠れ層に対する信号の伝達の際には、sigmoid関数を挟んでいます。こうすることで、xの値が特定値より大きいかどうかで信号の強弱をコントロールしてうまく学習できるようにしました。
features = tf.placeholder(dtype=tf.float32,shape=[None,1])
target = tf.placeholder(dtype=tf.float32,shape=[None,1])
weight1 = tf.Variable(tf.truncated_normal([1,5]))
bias1 = tf.Variable(tf.zeros([5]))
weight2 = tf.Variable(tf.truncated_normal([5,1]))
bias2 = tf.Variable(tf.zeros([1]))
def linear_regression(features) :
p1 = tf.sigmoid(tf.matmul(features,weight1) + bias1)
p2 = tf.matmul(p1,weight2) + bias2
return p2
p = linear_regression(features)
cost = tf.reduce_mean((p-target)**2)
train = tf.train.AdamOptimizer().minimize(cost)
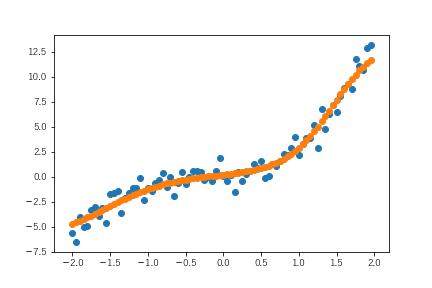
この結果をベースラインとします。
最尤推計
最尤推計への改良はlinear_regressionを行うだけです。ここでは、結果だけを示しておきます。
MCMC
続いてMCMCに移行します。実装方針はこれまでの回帰のケースと同じです。
def linear_regression(features):
weight1 = tfp.edward2.Normal(loc=tf.zeros([1,5]),
scale=10,
name="weight1")
bias1 = tfp.edward2.Normal(loc=tf.zeros([5]),
scale=10,
name="bias1")
weight2 = tfp.edward2.Normal(loc=tf.zeros([5,1]), scale=10., name="weight2")
bias2 = tfp.edward2.Normal(loc=tf.zeros([1]), scale=10., name="bias2")
scale = tfp.trainable_distributions.softplus_and_shift(tfp.edward2.HalfNormal(scale=10, name="scale"))
p1 = tf.sigmoid(tf.matmul(features,weight1) + bias1)
p2 = tf.matmul(p1,weight2) + bias2
outcomes = tfp.edward2.Normal(
loc=p2,
scale=scale,
name="outcomes")
return outcomes
log_joint = tfp.edward2.make_log_joint_fn(linear_regression)
features = tf.placeholder(tf.float32,shape=([None,1]))
outcomes_true = tf.placeholder(tf.float32,shape=([None,1]))
def target_log_prob_fn(weight1, bias1, weight2, bias2,scale):
## def target_log_prob_fn(weight2, bias2,scale):
return log_joint(features=features,
weight1=weight1,
bias1=bias1,
weight2=weight2,
bias2=bias2,
scale=scale,
outcomes=outcomes_true)
weight_init1 = tf.get_variable('weight1',shape=[1,5])
bias_init1 = tf.get_variable('bias1',shape=[5,])
weight_init2 = tf.get_variable('weight2',shape=[5,1])
bias_init2 = tf.get_variable('bias2',shape=[1,])
scale_init = tf.get_variable('scale',shape=[1,])[0]
## weight_init = tfp.edward2.Normal(loc=[0.], scale=100.)
## bias_init = tfp.edward2.Normal(loc=0., scale=100.)
## scale_init = tfp.edward2.HalfNormal(scale=5.)
hmc = tfp.mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
num_leapfrog_steps=70,
step_size=tf.Variable(0.01),
state_gradients_are_stopped=True,
step_size_update_fn=tfp.mcmc.make_simple_step_size_update_policy(1))
[
[weight1, bias1, weight2,bias2,scale],
## [weight2,bias2,scale],
kernel_results,
] = tfp.mcmc.sample_chain(
num_results=5000,
num_burnin_steps=1000,
current_state=[weight_init1, bias_init1,weight_init2, bias_init2, scale_init],
## current_state=[weight_init2, bias_init2, scale_init],
parallel_iterations=4,
kernel=hmc)
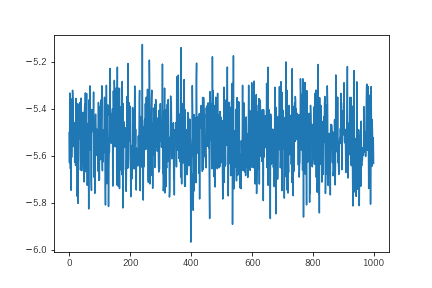
学習させましたが、パラメータが思ったよりうまく収束しません。パラメータのひとつについてサンプリングの推移を示します。
先ほどの単回帰のケースと比較すると明らかに学習結果があちこちに飛び回っています。MCMCの特性上、推計値を平均にうまく前後するべきものなのでもう少し工夫が必要そうです。stanでいうところの事前分布に相当するtfp.edward2.Normalの部分に手を入れることで結果が安定すると思います。このあたりがニューラルネットワークや最尤推定よりも使いこなすことが難しい点と思います。
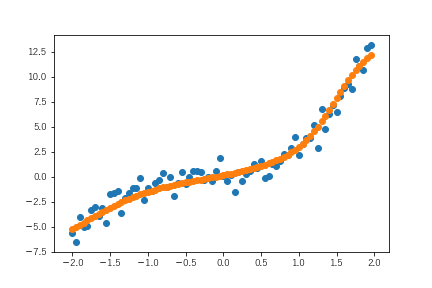
ただ、予測結果は以下のようになり、パラメータの不安定性の割にモデルは観測値をうまく表現しています。
ちなみにstanで以下のモデルを使ってサンプリングしたのですが、同じようにパラメータの安定性が得られませんでした。
data {
int N ;
real x[N] ;
real y[N] ;
}
parameters {
vector[5] weight1 ;
vector[5] bias1 ;
vector[5] weight2 ;
real bias2 ;
real<lower=0> sigma ;
}
model {
vector[5] p1 ;
for (i in 1:N) {
p1 = inv_logit(x[i]*weight1 + bias1) ;
y[i] ~ normal(dot_product(p1,weight2) + bias2 , sigma) ;
}
}
generated quantities {
real predict[N] ;
for (j in 1:N) {
predict[j] = normal_rng(dot_product(inv_logit(x[j]*weight1 + bias1),weight2) + bias2 , sigma) ;
}
}
これから、階層を重ねるモデルの場合、パラメータの事前分布をうまく設定しないとサンプリングがうまくいかないようです。よって、TFPのモデルについても事前分布を調整しないとパラメータの分布は安定しないことがわかります。サンプリングだとうまくいかなかったので、上記のstanのコードをもとに変分ベイズを行います。pystanのバージョン2.19には変分ベイズが実装されているのでこれを使って学習させます。
result = model.vb(data=stan_data,seed=1234567890)
post_dist = pd.DataFrame(result['sampler_params'],index=result['sampler_param_names'])
tmp = post_dist.iloc[17:-1,:].values
MEANS = np.mean(tmp,axis=1)
between95 = stats.mstats.mquantiles(tmp,[0.025,0.975],axis=1)
plt.scatter(X_train.flatten(),MEANS)
plt.scatter(X_train,Y_train2)
plt.fill_between(x=X_train.flatten(),y1=between95[:,0],y2=between95[:,1],alpha=0.5)
plt.show()
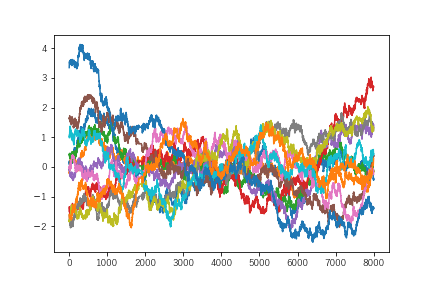
パラメータの変化を以下に示します。
先のものと比較するとパラメータの安定性は明らかに違います。ニューラルネットワークのような複雑なモデルの場合、サンプリングよりも変分ベイズのほうがうまくいきやすいのかもしれません。
しかしながら、tfpで変分ベイズの実装が見当たりません。以下に例示がありましたが、ゴリゴリにtensorflowで実装しています。確かに理論をそのままtensoflowのローレイヤの関数を用いて実装すれば実現可能なのかもしれませんが、一般的なユーザでは検証が極めて困難です。そういう意味でも、もう少しこなれた関数を用いて実装できるようにならないと厳しいように思われます。まだTFPは開発中といわれているので今後のバージョンアップに期待したいと思います。
他クラス分類
回帰についで実装することの多い分類についての解説です。こちらについても通常のニューラルネットワークから始めて徐々に改良してきます。
題材としては、scikitlearnにあるIRISを使用します。
ニューラルネットワーク(ロジスティックモデル)
まずは、ベースモデルとしてニューラルネットワークを実装します。といっても隠れ層を持たないモデルとするので実質的にはロジスティックモデルと相違ありません。実装は以下とします。
features = tf.placeholder(dtype=tf.float32,shape=[None,4])
target = tf.placeholder(dtype=tf.float32,shape=[None,3])
weight = tf.Variable(tf.truncated_normal([4,3]))
bias = tf.Variable(tf.zeros([3]))
def logistic_model(x) :
p = tf.nn.softmax(tf.matmul(x,weight) + bias )
return p
prob = logistic_model(features)
cost = -tf.reduce_mean(tf.log(prob)*target)
train = tf.train.AdamOptimizer().minimize(cost)
最尤推定
回帰と同じでコスト関数の考え方が異なります。ニューラルネットワークは予測結果を各クラスに属する確率としていることもあり、その確率を正解との差異をエントロピーとして評価し、コストに換算します。一方、最尤推定の場合は、尤度を使ってコスト関数を定義します。尤度を計算するためには観測値を出力する確率分布を定義する必要があります。今回の多クラス分類には多項分布を用います。
多項分布は、例としていうと、出目の確率が異なるサイコロを同時に複数個振ったときの目の比率を表す確率分布です。この試行回数を1回とするとIRISのような多クラスの出現を表す確率分布となります。あとは、この確率分布をもとに観測値から尤度を計算してコストに換算すれば、あとは最適化関数を用いて必要なパラメータを学習させればいいことになります。
features = tf.placeholder(dtype=tf.float32,shape=[None,4])
target = tf.placeholder(dtype=tf.float32,shape=[None,3])
weight = tf.Variable(tf.truncated_normal([4,3]))
bias = tf.Variable(tf.zeros([3]))
def logistic_model(x) :
p = tf.nn.softmax(tf.matmul(x,weight) + bias )
observe = tfp.edward2.Multinomial(total_count=1,probs=p,name='observe')
return observe
prob = logistic_model(features)
log_joint = tfp.edward2.make_log_joint_fn(logistic_model)
cost = -log_joint(features,observe=target)
train = tf.train.AdamOptimizer().minimize(cost)
回帰のモデルをベースに考えると改修すべきポイントは感覚的につかめるかと思います。ポイントはモデルの本体であるlogistic_modelです。最終的な出力値であるobserveがedward2.Multinomialから出力されるようにしています。これはsoftmaxを使って各クラスの出現確率を計算したうえでその結果をもとにした多項分布としてモデル化しています。
学習後の予測の際はprobを使って計算できます。ただし、関数には確率モデルを加えているので1回の計算では偶発性が強く出てしまうので回帰のときと同様に1000回程度の計算を行った結果から判断したほうがいいかと思います。
MCMC
最尤推計のモデルが実装できれがMCMCへの移行は容易です。先の回帰の実装を参考にモデルの改良・尤度計算の関数の改良、学習アルゴリズム部分の追記、iteration部分の追記を行えば完了です。
features = tf.placeholder(dtype=tf.float32,shape=[None,4])
target = tf.placeholder(dtype=tf.float32,shape=[None,3])
def logistic_model(x) :
w_scale = tfp.edward2.Cauchy(0,1,name='w_scale')
b_scale = tfp.edward2.Cauchy(0,1,name='b_scale')
weight = tfp.edward2.Normal(loc=tf.zeros([4,3]), scale=w_scale, name="weight")
bias = tfp.edward2.Normal(loc=tf.zeros([3]), scale=b_scale, name="bias")
p = tf.nn.softmax(tf.matmul(x,weight) + bias )
observe = tfp.edward2.Multinomial(total_count=1,probs=p,name='observe')
return observe
log_joint = tfp.edward2.make_log_joint_fn(logistic_model)
def target_log_prob_fn(w_scale, b_scale, weight, bias):
return log_joint(x=features,
w_scale=w_scale,
b_scale=b_scale,
weight=weight,
bias=bias,
observe=target)
w_scale_init = tf.get_variable('w_scale',[1])[0]
b_scale_init = tf.get_variable('b_scale',[1])[0]
weight_init = tf.get_variable('weight',shape=[4,3])
bias_init = tf.get_variable('bias',shape=[3])
hmc = tfp. mcmc.HamiltonianMonteCarlo(
target_log_prob_fn=target_log_prob_fn,
num_leapfrog_steps=3,
step_size=tf.Variable(0.01),
step_size_update_fn=tfp.mcmc.make_simple_step_size_update_policy(1))
[
[w_scale, b_scale, weight, bias],
kernel_results
] = tfp.mcmc.sample_chain(
num_results=8000,
num_burnin_steps=800,
current_state=[w_scale_init, b_scale_init, weight_init, bias_init],
parallel_iterations=500,
kernel=hmc)
weight_trans = tf.reduce_mean(weight,axis=0)
bias_trans = tf.reduce_mean(bias,axis=0)
prob_class = tf.nn.softmax(tf.matmul(features,weight_trans) + bias_trans)
なお、新たな改修として、w_scaleとb_scaleをモデル内で定義するとともにMCMCによる学習対象とするコードを加えました。これら、stanを使ってIRISのモデル実装のサンプルコードに着想を得たもので、weightとbiasをうまくサンプリングできるようにするための事前分布にあたるものです。
weihgtパラメータの収束状況を以下に示します。なお、見やすくするために平均を引いています。
これによると、パラメータはあまりうまく収束していないようです。ただし、prob_classをもとに予測すると結果は以下のようになり、うまくモデル化できているようです。
| 予測値=0 | 予測値=1 | 予測値=2 | |
|---|---|---|---|
| 観測値=0 | 50 | 0 | 0 |
| 観測値=1 | 0 | 46 | 4 |
| 観測値=2 | 0 | 0 | 50 |
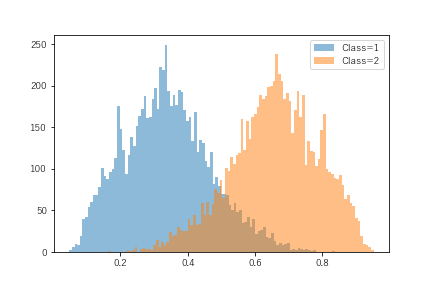
weightおよびbiasともに8000回のサンプリングをしているので、その組み合わせから各クラスの確率を8000回をサンプリングできます。これは各クラスに属する確率の分布という意味合いになります。今回、うまく予測ができなかったデータをひとつ取り出して、確率の分布を可視化します。
分布の重なる部分がそれなりにあります。つまり、点推計としてのClass=2に属する確率ほど、確信が持てていないことがわかります。ただし、この分布の確からしさはモデルパラメータが安定的にサンプリングできていることが前提となります。
まとめ
TFPによるMCMCであっても順を追っていけばそれほど難しいものではありません。ただ、ここで示したものは入り口です。先人のコードはここから更に発展したものがあがっています。
個人的には、階層ベイズと呼ばれるものはニューラルネットワークと相性が良さそうなのでtensorflowベースで実装できるになりたいです。そのためには事前分布をうまく使いこなさないとパラメータが収束しないことはstanで経験していることです。その意味でもtensorflow上で事前分布をうまく設定する方法・ノウハウを研究したいと思っています。