以前、こちらの投稿
https://qiita.com/ryouta0506/items/100a2b252fbaeb73f493
でJリーグの対戦結果を予測するモデルをStanを使って構築した結果を報告しました。結果は「もう少し頑張りましょう」というものでした。ニューラルネットやランダムフォレストなどの機械学習に切り替えてチャレンジするという選択肢もあるのですが、私としてはもうしばらくStanで粘ってみたいと考えています。ただ、そのためには私自身のStanを使ったモデリングスキルをレベルアップする必要があります。
そこで、緑本(正式には「データ解析のための統計モデリング入門」)の著者である久保先生がyoutubeの動画のなかで緑本の次に読むべきものとして紹介していたThe BUGS bookを題材に勉強することにしました。BUGS bookのコードは全てBUGSで書かれています。つまり、このコードを解説を見ながらstanへと移植すれば、知識とともにコードの書き方がレベルアップするであろうという発想です。
購入して勉強しながらいろいろと試してみましたが、やはりためになりました。そこで、BUGSからStanへの移植結果のコードを自身の記録とこれからStanを使ったモデリングに取り組もうとする方々向けに公表したいと思います。
はじめに
移植対象は自身が興味を持ったものに限っています。よって全コードは網羅していません。主だったものは網羅していますが、以外と重要なものが抜けていることもありますがご了解ください。
私自身はBUGSを使った(書いた)ことがありません。関数についてはAppendixに説明があるので、こちらを確認しながら該当するStanの関数に置き換えるという方法で対処しています。また、本文の解説をもとに実現したいことをつかみ、BUGS bookと異なるアプローチとさせてもらった部分もあります。よって掲載するコードは逐語訳のようなものにはなっていません。
なお、私のBUGSおよびその関連知識のため、元のコードを誤って理解している部分もあるかと思います。また、BUGS bookは英文なのでこの部分に起因する誤解もあるかと思います。そうした部分がありましたらぜひともご指摘いただけるとありがたく思います。
最後に実行環境を以下に示します。
OS :Win10
python :3.6
pystan :2.17.1
compiler:MingW-w64
compilerですが、msvcだとコンパイルエラーとなる構文があります。stanの公式サイトでもmsvcはサポートしていませんと明示されているので注意してください。
Monte Carlo simulation using BUGS
第1章はイントロダクションなのでとりあえず省略し、第2章から始めます。題名からすると、Monte Carlo simulationについて取り扱っているように思えますが、実際はBUGSをMonte Carlo simulationを例示に紹介している章というトーンです。つまり、Monte Carlo simulationをある程度わかっている人に向けてBUGSだとこんな感じになりますという紹介をしている章になっているという意味合いです。
まずは、この章の例題コードを示し、Monte Carlo simulationがやろうとしていることを示したいと思います。
example 2.4.1
変数ZとYはY=(2Z+1)^3という関係にある。このZは平均=0、標準偏差=1の正規分布にしたがって出現する場合、Yが10より大きい値となる確率はどの程度か。
解析的に解くと、10<(2Z+1)^3からZの取り得る範囲を求め、その結果をもとに正規分布からZの取り得る確率を求めることになります。正直なところ、計算は面倒そうです。そこで、Zを乱数器から無数に取得して計算式に代入することでYの分布を擬似的に作り出します。乱数器から無数に生成した値は平均=0、標準偏差=1に近似した分布を取るのでこれを使って計算したYは、式Y=(2Z+1)^3のYに正規分布の関数を代入した結果と近似するということになります。つまり、Monte Carlo simulationはあらかじめわかっている乱数器から乱数を生成し、所定の計算(関数)の分布を計算するというものと言えそうです。
では、さっそく実装します。
stan_model ="""
data {
real mu; // Zの平均
real sigma; // Zの標準偏差
}
model {
}
generated quantities {
real Z ;
real Y ;
x = normal_rng(mu,sigma); // Xのサンプリング
Y = pow(2*Z+1,3); // XをもとにしたYのサンプリング
}
"""
もとのコードだと平均・標準偏差はOn Codingでしたが、気持ちの問題で外からデータとして引き渡されるものとしました。今回、求めたいものはYですが、これは最終的に生成するquantitiesなのでgenerated quantities部で計算させています。今回は求めるべきパラメータがないのでparameters部は省略しています。ただし、model部(パラメータを推計するためのモデルを定義する)は省略するとコンパイルエラーとなるので形だけ残しています。なお、元のコードはY>10のケースをカウントするコードが付加されていましたが、サンプリングさえできれば、以後はpython側で対応できることなのでコードにしていません。
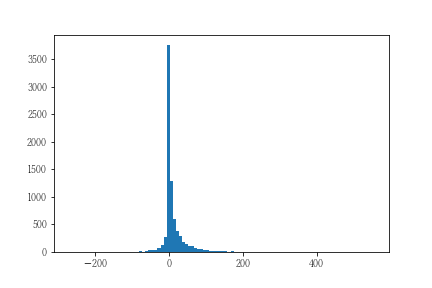
結果は以下のようになりました。
あとは、このデータから所定の条件を満たす件数の割合を計算すれば結果となります。
example 2.5.1
ある設備の1回あたりの修理費は、平均=100(ポンド)、標準偏差=50(ポンド)のガンマ分布に従う。ある期間の修理予算が1000(ポンド)とした場合、修理可能な回数はどの程度か
この例題は修理費の分布の定義で若干の手間が必要です。gamma分布の形状パラメータは平均および標準偏差そのものではないので、所定の計算式にしたがってパラメータを特定する必要があります。ここさえクリアできれば、後はコードにするだけです。
stan_model ="""
data {
int<lower=0> N; // 試行回数
real alpha; // gamma分布のパラメータ
real beta; // gamma分布のパラメータ
}
model {
}
generated quantities {
real ucost ; // 単位あたりの修繕費
real K ; // 修理回数
real tcost; // トータル修繕費
K = 0;
tcost = 0;
for (i in 1:N) {
ucost = gamma_rng(alpha,beta);
if ((tcost+ucost)<=1000) {
K = K+1;
tcost = tcost + ucost;
}
}
}
"""
ucost=の部分でgammma分布から乱数を生成し、トータルコストが1000超ならない限り、修繕可能としています。
実際の実行処理のコードを合わせて記載します。
# alpha,betaはガンマ分布における平均と分散の定義をもとに方程式の解より設定
# 平均(=100) = alpha / beta
# 分散(=50^2) = alpha / beta^2
stan_data = {'alpha':4,
'beta':0.04,
'N':20}
result = st.sampling(data=stan_data,algorithm="Fixed_param", warmup=0)
コードに記載したとおり、alpha,betaのパラメータは上記にて定義づけられるので連立方程式を解けば得られることになります。実際には、生データを読み込んで直接的にalpha,betaを決定するケースのほうが多いはずなので、あまり気にする必要はないかと思います。
シミュレーションの結果を示します。
まず、設定された予算(1,000ポンド)で修理可能な回数の分布は以下となります。
平均が100ポンド、総予算が1000ポンドでしたから想定どおりの結果です。ただし、10回以上となるケースも相当存在するので、予算に加えて修理回数も制約条件にすると思ったように修理できないケースが頻発しそうということもわかります。
Regression Models
この章に至るまでに"Introduction to Beyesian Inference"、"Introduction to MCMC","Prior Distributions"が挟まります。このうちPrior Distributionは実装面で重要なのですが、個人的に惹かれた例示がなかったので、実際のモデルにおいて取り扱います。
example 6.1.1
Ratの成長の記録を取ったデータから成長率を表すモデルを定義する。
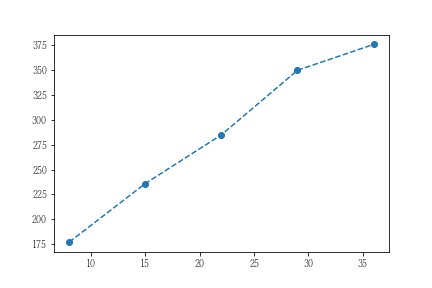
まず対象データを可視化します。なお、データはBUGS bookの公式サイトから取得しました。
典型的な回帰モデルです。BUGS bookでは説明変数にx-mean(x)を用いています。実務上はpython側でsklearnのStandardScalarで標準化した上で学習させるほうがいいように思いますが、ここではBUGS bookのコードの通りに実装します。
stan_model = """
data {
int N ; // num of data
vector[N] D ; // days
vector[N] W ; // weight
}
transformed data {
real mu ; //mean of day
vector[N] Dr ;
mu = mean(D[]) ;
for (i in 1:N) {
Dr[i] = D[i] - mu ;
}
}
parameters {
real a1 ; //coef
real b1 ; //intercept
real sigma1 ;
}
model {
W ~ normal(a1*Dr+b1,1/exp(sigma1*2)) ; // BUGS book
}
generated quantities {
real Pw1[N] ;
for (j in 1:N) {
Pw1[j] = normal_rng(a1*Dr[j]+b1,1/exp(sigma1*2)) ;
}
}
"""
コードの考え方ですが、モデルの理論値を平均値、sigama1を標準偏差とした正規分布にしたがうと仮定し、モデルパラメータ(a1,b1)およびsigmaをMCMCを使って推計します。
この際、a1,b1,sigma1の事前分布をどのように定義するかが問題です。この事前分布はMCMCからいうと、シミュレーションをするための乱数器の意味合いを持ちます。よって事前の分析によって理解している情報をもとに事前分布を設定することで収束の早期化と結果の適正化に導くことができるようになります。
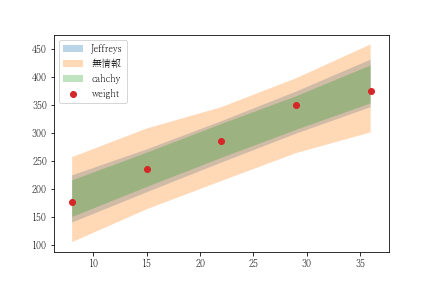
事前の情報がない場合、無情報事前分布という-∞~+∞の値が同じ確率で出現するような分布を用います。(Stanの場合は省略すると無情報事前分布と解釈します)実際に無情報事前分布として学習させると、標準偏差は23.49という大きな値を取ります。一方、BUGS bookではJeffreys分布を適用することで、一種の制約を与えることでsigma1が過度に大きくならないようにしています。なお、関西学院大学の清水先生は、以下の資料において標準偏差の事前分布にcauchy(0,5)を用いることで無情報でも不確実性が大きくならないような工夫をしています。
この3パターンで学習させた場合の範囲推計結果を以下に示します。
example 6.3.1
Dugongの年齢と体長の記録データから年齢と体長の関係を表すモデルを定義する。
まず、データを可視化します。
実際の予測モデルですが、Von Bertalanffyの成長モデルを用いることになっています。
y=Linf - (Linf-L0)exp(-Kage)
y:予測対象体長 , Linf:生涯に到達する体長 , L0:生後の体長 , K:モデルパラメータ , age:年齢
ご覧の通り、本当に推計しなければならないパラメータはKなのですが、実際にはLinfやL0も推計する必要がある非線形なモデルとなっています。
stan_code = """
data {
int N ; // num of data
real age[N] ;
real Lo[N] ; // Length observed
}
parameters {
real<lower=0> L0 ; // 生まれたときの体長
real<lower=0> Lg ; // 成長分
real<lower=0> sigma ; // Lengthの標準偏差
real K ; // model parameter
}
transformed parameters {
real Linf ; // 生涯の体調
Linf = L0 + Lg ;
}
model {
real mu[N] ;
sigma ~ cauchy(0,5) ;
for (i in 1:N) {
mu[i] = Linf - (Linf-L0)*exp(-K*age[i]) ;
Lo[i] ~ normal(mu[i],sigma);
}
}
generated quantities {
real Lp[N] ;
for (j in 1:N) {
Lp[j] = normal_rng(Linf-(Linf-L0)*exp(-K*age[j]),sigma) ;
}
}
"""
BUGS bookでは2通り指数部の書き方が異なるモデル×2通りの事前分布の4通りが記載されています。よってこのうちの2通りは本質的な差異はなりませんし、事前分布の件も既に示した通りなので、ここではBUGS bookに掲載されている数式をそのままモデルに落とし込むことにして標準偏差についてはcauchy分布を使うことにしました。
example 6.5.1
ある化学化合物に5時間されたときにbeetleの死亡率を表すモデルを定義する。
BUGS bookに記載されているモデルの構造は以下の通りです。
y(死亡数) ~ binomial(p,n(被験数)) , logit(p) = a + b(x-mean(x))
BUGSの場合、logit(p) = a + b(x-mean(x))をそのまま実装してもうまく解釈してp=…に置き換えて計算してくれるようですが、Stanの場合は左辺に関数を置くことができません。よって式変形をする必要があります。実際にはlogit関数の逆関数に置き換えることで対応させています。
stan_code = """
data {
int N ; // num of data
real x[N] ; // x
int n[N] ; // observation
int y[N] ; // deth
}
transformed data {
real mu ;
real x_t[N] ;
mu = mean(x[]) ;
for (i in 1:N) {
x_t[i] = x[i] - mu ;
}
}
parameters {
real alpha ;
real beta ;
}
model {
real p ;
for (j in 1:N) {
p = inv_logit(alpha*x_t[j]+beta);
y[j] ~ binomial(n[j],p);
}
}
generated quantities {
real p_p[N] ;
int yp[N] ;
for (k in 1:N) {
p_p[k] = inv_logit(alpha*x_t[k]+beta);
yp[k] = binomial_rng(n[k],p_p[k]);
}
}
"""
上記のうち、
p = inv_logit(alpha*x_t[j]+beta);
y[j] ~ binomial(n[j],p);
の部分ですが、binomial_logit(n[j],alpha*x_t[j]+beta)とまとめて表記することも可能です。ただ、x_tは平均値を使って調整した値のため、計算結果が負値を取ることがあるのでエラーになってしまいます。よってbinomial_logitを使う場合は、transformed dataによる数値変換を止めて、読み込んだデータをそのままモデルに使うように修正する必要があります。
example 6.5.2
Salmonellaに対し変異性をもつ投薬を量を変えながら実施した結果より投薬と変異したSalmonellaの復元数との関係をモデル化する。
データは以下の通りです。
| 0 | 10 | 33 | 100 | 333 | 1000 | |
|---|---|---|---|---|---|---|
| Plate1 | 15 | 16 | 16 | 27 | 33 | 20 |
| Plate2 | 21 | 18 | 26 | 41 | 38 | 27 |
| Plate3 | 29 | 21 | 33 | 60 | 41 | 42 |
モデル化にあたってのポイントは、1)Salmonellaは生物なので常に正であること、2)投薬量が多くなると結果(変異から復元したSalmonella数)のバラつきが大きくなること、があげられます。この場合、従来の回帰モデルだと切片の値によってはマイナスを取ることが起こるので不都合です。加えていうと、従来の回帰モデルは誤差が正規分布を前提にするので、投薬量が大きくなっても誤差分布は変化しません。
BUGS Bookでは、「GLMの理論にしたがって」とサラリと前置きをした上で、以下の定式化を示しています。
y(復元したSalmonella菌数) ~ Poisson(期待値) ---①
log(期待値) = a + b log(10+投薬量) + c 投薬量 ---②
式の意味を考えずにコードを書いてもいいのですが、モデルが何を表現しているのかを確認したいと思います。
まず、①は誤差込みの結果を定式化したもので、誤差がポアソン分布に従うことを意味します。ポアソン分布は、常に正の値を取るとともに期待値=分散を前提とする分布のため、②によって計算される結果が大きくなるにつれてバラつきを大きくすることができます。
続いて②ですが、log関数の逆関数であるexp関数を使って式変換します。
期待値 = exp(a + b log(10+投薬量) + c 投薬量)
これを更に指数関数の公式にしたがって式変形します。
期待値 = A×(10+投薬量)^B×C^投薬量
ただし、A=exp(a) , B=exp(b) , C=exp(c)とする。
この式から、Aは初期値、Bは自然増率、Cは投薬量に応じた像率、を表していると解釈できます。このように増率をexp関数で表現することで、マイナス値を取らないモデルにすることができます。
では実装です。
stan_code = """
data {
int ROW ;
int COL ;
int D[ROW,COL] ;
real x[COL];
}
parameters {
real alpha ;
real beta ;
real gamma ;
}
transformed parameters {
real mu[COL] ;
for (j in 1:COL) {
mu[j] = alpha + beta*log(x[j]+10) + gamma*x[j] ;
}
}
model {
for (k in 1:ROW) {
for (l in 1:COL) {
D[k,l] ~ poisson_log(mu[l]) ;
}
}
}
"""
若干解説すると、ポアソン分布に設定する期待値は、transformed parameters部で計算していますが、model部でも構いません。また、muの計算時にexpを適用していません。その代わりにpoisson_logを用いています。
さてBUGS Bookでは、この例題に対して「負の二項分布」を用いるアプローチも記載されています。この例題の場合、平均と分散が近似しておらず、過分散と呼ばれる状態です。こうしたときは負の二項分布を使うとうまくいくということです。
負の二項分布は、呼び名からすると二項分布の系統に思えますが、ポアソン分布から導出されるもので、ポアソン分布の平均と分散を切り離した一般形とでもいうべきものです。この負の二項分布をBUGSからStanに書き換える場合、ちょっとした問題があります。
まず、負の二項分布そのものに複数の定義が存在するので、BUGSとStanで同じとは限りません。
詳細はこちらを参照 :
https://en.wikipedia.org/wiki/Negative_binomial_distribution
くわえていうと、仮に同じだとしても双方で設定するパラメータが異なるのであれば変換してから設定する必要があります。そこで、BUGS Bookを移行することはあきらめて、問題設定からコードを書き起こすことにしました。
stan_code = """
data {
int ROW ;
int COL ;
int D[ROW,COL] ;
real x[COL];
}
parameters {
real alpha ;
real beta ;
real gamma ;
real phi ;
}
transformed parameters {
real mu[COL] ;
for (j in 1:COL) {
mu[j] = exp(alpha + beta*log(x[j]+10) + gamma*x[j]) ;
}
}
model {
real sigma ;
for (l in 1:COL) {
sigma = mu[l]+phi;
D[,l] ~ neg_binomial_2(mu[l],pow(mu[l],2)/(sigma-mu[l])) ;
}
}
"""
Stanには負の二項分布を表す関数が2つほど用意されています。今回はそのうちのneg_binomial_2を使用しています。設定するパラメータですが、以下の条件を満たす2つを設定する必要があります。
期待値=mu
分散=mu+mu^2/phi
muは、モデルのなかで計算したものをそのまま使えるので、あとは分散の計算式からphiを計算すればいいことになります。(pow(mu[l],2)/(sigma-mu[l])がこのphiにあたります。)この際、分散(sigmaに相当)は与えられていないのでモデルパラメータとともに推計すべき対象としました。
個人的には、この負の二項分布は勉強になりました。元々の目的であるサッカーのスコア予測の際、今のモデルはポアソン分布を用いていますが、どうしても平均値が小さいため2点・3点の確率がほとんどないようになっています。そこで、過分散であると仮定して負の二項分布をうまく適用することができれば、もう少し精度があがるように思われます。
Categorical Data
この章はカテゴリーデータを取り扱います。回帰モデルにおいてロジスティック回帰を扱っていることも影響して、この章は15ページほどです。
example 7.1.1
2種類のミルクティー(「紅茶を先に注ぎ、ミルクを後にしたもの」と「ミルクを先に注ぎ、紅茶を後にしたもの」)についてテイスティングした結果から、テスターが正しく識別できるているかどうかを評価する。
データは以下です。(縦軸がテスターの判断、横軸は実際の入れ方)
| milk | tea | |
|---|---|---|
| milk | 3 | 1 |
| tea | 1 | 3 |
見た感じからするとうまく識別できているようです。しかしながら、カイ二乗検定(scipi.statsの関数を活用)を行うとP-value=0.479となり、偶然の可能性を排除できませんでした。これは、縦計・横計から、[[2,2]],[2,2]]を基準に偶然の可能性を評価するものなので、このくらいのデータ件数だと仕方ないのかもしれません。
これに対し、BUGS Bookは二項分布を活用した方法が紹介されています。つまり、milkを先にしたミルクティーを正しく識別できる確率をθ1として、4回の試行のうち3回成功させる確率をMCMCによって推論しようというものです。そして同じことをteaを先のミルクティーに実施して、差異を評価するというものです。この分布から0より大きくなっていれば、テスターがmilkを先に注いだティーを正しく識別できていると判断します。
BUGS Bookではこの推計を行うにあたって無情報事前分布とBeta分布の2ケースが紹介されているので、同じように実装します。
stan_code = """
data {
int ROW ; // 行数
int COL ; // 列数
int D[ROW,COL] ; // データ本体
}
parameters {
vector<lower=0,upper=1>[2] P1 ; // 無情報事前分布のケース
vector<lower=0,upper=1>[2] P2 ; // Beta分布のケース
}
transformed parameters {
vector[2] residual ;
residual = P1 - P2 ; // Milkが先とする確率の差異
}
model {
// 無情報事前分布
D[1,1] ~ binomial(D[1,1]+D[1,2],P1[1]) ;
D[2,1] ~ binomial(D[2,1]+D[2,2],P2[1]) ;
// Beta分布
P1[2] ~ beta(0.5,0.5) ;
P2[2] ~ beta(0.5,0.5) ;
D[1,1] ~ binomial(D[1,1]+D[1,2],P1[2]) ;
D[2,1] ~ binomial(D[2,1]+D[2,2],P2[2]) ;
}
"""
どちらのケースでもMilkを先に注いだティーをそのように識別する確率が高くなりました。参考までにコードでいうP1とP2の差異を可視化したものを載せます。

example 7.2.1
ある2時点の喘息の症状を測定し、その遷移を集計した結果から状態遷移行列を求める。
データは、以下の通りです。(縦軸がFromで横軸がTo)
| STW | UTW | Hex | Pex | TF | |
|---|---|---|---|---|---|
| STW | 210 | 60 | 0 | 1 | 1 |
| UTW | 88 | 641 | 0 | 4 | 13 |
| Hex | 0 | 0 | 0 | 0 | 0 |
| Pex | 1 | 0 | 0 | 0 | 1 |
BUGS Bookは、この状態遷移行列を多項分布を用いて推計するアプローチを紹介しています。つまり、ある時点のSTWという症状の総数が次の時点でどの症状になるのかを多項分布を用いて求めようというものです。なお、横軸のTFはTreatment Failureを意味しており、その後のモニタリングを行っていないため、縦軸に表現されていません。
コードは以下のようになります。
stan_code = """
data {
int ROW ;
int COL ;
int D[ROW,COL] ;
}
parameters {
simplex[COL] P[ROW] ;
}
model {
vector[COL] alpha;
for (i in 1:COL) {
alpha[i] = 1 ;
}
for (j in 1:ROW) {
P[j][] ~ dirichlet(alpha) ;
D[j,] ~ multinomial(P[j][]) ;
}
}
"""
各カテゴリーに属する確率Pはトータルで1.0となる必要があるものなので、simplexという制約付きベクトルを定義します。また、事前分布にはdirichlet分布を使用しています。コードにしていませんが、generated quantities部で結果として取得した状態遷移行列を繰り返して適用すれば、将来の患者数を推計することもできます。
この状態遷移行列を複数の多項分布によって推計する方法は私にとって参考になりました。サッカーの得点を推計するモデルにこのアプローチが使えるかもしれません。ただ、実装するとなると、得点の取る範囲を限定する必要があるとともに各カテゴリに属する確率をどうやって定式化するのかがポイントになりそうです。
まだ、BUGS Bookの半分くらいですが、いったんここで終了とします。
最後に、ここで示したコードに使用するデータは、以下のBUGS Bookの補足用のサイトにありますので適宜確認してください。