はじめに
データ分析のスポーツ適用は今では常識的になっています。データスタジアムという専門会社が既に存在してTVなどで活躍しています。また、日本スポーツアナリスト協会という社団法人が創設され、アナリストの育成が進められています。このQiitaでもスポーツをキーワードで検索すると、なかなかの投稿がヒットします。
そこで、私も何かやってみたいと思い、Jリーグを事例に行った結果を報告したいと思います。この記事を目にして更に進化した分析やオリジナルの取り組みが増えていくと大変うれしく思います。
分析の視点
分析の最終ゴールは、試合の勝敗予測に置きます。ワールドカップなどになると試合前日のスポーツコーナーで解説者が「日本は勝てます」という客観的評価とも希望ともいえるような予測を立てるのを観て、もう少し客観的な評価をしてくれるような予測モデルがあってもいいと感じたことが動機になっています。
勝敗を予測する予測モデルには、予測対象を「勝ち」・「負け」・「引分」の他クラス分類があります。ただ、これであると予測モデルの出力がこの3クラスしかなく、これから試合観戦する側からすると面白くありません。観戦者からすると勝敗を決定するキーポイントを示してくれるとそこに着目して観戦できるので、さらに試合を楽しめるはずです。
また、スポーツは単純な実力差だけで勝敗が決定するものではありません。特にサッカーのように手をつかわずにボールをコントロールする必要のある球技の場合、観戦者すると不運(プレイヤーからするとミス)によって得点や失点するケースが存在します。こうした偶発的なケースも踏まえた予測がモデルによって出力できると、最終的な結果に対する認識(たまたま勝てた・実力差で負けた)を深めることが期待できます。
よって、予測モデルの最終ゴールは、スコア2-0(確率40%)・2-1(確率35%)・2-2(確率15%)といったようにスコアと発生確率をセットで出力するようなモデルを構築することに置きます。そして、今回の報告は、こうしたモデルの構築を念頭に2018年のJリーグを振り返ります。
得点はなぜ入るのか
スコアを予測するモデルを構築するためにはこの「なぜ得点は入るのか」について定式化する必要があります。
最も抽象的にいうならば、双方のチーム(ホームチームとアウェイチームをする)の攻撃力と守備力の差ということになります。つまり、ホームチームの攻撃力がアウェイチームの守備力を上回れば得点シーンが増えて多くの得点が入り、その反対であれば0点に抑えられる可能性が高まります。ただ、ホームチームとアウェイチームの差がそのまま得点(あるいは失点)となるわけではありません。先にも述べたように偶然(プレイヤーにとってはミス)が入り込む余地があることから、ホームチームの攻撃力がアウェイチームの守備力を上回ったからといって直ちに得点となりません。つまり、その差が2倍になったからといって線形に得点が増加するものではありません。
そこで、本モデルはホームチームとアウェイチームの攻撃力と守備力の差をベースに確率分布にしたがってホームチームの得点が入るという構造を採用します。同様にアウェイチームの得点(ホームチームからすると失点)は、アウェイチームの攻撃力がホームチームの守備力を上回る度合いに応じて変化する確率分布にしたがう構造とします。こうすることで、彼我の攻撃力と守備力の差が得点シーンそのものの数に影響し、何らかの確率分布にしたがって得点(または失点)するというものにすることで1試合中に発生する偶発的事象を表現したいと思います。
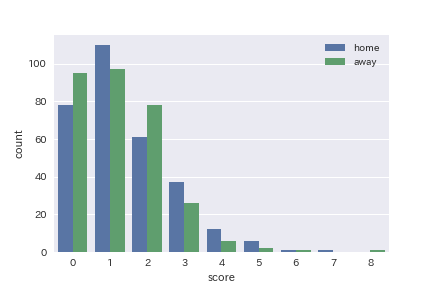
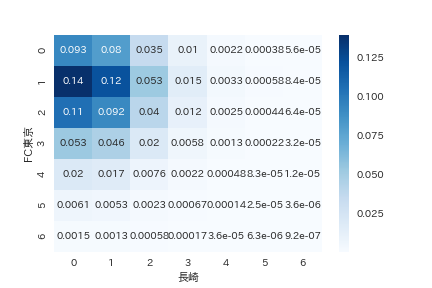
では、この得点を産む確率分布とはいったいどのようなものなのでしょうか。以下は、2018年度の各試合の得点分布を可視化したものです。
これより、(1)スコアなので当然ですが、変数は非負である、(2)変数は1~8の範囲に収まり、実質的に離散値の分布である、(3)最頻値が0のほうに偏っている、という特徴が見えます。この特徴から得点はポアソン分布に従うものとしてモデル化します。
実際のモデルは以下とします。
ホームチームの得点 ~ poisson(ホームチーム攻撃力 - アウェイチーム守備力)
アウェイチームの得点 ~ poisson(アウェイチームの攻撃力 - ホームチームの守備力)
さて、サッカーにおいてサポーターは12番目の選手という言葉がある通り、ホームチームのほうが何らかの有利性を持っていると考えられます。そこで、上記のモデルにホームアドバンテージという変数を含めたいと思います。
ホームチームの得点 ~ poisson(ホームチーム攻撃力 - アウェイチーム守備力 - ホームアドバンテージ)
アウェイチームの得点 ~ poisson(アウェイチームの攻撃力 - ホームチームの守備力 - ホームアドバンテージ)
モデルの実装
先に述べたような確率分布を表現するには、ベイズ推計に基づくMCMCが適しています。そこで、pystanを使ってモデリングすることにしました。pystanはバックエンドでstanを使用するラッパーのようなモジュールです。おおよそのコーディングの流れは、(1)stanの文法にしたがいモデルを記述、(2)pystanからCのモジュールを生成、(3)stanにインプットするデータを作成し、pystanを経由して学習、というものです。
先の定式化したモデルを以下のstanコードで表現します。
model_code = """
data {
int N; // N Games
int K; // K Teams
int home_team[N]; // Home Team ID
int away_team[N]; // Away Team ID
int ht_score[N]; // Home Team score
int at_score[N]; // Away Team score
}
parameters {
real<lower=-1,upper=1> atk[K]; // atack
real<lower=-1,upper=1> def[K]; // defence
real<lower=0> home_adv[K]; // home advantage
real<lower=0> sigma[K]; // sigma
real<lower=0> hadv_sigma; // sigma home_advantage
}
model {
for (k in 1:K) {
atk[k] ~ normal(0, sigma[k]);
def[k] ~ normal(0, sigma[k]);
home_adv[k] ~ normal(0, hadv_sigma);
}
for (n in 1:N) {
ht_score[n] ~ poisson(exp(
(home_adv[home_team[n]] + atk[home_team[n]]) - (def[away_team[n]])
));
at_score[n] ~ poisson(exp((atk[away_team[n]]) - (def[home_team[n]] + home_adv[home_team[n]])
));
}
}
"""
簡単にモデルコードを解説します。stanのコードは、data部・parameters部・model部で構成されます。
data部は入力データに関する定義をする部分です。変数Nは、入力データを配列として格納するための次元数を意味しています。また、Kは分析対象のチームに割り振られているIDの数を定義したものです。home_teamやht_scoreはデータの実態です。今回はいずれもスカラーとして定義しましたが、vectorとして[N,4]という形態でまとめて定義することも可能です。
prameters部は推計対象のパラメータを定義する部分です。推計対象は、各チームの攻撃力・守備力・ホームアドバンテージとしました。この際、攻撃力と守備力は-1~1の範囲に収まるものとして制約を付けました。これによりうまく収束することを期待します。また、ホームアドバンテージは非負という制約を付けました。サンプリングによってホームアドバンテージが負の値をとることが起こりえます。スコアの予測モデルの特性上、ホームアドバンテージが負であるとホームゲームのほうが不利になってしまいます。もちろん、そういうチームもあり得るでしょうが、ホームアドバンテージという言葉の通り、非負とすることでホームゲームではホームチームが常に有利になるようにしました。
model部が実際のモデル部分であり、学習部分にあたります。モデルの学習は定義すれば、stan側で必要な計算処理を全て行ってくれます。このmodel部にatk・def・home_advが正規分布に従うとしたコードが追加されています。この部分のコードはなくても学習可能なのですが、実際にそのようにしたところ、学習が収束しませんでした。そこで、各々のパラメータについて事前分布をとるモデルとすることでうまく収束させてました。この事前分布ですが、ベイズ推計的にいうと主観確率を設定すればいいことになっているので、平均0・分散はサンプリングで決定される正規分布としました。(そのため、パラメータ部にsigmaなどを定義しています。)
また、ポアソン分布のパラメータは正値しかとれないので、攻撃力と守備力の差がマイナスをとるケースへの対応が必要となります。そこで、この差異を指数関数に入力することで常にポアソン分布のパラメータが0以上となるようにしました。
完成したモデルは、コンパイル・実行という順序で進めるようにpythonコードを記述します。
import pystan
sm = pystan.StanModel(model_code=model_code)
team_name = data_2018['ホーム'].unique()
N = len(data_2018)
K = len(team_name)
stan_input = {'N':N,
'K':K,
'home_team':data_2018['home_team_id'],
'away_team':data_2018['away_team_id'],
'ht_score' :data_2018['home_team_score'],
'at_score' :data_2018['away_team_score']}
result = sm.sampling(data=stan_input,iter=6000,seed=1234,warmup=1000)
data_2018は、Jリーグのサイトから取得してきたデータを加工したものです。参考にサイトから取り込んだ元データを載せておきます。
| 年度| 大会| 節|試合日|K/O時刻|ホーム|スコア|アウェイ|スタジアム|入場者数|
|:----|:----|:-----|:-----|:-----|:-----|:-----|:-----|:-----|:-----|:-----|
|2018| J1| 第1節第1日| 02/23(金)| 20:03| 鳥栖| 1-1| 神戸| ベアスタ| 19633|
|2018| J1| 第1節第2日| 02/24(土)| 14:03| FC東京| 1-1| 浦和| 味スタ| 35951|
|2018| J1| 第1節第2日| 02/24(土)| 14:03| 広島| 1-0| 札幌| Eスタ| 17026 |
|2018 |J1| 第1節第2日| 02/24(土)| 14:33| G大阪| 2-3| 名古屋| 吹田S| 28681|
|2018 |J1 |第1節第2日| 02/24(土)| 16:03| 湘南| 2-1| 長崎| BMWス| 12148|
smはコンパイルを表すコードです。そしてsm.samplingが学習部分にあたります。sm.samplingに入力するデータは、辞書形式で定義します。stanコードのdata部で指定する変数名とキーを合わせるようにします。stanのmodel部にある通り学習はデータ件数分の繰り返しが基本になります。したがって、数十万件のデータがあると相当の時間が必要です。ここが欠点かもしれません。
学習結果とその分析
学習結果は、サンプリング結果を意味するオブジェクト(result)に収められています。サンプリングの結果のサマリを取り出してDataFrameの形式にすることは以下のコードで実現できます。結果は掲載しませんが、このなかのRhatを最初に確認します。この値によってパラメータのサンプリングが収束したことを判断します。
result_tbl = pd.DataFrame(result.summary()['summary'],
index=result.summary()['summary_rownames'],
columns=result.summary()['summary_colnames'])
次にこの結果を使って各チームの2018年の状況を可視化します。横軸に攻撃力・縦軸に守備力をとった散布図を描画します。マーカーの大きさでホームアドバンテージを表現します。
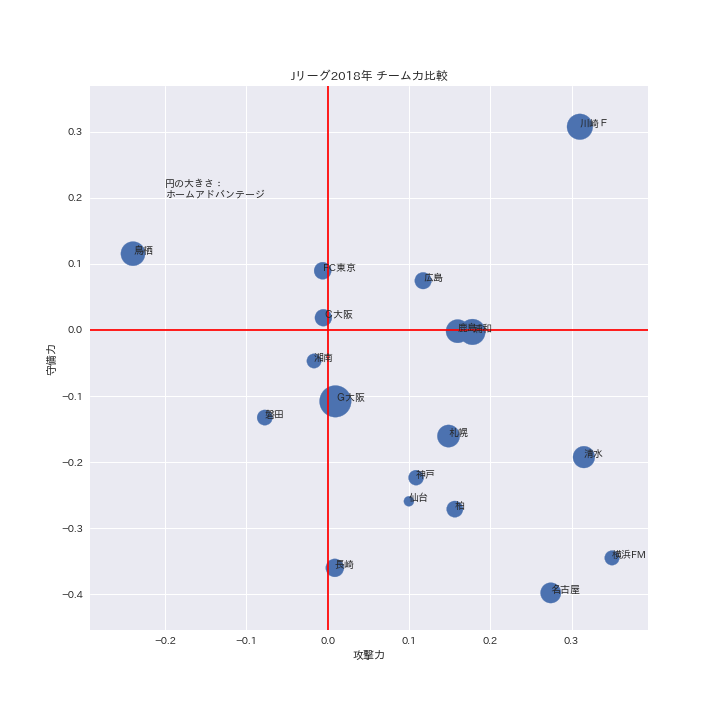
ここ数年、優勝争いに絡むチーム(川崎F・鹿島・浦和など)が右上に集中しており、縦軸に得点、横軸に失点として散布図を描いてもこれと近似したものになると想定できます。ただ、こちらのほうが、得点が自身の強さから来るものなのか、対戦相手の守備力に難があったものなのかが明確になっているので、より現実感覚に近いマップになっていると思います。
この攻撃力と守備力ですが、モデルの構造から正負で結果に与える影響が異なります。攻撃力の場合、正値は得点が獲得しやすくなり、負値であると0点で終わる可能性が高くなります。同様に守備力は正値であると失点を抑制する方向に働き、負値であると失点しやすくなります。したがって、攻撃力がプラスのチームが多い一方、守備力がマイナスのチームが多いということは、リーグ全体として攻撃力重視の方向であったことがうかがえます。
ホームアドバンテージを見てみると、G大阪・鹿島・浦和が上位に位置することがわかります。チームの攻撃力・守備力を補うほどのホームアドバンテージを確保sているチームは基本的にないようですが、鳥栖のホームアドバンテージはかなり上位となっており、攻撃力の弱点をそれなりに補った可能性が想定されます。
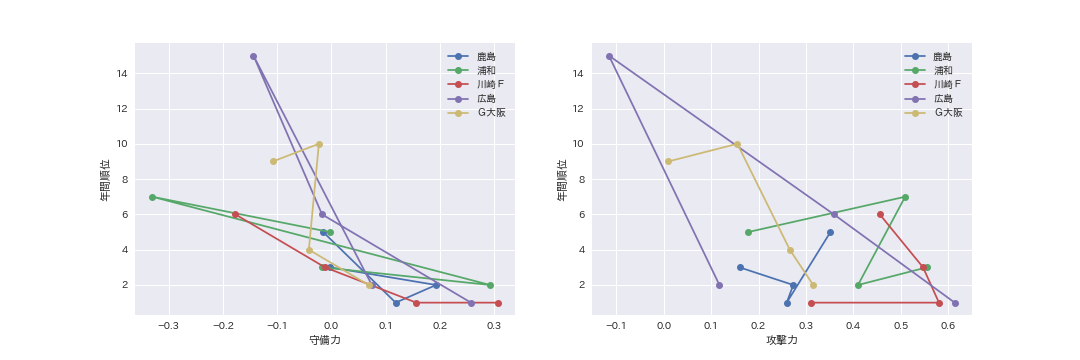
次に攻撃力と守備力のうち、通年の成績に影響するものはどちらなのかを分析するため、成績上位に食い込むことが多い鹿島・浦和・川崎F・広島・G大阪を対象に上記のモデルによる攻撃力と守備力の推計を2015年~2018年について実施し、その結果と順位の関係をプロットしました。
これから、守備力を強化したほうが、順位を高めることに影響していることがわかります。やはり、守備力を強化したほうがチームの安定性が高まり、通年の成績向上に貢献するのかもしれません。
スコアの予測
いよいよ本題であるスコアの予測を行います。stanには推計したパラメータ(各チームの攻撃力など)を用いたサンプリングをする機能がありますが、今回は単純にscipyに含まれるポアソン分布の関数を使って計算します。
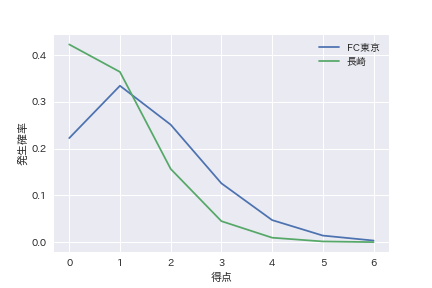
まず、ケーススタディとして川崎F対長崎(川崎Fホームゲーム)における両チームの得点を推計します。先に示した定式化にあるように得点はポアソン分布に従うのであらかじめ推計対象の得点を0~6として各得点が発生する確率を計算します。結果は以下のようになりました。
これから、長崎は0点となる確率が最も高く、川崎Fは1点となる確率が最も高くなっています。実際のスコアを取得したデータから確認したところ、「川崎F 1-0 長崎」となっており、うまくいきそうです。
実際に2018年の全試合について得点を推計してモデルの精度を確認します。以下は。縦軸に観測値、横軸に予測値としたホームチームの混合行列です。
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 15 | 61 | 2 |
| 1 | 12 | 96 | 2 |
| 2 | 8 | 51 | 2 |
| 3 | 5 | 31 | 1 |
| 4 | 0 | 12 | 0 |
| 5 | 0 | 5 | 1 |
| 6 | 0 | 1 | 0 |
| 7 | 0 | 1 | 0 |
次に、アウェイチームの混合行列を示します。
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 24 | 54 | 0 |
| 1 | 30 | 80 | 0 |
| 2 | 13 | 48 | 0 |
| 3 | 9 | 28 | 0 |
| 4 | 3 | 9 | 0 |
| 5 | 1 | 5 | 0 |
| 6 | 0 | 1 | 0 |
| 7 | 1 | 0 | 0 |
いずれも正解率が30%ほどということで、改善の余地が大いにあります。特に2点以上を予測するケースが極端に少ないことが問題です。4点以上は極めてレアケースとして割り切るとしても2点・3点の予測ケースがもう少し多くなるように改善する必要がありそうです。
今回の予測モデルの場合、各得点の発生確率が割り当てられています。そこで、正解に割当てられた確率値の平均を計算します。参考までにコードを掲載します。
# Stanの結果からサマリを取得し、チーム単位のDataFrameに整理しておく
result_tbl = pd.DataFrame(result.summary()['summary'],
index=result.summary()['summary_rownames'],
columns=result.summary()['summary_colnames'])
atk = result_tbl.iloc[0:18,0]
deff = result_tbl.iloc[18:36,0]
home_adv = result_tbl.iloc[36:54,0]
sigma = result_tbl.iloc[54:72,0]
result_tbl2 = pd.DataFrame({'team_name':team_name,'team_id':team_id,
'攻撃力':atk.tolist(),
'守備力':deff.tolist(),
'ホームアドバンテージ':home_adv.tolist(),
'攻守分散値':sigma.tolist()})
# 実際の対戦をベースに得点の確率を推計
tmp1 = data_2018[['ホーム','アウェイ','home_team_score','away_team_score']]
Y1 = []
Y2 = []
for a in tmp1.values :
home = result_tbl2[result_tbl2['team_name']==a[0]]
away = result_tbl2[result_tbl2['team_name']==a[1]]
tmp = home['攻撃力'].values[0] + home['ホームアドバンテージ'].values[0] - away['守備力'].values[0]
home_score_para = np.exp(tmp)
tmp = away['攻撃力'].values[0] - home['ホームアドバンテージ'].values[0] - home['守備力'].values[0]
away_score_para = np.exp(tmp)
Y1.append(stats.poisson.pmf(np.arange(8),mu=home_score_para))
Y2.append(stats.poisson.pmf(np.arange(8),mu=away_score_para))
♯ 観測値と乗算して正解に割当てられた確率を抽出。エントロピー誤差を計算する場合は、これを対数に変換する
res = pd.get_dummies(tmp1['home_team_score']).values * Y1
print(np.mean(np.sum(res,axis=1)))
res = pd.get_dummies(tmp1['away_team_score']).values * Y2
print(np.mean(np.sum(res,axis=1)))
結果は、0.261と0.284ということで、予測対象が8として場合に一様に確率を割り当てると12.5%ですからそれなりといえそうです。つまり、予測の方向性はそれほどおかしいものではないと言えそうです。
なお、Stanを使うと推計対象パラメータ(攻撃力など)のサンプリング結果を入手できます。つまり、これらのパラメータは確定的なものではなく、何らかの確率的ゆらぎを持つものとして表現されます。
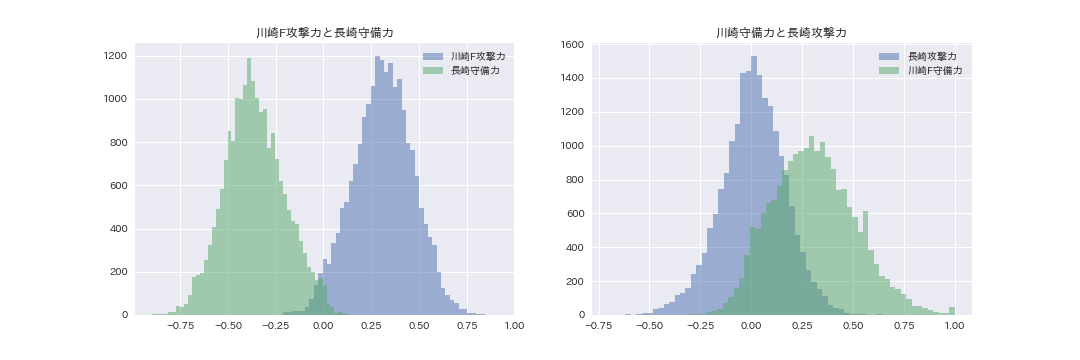
ケーススタディとして先と同様に川崎Fと長崎について分布を可視化します。
川崎Fと長崎の攻撃力・守備力ともに一定のバラつきを持っています。この標準偏差はsammaryメソッドで取り出すことができますが、実際のサンプリング結果がこのグラフです。得点は攻撃力と守備力の差異を使っているので、確率的にいうと、分布の重なった部分は両チームの攻撃力と守備力の大小関係が逆転する可能性を示しています。したがって、長崎の守備力が川崎Fの攻撃力を上回ることはめったになく、無失点で終わったとすれば、かなり偶然的なものといえそうです。一方、長崎の攻撃力が川崎Fの守備力を上回ることはそれなりにある(scipy.stats.poisson.sfをつかって川崎Fが平均的な守備力を発揮した場合に長崎の攻撃力が上回る確率を計算したところ10%程度となった)ということを示しています。したがって、長崎が得点したとしても単なる偶然とは言い切れないということになります。
上記の考察からいうと、先のスコア予測は各チームの通年を通した力から推計されたもので、実際の対戦当日の力を反映したものとはいえないことを意味しています。実際に主力選手のケガや累積警告による欠場や対戦相手の弱点を巧みについた戦術、さらにはチームの好不調の波、などによりチーム力が変動することは十分に起こります。つまり、実際の対戦当日の両チームのパラメータをスターティングメンバや各種スタッツを使って先の分布のどのあたりになるのかを推計することができれば、より精度を高めることができると思われます。ームの得点とアウェイチームの得点が独立して発生すると仮定すると、先の得点別確率分布のグラフ作成に使用したベクトルを掛け合わせて、マトリックスを生成すればいいことになります。
実際に川崎Fと長崎を事例に計算結果をヒートマップ化してみます。『川崎F 1-0 長崎』が14%と予測されるなど、期待したアウトプットの形式になりました。
まとめ
今回の報告はここまでとします。統計モデルを用いることでスコアとその発生確率を出力する予測モデルが実現できました。また、その予測の要因について、未知の変数である「攻撃力」や「守備力」を数値化することで、勝敗のキーポイントをうまく表現できることもわかります。
一方、まだモデルの改良点があることもわかります。まず、予測精度の向上の余地がまだあります。2018年のスコアからすると、0~3点の範囲にうまく分布するようなモデルに工夫する必要があると思います。また、今回のモデルは2018年のデータを使ってモデルを構築し、2018年の数値を使って性能を評価したに過ぎません。本来必要なモデルは未知のデータに対する高い予測性能を持つ予測モデルです。だからといって、2017年のデータで構築したモデルで2018年にあてはめたとしてうまくいく気もせず、このあたりの対応を考える必要があります。
今後、いくつかのアイデアを実験室、ある程度まとまったら投稿したいと思います。