LoginSignup
7
7

More than 3 years have passed since last update.

@ryouta0506(良太 重盛)

スポーツを機械学習する ～ Jリーグを事例にした分析 ～②

Posted at

　だいぶ期間があいてしまいましたが、以下の投稿の続きを報告したいと思います。
https://qiita.com/ryouta0506/items/100a2b252fbaeb73f493

　続きといっても、使用するモデルを変えてみようというものです。
　前回の報告では、得点はポアソン分布に従うと仮定しました。結果は、予測得点が０点・１点に集中して２点と予測するケースがほとんどありませんでした。サッカーにおいて３点より多いことは希少なので予測できなくても仕方がないと割り切れるのですが、やはり２～３点は相応の割合で予測できていないとうまくありません。そこで、他の確率分布を試したいと思います。

負の二項分布を使用

　ポアソン分布は、その定義上、期待値=分散をいう関係にあります。これは、期待値が小さいとバラつきも小さくなり、大きくなると大きくなるということを意味します。サッカーの得点のように基本的に０点・１点あたりに集中している場合、期待値が０点近くになるので、結果としてバラつきも小さくなるので２点・３点の出現確率が小さくなってしまいます。そこで、ポアソン分布の特性を持ちつつ分散をより一般化した統計モデルである負の二項分布を使用することにします。
　負の二項分布は、二項分布の親戚筋にあたる確率分布です。二項分布は、イベントの出現確率（例えば、コイントスで表が出る確率が0.5）が与えれている条件下で所定の試行回数（例えば10回）においてイベントが出現する回数の分布です。一方、負の二項分布は、イベントの出現確率とイベントの出現回数を所与とした試行回数の分布です。（注 実際にはこれ以外の定義もあるそうです。ここでは一番わかりやすいものにしました。）実際の統計モデリングの分野では、ポアソン分布の一般化（つまり、期待値=分散という制約条件を外した）したものとして扱われることが多いということなので、今回のモデルにも適用します。

　stanのコードは以下です。

model_code = """
data {
    int N;  // N Games
    int K;  // K Teams
    int home_team[N]; // Home Team ID
    int away_team[N]; // Away Team ID
    int ht_score[N] ; // Home Team score 
    int at_score[N] ; // Away Team score
}

parameters {
    real<lower=-1,upper=1> atk[K]; // atack
    real<lower=-1,upper=1> def[K]; // defence
    real<lower=0> home_adv[K];     // home advantage
    real<lower=0> sigma[K];        // sigma 
    real<lower=0> hadv_sigma;      // sigma home_advantage
    real<lower=0> phi[K] ;            // 
}

model {
    real param1 ;
    real param2 ;

    for (k in 1:K) {
        atk[k] ~ normal(0, sigma[k]);
        def[k] ~ normal(0, sigma[k]);
        home_adv[k] ~ normal(0, hadv_sigma);
        phi[k] ~ normal(0,10);
    }

    for (n in 1:N) {
        param1 = exp(home_adv[home_team[n]] + atk[home_team[n]] - def[away_team[n]]) ;
        param2 = exp((atk[away_team[n]]) - (def[home_team[n]] + home_adv[home_team[n]])) ;

        ht_score[n] ~ neg_binomial_2(param1,phi[home_team[n]]) ;
        at_score[n] ~ neg_binomial_2(param2,phi[away_team[n]]) ;

    }

}

generated quantities {
    int ht_predict[N] ;
    int at_predict[N] ;

    for (i in 1:N) {
        ht_predict[i] = neg_binomial_2_rng(exp(home_adv[home_team[i]] + atk[home_team[i]] - def[away_team[i]]),
                                                phi[home_team[i]]) ;
        at_predict[i] = neg_binomial_2_rng(exp((atk[away_team[i]]) - (def[home_team[i]] + home_adv[home_team[i]])),
                                                phi[away_team[i]]) ;
    }
}

"""

　stanで負の二項分布を表現する関数はneg_binomial_2()です。実際にはこれと別の関数もありますが、適用するパラメータによって使い分けることになります。実際の関数形に沿ったパラメータを設定する場合はneg_binomialを使ったほうがいいでしょう。ここでは、ポアソン分布の際にparam1およびparam2を平均とするモデルとしていたこともあり、平均と分散を引数として用いるneg_binomial_2を用いています。
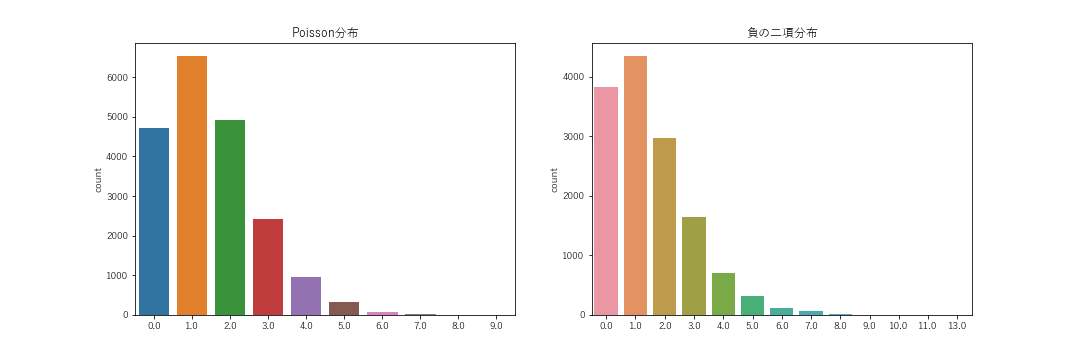
　参考までに川崎F対鹿島（ホーム 鹿島）の川崎側の得点の分布を示します。

fig02_negbinom_dist.png

　この試合において川崎Ｆは４得点していますので、理想は３点または４点の確率が最大になることです。ポアソン分布・負の二項分布ともに１点の確率が最大です。しかしながら、負の二項分布は０点および１点の確率が低減し、その分が２点以上に割り当てられています。そのため、この試合の４点という結果はポアソン分布よりも負の二項分布のほうが高い可能性があったことを表現できているといえます。
　上記は、川崎Ｆ対鹿島という特定の試合のケーススタディです。そこで、全体を通じてポアソン分布のモデルと負の二項分布のモデルとどちらが現実をうまく表現できているのかを尤度を使って検証します。

尤度によるモデル評価

　尤度とは、特定の確率分布のもとで手元にあるデータがその確率分布から出現する確率を表したものです。この尤度は、確率分布が正しいという仮定のもとであれば、手元にあるデータの出現する確率ということになりますが、手元にあるデータが正しいとすると推計した統計モデルの確からしさを表す指標ということになります。そこで、これを活用してモデルの評価をしたいと思います。
　今回の場合、手元のデータ（全306試合）が同時に成立する確率ということになりますので、個々の尤度を乗算した結果が全体の尤度ということになります。ただ、乗算では計算がうまくないので対数変換して合計することで手元データ全体の尤度を計算することにします。

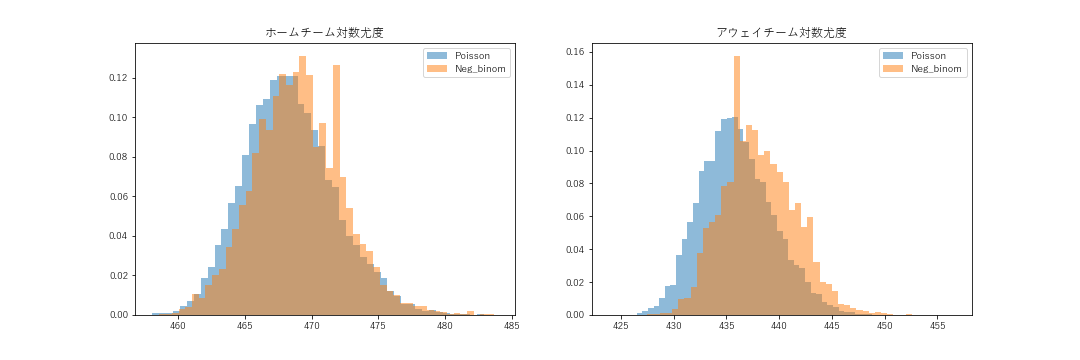
fig03_log_likehood.png

　上記はStanを使って推計した対数尤度の分布です。本来、対数尤度は負の値をとりますが、マイナスして値が大きいほど性能がよいことを意味するようにしています。つまり、ホームチーム・アウェイチームともに負の二項分布のほうが、観測値をうまく表現する確率分布となっていることを示しています。
　なお、尤度のstanによる計算は、generated quantities部に以下をコードを追記することで分布として取得できます。

ポアソン分布の尤度算定
    real ht_log_likehood ;
    real at_log_likehood ;

    ht_log_likehood = 0;
    at_log_likehood = 0;

    for (i in 1:N) {
        ht_log_likehood = ht_log_likehood + 
                          poisson_lpmf(ht_score[i] | exp((home_adv[home_team[i]] + atk[home_team[i]]) - (def[away_team[i]])));
        at_log_likehood = at_log_likehood +
                          poisson_lpmf(at_score[i] | exp((atk[away_team[i]]) - (def[home_team[i]] + home_adv[home_team[i]])));

    }
負の二項分布の尤度算定

    real ht_log_likehood ;
    real at_log_likehood ;

    ht_log_likehood = 0;
    at_log_likehood = 0;

    for (i in 1:N) {

        ht_log_likehood = ht_log_likehood +
                            neg_binomial_2_lpmf(ht_score[i] | 
                                exp(home_adv[home_team[i]] + atk[home_team[i]] - def[away_team[i]]),phi[home_team[i]]) ;

        at_log_likehood = at_log_likehood +
                            neg_binomial_2_lpmf(at_score[i] |
                                exp((atk[away_team[i]]) - (def[home_team[i]] + home_adv[home_team[i]])),phi[away_team[i]]) ;

    }

ゼロ過剰ポアソン分布

　これまでのモデルの場合、ひとつのモデルのもとで得点が決定されることを仮定してきました。しかしながら、ゼロ点という結果は、得点が入るケースとは異なる生成プロセスであるという仮定も成り立つと考えられます。例えば、試合を通して得点のチャンスの有無という分布があって、チャンスありの場合のみポアソン分布に従うというプロセスも考えられます。この場合、ゼロ点という結果は単純にポアソン分布にのみしたがって出現するわけではありません。むしろ、ベルヌーイ分布（チャンス有無を決定する分布）の影響を受けてポアソン分布よりもゼロ点の出現する割合が大きくなります。
　このようにポアソン分布従いつつゼロの出現確率を本来のものより大きくするようなモデルをゼロ過剰ポアソン分布があります。ここではこれを少しカスタマイズしたモデルを適用します。　
　実際のコードは以下の通りです。

model_code = """
data {
    int N;  // N Games
    int K;  // K Teams
    int home_team[N]; // Home Team ID
    int away_team[N]; // Away Team ID
    int ht_score[N] ; // Home Team score 
    int at_score[N] ; // Away Team score
}

transformed data {
    int ht_score_over_zero[N] ;
    int ht_score_trans[N]     ;
    int at_score_over_zero[N] ;
    int at_score_trans[N]     ;

    for (i in 1:N) {
        if (ht_score[i]>0) { 
            ht_score_over_zero[i] = 1 ;
            ht_score_trans[i] = ht_score[i]-1 ;
            }
        else {
            ht_score_over_zero[i] = 0 ;
            ht_score_trans[i] = 0 ;
            }

        if (at_score[i]>0) { 
            at_score_over_zero[i] = 1 ;
            at_score_trans[i] =at_score[i]-1 ;
            }
        else {
            at_score_over_zero[i] = 0 ;
            at_score_trans[i] = 0;
            }
    }
}

parameters {
    real<lower=-1,upper=1> atk[K]; // atack
    real<lower=-1,upper=1> def[K]; // defence
    real<lower=0> home_adv[K];     // home advantage
    real<lower=0> sigma[K];        // sigma 
    real<lower=0> hadv_sigma;      // sigma home_advantage

}

model {
    real param1 ;
    real param2 ;

    for (k in 1:K) {
        atk[k] ~ normal(0, sigma[k]);
        def[k] ~ normal(0, sigma[k]);
        home_adv[k] ~ normal(0, hadv_sigma);
    }

    for (n in 1:N) {
        param1 = home_adv[home_team[n]] + atk[home_team[n]] - def[away_team[n]] ;
        param2 = atk[away_team[n]] - (def[home_team[n]] + home_adv[home_team[n]]) ;

        ht_score_over_zero[n] ~ bernoulli(inv_logit(param1)) ;
        at_score_over_zero[n] ~ bernoulli(inv_logit(param2)) ;

        if (ht_score_over_zero[n] >0 ) 
            ht_score_trans[n] ~ poisson(exp(param1));

            at_score_trans[n] ~ poisson(exp(param2));
    }

}

generated quantities {
    int ht_predict_score[N] ;
    int at_predict_score[N] ;
    real ht_log_likehood ;
    real at_log_likehood ;

    ht_log_likehood = 0 ;
    at_log_likehood = 0 ;

    for (i in 1:N) {
        ht_log_likehood = ht_log_likehood + 
                            bernoulli_lpmf(ht_score_over_zero[i]|
                                                inv_logit(home_adv[home_team[i]] + atk[home_team[i]] - def[away_team[i]])) ;
        at_log_likehood = at_log_likehood +
                            bernoulli_lpmf(at_score_over_zero[i]|
                                                inv_logit(atk[away_team[i]] - (def[home_team[i]] + home_adv[home_team[i]]))) ;

        if (ht_score_over_zero[i]>0) {
            ht_log_likehood = ht_log_likehood +
                            poisson_lpmf(ht_score_trans[i]|
                                                exp(home_adv[home_team[i]] + atk[home_team[i]] - def[away_team[i]])) ;
        }
        if (at_score_over_zero[i]>0) {
            at_log_likehood = at_log_likehood +
                            poisson_lpmf(at_score_trans[i]|
                                                exp(atk[away_team[i]] - (def[home_team[i]] + home_adv[home_team[i]]))) ;
        }
    }
}



        if (bernoulli_rng(inv_logit(home_adv[home_team[i]] + atk[home_team[i]] - def[away_team[i]]))==0) {
            ht_predict_score[i] = 0 ;
        }
        else {
            ht_predict_score[i] = poisson_rng(exp(home_adv[home_team[i]] + atk[home_team[i]] - def[away_team[i]])) +1 ;
        }

        if (bernoulli_rng(inv_logit(home_adv[home_team[i]] + atk[home_team[i]] - def[away_team[i]]))==0) {
            at_predict_score[i] = 0;
        }
        else {
            at_predict_score[i] = poisson_rng(exp(atk[away_team[i]] - def[home_team[i]] + home_adv[home_team[i]])) +1 ;
        }

"""

　今回のモデルの基本構造は、「得点できる」と「得点できない」のベルヌーイ分布と得点できる場合のポアソン分布の混合とします。
　このうち、ベルヌーイ分布については、攻撃力・守備力・ホームアドバンテージから計算した結果をsigmoid関数（logit関数の逆関数）を使って確率に変換したものを用いています。このモデルによって「得点できない」と判定された場合はゼロ固定とします。「得点できる」と判定された場合、ポアソン分布を用います。本来のポアソン分布はゼロ点の可能性が程度の差はあるものの存在します。しかしながら、今回のポアソン分布を適用するケースは「得点できる」なので、ゼロ点が出現することは矛盾してしまいます。そこで、ポアソン分布を右へ1.0シフトすることでゼロ点が出現しないようにします。
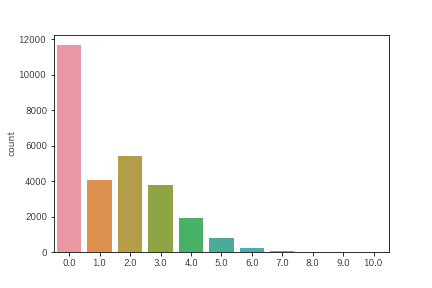
　まず、川崎F対鹿島（ホーム 鹿島）の川崎側の得点の分布を確認します。

fig04_ZIP.png

　0点の割合が最も大きくなっていますが、これは得点できたか・できなかったのかを表したものです。この0点の割合は41.8%となったので、この試合は川崎Ｆが得点できたと考えたほうが良いようです。そうとすると、この試合は川崎Ｆが２点取ると見込むべきだということになります。これはポアソン分布・負の二項分布の１点と見込まれることと比較するとかなりいい結果のように思われます。加えていうと、このモデルの場合、川崎Ｆが４得点するケースが11.9％と結構大きいことになります。

　最後にこのモデルの尤度を確認します。
　本モデルの場合、尤度はベルヌーイ分布とポアソン分布を同時に満たすケースなので各々の尤度の乗算ということになります。よってこれを対数変換すると、ベルヌーイ分布の対数尤度とポアソン分布の対数尤度の加算で計算できることになります。
　上記をstanのコードにすると以下のようになります。

generated quantities {

    real ht_log_likehood ;
    real at_log_likehood ;

    ht_log_likehood = 0 ;
    at_log_likehood = 0 ;

    for (i in 1:N) {
        ht_log_likehood = ht_log_likehood + 
                            bernoulli_lpmf(ht_score_over_zero[i]|
                                                inv_logit(home_adv[home_team[i]] + atk[home_team[i]] - def[away_team[i]])) ;
        at_log_likehood = at_log_likehood +
                            bernoulli_lpmf(at_score_over_zero[i]|
                                                inv_logit(atk[away_team[i]] - (def[home_team[i]] + home_adv[home_team[i]]))) ;

        if (ht_score_over_zero[i]>0) {
            ht_log_likehood = ht_log_likehood +
                            poisson_lpmf(ht_score_trans[i]|
                                                exp(home_adv[home_team[i]] + atk[home_team[i]] - def[away_team[i]])) ;
        }
        if (at_score_over_zero[i]>0) {
            at_log_likehood = at_log_likehood +
                            poisson_lpmf(at_score_trans[i]|
                                                exp(atk[away_team[i]] - (def[home_team[i]] + home_adv[home_team[i]]))) ;
        }                                  
    }
}

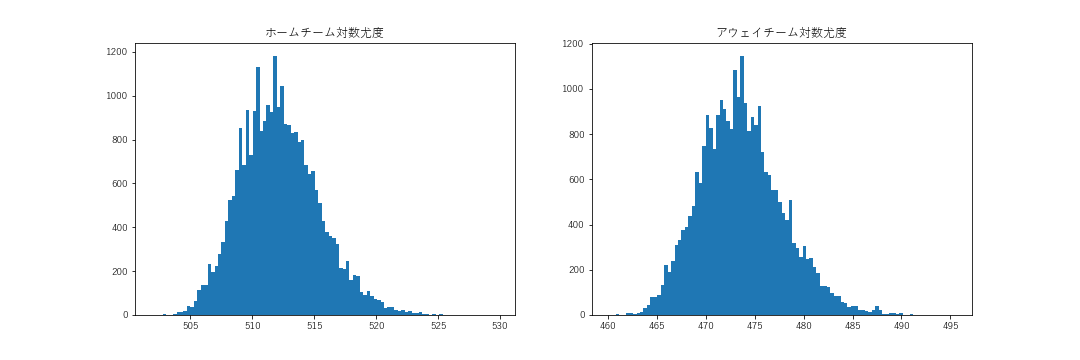
　結果は以下のようになりました。全体としての尤度は、負の二項分布よりも大きくなり、このモデルが最も観測値をうまく表現していることがわかりました。

fig05_ZIP_loglikehood.png

まとめ

　サッカーの得点の予測には、ゼロ過剰ポアソン分布が最も観測値をうまく表現できることがわかりました。これにより各チームの攻撃力・守備力を定義できることになります。攻撃力・守備力は、レギュラーメンバおよびその特性（走力など）といったもので決定されるものです。
　よって、今後はこの関係性をうまくモデル化することができれば、チーム特性→攻撃力・守備力→得点という順序で得点を予測できると考えます。

7
7
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
7
7