はじめに
機械学習で,回帰や分類,SVMなどの予測値は,「XXX以上とそれ以下」や「YYYの範囲の中と外」というように比較的単純なもので,XOR回路のような判定をさせようとすると難しくなってくる.
人工ニューラルネットワーク
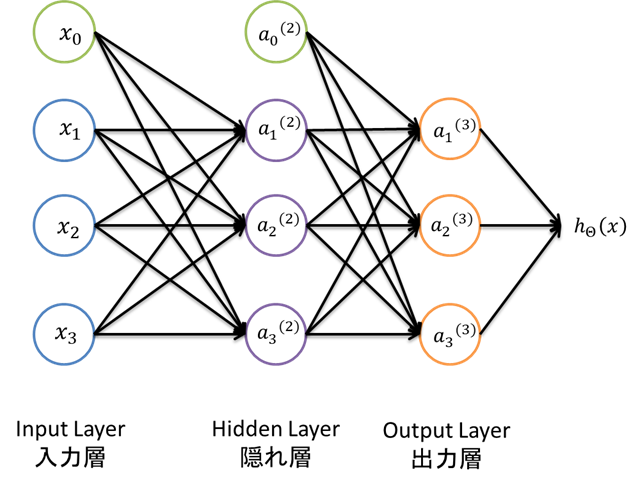
機械学習におけるニューラルネットワークと呼ばれるものは厳密には,人口ニューラルネットワーク(Artificial Neural Network: ANN)という.ANNは,複数の入力値に対して出力値を算出するモデルの一種で,脳細胞を模したニューロンモデルを用いて,層状に連結させたものを指す.この層の数が少ないものを単なるニューラルネットワーク(Shallow-layer Neural Network)と,多いものを深層ニューラルネットワーク(Deep-layer Neural Network: DNN)と名前を付け呼び分けていたりする.
ニューロンモデル
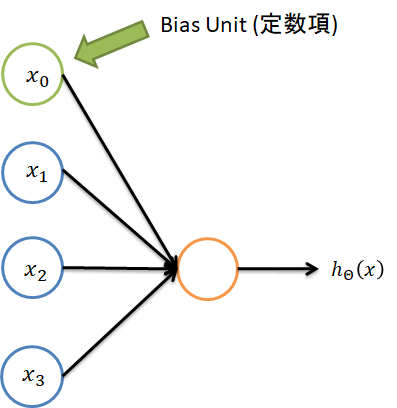
上図では3つの入力値に対して1つの出力値を求めるニューロンモデルである.$x_0$はバイアス項となっていて,入力値は常に1となっている.
真ん中の円がそれに当たる.この時の計算方法は,
\begin{align}
z &= \sum_{i=0}^{3}\theta_ix_i \\
h_{\Theta}(x) &= g(z) \\
\end{align}
というようになる.$z$はニューロンに対する入力値の重みつき総和になっている.そして,出力値は活性化関数と呼ばれるものを通過させる.
今回の式でいうところの$g(\cdot)$である.活性化関数は,ReLU(Rectified Linear Unit)やSigmoid関数,tanh関数などを用いる.
演算量が多いDNNでは,収束速度の速いReLUを用いることが多い.また,DNNでは,1つの円をグラフ理論などでよく使われるノード(Node)と呼ぶ.
この図は,3層構造のANNとなっている.
入力層と出力層の間にある層を隠れ層と呼び,外部から見えないような感じになる.
このモデルでは,出力値は3つになるため,分類モデルとなっている.
計算方法
3層ANNの計算についてみていくことにする.
隠れ層の1つ目の計算をしてみる.
\begin{align}
z_{1}^{(2)} &= \sum_{i=0}^{3}\theta_ix_i \\
a_{1}^{(2)} &= g(z_{1}^{(2)}) \\
\end{align}
この計算を$a_{2}{(2)}$と$a_{3}{(2)}$も同じようにできる.
これをベクトル化させて一気に計算してみる.まず,
\begin{align}
a^{(1)} &= \left(
\begin{matrix}
1\\
x_1\\
x_2\\
x_3\\
\end{matrix}
\right)\\
\\
\Theta^{(1)} &= \left(
\begin{matrix}
\theta_{01} & \theta_{11} & \theta_{21} & \theta_{31} \\
\theta_{02} & \theta_{12} & \theta_{22} & \theta_{32} \\
\theta_{03} & \theta_{13} & \theta_{23} & \theta_{33} \\
\end{matrix}\right)
\end{align}
と入力値のベクトル$a^{(1)}$とパラメータの行列$\Theta^{(1)}$を用意する.これらを使って,
\begin{align}
z^{(2)} &= \Theta^{(1)}a^{(1)} \\
a^{(2)} &= g(z^{(2)}) \\
\end{align}
というように整理することが出来る.ここでバイアス項を考慮させて,以下のように$a^{(2)}$を加工しておく.
a^{(2)} := \left(
\begin{matrix}
1 \\
a_1^{(2)} \\
a_2^{(2)} \\
a_3^{(2)} \\
\end{matrix}
\right)
そして,出力層の計算は以下のようになる.
\begin{align}
z^{(3)} &= \Theta^{(2)}a^{(2)} \\
a^{(3)} &= g(z^{(3)}) \\
h_{\Theta}(x) &= a^{(3)} \\
\end{align}
$h_{\Theta}(x)$は,3つのノードの出力値を集めたものなので,3次のベクトルとなってる.
学習方法
上記で,入力値$x$から出力値$h_{\Theta}(x)$を求めることが出来た.
これを次のように組み立てる.
\begin{align}
J(\Theta)=&-\frac{1}{m}\left[
\sum_{i=1}^m\sum_{k=1}^K y_k^{(i)} \log{h_{\theta}(x^{(i)})_k + (1-y_k^{(i)})\log(1-h_{\theta}(x^{(i)})_k)}
\right] \\
&+ \frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_l+1}(\Theta_{ji}^{(l)})^2
\end{align}
この大きな式がANNにおけるコスト関数となる.$J(\Theta)$の値が最小値になるような$\Theta$を探すことになる.
ここで,$m$は学習データ数,$K$は出力値の次元数(例のモデルだと3),$L$は層数,$s_l$は$l$層のノード数となっている.第1項の$\sum$の内側にある式は,分類の際に使用するロジスティック回帰である.そして,第2項は正則化項で,過学習(Over-fitting)を抑制し,バランスの良いパラメータを手に入れる効果がある.
ANNでも,勾配降下法による最適化問題を解くことになるが,$\frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)$を手に入れる必要がある.
この値を手に入れるのに,バックプロパゲーション法(Back Propagation Algorithm)を用いる.
ちなみに,上記で計算していたものを,その対としてForward Propagationと呼ぶこともある.
まとめ
今回は,ニューラルネットワークの計算方法についてまとめました.
通常の回帰モデルから一気に変数や添え字が増えるため,訳が分からないことがあります.
その時は,1つづつ砕いてゆっくりと進めていけば,問題ないでしょう.
Back Propagation Algorithmについては,別の機会に記事にしようと思います.